考虑道路实况的冷链物流多温共配路径优化研究
曹文彬 谢慧雯


摘 要:随着我国居民生活质量与消费水平的提高,居民对于生鲜冷链产品的需求正在不断攀升,考虑到冷链产品易腐的特性,为了减少产品损耗,提高消费者满意度,文章引入多温共配模式,同时考虑配送过程中道路实际状况的影响,构建了以总成本最低为目标的冷链配送路径优化模型。模型总成本包括车辆固定成本、车辆运输成本、制冷成本、碳排放成本。为求解所建模型,从启发式因子、移动概率的选择、信息素更新策略等多个方面对传统蚁群算法进行了改进,并混入了2-opt局部优化算法。最后,通过对照仿真实验,证实了模型及算法的有效性。
关键词:VRP;冷链物流;碳排放;道路实况;多温共配;蚁群算法
中图分类号:F252.14 文献标志码:A DOI:10.13714/j.cnki.1002-3100.2023.15.033
Abstract: Considering the perishable characteristics of cold chain products, in order to reduce product loss and improve consumer satisfaction, this paper introduces a multi-temperature distribution model and considers the influence of the actual road conditions in the distribution process, and constructs a cold chain distribution path optimization model with the lowest total cost as the goal. The total cost of the model includes vehicle fixed cost, vehicle transportation cost, refrigeration cost and carbon emission cost. To solve the proposed model, this paper improves the traditional ant colony algorithm from several aspects such as heuristic factors, selection of movement probability, pheromone update strategy, etc., and mixes in the 2-opt local optimization algorithm. Finally, the author confirms the effectiveness of the model and algorithm through controlled simulation experiments.
Key words: VRP; cold chain logistics; carbon emission; road reality; multi-temperature co-distribution; ant colony algorithm
0 引 言
近些年,随着我国居民消费水平和生活质量的提高,消费者的食品安全意识也在不断提升,居民对于生鲜冷链产品的需求正在快速增加,我国的冷链物流行业正处于快速发展阶段。冷链物流因冷链产品易腐的特殊性,对配送环境和配送方式要求较高,因此,在配送中如何降低损耗和配送成本,是行业内亟待解决的问题。目前,交通运输仍是全球第二大碳排放来源,约占全球总排放量的24%。而相较于普通公路运输,冷链物流因在运输和储存过程需要对产品进行冷藏,需要更大的能源消耗,这将进一步加剧全球温室效应,为此,冷链物流未来亦需要实现绿色化转型。
目前,国内外有关冷链物流车辆路径问题[1]的研究已取得一定成果。部分学者致力于冷链物流多温共配模式的研究,其中Kuo Ju Chia, Chen Mu Chen[2]指出对于温度敏感和易腐蚀的冷链产品,温度监测是有必要的,但实时监测成本过高,为此提出了一种多温联合配送的模式,以储存和运输有着不同温度需求的多种產品。Chaug-Ing Hsu等[3-5]对比了冷链产品多温共配模式的传统技术和新技术,实验结果表明多温共配能在有效降低运输成本的同时提高消费者满意度,提出可以考虑引入蓄冷保温箱来降低总成本。也有部分学者从碳排放的角度研究了冷链产品的多温共配问题,Wei-Ting Chen等[6]考虑了冷链产品运输产生的温室气体,构建了考虑气体排放和时间窗的多温共配VRP模型,实验结果证实了多温共配模式的环境友好性。杨建华等[7]使用碳税来刻画碳排放成本,构建了一个仓库能力有限的冷链物流配送模型,为企业提供了运营决策依据。潘茜茜、干宏程[8]在传统冷链物流配送路径问题研究中引入碳排放,使用考虑车辆载重的单位距离燃料消耗来刻画碳排放量,并以此计算碳排放成本。戴夏静、梁承姬[9]研究了带时间窗的蓄冷式多温共配冷链VRP问题,并利用遗传算法对问题进行求解,验证了蓄冷式在总体上优于机械式。李顺勇等[10]从实际交通一般存在多通路的视角出发,构建了考虑多通路的GVRP模型,考虑了实际配送途中车辆的多通路选择问题,研究结果显示在时变网络下的多通路VRP能更好地降低油耗。张济风、杨中华[11]考虑到配送途中不同路段车辆具有不同行驶速度,基于时变网络的角度构建了冷链物流多温共配VRP模型,使用模拟退火算法进行求解,对货损成本中的腐败函数进行改进,刻画了一种随时间动态变化的腐败函数。
综上所述,现有车辆路径优化问题在多个研究方向均有研究成果,但从碳排放问题、配送模式和道路实况等多个角度综合考虑的研究较少。为此,本文考虑到冷链产品易腐的特性,为降低产品损耗提高消费者满意度,采用蓄冷式冷藏车实现多温共配模式,同时考虑了配送过程中道路实况带来的影响,构建了带时间窗的冷链配送路径优化模型,求解冷链配送的最优路径,在满足消费者需求的基础上提高满意度、降低配送成本,并实现配送过程的低碳。
1 问题描述及模型构建
1.1 问题描述
本文研究的是低碳视角下考虑道路实况的冷链物流多温共配路径优化问题,此问题可以具体描述为一个冷链物流配送中心向多个客户配送冷链产品,配送中心采用多温共配模式,使用蓄冷式冷藏车进行配送,为客户提供三类不同温层货物,在考虑车辆装载限制和时间窗约束的前提下,满足客户需求,构建一个总成本最小化的冷链物流配送路径优化模型,并对该模型进行求解。
1.2 模型假设与约束
为了将问题抽象为数学模型,需要作如下一些假设与约束:(1)本文研究的是单一配送中心向多个客户点服务的路径优化问题;(2)车辆为蓄冷式冷藏车,最大装载量已知,且所有车辆型号相同;(3)车辆配送路线上的总客户需求,不能超过车辆最大装载量和体积,且蓄冷箱个数不能超过车辆蓄冷箱最大装载数量;(4)蓄冷箱的容量固定,且三个温层的温度设置固定;(5)每个客户只能使用一辆车进行服务;(6)所有客户的地理位置、需求量、时间窗要求已知;(7)所有车辆在配送任务完成后返回配送中心,配送途中不存在中途补货的情况;(8)多温共配模式下,能满足不同温层产品的温度需求,不考虑货损成本;(9)车辆的行驶速度受道路实际情况影响。
1.3 符号说明
本文模型中所涉及的符号说明如下:
(1)标 号
N:配送中心和客户点集合,Nn|n=0,1,2,…,N;N:客户点集合,Nn|n=1,2,…,
N;i, j:配送中心和客户点编号,i, j=0,1,2,…,n(0为配送中心);V:车辆集合,Vv|v=1,2,…,V;k:车辆编号,k=1,2,…,v;T:时间区间集合,Tt|t=1,2,…,T;h:时间区间编号,h=1,2,…,t;M:配送货物类别集合,M=1,2,3;m:货物类别编号,m∈M,m=1表示温层1,m=2表示温层2,m=3表示温层3。
(2)参 数
U:车辆额定载重;q:蓄冷箱最大容量;n:每辆车最多可装载的蓄冷箱数量;U:车辆自重;U:车辆k不同温层产品的装载量;U:车辆k离开客户i的载重量;U:车辆k离开客户i不同温层产品的剩余量;q:客户i不同温层产品的需求量;p:车辆k装载不同温层产品的蓄冷箱使用数量;d:客户点i,j之间的距离;v:在h时间区间,车辆在路径i, j的行驶速度;t:车辆k从配送中心出发的时间;t:车辆k到达i客户的时间;t:用户i的服务时间;c:不同温层的蓄冷箱的蓄冷成本;C:单位距离燃油消耗成本。
(3)变 量
x:路径i, j是否被访问,1=是,0=否;y:路径i, j是否被车辆k访问,1=是,0=否;z:在h时间区间,路径i, j是否被车辆k访问,1=是,0=否。
1.4 目标函数分析
本文所构建的数学模型旨在考虑配送中碳排放量的基础上,实现冷链物流配送阶段的成本最优。冷链物流实际配送成本受多方面因素影响,若以单一因素作为优化目标,不能良好的刻画现实情况,因此,本文模型以综合成本最低为目标,目标函数主要包括:车辆的固定成本、运输成本、制冷成本、碳排放成本。
(1)车辆固定成本
车辆的固定成本一般为常数,一般包括车辆的折舊费、维修费用及驾驶员工资等,与车辆的行驶距离和客户的数量无关。若单车的固定成本为f, 则运输过程中的车辆固定成本C可以用公式(1)表示:
C=f (1)
(2)车辆运输成本
车辆的运输成本通常与车辆的行驶距离成正比,主要为车辆的燃油消耗成本,本模型的车辆运输成本C可以用公式(2)表示:
C=ydC (2)
(3)制冷成本
本模式使用蓄冷式冷藏车,在车辆未行驶阶段为蓄冷箱蓄冷储能,在车辆行驶过程中不使用动力源,因此,制冷成本与不同温层蓄冷箱的使用数量相关,本模型的制冷成本C可以用公式(3)表示:
C=cp (3)
(4)碳排放成本
本文采用蓄冷式冷藏车,制冷设备不产生碳排放,在运输途中车辆的碳排放量主要与车辆燃油消耗有关,行驶途中燃油消耗一般取决于车辆的行驶距离和装载量,制冷设备产生的碳排放一般与行驶距离有关,模型的碳排放成本C的计算相关公式如下:
C=pfydδ
U (4)
δX=a
U+X+b (5)
δ=aU+b (6)
δ=a
U+U+b (7)
δ
U=δ+U (8)
在式(4)中,p為单位碳税;f为碳排放系数;δ
U为单位距离的燃油消耗量。根据式(5)、式(6)、式(7)可以得到式(8);a和b为相关系数; δ为满载时的单位距离燃油消耗量,δ为空载时的单位距离的燃油消耗量。
1.5 模型建立
综上所述,本文构建的基于低碳视角下考虑道路实况的冷链物流多温共配路径优化模型如下:
Z=Min
f+
y
dC
+
c
p
+pf
y
d
fδ
U (9)
s.t.
x=y, ?i∈N, j∈N, i≠j (10)
y=1, ?j∈N (11)
y=1, ?i∈N (12)
y+y≤1, ?i∈N, j∈N, i≠j, k∈V (13)
y=y≤1, ?k∈V (14)
yq≤U, ?k∈V (15)
P≤n, ?k∈V (16)
t=z
t
+t
+, ?j∈N, i≠j, k∈V (17)
U=y
U
-q, j∈N, i≠j, k∈V, m∈M (18)
其中:式(9)为模型目标函数;式(10)至式(18)为模型约束条件;式(10)表示若路径i, j被访问,则一定有一辆车经过路径i, j;式(11)和式(12)表示一个客户只能被访问一次,且只由同一辆车服务;式(13)表示在配送过程中车辆只能从一个方向向另一方向行驶,不能回流;式(14)表示所有车辆只能从配送中心出发,且在完成配送后返回配送中心;式(15)表示车辆k所服务的所有客户总需求量不能超过车辆的额定载重;式(16)表示车辆k使用的蓄冷箱不能超过车辆最大的蓄冷箱装载量;式(17)表示车辆k到达客户j的时间等于到达客户i的时间与客户i的服务时间和车辆在路段i, j的行驶时间之和;式(18)表示车辆在服务完客户j后各温层货物的减少。
2 改进蚁群算法
蚁群算法效果的优劣主要取决于启发式因子,移动概率选择,信息素更新策略等相关参数的设置,因此,为提高算法效率和精度,需要在基础算法上对多个方面进行改进,使算法更加适合本文所研究的问题。
2.1 启发因子
启发式因子作为激励蚂蚁进行节点选择的关键因素,也是蚁群算法中最核心的组成部分之一,能够直接影响算法求解质量。传统蚁群算法中,一般使用距离来刻画启发式因子,本文为低碳视角下的冷链配送路径优化问题,而车辆碳排放与车辆载重相关,若仅以距离来刻画启发式因子会对求解结果产生影响,可能导致燃油浪费以及碳排放成本增加。为此,通过引入顾客对商品的需求量作为启发式因子,使算法选取下一个节点时充分考虑了燃油消耗这一影响因素。启发式因子如式(19)所示。
φ= (19)
2.2 移动概率的选择
蚂蚁将信息素和启发式信息结合起来,采用一种概率决策机制来选取下一个可移动的节点,并在蚂蚁构造完一个可行解之后对这种机制进行评价,进而确定更新信息素时信息素释放量。
为了避免算法失去随机性,引入轮盘赌选择策略,蚂蚁k在顾客i时选择顾客j的概率表示为p,如式(20)所示。
p= (20)
在式(20)中:φ表示路径i, j的自启发量,τ表示路径i, j的信息素值;α为信息素启发式因子,β为期望启发式因子,α和β是可调整参数,代表了信息素浓度和自启发量的重要程度;在开始时刻,设置各条路径的信息素浓度相同为τ(τ为常数)。
为了避免算法陷入停滞,采用随机性选择和确定性选择相结合的概率选择策略,蚂蚁k根据式(21)选择客户j。
j= (21)
在式(21)中,λ为一个在区间0,1的随机量,λ为一个已知常量。这种选擇策略表示,当蚂蚁需要寻找下一个节点时,会随机产生一个区间在0,1范围内的数,蚂蚁将根据这个随机数的大小按公式(21)决定蚂蚁向哪个节点移动。
2.3 信息素更新策略
在传统算法中,在一代的所有蚂蚁完成路径构造后,将对所有蚂蚁经过的路径增加信息素,此时信息素的更新没有对优解和劣解进行区分,使算法效率降低且容易导致局部最优。在本文中,在所有蚂蚁构造完路径后,只有找到最优路径的蚂蚁可以在其经过的路径上增加信息素。信息素更新方法如式(22)所示,其中:Δτ=Q/L,Q为常数,L为该路径的长度,ρ为信息素的挥发系数。
τ=1-ρτ+Δτ (22)
同時,为了避免某条路径上的信息素浓度过高,导致算法过早收敛,对所有路径的信息素值设置上限和下限,分别为τ,τ。
2.4 局部优化
当所有蚂蚁都完成路径的构造后,且信息素未更新之前,引入2-opt算法对每一代的最优解进行局部优化,以达到算法收敛速度加快的目的,从而提高算法的运行效率。
2.5 算法步骤
本文改进蚁群算法的求解步骤如下:
步骤1:初始化参数α, β, ρ, Q;设置迭代次数Nc=0,τ=τ;蚂蚁数量为m,顾客数量为n。
步骤2:将起点置于当前解集中,判断未经过的节点是否满足时间窗、车辆载重及蓄冷箱约束,若满足,则根据式(21)来选择下一节点j,将蚂蚁k移动到j,且将j置于当前解集中。
步骤3:当所有节点都置于解集中,判断k是否等于m,若等于,则转步骤4;否则,k=k+1,转步骤2。
步骤4:记录各蚂蚁的目标函数值,找到其中的最优解。
步骤5:应用2-opt算法对最优路径进行局部优化。
步骤6:对最优路径进行信息素更新τ=1-ρτ+Δτ,对其他路径进行信息素更新τ=1-ρτ。
步骤7:Nc=Nc+1。
步骤8:判断Nc是否达到最大迭代次数,若达到。则停止搜素,输出结果;否则,清空禁忌表,转步骤2。
3 仿真分析
本文以无锡市某家冷链物流配送公司作为算例对象,该公司为某社区团购平台提供冷链配送服务。该社区团购平台在无锡设置了前置仓,本文以其中一家生鲜冷链仓库作为配送中心,同时选取了无锡市内25个社区作为客户点,各客户的地理位置、各温层货物需求量均已知,如表1所示。由于该社区团购平台规定前一日及当日10:00前的订单,客户可在当日16:00后于该平台自提点提货,且考虑到仓库需对货物进行分拣,所以各客户点的配送服务时间窗为当日11:00—16:00。根据百度地图交通出行大数据平台提供的交通拥堵指数数据,本文以1h划分时段计算了无锡市内每个时段的平均交通拥堵指数,如表2所示,且无锡市内车辆正常通行速度为50km/h。
本文使用单一车型进行配送,该蓄冷式冷藏车的最大装载量为2.5t,蓄冷箱的最大装载量为100kg,冷藏车可容纳的蓄冷箱个数为22个。蓄冷箱可设置三个温层,温层1为10℃~0℃,温层2为0℃~-10°℃,温层3为-10℃~-20℃,其他参数设置如表3所示。
3.1 模型求解
使用上文所提供的配送信息,对低碳视角下考虑道路实况的冷链物流多温共配模型进行求解10次,其中成本最优的路径安排如表4所示。
由表4计算可知,为服务25个客户配送中心需要派出三辆冷藏车;配送过程中车辆行驶总距离为202.965km;总成本为
1 896.242 7元,其中固定成本为750元,运输成本为608.895 1元,制冷成本为468元,碳排放成本为69.347 7元。车辆的配送路径如图1所示。
3.2 多车型配送模式的实验结果
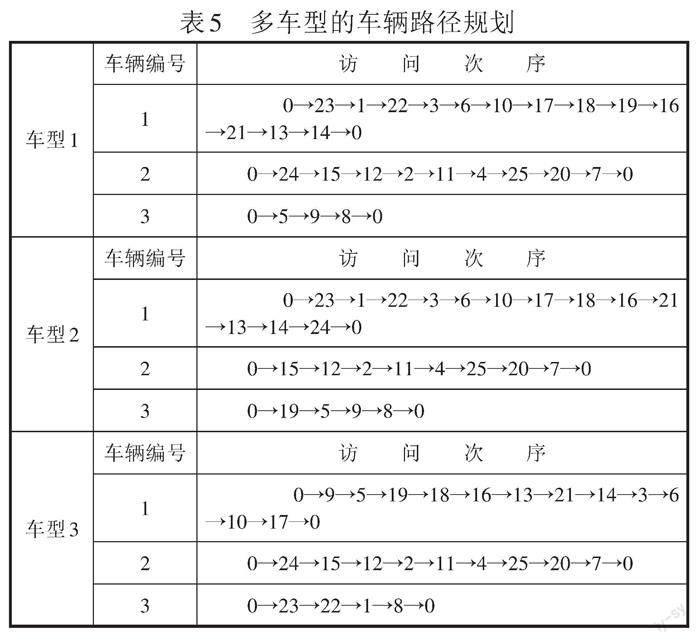
采用传统的多车型冷链配送模式,使用满足三种不同温层的三种冷藏车进行配送,在10次运行结果中,成本最优的路径规划如表5所示。
该配送方案的行驶总距离为599.040 5km总成本为3 426.394元,固定成本为1 125元,运输成本为1 198.081 1元,制冷成本为928.703元,碳排放成本为174.609 7元。与上文中考虑道路实况的冷链多温共配模型路径优化结果对比,可以发现多车型模式的成本较高,其总成本增加了约80%,其中固定成本增加了50%,运输成本增加了约97%,制冷成本增加了约98%,碳排放成本增加了约152%。由此,可以得出相较于传统的多车型冷链配送模式,多温共配模式的应用可以有效的降低配送成本,提高车辆的装载量,提升配送过程的绿色度。
4 结 论
本文从实际情况出发,综合考虑配送车辆的固定成本、运输成本、制冷成本,以及配送过程中产生的碳排放成本和因未满足客户要求的服务时间窗而产生的惩罚成本作为目标函数,并结合配送过程中的道路实况,引入多温共配模式构建冷链物流的路径优化模型,为解决该问题本文提出了一种结合2-opt局部搜索机制改进的蚁群算法。实验结果证实了算法的有效性并表明在冷链物流配送中,引入多温共配模式,同时考虑道路实况所带来的影响,能有效降低冷链物流配送成本,提升冷链物流配送过程的绿色水平。
参考文献:
[1] MARIUS M SOLOMON, JACQUES DESROSIERS. Time window constrained routing and scheduling problems[J]. Transportation Science, 1988,22(1):1-13.
[2] KUO JU CHIA, CHEN MU CHEN. Developing an advanced multi-temperature joint distribution system for the food cold chain[J]. Food Control, 2010,21(4):559-566.
[3] CHAUG-ING HSU, KANG-PO LIU. A model for facilities planning for multi-temperature joint distribution system[J]. Elsevier, 2011,22(12):1873-1882.
[4] CHAUG-ING HSU, WEI-TING CHEN. Optimizing fleet size and delivery scheduling for multi-temperature food distribution[J]. Applied Mathematical Modelling, 2014,38(3):1077-1091.
[5] HSU CHAUG ING, CHEN WEI TING, WU WEI JEN. Optimal delivery cycles for joint distribution of multi-temperature food[J]. Food Control, 2013,34(1):106-114.
[6] WEI-TING CHEN, CHAUG-ING HSU. Greenhouse gas emission estimation for temperature-controlled food distribution systems[J]. Journal of Cleaner Production, 2015,104:139-147.
[7] 楊建华,郭继东,马书刚. 碳税约束的城市冷链物流配送网络设计[J]. 工业工程,2012,15(5):86-91.
[8] 潘茜茜,干宏程. 考虑碳排放的冷链物流配送路径优化研究[J]. 数学的实践与认识,2016,46(2):62-68.
[9] 戴夏静,梁承姬. 带时间窗的蓄冷式多温共配冷链配送问题研究[J]. 重庆师范大学学报(自然科学版),2017,34(5):18-25.
[10] 李顺勇,但斌,葛显龙. 多通路时变网络下低碳车辆路径优化模型与算法[J]. 计算机集成制造系统,2019,25(2):454-468.
[11] 张济风,杨中华. 时变路网环境下多温冷链配送路径优化研究[J]. 重庆师范大学学报(自然科学版),2020,37(1):119-126.
收稿日期:2022-10-25
作者简介:曹文彬(1967—),男,江苏泰兴人,江南大学商学院,副教授,博士,研究方向:物流技术经济与管理;谢慧雯(1998—),女,江西赣州人,江南大学商学院物流工程硕士研究生,研究方向:供应链管理。
引文格式:曹文彬,谢慧雯. 考虑道路实况的冷链物流多温共配路径优化研究[J]. 物流科技,2023,46(15):138-143.

