相邻结构间设置黏弹性阻尼器的风荷载响应分析

杨雪峰 李创第 李宇翔 葛新广

摘 要：在两相邻结构间设置黏弹性阻尼器能够有效降低结构在风荷载下的动力响应。选取广义Maxwell模型为黏弹性阻尼器计算模型，提出了一种相邻结构间设置黏弹性阻尼器的耗能减振结构风振响应的解析解法。首先，根据广义Maxwell黏弹性阻尼器构造图推导出微分型本构关系，并将其与两相邻结构的运动方程组进行耦合；其次，运用复模态法将相邻结构的响应（位移、速度、层间位移和层间速度）表示为一阶线性方程组合，并基于虚拟激励法获得上述响应的统一形式的频域解；然后，基于频响函数二次分解法，获得了基于Davenport的风速谱，并考虑空间相关性结构响应方差的解析解；最后，通过算例与虚拟激励法计算结果对比验证了所提方法的正确性，并分析了阻尼器在相邻结构风振控制中的减振效果。

关键词：相邻结构；广义Maxwell黏弹性阻尼器；Davenport风速谱；频响函数二次分解法；减振效果

中图分类号：TU311.3；TU318 DOI：10.16375/j.cnki.cn45-1395/t.2023.03.008

0 引言

由于城市化的发展和土地资源的紧缺，建筑物之间的距离越来越狭窄，许多建筑物设计成大底盘多塔结构或者连廊结构而形成相邻结构，在强风或强震的作用下容易引起相邻建筑物碰撞[1-3]。相邻建筑结构间可安装阻尼器，来耗散部分风荷载或地震产生的能量，以降低建筑结构的动力响应。

国内外许多学者对相邻结构间设置阻尼器进行了大量研究。Bhaskararao等[4]研究了设置摩擦阻尼器的相邻结构在地震激励下的动力响应，研究表明阻尼器的连接位置对减震效果有明显影响。Zhu等[5]针对设置Kelvin或Maxwell黏弹性阻尼器的相邻结构分别在时程激励和Kanai-Tajimi谱的随机激励下对阻尼参数优化分析，研究表明两类阻尼器的最优参数依赖于结构的总质量和第一阶固有圆频率。吴巧云等[6]对相邻结构设置Maxwell型黏弹性阻尼器的位置进行优化布置研究，得出了阻尼器的优化位置的布置规律。李创第等[7]研究了设置Maxwell型黏弹性阻尼器的两相邻组合体结构在胡聿贤谱地震模型下的随机地震动响应，获得了响应的封闭解。Andalibi等[8]提出了一种分析相邻结构在地震动设计反应谱下结构响应的近似方法。以上研究均针对相邻结构在地震作用下的分析，而实际上相邻结构在强风作用下也可能发生碰撞。周奎[9]对相邻等高和不等高隔震结构风振碰撞进行研究，研究表明相邻结构的风振响应随着结构周期比的增大而减小。王钦华等[10]分析了调谐质量惯容阻尼器连接的高层结构风振响应，研究表明惯容阻尼器能够有效减小连体结构的风致加速度响应。田华睿[11]分析了TLCDI和MTLCDI控制的连体建筑风振响应控制效果，研究表明TLCDI和MTLCDI对连体结构的层间位移角控制效果较好。但目前关于相邻结构间设置黏弹性阻尼器风荷载响应分析未见有相关文献报道。

鉴于黏弹性阻尼器耗能能力强、性能可靠、安装方便等优点[12-14]，本文对设置黏弹性阻尼器的相邻结构在Davenport谱荷载下的风振响应进行了研究，获得了设置黏弹性阻尼器的相邻结构风振响应解析解。首先，将广义Maxwell本构关系与结构运动方程耦合；其次，运用复模态法将联立后的运动方程解耦，并给出结构动力响应频域解的统一表达式；然后，基于频响函数二次分解法，获得了结构系列响应功率譜的二次分解式，并结合响应方差表达式，给出了组合体结构风振位移响应方差和速度响应方差的解析解；最后，通过算例与虚拟激励法求得的功率谱、谱矩结果进行对比，证明了所提方法的正确性，并对广义Maxwell模型黏弹性阻尼器的减振性能进行了研究。本文所提解法对于求解相邻结构在Davenport谱荷载下的响应谱矩，简化了计算过程，提高了计算精度，易于设置黏弹性阻尼器的相邻结构风振响应的求解。

4 算例

以两相邻钢筋混凝土框架结构为例，结构计算简图如图3所示，其左侧结构为14层，右侧结构为10层；结构阻尼采用[Rayleigh]阻尼，结构阻尼比[ξ]=0.05。左侧结构各层质量为3.80×105 kg，与之对应的层间刚度为1.13×108 N/m；右侧结构各层质量为2.25×105 kg，与之对应的层间刚度为3.34×107 N/m；两侧结构各层层高均为3.5 m，在第10层顶部设置黏弹性阻尼器。风荷载模型采用Davenport风速谱，两侧结构各层迎风面积均为140 m2，离地高度10 m，平均风速[V10]=33.5 m/s；建筑所在地风荷载地面粗糙度为A类，表面阻力系数Kr=0.001 29。取左侧结构为迎风侧，右侧结构为背风侧。广义Maxwell阻尼取两分支，其参数为：[kd0]=2.00×108 N/m； [kd1]=3.02×107 N/m； [kd2]=3.64×107 N/m； [λ1=10.0 s-1]；[λ2=12.5 s-1]。

4.1 结构响应功率谱的验证分析

图4和图5为本文所提方法得出的位移功率谱密度函数与虚拟激励法得出的结果对比图；图6和图7为2种方法（本文方法和虚拟激励法）计算出的层间位移功率谱密度函数的对比图。由图4—图7可以看出，2种方法计算出的功率谱密度函数的结果一致，说明了本文方法对功率谱转化后计算结果的准确性；结构位移功率谱密度函数与层间位移的功率谱密度函数是凹凸曲线，其凸对应着结构的振动特征值，凹为介于2个卓越振动特征值之间。文中式（24）为虚拟激励法求解功率谱密度函数表达式，可以看出，表达式较为复杂，且对其积分难以获得响应方差的解析解。式（33）为本文方法求解相邻结构风振响应功率谱密度函数的表达式，表达式形式简洁，并且方便积分运算，为后文获得结构响应方差的精确解析解打下基础。

4.2 结构响应方差的验证分析

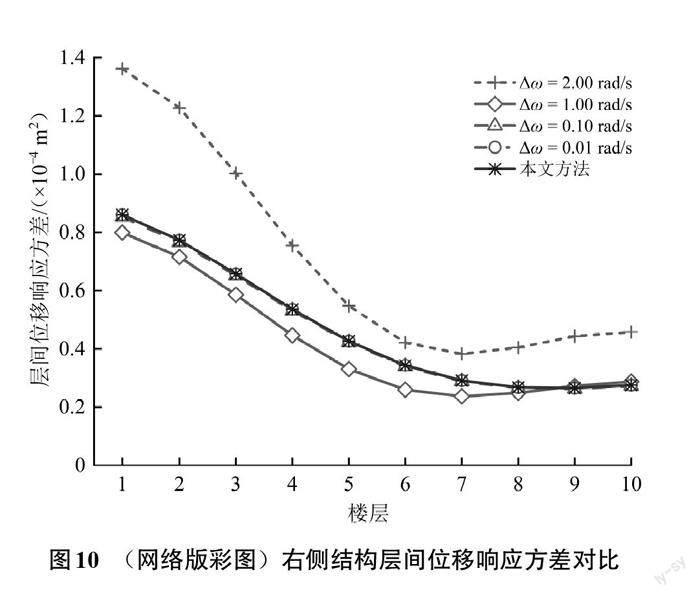
由随机振动理论可知，将式（24）代入式（35），采用虚拟激励法将其进行梯形积分运算，进而可求得结构的系列响应方差。由于梯形积分会受到积分步长的影响，间距取值只有非常小的时候，才能保证结果足够精确，虚拟激励法的计算结果受积分步长[Δω]的影响较大。因此，本文对虚拟激励法计算响应方差趋于稳定的计算结果与本文方法计算结果进行了对比，对比内容包括：位移响应方差和加速度响应方差、层间位移响应方差和层间加速度响应方差。以左侧结构的位移、速度响应方差以及右侧结构层间位移、层间速度响应方差为例，选取虚拟激励法的积分步长[Δω]分别为2.00、1.00、0.10和0.01 rad/s，积分区间为0～200 rad/s。由图8—图11可以看出，随着虚拟激励法的积分步长的减小，虚拟激励法积分步长取0.10和0.01 rad/s时，计算出的系列响应方差结果相同，可知虚拟激励法计算出的结构响应方差逐渐趋于平稳，并最终与本文计算所得的响应方差结果重合，说明了本文方法不需试算即可达到较高的精度，从而验证了本文方法的正确性。

4.3 相邻结构减振分析

对相邻结构间安装广义Maxwell型黏弹性阻尼器受控前后两侧结构的绝对位移、层间位移、层间剪力和层间位移角进行了对比。由图12可知，相邻结构间安装黏弹性阻尼器可有效降低结构的风振响应，左侧结构顶端位移减少了19.8%，右侧结构顶端位移减少了17.5%。由图13可知，设置黏弹性阻尼器后，阻尼器连接层以下的左侧结构的层间位移下降明显，右侧结构靠近连接层的3层结构层间剪力相较于未安装黏弹性阻尼器的情形，有些许增大。由图14—图15可知，相邻结构间设置黏弹性阻尼器的减振对两者中的高层建筑较为有利，对与之对应的邻近结构，距离连接层较近的下部结构顶端层间剪力与层间位移角相较于未设置阻尼器的情形，出现些许增大，因此，在相邻结构间设置阻尼器应重点考虑对较低建筑结构顶端层间剪力与层间位移角的影响。

5 结论

本文对设置广义Maxwell模型黏弹性阻尼器相邻结构在Davenport谱荷载下的风振响应进行研究，提出了一种求解风振系列响应解析解的分析方法，其主要结论如下：

1） 将广义Maxwell微分型黏弹性阻尼器本构方程与结构动力方程耦合，运用复模态法将其解耦为一阶微分方程的线性组合，得到了动态响应的统一表达式，包括绝对位移、层间位移、绝对速度和层间速度。

2） 结构的频域响应函数模值由结构振动复特征值与频域变量的组合形式给出，称之为频响函数的二次分解法，基于此获得结构风振响应方差的解析解，并用虚拟激励法验证了所提方法的准确性。研究表明本文方法計算响应方差的结果与虚拟激励法在减小积分间距后获得的响应方差的结果一致，本文方法可用于连接阻尼器的相邻结构风振响应的计算。

3） 通过相邻结构受控前后的风振响应对比，表明了黏弹性阻尼器在相邻结构中有良好的减振能力，研究表明相邻结构间设置黏弹性阻尼器能够有效降低结构风荷载下的动力响应，但需重点考虑对相对较低结构的影响，以避免低矮建筑顶端的层间剪力和层间位移角的过度增大。

参考文献

[1] 周云，梁秋河，房晓俊. 相邻结构碰撞研究进展[J]. 土木工程学报，2019，52（9）：12-22，52.

[2] 刘佩，彭凡盛，杨维国. 考虑碰撞效应的相邻框架结构地震易损性分析[J]. 建筑结构学报，2021，42（S1）：139-145.

[3] 周奎，陈玉振，黄凯. 相邻隔震建筑风致振动碰撞分析[J]. 结构工程师，2019，35（4）：131-139.

[4] BHASKARARAO A V，JANGID R S. Seismic response of adjacent buildings connected with friction dampers[J]. Bulletin of Earthquake Engineering，2006，4（1）：43-64.

[5] ZHU H P，GE D D，HUANG X. Optimum connecting dampers to reduce the seismic responses of parallel structures[J]. Journal of Sound and Vibration，2011，330（9）：1931-1949.

[6] 吴巧云，朱宏平，陈旭勇. 基于性能的相邻结构间Maxwell阻尼器优化布置研究[J]. 振动与冲击，2017，36（9）：35-44.

[7] 李创第，杨雪峰，李宇翔，等. 组合体结构基于胡聿贤谱下随机地震响应的简明封闭解[J]. 广西科技大学学报，2022，33（2）：9-16.

[8] ANDALIBI M，BEHNAMFAR F. An approximate method for separated spectral analysis of connected buildings with added damping[J]. Structural Design of Tall and Special Buildings，2019，28（10）：e1614.1-e1614.17.

[9] 周奎. 相邻隔震建筑风致振动碰撞研究[D]. 福州：福州大学，2016.

[10] 王钦华，雷伟，祝志文，等. 单重和多重调谐质量惯容阻尼器控制连体超高层建筑风振响应比较研究[J].建筑结构学报，2021，42（4）：25-34.

[11] 田华睿. TLCDI 及 MTLCDI 阻尼器控制连体超高层建筑风振响应研究[D]. 汕头：汕头大学，2021.

[12] 刘美华，邹万杰，葛新广，等. 单自由度广义Maxwell阻尼结构基于欧进萍谱随机响应的简明封闭解法[J]. 广西科技大学学报，2021，32（4）：58-64.

[13] ALAGAWANI B，AL-QARYOUTI Y H. Seismic behavior factors of steel frames braced with viscoelastic damping system[J]. Journal of  Engineering and Technological Sciences，2016，48（6）：715-742.

[14] LEWANDOWSKI R，LASECKA-PLURA M. Design sensitivity analysis of structures with viscoelastic dampers[J]. Computers and Structures，2016，164：95-107.

[15] 刘美华，邹万杰，葛新广，等. 基于欧进萍谱的广义Maxwell耗能结构随机响应简明解法[J]. 振动与冲击，2022，41（4）：124-133.

[16] 方同. 工程随机振动[M]. 北京：国防工业出版社，1995.

[17] 李暾，张梦丹，姜琰，等. 基于近似Davenport风速谱的建筑结构动力响应的新封闭解法[J]. 广西科技大学学报，2020，31（4）：1-10，18.

[18] LI C D，YANG X F，LI Y X，et al. Wind vibration responses of structure with generalized Maxwell model viscoelastic dampers[J]. Structures， 2023， 47： 425-433.

[19] 林家浩，张亚辉，赵岩. 虚拟激励法在国内外工程界的應用回顾与展望[J]. 应用数学和力学，2017，38（1）：1-32.

[20] 孙妍. 复变函数与积分变换[M]. 北京：机械工业出版社，2016.

Wind load response analysis of viscoelastic dampers between

adjacent structures

YANG Xuefeng1， LI Chuangdi*1， LI Yuxiang1， GE Xinguang2

（1.School of Civil Engineering and Architecture， Guangxi University of Science and Technology， Liuzhou 545006， China; 2.School of Civil Engineering and Architecture， Liuzhou Institute of Technology， Liuzhou 545616， China）

Abstract： Setting viscoelastic dampers between two adjacent structures can effectively reduce the dynamic response of the structures under wind load. Taking the generalized Maxwell model as the calculation model of viscoelastic dampers， an analytical solution of wind-induced vibration response of energy-dissipating structures with viscoelastic dampers between adjacent structures is proposed. Firstly， the differential constitutive relation is derived from the structure diagram of the generalized Maxwell viscoelastic damper， and it is coupled with the motion equations of two adjacent structures. Secondly， the response of adjacent structures（displacement， velocity， inter-story displacement and inter-story velocity）is expressed as a combination of first-order linear equations by using the complex mode method， and the unified frequency domain solution of the above response is obtained based on the virtual excitation method. Then， based on the frequency response function quadratic decomposition method， the analytical solution based on the Davenport wind speed spectrum and considering the spatial correlation structural response variance is obtained. Finally， the correctness of the proposed method is verified by comparing the results of a numerical example with the results of the virtual excitation method， and the damping effect of the damper in the wind-induced vibration control of adjacent structures is analyzed.

Key words： adjacent structures; generalized Maxwell viscoelastic dampers; Davenport wind speed spectrum; quadratic decomposition method of frequency response function; vibration damping effect

（责任编辑：罗小芬）