基于Sobol法的五轴工具磨床几何误差辨识

潘英广 唐清春 袁秀坤 张晨阳 魏巍 王太子

摘 要：机床的加工精度受诸多方面的误差影响，包括力、热、几何、运动等误差，其中几何误差影响较大。本文以自主研发的五轴工具磨床为研究对象，研究该磨床存在的几何误差影响程度，为该磨床在后续使用过程中进行误差补偿提供理论依据。首先，基于多体系统理论建立磨床的拓扑结构，确定了该磨床结构空间存在的37项几何误差；其次，利用体间齐次坐标变换矩阵理论建立了磨床综合误差模型；最后，使用Sobol全局灵敏度分析法与准蒙特卡罗估算法对磨床误差模型进行分析，计算出各几何误差项对整体几何误差空间的影响程度。结果表明：在磨床的37项几何误差中，影响该磨床空间几何误差较大的误差项为偏摆角误差与滚转角误差，为后续的误差补偿提供了理论依据。

关键词：五轴工具磨床；几何误差；多体系统理论；全局灵敏度分析

中图分类号：TG580.1 DOI：10.16375/j.cnki.cn45-1395/t.2023.03.004

0 引言

数控机床被喻为“工业母机”，其加工精度已成为最重要的产品质量指标之一[1]，而机床的精度直接决定着零件的加工精度，故提升数控机床加工精度极为重要。对于零件来说，影响其加工精度的因素有很多，例如机床几何误差、装配误差、系统误差、力学误差、热误差等，对此，国内外诸多学者进行了大量的研究。杨建国等[2]研究表明，机床的几何误差占机床总误差的30%～45%，因此，研究机床的几何误差对机床的设计与精度提升具有重要的工程应用价值与意义。Yao等[3]对某车削机床进行误差分析，通过局部灵敏度分析，辨识出8项关键几何误差，并进行了试验验证。王勇等[4]基于多体系统理论对QMB125球笼沟道磨床建立几何误差模型，并对其进行灵敏度分析，辨识对该磨床影响较大的误差项。范晋伟等[5]基于多体系统理论建立起某数控内圆磨床的几何误差模型，并计算其各自灵敏度系数，为后期机床误差补偿提供了参考。

由以上文献可知，目前在机床几何误差分析中采用的灵敏度分析方法均为局部灵敏度分析法，即只考虑单个误差因素对模型的影响程度，而没有考虑误差项因素之间的耦合特性对整体模型的影响。全局灵敏度分析法则弥补了局部灵敏度分析法的缺陷，不仅考虑单个误差项对整体模型的影响，而且考虑了不同参数之间耦合作用下对整体模型的影响。全局灵敏度分析法主要有基于方差的Sobol法、Morris法、Fast法等，其中Sobol法為一种全局的、定量的、无模型的分析方法，广泛应用于机械、水文、物理、城市规划等领域[6]。杨德友等[7]利用Sobol法计算各参调发电机组的全局灵敏度，确定关键发电机组并进行优化，实现在区间弱阻尼模式下阻尼的有效提升。周如意等[8]采用Sobol法筛选出轮地模型中的主导参数，用于反映底面承压特性与剪切特性的变化。吴杨俊等[9]利用Sobol法对动力包隔振参数进行灵敏度分析，确定影响较大的参数，最后对主要影响参数进行优化，使动力包系统隔振性能指标得到改善。

由于五轴工具磨床有高速、高效、高精度的要求，采用局部灵敏度分析法分析几何误差难以精准地预判几何误差各项对机床误差整体的真实影响程度。本文以自主设计五轴工具磨床为对象，利用多体系统理论法对磨床整体几何误差建立空间模型，基于Sobol灵敏度分析法辨识影响磨床整体几何误差较大的主要误差项，为机床误差补偿提供理论依据。

1 五轴工具磨床及其误差分析

1.1 五轴工具磨床结构

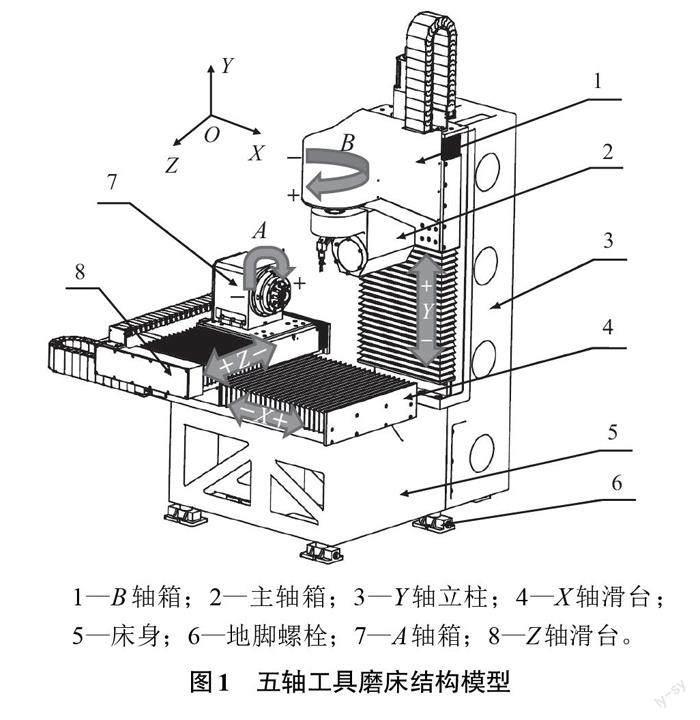
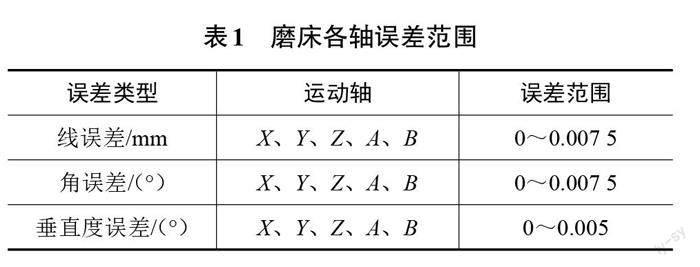
本文研究对象为自主研发五轴工具磨床，如图1所示，其外观尺寸为1 487 mm×1 571 mm×1 925 mm。该磨床主要由床身、立柱、XZ轴组件与Y轴组件等构成，共有5个运动轴，其中X、Y、Z为3条平动轴，A、B为旋转轴。采用被加工件轴线卧式布局，工件安装在XZ轴组件上，加工时工件可实现X、Z轴方向移动与A轴回转运动。砂轮主轴箱与B轴组件设置在立柱（Y轴）上，可沿Y轴上下运动和B轴回转运动。为保持磨床高精度的优良特性，设计各轴误差范围如表1所示。

1.2 磨床几何误差项分析

磨床中的每个构件都具有6个自由度，由于磨床装配误差及定位误差等因素的影响，每个自由度在空间中形成磨床的几何误差。6个自由度误差可归为移动副误差与转动副误差，分别用[δ]、[ε]表示。当X轴做平移运动时，X轴的6个自由度误差分别为：1个定位误差[δx（X）]，2个直线度误差[δy（X）、δz（X）]，滚转角误差[εx（X）]，偏摆角误差[εy（X）]和俯仰角误差[εz（X）]，其磨床误差如图2所示。运动件之间除了上述6个误差之外还有平行度误差与垂直度误差，其中，将两轴夹角大于90°的方向定义为垂直度误差的正方向。通过分析磨床结构与运动件之间的关系可知磨床存在37项空间几何误差项，所有误差项如表2所示。

2 五轴工具磨床几何误差建模

2.1 磨床拓扑结构

根据多体系统理论，可利用低序体阵列来描述机床拓扑结构，引入齐次坐标变换矩阵，再结合各个体之间的位姿状态关系精确地描述出个体实际情况的位姿状态表达式[10-11]。拓扑结构即是描述一个多体系统中各个体之间的关系，在多体系统中，每一个构成拓扑结构的刚体即为一个单元体，而低序体阵列是对该系统拓扑结构进行描述时利用最多的一种方法，其做法为：将五轴工具磨床视为一个多体串联系统，建立2条运动链，其中床身作为惯性体标记为0，与其相连且逐渐远离的标记为1、2、3甚至更多，则运动链可表示为①床身→工件（0-1-3-4-5），②床身→刀具（0-2-6-7）；同时建立各组件坐标系，静止时磨床主轴方向为Z轴，其余XY轴采用右手笛卡尔坐标系确定，设定磨床坐标系与床身坐标系重合，磨床各坐标系设定如表3所示，简图如图3所示，拓扑结构图如图4所示。

3.3 磨床几何误差项灵敏度分析

由于磨床的精度受到各个几何误差项的影响程度不同，因此利用Sobol全局灵敏度分析法对该五轴工具磨床综合空间误差模型进行分析，便于识别关键几何误差项。

磨床空间几何误差模型中有37项几何误差参数，模型样本取值数量越多估算精度值越精确。为保持磨床的精度，模型估算采样数量N设为N=30 000，各个几何误差项范围通过控制压缩系数来保证磨床的设计精度，所采取的各个几何误差项均為标准值的2倍，线误差取0～0.015 mm，角误差取0～0.015°，垂直度误差取0～0.01°，磨床误差项取值范围如表6所示。

除上述几何误差项取值范围外，还需确定各体之间的相对位置坐标以及A、B旋转轴的旋转角度。为简化计算模型，A、B轴旋转角设为非0恒定值，设置磨床Z轴坐标系与A轴坐标系重合，最后通过Matlab软件编制Sobol灵敏度分析程序，每个误差项依次编号1—37，计算磨床几何误差模型灵敏度系数，结果如图6所示，[Si]表示一阶灵敏度系数，[STi]表示总灵敏度系数。

3.4 仿真结果分析

由上述灵敏度分析结果可知，一阶灵敏度系数[Si]与总体灵敏度系数[STi]几乎相等，说明磨床中某一几何误差项不受其他误差项影响，即误差项之间耦合作用较小，在研究误差补偿时可考虑单个误差。关键几何误差项如表7所示。

由图6（a）与表7可知，X方向影响较大的几何误差项第11项即Y轴的偏摆角误差[εyY]，占X方向总误差约66%；其次是第6项即X轴的俯仰角误差[εzX]，占X方向总误差约21%，其余项均可忽略不计。

由图6（b）与表7可知，Y方向影响较大的几何误差项为第10项、第32项、第6项，即Y轴的滚转角误差、Y轴的垂直度误差以及X轴的俯仰角误差[εxY、VZY、εzX]，分别占Y方向总误差的45%、20%、17%，其余项均可忽略不计。

由图6（c）与表7可知，Z方向受几何误差项影响较大的为第5项、第4项、第17项，即X轴的偏摆角误差、X轴的滚转角误差以及Z轴的偏摆角误差[εyX、εxX、εyZ]，分别占Z方向总误差的30%、25%、12%，其余项均可忽略不计。

综上，在后续精度设计与误差补偿时应当注意影响较大的误差项，同时在磨床零件加工或装配阶段应保证工件精度及各构件间的位置度，以减小偏摆角误差等重要误差因素。

4 结论

以五轴工具磨床为研究对象，对磨床进行误差分析，得出影响磨床的37项误差，并基于多体系统理论，通过低序体阵列来描述磨床的拓扑结构，建立其空间几何误差模型；采用Sobol全局灵敏度分析方法，通过准蒙特卡罗采样方法以磨床几何误差项作为输入变量，最后估算磨床灵敏度系数，得出以下结论：

1）Sobol全局灵敏度分析法能精确地分析出磨床各项误差的灵敏度系数，有利于对影响加工精度的因素进行筛选，对后续的磨床误差补偿提供理论支撑。

2）在37项磨床几何误差元素中，影响磨床几何误差较大的误差项均表现为偏摆角误差，占空间总误差30%～66%；其次是滚转角误差，占总误差的45%。

3）通过分析结果可知，该方法也可用于同类其他磨床的误差分析，有利于磨床后续的精度设计及装配，为合理、经济地提高磨床精度设计提供理论参考。

参考文献

[1] 樊嘉，郑华林，何勇，等. 机床关键几何误差元素辨识及其公差设计方法[J].航空制造技术，2021，64（22）：56-64.

[2] 杨建国，范开国，杜正春. 数控机床误差实时补偿技术[M].北京：机械工业出版社，2013．

[3] YAO H H，LI Z Q，ZHAO X S，et al.Modeling of kinematics errors and alignment method of a swing arm ultra-precision diamond turning machine[J].The International Journal of Advanced Manufacturing Technology，2016，87（1-4）：165-176.

[4] 王勇，刘洋，朱嘉敏，等. QMB125球笼沟道磨床几何误差建模与敏感度分析[J].机械设计与制造，2022，373（3）：30-35，40.

[5] 范晋伟，秦池，潘日，等. 数控内圆复合磨床几何误差建模及灵敏度分析[J].工具技术，2021，55（8）：96-100.

[6] 司癸卯，展梓荃，高康平，等. SEA模型的参数全局灵敏度分析[J].机械科学与技术，2021，40（10）：1491-1496.

[7] 杨德友，赵康，王丽馨. 基于全局灵敏度的区间模式阻尼提升策略[J].电力自动化设备，2021，41（11）：113-119.

[8] 周如意，丰文浩，邓宗全，等. 轮地力学模型参数灵敏度分析与主参数估计[J].航空学报，2021，42（1）：253-265.

[9] 吴杨俊，徐翠强，陈杰，等. 内燃动力包隔振参数灵敏度分析及优化设计[J].中南大学学报（自然科学版），2021，52（11）：3872-3884.

[10] 刘又午，刘丽冰，赵小松，等. 数控机床误差补偿技术研究[J].中国机械工程，1998（12）：48-51.

[11] 李庄. 五轴机床运动学通用建模理论研究及应用[D].成都：西南交通大学，2013.

[12] 荣茂林，胡腾，何郑曦，等. 基于Sobol法的机床关键几何误差元素辨识方法研究[J].机床与液压，2022，50（3）：95-99.

[13] 吴文军，黄中烈，岳宝增. 带多充液圆柱箱航天器姿-轨-液耦合系统参数灵敏度分析[J].广西科技大学学报，2018，29（1）：25-30，48.

[14] 刘晓肖，王德成，程鹏，等. 弹簧成形机几何误差的完备建模及其补偿方法研究[J].机电工程，2021，38（6）：665-672.

[15] 陈冉. 超精密车床几何误差建模、分析及补偿加工研究[D].武汉：华中科技大学，2019.

[16] 杨甄鑫，廖抒华，石登仁，等. 基于接头与截面灵敏度分析的白车身结构改进[J].广西科技大学学报，2022，33（1）：7-11.

Geometric error identification of five-axis tool grinder

based on Sobol method

PAN Yingguang1， TANG Qingchun*1， YUAN Xiukun2， ZHANG Chenyang1， WEI Wei1， WANG Taizi1

（1.School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology， Liuzhou 545616， China; 2. Department of Transportation Engineering， Sichuan Vocational and Technical College of

Engineering， Deyang 618000， China）

Abstract： The machining accuracy of machine tools is affected by the force， heat， geometry， motion and other errors， among which the geometric error plays a vital role. In this paper， the independently developed five-axis tool grinder is taken as the research object to study the influence of geometric errors of the machine tool， so as to provide a theoretical basis for error compensation in the subsequent use of the machine tool. Firstly， the topological structure of the grinder is established based on the multi-body system theory， and 37 geometric errors in the structure space of the grinder are determined; Secondly， the comprehensive error model of grinder is established by using homogeneous coordinate transformation matrix theory between bodies; Finally， Sobol global sensitivity analysis method and quasi Monte Carlo estimation are used to analyze the grinder error model， and the influence degree of each geometric error item on the overall geometric error space is calculated. The results show that among the 37 geometric errors of the grinder， the error items that affect the grinder's spatial geometric error are deflection angle error and roll angle error， which provides a theoretical basis for the subsequent error compensation.

Key words： five-axis tool grinder; geometric error; multi body system theory; global sensitivity analysis

（責任编辑：黎 娅）