构建同构式 感悟对称美*

江苏省扬州中学 (225007) 褚玉霞

江苏省扬州市教育科学研究院 (225009) 戚有建

数学中的同构式指的是除了变量不同,而结构完全相同的两个式子,同构式体现了数学的对称美与和谐美．解题时若能从“同构”入手,不仅可以另辟蹊径、出奇制胜,起到事半功倍的效果,同时还能够赏析数学的结构之美和独特魅力．同构式在求值、方程、不等式、数列、解几等方面都有着很好的应用,下结合几道例题加以说明．

一、在求值中的应用

例1 若2x2e2x+lnx=0,则2x+lnx=.

分析：本题是超越方程,不方便解出x0,可以从已知式的结构入手,挖掘式子中隐含的特征,对其变形,改写成同构式,然后寻求解题思路.

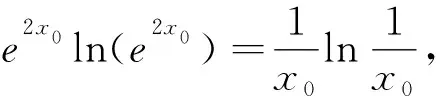
二、在方程中的应用

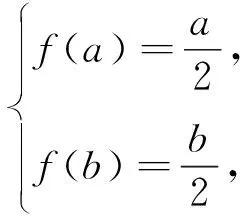
点评：一般地,若实数a,b分别满足f(a)=0,f(b)=0,则它们呈现同构特征,所以a,b可视为方程f(x)=0的两个根,于是想到构建方程或函数,利用方程根的特征或函数的性质来解决问题．

三、在不等式中的应用

分析：本题如考虑分参则分不起来,若考虑构建差函数则差函数的导数会很繁杂.实际上,本题可以挖掘结构特征、构建同构式,转化为单调性来处理,难点是如何改写成同构式.

点评：如果不等式的两侧呈现的是同构特征,则可由相同的结构构建函数,进而转化为函数的单调性问题,据此可用来比较变大小或解不等式．

四、在数列中的应用

例4 设各项均为正数的数列{an}的前n项和为Sn,且a1=1,(Sn+1+λ)an=(Sn+1)an+1,n∈N*．

(1)若λ=1,求数列{an}的通项公式;

(2)求实数λ的值,使数列{an}是等差数列．

(2)先由a1,a2,a3成等差数列得λ=0,代入已知,再证明此时数列{an}是等差数列.

点评：两小题都是通过变形,将递推关系式改写成“依序同构”的特征,从而构建“常数列”来解决问题.

五、在解几中的应用

例5如图1,过抛物线y=x2上的点A作圆M:x2+(y-2)2=1的两条切线,分别交抛物线于B,C两点,证明:直线BC与圆相切.

图1

分析：由于三个点A,B,C的地位等同,所以三条直线AB,AC,BC的方程结构相同,所以可以构建同构式来处理.

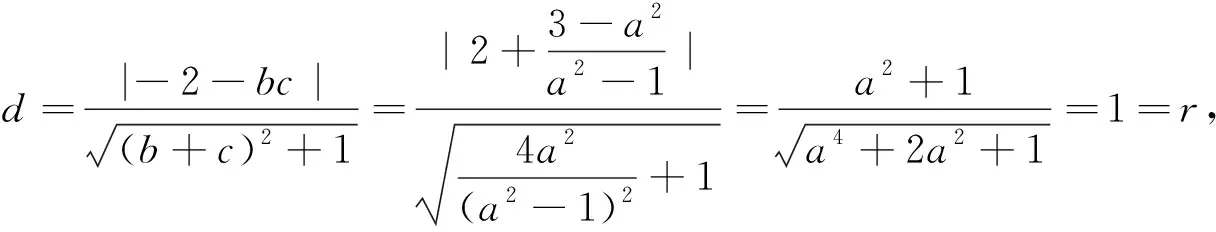
点评：本例中三条直线AB,AC,BC方程的结构相同,所以可以挖掘同构式,构建一元二次方程,利用韦达定理让问题顺利解决.在解析几何中,善用“同理”,可以提升整体运算能力,极大减少解几的繁琐运算．

通过上面几道例题可以发现,利用同构思想来处理问题,求解的关键在于深入剖析代数式的结构特征,将代数式进行不断的变形和转化,直到出现结构完全相同的两个式子,然后抽象出一个函数,借助该函数的单调性来寻求解题思路．利用同构思想来处理问题有利于培养学生敏锐的观察能力、丰富的想象能力、灵活的构造能力和高超的创造能力．同构式体现了 “数学运算”与“数学抽象”两大数学核心素养的完美融合,彰显了数学的科学价值、应用价值和审美价值．