两道条件概率题的辨析*
广州大学附属中学 (510006) 朱惊涛
新人教A版教材使用以来,对条件概率的考查成为热点,然而在一些地方命制的高三模拟试题中,出现了试题命制不严谨或者答案有误的情况,分析这类题目,有助于增进我们对于条件概率问题的理解,试举以下两例进行分析:
例1 (2022年某市高三模拟题)高压钠灯使用时发出金白色光,具有发光率高、耗电少、寿命长、透雾能力强和不锈蚀等特点,广泛应用于机场、码头、船坞、车站、广场、街道交汇处等地方. 现在某公园中心树立有一灯杆,杆上装有6盏高压钠灯,每盏灯各使用灯泡一只,且型号相同. 假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为p1,寿命为2年以上的概率为p2,从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
(1)在第一次灯泡更换工作中,求①不需要更换灯泡的概率;②更换2只灯泡的概率;
(2)当p1=0.8,p2=0.3时,求在第二次灯泡更换工作中,至少需要更换5只灯泡的概率(结果保留两个有效数字).

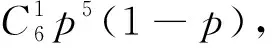

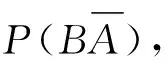
例2 (2022年某市高三模拟题) 某学校食堂开设一楼、二楼、三楼三个学生餐厅,A同学一天午餐随机地选择一个餐厅就餐.如果中午去一楼餐厅就餐,那么当天晚上不去一楼就餐的概率等于0.9;如果中午去二楼餐厅就餐,那么当晚去二楼就餐的概率等于0.7;如果中午去三楼餐厅就餐,那么当晚不去三楼就餐的概率等于0.8.还知道A同学晚上选择在一楼与三楼就餐的概率相等.那么,A同学晚上选择在一楼、二楼、三楼就餐的概率分别等于( ).
该题参考答案:
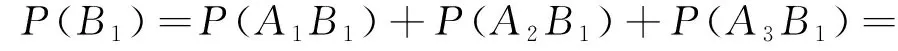
答案辨析:按题目条件给出的是“A同学晚上选择在一楼与三楼就餐的概率相等”,应该解读为P(B1)=P(B3),但是在该标准答案中,将这一条件理解为“P(B1|A2)=P(B3|A2)、P(B1|A3)=P(B3|A3)、P(B1|A1)=P(B3|A1)”,那么这两者是否等价呢?答案是否定的.分析如下:
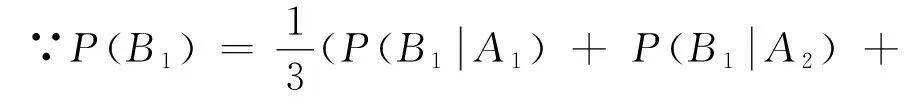
详细可整理如下表:

P(B1A1)=0.1P(B2A1)=0.6P(B3A1)=0.3符合“中午去一楼,当天晚上不去一楼概率等于0.9”P(B1A2)=0.2P(B2A2)=0.7P(B3A2)=0.1符合“中午去二楼,当天晚上去二楼概率等于0.7”P(B1A3)=0.3P(B2A3)=0.5P(B3A3)=0.2符合“中午去三楼,当天晚上不去三楼概率等于0.8”