非平坦宇宙中相互作用的鬼场暗能量模型①

袁通全， 张德维

1.河池学院 数理学院，广西 河池 546300；2.马来西亚英迪国际大学 工程学系，尼莱 71800，马来西亚

1 鬼场暗能量模型

2 相互作用鬼场暗能量模型

相互作用鬼场暗能量模型假定冷暗物质和暗能量之间存在非引力相互作用.而且, 假定暗能量来自鬼场的贡献.由于WMAP 5年的数据[56]在95%的置信度水平下约束现有宇宙的曲率为-0.017 5<Ωk<0.008 5, 并且鬼场暗能量是宇宙物质的一部分, 所以将平坦宇宙推广到非平坦宇宙.描述4维均匀各向同性宇宙的线元, 被称为FLRW时空, 可写成[57]:

(1)

其中:a(t)是以宇宙时t为自变量的尺度因子, 而K=-1, 0, 1分别对应于开放的、平坦的和闭合的宇宙.宇宙动力学是通过解爱因斯坦场方程:

Gμν=8πGTμν

(2)

来得到的.对于度规(1), 爱因斯坦场方程的(00)分量给出[57]:

(3)

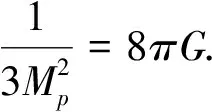
(4)

用无量纲能量密度表示, Friedman方程(3)变成:

Ωm+ΩD+Ωk=1

(5)

零压强冷暗物质和暗能量守恒方程分别被假定为:

(6)

和

(7)

(对应于引入Q项后能量动量张量Tμν的每个分量守恒), 其中ωD=PD/ρD是暗能量压强与其密度的比值, 即暗能量状态方程参量,Q(ρm,ρD)表示可以取不同形式的非引力相互作用项.本研究将非引力相互作用函数设为Q=3Hδρm,δ为相互作用因子.值得注意的是, 连续性方程意味着非引力相互作用函数应该是一个以时间倒数为单位的量(第一个自然选择可以是哈勃因子)乘以能量密度.因此, 非引力相互作用项可以取不同的形式, 例如文献[45,48]考虑了Q∝H(ρm+ρD), 选择Q的形式是最简单的, 物理意义更清晰.从等式(6)可以得出ρm=ρm0a-3(1-δ).为了使冷暗物质的密度随着a的增加而降低, 相互作用因子δ必须小于1.然而, 观测到暗能量状态方程参量的当前值ωD0仍然对相互作用因子δ有更严格的限制.利用(4)式中无量纲的能量密度,(6)式变为:

(8)

同时(7)式变成:

(9)

由(5)、(8)和(9)式可得:

(10)

(11)

从而暗能量状态方程和无量纲暗能量密度分别为:

(12)

和

其中已经令a=a0=1时,H=H0,ΩD=ΩD0.由(3)式可得:

(13)

应该注意的是, 与(13)式一起还有另一个解是E(a= 1)=0, 对应于最后缩小的宇宙, 被省略了.因此:

ΩD=ΩD0E-1,Ωm=Ωm0E-2a-3(1-δ),Ωk=Ωk0a-2E-2

(14)

这些能量密度是解析形式的.图1显示了无量纲能量密度随宇宙尺度因子a的变化, 图2显示了无量纲能量密度随相互作用因子δ的变化, 其中取Ωm0=0.26,ΩD0=0.73和Ωk0=0.01.图1中相互作用因子δ=0的线对应于冷暗物质与暗能量间不存在相互作用的情况.图像显示, 随着宇宙尺度因子a的增加, 在没有非引力相互作用的情况下, 冷暗物质的无量纲能量密度从初始最大值逐渐减小, 而无量纲暗能量密度由于鬼场的贡献而从最小值逐渐增加.非引力相互作用的出现, 使得冷暗物质的能量密度立即降低, 即转化为暗能量.这是因为ωD0的天文观测值要求相互作用因子δ为正, 导致非引力函数Q为正值.与文献[58]不同, 其中Q=3Hδ(1+ωD)ρD, 对于ωD>-1的情况, 能量从冷暗物质到暗能量流动, 而对于ωD<-1, 能量流动方向相反.当宇宙尺度因子在图2中的4种情况下恒定时, 暗能量和冷暗物质之间的非引力相互作用使Ωm减少,ΩD增加, 即零压强冷暗物质转化为暗能量.如果当前的无量纲曲率Ωk0接近0.01(K=-1), 则宇宙是开放的.从方程可以看出, 无量纲曲率密度随宇宙尺度因子的增大而逐渐减小.在95%置信水平下, 来自WMAP 5年数据和其他观测数据的暗能量状态方程的边界为-1.29<ωD0<-0.790[56].从(12)式可以看出,ωD0和相互作用因子δ之间存在简单的反线性关系.状态方程的现值ωD0限制了δ∈(0.004 8, 0.894)的范围.不同δ值的状态方程的演变见图3.相互作用因子δ=0.378的线对应于状态方程ωD0=-1.相互作用因子δ=0,Ωk0=0时的ωD0=-0.784以及相互作用因子δ=0,Ωk0=0.01时ωD0=-0.787, 两个ωD0的值显然都超出了其观测的取值范围.因此, 可以得出结论, 宇宙是平坦的, 暗能量和冷暗物质之间的相互作用不存在, 这可能是不允许的.当然, 由于观测到的Ωk0∈(-0.017 5, 0.008 1)非常小, 可以认为宇宙是近似平坦的, 但暗能量和冷暗物质之间必须存在相互作用, 因此将Ωk0的值取为0.01.

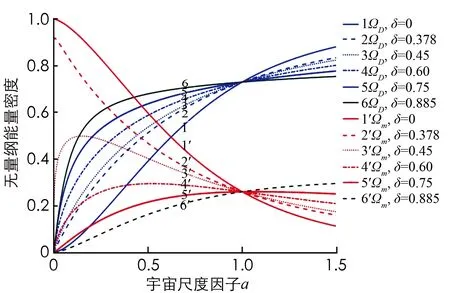
图1 无量纲能量密度随宇宙尺度因子a的变化

图2 无量纲能量密度随相互作用因子δ的变化

图3 暗能量状态方程随宇宙尺度因子a的变化

还可以计算宇宙减速参数, 其定义为:

(15)

把(11)式代入(15)式后, 可得:

(16)

能量密度Ωm,ΩD和ΩK的表达式已在(14)式给出.相对于宇宙尺度因子的宇宙减速参数见图4.可以在图4中看到, 减速参数q0(a=1)∈[-0.91,-0.38]的所有值均为负值, 这与宇宙加速膨胀的天文观测结果一致.本研究的结果与参考文献[59]一致, 其中q0=-0.48±0.1来自192颗超新星的样品数据值,q0=-0.65±0.5来自射电星系数据值.此外, 还看到宇宙减速参数与相互作用因子δ有关.相互作用越强, 减速参数越负, 宇宙加速膨胀越快.

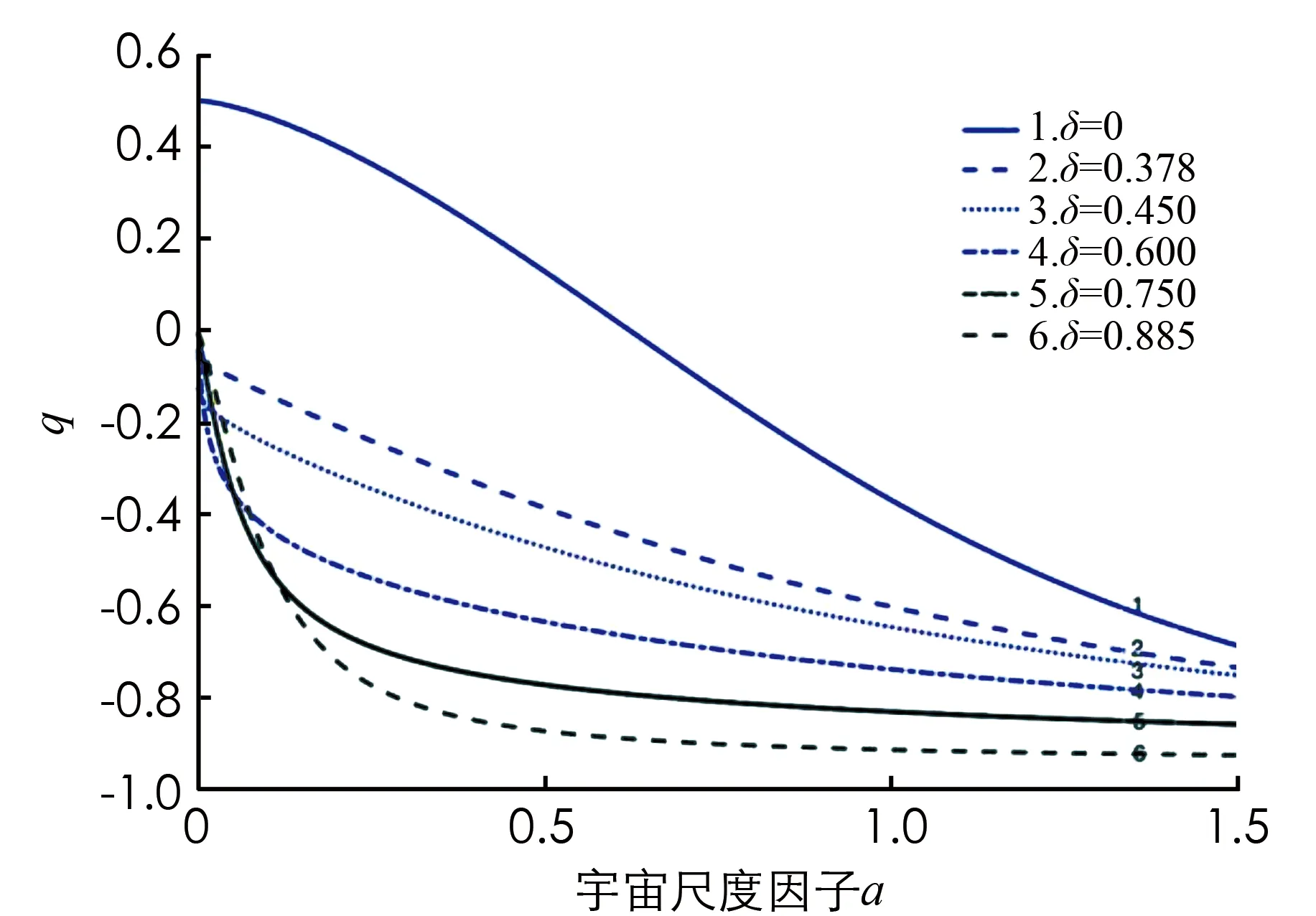
图4 宇宙减速参数随宇宙尺度因子a的变化

3 结论

本研究求解了相互作用的鬼场暗能量模型, 其中在总能量密度守恒的条件下, 可以引入冷暗物质和暗能量之间的非引力相互作用函数.该模型的优点是可以解析地给出无量纲能量密度、状态方程参数和宇宙减速因子.在原始的相互作用暗能量模型中, 非引力相互作用函数可以是正的也可以是负的, 能量转换可以是从冷暗物质到暗能量, 也可以是逆流.研究发现, 在本文给出的模型中, 冷暗物质与暗能量之间的非引力相互作用函数更倾向于正值, 这导致能量从冷暗物质转移到暗能量.相互作用因子的值是以暗能量的当前方程状态为界来选择的, 并且由相互作用因子值给出的减速因子的当前值与观测值非常一致.