梯形截面战斗部预制破片爆炸飞散数值模拟

金 鑫，肖强强，黄正祥，马 彬，祖旭东，贾 鑫

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

杀伤爆破战斗部是一种利用爆炸后产生的破片对目标进行毁伤的战斗部。传统的杀伤战斗部一般采用圆形截面,而为适应于高超声速飞行,高超声速巡航导弹战斗部舱段采用非圆形截面[1-3]。常见的非圆截面战斗部有椭圆形、菱形、梯形、鸭舌形等,其中梯形截面是主要采用的形状之一。

已有不少学者对非圆截面战斗部进行了研究。Wu等[4]提出了一种新型的螺旋弹头结构,并对不同速度椭圆弹丸撞击下钢筋混凝土结构的动力响应和破坏行为进行了数值研究。Zhou等[5]研究前圆聚能装药和后圆聚能装药组成的串联式弹头的侵彻性能时发现,在侵彻过程中,椭圆形弹体的冲蚀损伤明显大于杆状弹体。杨祥等[6]对椭圆截面杀伤战斗部破片初速周向分布进行了数值模拟,分析了椭圆长短轴之比和装药质量与壳体质量之比对破片初速的影响,得出了破片初速在长轴方向最小,短轴方向最大的结论。王钰婷等[7]对等腰梯形截面聚能装药射流成型及侵彻特性进行了研究,发现等腰梯形截面聚能装药形成的射流具有呈梯度分布的横向速度,降低了射流的侵彻深度。李鑫等[8]通过数值模拟和脉冲X光摄影实验研究了等腰梯形截面形状对聚能射流成型的影响,发现梯形截面越扁平,射流越容易横向偏移,射流越分散。马彬等[9]在Φ56 mm基准聚能装药药型罩及装药结构基础上设计了一种梯形截面聚能装药,并运用ANSYS/LS-DYNA进行了数值模拟,结果表明,梯形截面聚能装药所形成的射流容易分叉,整体形态及稳定性较差。

为了进一步研究非圆截面杀伤战斗部破片飞散特性,文中进行了5种梯形形状截面装药爆炸驱动预制破片的数值模拟,并得到了不同起爆点位置对破片飞散特性的影响规律,研究结论能够为梯形截面杀伤战斗部的设计提供依据。

1 数值模拟

1.1 梯形截面战斗部形状

文中战斗部截面形状为等腰梯形,如图1所示。为了方便地表示出不同的梯形形状,控制梯形截面的高为8 cm,短边为8 cm。通过改变梯形斜面与截面中轴线的角度θ来表示不同的梯形形状。为了尽量消除爆轰波传播过程中端面损失对破片驱动的影响,战斗部长度为50 cm,以使战斗部中部附近的破片在轴向获得相似的初速和飞散方向。文中设计了5种不同形状的梯形截面形状,即θ角分别为0°,15°,30°,45°和60°。

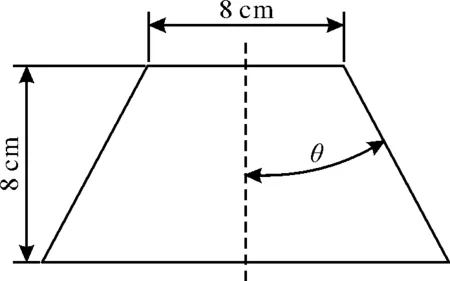
图1 梯形截面形状示意图Fig.1 Schematic diagram of trapezoidal section

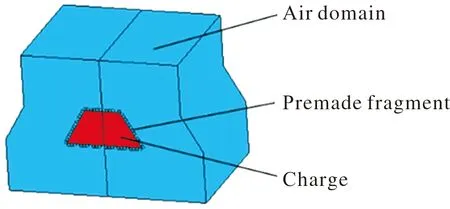
图2 有限元模型Fig.2 Finite element model

1.2 有限元模型

采用ANSYS/LS-DYNA软件建立梯形截面杀伤战斗部模型,有限元模型由炸药、空气域、预制破片组成。预制破片为6 mm立方体,均匀排列在梯形炸药四周。随着梯形截面θ的增大装药量也增大,同时破片数量也增多,为了抵消装药量变化的影响,在排列破片时对破片数量进行调整,使装药比保持一致。由于起爆点设置在梯形截面的中轴线上,也位于战斗部长度方向的中点,为节省计算资源,模型采用四分之一建模,对称面上设置对称约束。为了更好地模拟大变形,炸药和空气域采用任意拉格朗日-欧拉(ALE)算法,添加ALE多物质单元定义,预制破片的变形程度较小,采用拉格朗日算法。采用流固耦合算法来模拟炸药与预制破片之间的相互作用。空气域的厚度能够保证预制破片的速度稳定之前破片处于空气域中,在空气域边界设置无反射边界,以模拟无限大空气域。

1.3 材料模型和状态方程参数

所建立的模型涉及的材料有炸药,预制破片和空气。仿真中炸药选择B炸药,采用高能炸药计算模型(*MAT_HIGH_EXPLOSIVE_BURN)[10],密度ρ0=1.712 g/cm3,爆速D=7890 m/s,爆压(C-J压力)PCJ=29.5 GPa。炸药状态方程采用*EOS_JWL[10]定义,具体参数如表1所示。

表1 B炸药状态方程参数Table 1 Parameters of equation of state of explosive B

空气的本构模型用*MAT_NULL[10]定义,采用线性多项式(*EOS_LINEAR_POLYNOMIAL)[10]来描述空气的状态方程,其中ρ为空气密度,取1.29×10-3g/cm3,C0～C5为与空气性质相关的多项式方程系数,具体参数如表2所示。

表2 空气材料参数Table 2 Parameters of air

预制破片的材料为钨合金,材料模型为*MAT_JOHNSON_COOK[10],对预制破片状态方程的描述采用GRUNEISEN状态方程(*EOS_GRUNEISEN)[10],具体参数见表3和表4。

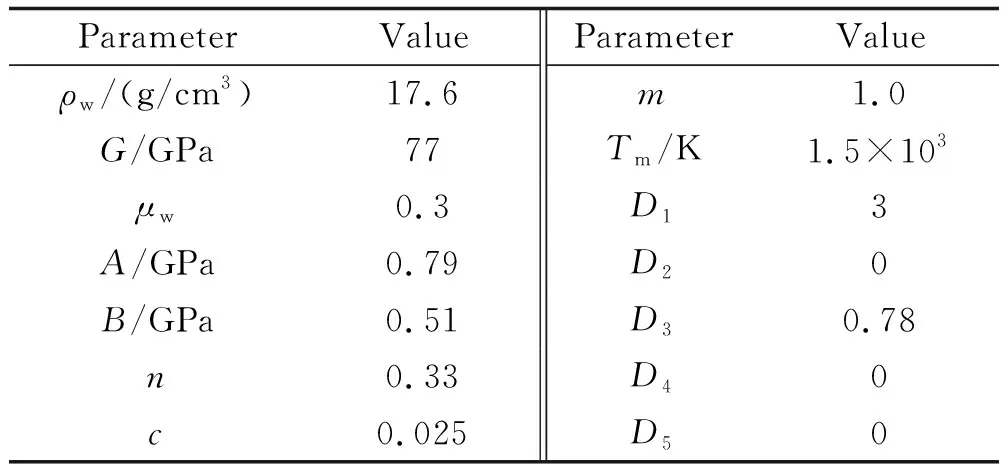
表3 预制破片材料模型参数Table 3 Parameters of prefabricated fragment

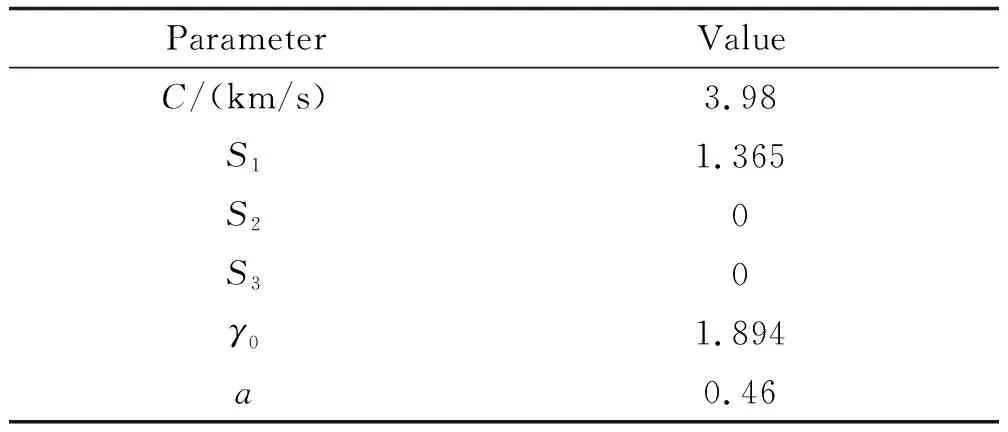
表4 预制破片状态方程参数Table 4 Parameters of equation of state of prefabricated fragment

表3中ρw为密度,G为剪切模量,μw为泊松比。

2 结果和讨论

2.1 不同梯形截面形状装药的爆轰过程

基于ANSYS/LS-DYNA软件对不同梯形截面装药爆炸驱动预制破片的过程进行数值模拟,起爆点设置在梯形中部截面中轴线上,到梯形上下边的距离相等。如图3所示,为4 μs时战斗部中部截面上压力云图。爆轰波在装药内部以球形波形式传播,爆轰波同时传播到梯形装药的上下表面,驱动破片向外飞散。当θ=0°,即装药截面形状为正方形时,显然爆轰波同时到达截面四边中点,随着θ的增大,爆轰波首先到达梯形截面上下边。之后到达梯形两条斜边。θ越大,爆轰波到达梯形斜边的时间越晚,且爆轰波最先接触梯形斜边的位置越靠近上部。随着时间的推移,斜边上部的破片已经被爆轰产物驱动,而斜边下部的破片还未受到爆轰波影响,θ越大,梯形截面斜边越长,这种时间差越大。

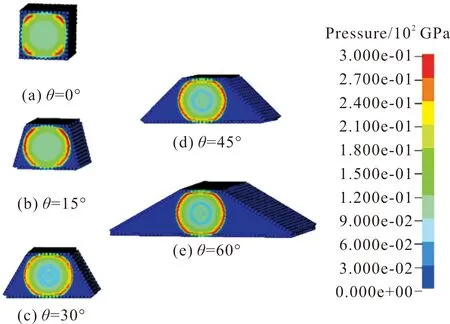
图3 4 μs时刻战斗部中部截面上压力云图Fig.3 Pressure on middle section of warhead at 4 μs

之后随着爆轰产物的向外膨胀,爆轰产物在棱角处开始泄露,如图4所示。有关研究表明[11],爆轰产物的泄露与装药和壳体的曲率有关,假设爆轰瞬时完成,破片近似沿壳体法向方向飞散。在梯形上下边与斜边的棱角处,壳体法向方向突然变化,破片沿不同的方向向外飞散,破片之间的周向间隙不断变大,引起爆轰产物泄露。对于梯形上下边和斜边上的破片,由于分别处在同一个平面上,破片近似沿相同的方向飞散,周向间隙变化不大。因此爆轰产物的泄露主要位于梯形棱角处。

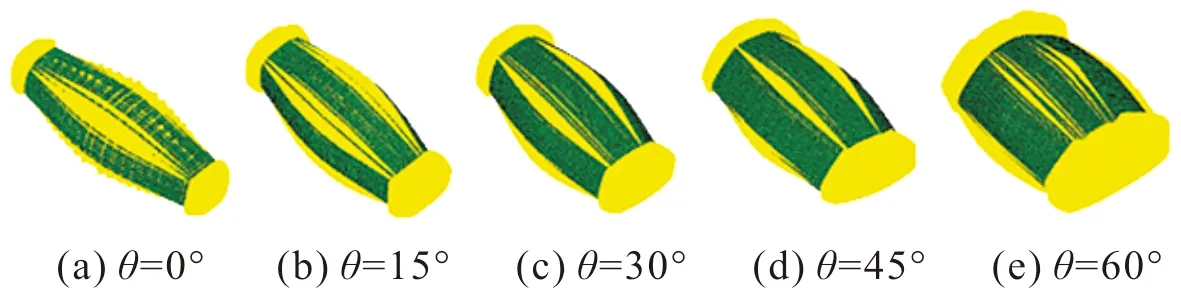
图4 爆轰产物泄露Fig.4 Leakage of detonation product

2.2 不同梯形截面形状的破片飞散情况

炸药起爆后,爆轰产物驱动破片向外飞散,图5为120 μs时各种梯形截面形状装药破片飞散情况。破片在战斗部轴向呈弧形分布,中部破片速度大,两端破片速度小。从理论上来看主要是由于爆轰产物在端面的泄露导致压力下降,对破片的驱动能力降低,因此两端破片速度小。

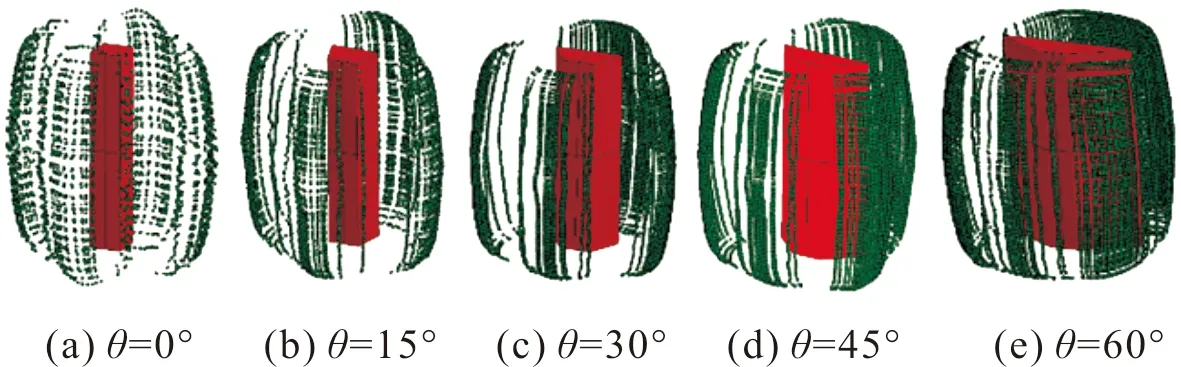
图5 120 μs时破片飞散情况Fig.5 Fragment dispersion condition at 120 μs

从图6破片的周向分布可以看出,梯形截面装药的战斗部破片在速度稳定之后,呈现出疏密相间的现象,梯形的4个面大致形成了4个破片束。梯形棱角处形成杀伤元真空区,破片主要分布在梯形各面上。这主要是梯形截面的形状造成的,各个面上的破片向外飞散的过程中,同一面上破片的飞散方向近似,而不同面上破片的飞散方向差异较大,因此形成图6中的周向分布情况。梯形上下两个面的破片分布呈外凸状,中间的破片速度最高,两边速度较低,这与爆轰产物于梯形截面棱角处泄露的情况相一致。梯形斜面上的破片飞散方向随着θ的增大朝着上方偏转,破片形成的弧形轮廓外凸处位于斜面上部位置。

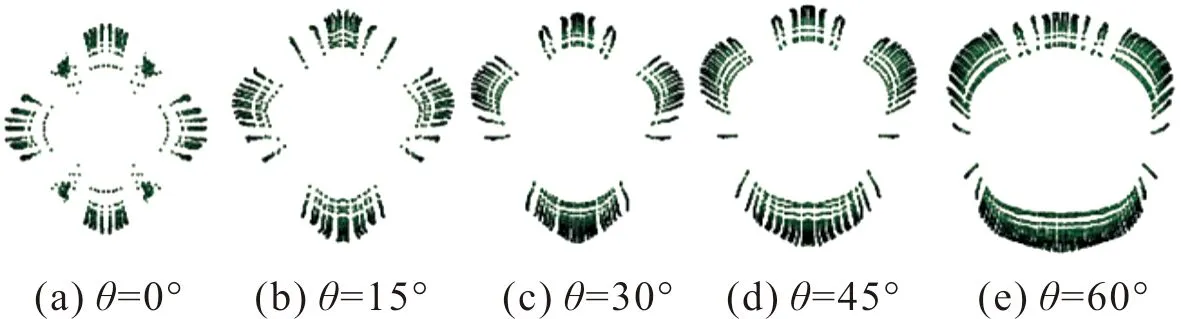
图6 破片周向分布Fig.6 Circumferential distribution of fragments

对六棱柱形战斗部预制破片爆炸飞散的靶场实验[12]表明,六棱柱形战斗部可以显著提高定向区的破片密度,具有较好的破片聚集能力。但是六棱柱棱角处的破片较少,存在杀伤元稀疏区。而梯形战斗部与六棱柱形战斗部类似,从模拟结果来看,梯形截面战斗部破片飞散分布也符合杀伤区疏密相间的规律。

为了进一步探讨梯形斜面上破片的飞散情况,对不同梯形截面形状各面上破片的周向飞散角进行了统计。图7中φ为梯形各面上的破片周向飞散角,α为偏转角,即梯形斜面上破片周向飞散角平分线与梯形截面对称轴夹角,β为梯形斜面周向飞散角平分线与斜面法向夹角。各个面上的φ值以及斜面上α值和β值分别如表5～表7所示。

表5 梯形上面破片飞散角Table 5 Flight angle of fragments on the upper surface of trapezoid (°)

表6 梯形下面破片飞散角Table 6 Flight angle of fragments on the lower surface of trapezoid (°)

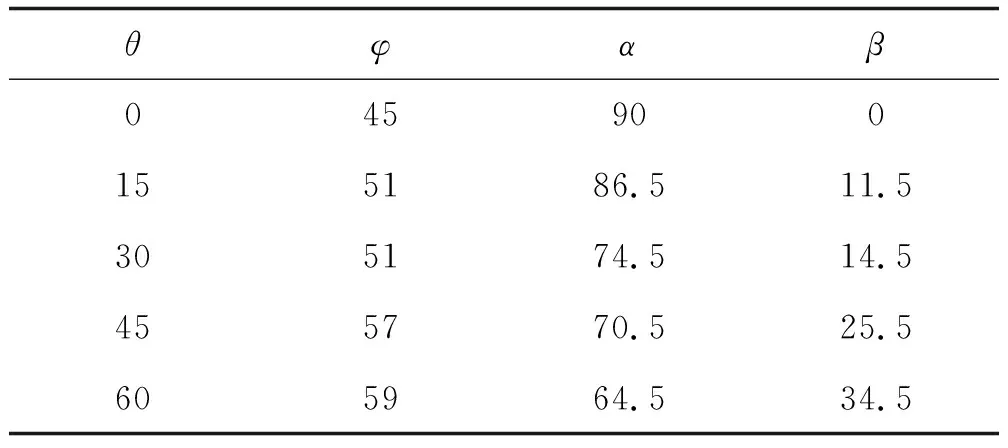
表7 梯形斜面破片飞散角与偏转角Table 7 Flight angle of fragments on the inclined surface of trapezoid (°)

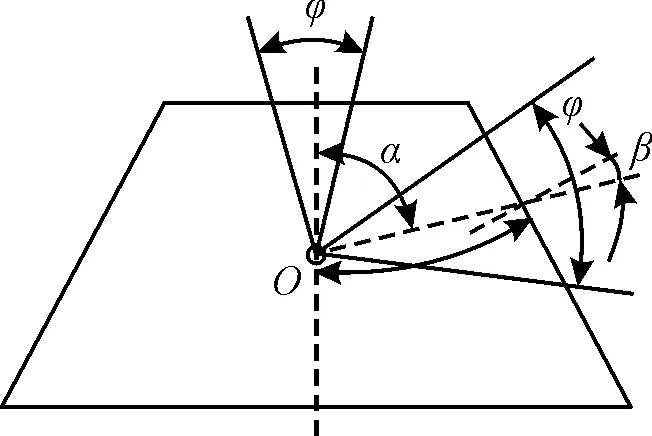
图7 破片周向飞散角示意图Fig.7 Schematic diagram of circumferential flight angle of fragments

从表7可以看出,梯形上面破片飞散角大致处于40°至49°之间,5个算例中梯形上边尺寸一致,θ的变化对于梯形上面破片飞散角的影响不大。随着θ的增大,梯形下边和斜边的尺寸变大,相应地梯形下面和斜面的破片飞散角也变大。随着θ的增大,梯形斜面上破片周向飞散角平分线与梯形截面对称轴夹角α由90°偏转至64.5°,而斜面破片周向飞散角平分线与斜面法向夹角分别为0°,11.5°,14.5°,25.5°,34.5°。由此看来,梯形斜面上破片飞散方向不沿斜面法向,相对于斜面法向朝着梯形下方偏转,θ越大,偏转程度越大。在理论上分析其原因,一是爆轰波到达斜面上破片处的时间不一致,由于爆轰产物在梯形棱角处泄露造成能量损失,爆轰产物做功能力下降,因此驱动斜面上各个破片的冲量并不相等。二是随着θ从0°增大到60°,爆轰波从垂直入射斜面变成斜入射,且θ越大爆轰波入射角越大,这也导致了梯形斜面上破片飞散方向随着θ的增大往下方偏转。

2.3 不同梯形截面形状的破片飞散速度

破片受到爆轰产物驱动后,速度迅速增加,一定时间后到达稳定状态。θ=30°时,梯形截面形状为六棱柱形的一半,破片最大速度为2 385.52 m/s。参考文献[13]中对棱柱形战斗部的靶场实验研究,文中炸药类型与破片材料与该文献一致,激光测速靶测得棱柱形战斗部最大破片速度为2 038.65 m/s,与文中模拟结果相差约为14.5%。

随着θ由0°增长到60°,5种梯形装药破片的平均速度为1 869.8 m/s,1 969 m/s,2 009.3 m/s,2 031.3 m/s,1 983.5 m/s。分别统计5种梯形截面战斗部各面上破片的平均速度,统计结果如表8所示。

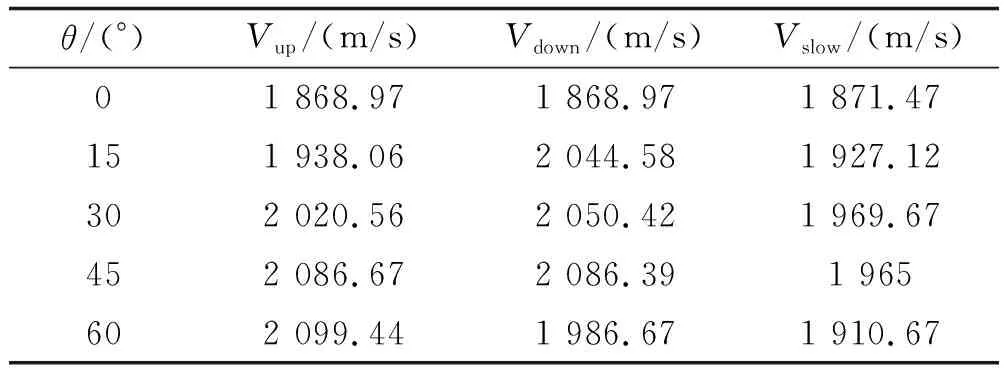
表8 梯形各面破片平均速度Table 8 Average fragment velocity on each surface of trapezoid

在θ为60°之前,在装药比保持不变的条件下,随着θ的增大,装药量增大,破片的平均速度增大,而θ为60°时破片的平均速度减小。由表8可以看出,梯形上面破片依然满足装药量越大,破片平均初速越大的规律。梯形下面的破片平均初速在θ为60°之前也随着θ的增大而增大,并且大于梯形上面的破片平均初速,在θ=60°时减小。而梯形斜面上的破片初速也随着θ的增大先增加后减小,而且相比梯形下面破片更早地在θ=45°时开始下降。

从炸药能量的角度分析其原因,随着装药量的增大,端面损失的影响越来越小,爆轰产物的大部分能量都用来驱动破片,破片速度增加。但是θ过大时梯形斜面和下面夹角过小,两个面上破片的飞散方向差异大,破片刚开始飞散便形成了较大的间隙导致爆轰产物过早泄露造成炸药能量损失,炸药对破片的做功能力大大降低。因此θ过大会降低破片的平均速度。

对于梯形截面装药破片周向速度分布,显然梯形上面和下面的破片初速中间部分最大,两边棱角处最小。为了进一步分析梯形斜面上破片初速分布规律,在战斗部中部截面梯形斜边从上到下依次选取10个破片,编号1～编号10,尽量保持间距均匀,如图8所示,统计其破片初速得到图9。

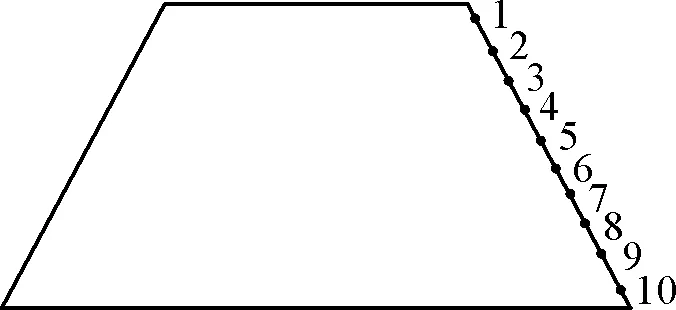
图8 斜面破片编号示意图Fig.8 Schematic diagram of fragment number on inclined plane

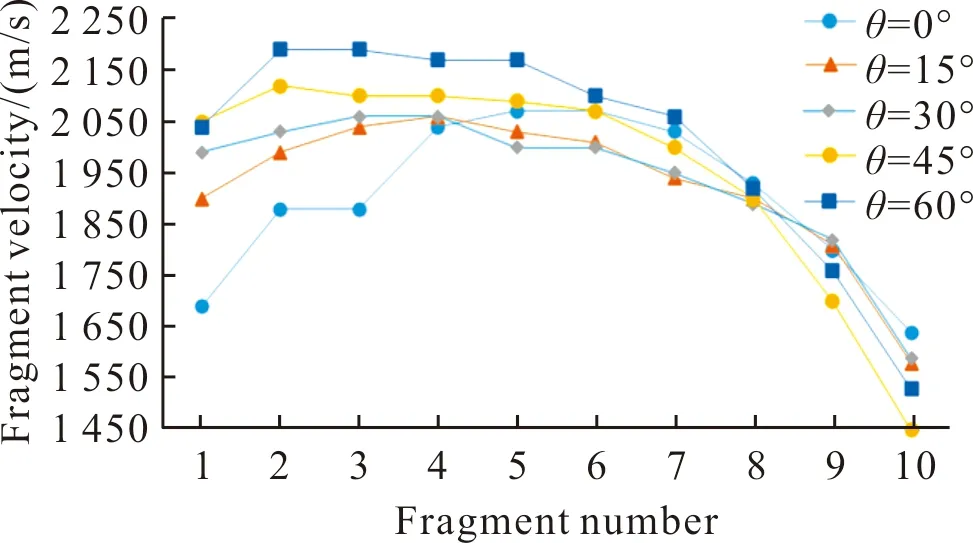
图9 梯形斜面破片初速分布Fig.9 Velocity distribution of the fragment on the inclined surface of the trapezoid

可以看出,θ=0°时,梯形斜面上破片最大速度位于编号5和编号6,θ=15°时位于编号4,θ=30°时位于编号3和编号4,θ=45°时位于编号2,θ=60°时位于编号2和编号3。说明梯形斜面上的破片靠近上方部分速度较大,下方部分破片速度迅速下降,θ越大,最大速度越靠近上方。分析其原因,除了之前提到的斜面与下面棱角处的爆轰产物泄露现象加剧,还有编号较小破片位置爆轰波接近垂直入射,θ越大起爆点至斜面的垂足越靠近编号小的破片位置。编号越大爆轰波越倾斜地扫掠过破片,入射角越大,导致炸药只有部分能量用来加速破片,因此破片速度降低。

2.4 起爆点位置对破片飞散情况的影响

为了研究不同起爆点位置对破片飞散的影响,以θ=45°梯形形状为例,在梯形中部截面对称轴上从上到下每隔2 cm取一个点作为起爆点(编号①～编号⑤),如图10所示。经数值模拟后,破片的周向分布如图11所示。

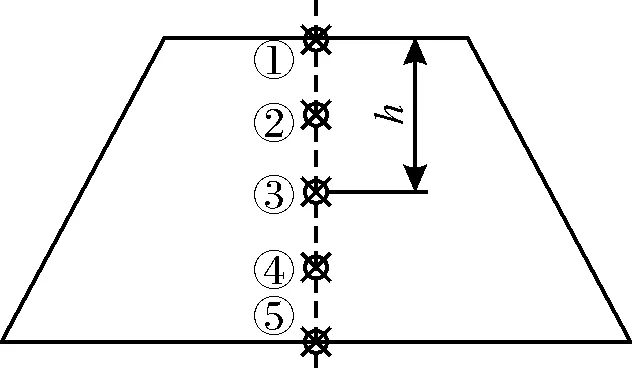
图10 起爆点示意图Fig.10 Schematic diagram of initiation points

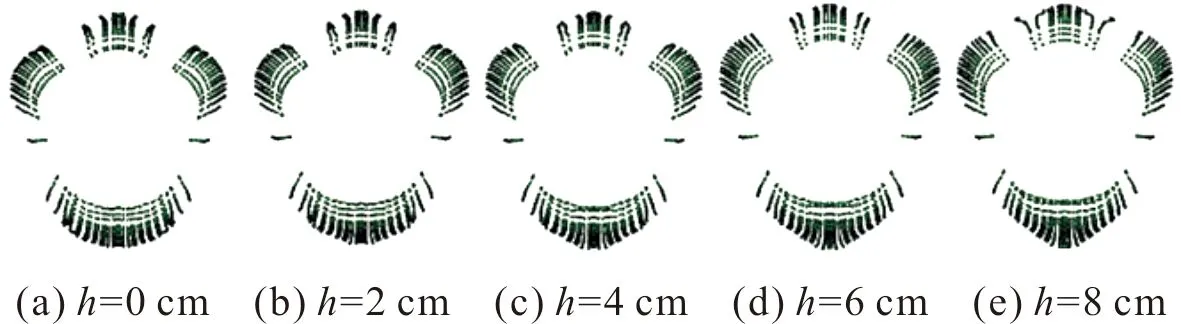
图11 不同起爆点破片周向分布Fig.11 Circumferential distribution of fragments at different initiation points

统计梯形各面上破片周向飞散角与斜面上破片偏转角,发现梯形上面破片周向飞散角集中在41°～44°,下面在93°～98°,斜面在57°～61°。这说明起爆点位置对于梯形装药破片周向飞散角影响不大。5种起爆点下斜面上的破片偏转角也都相差不大,统一在71°左右。

分别统计5种起爆点位置梯形截面各面上破片的平均速度,统计结果如图12。可以看出,随着起爆点在梯形对称轴上由上至下移动,梯形上面破片平均速度增大了6.8%,下面破片平均速度减小了3.6%,斜面破片平均速度略微提高。说明随着起爆点的远离,破片速度得到了提高,这与偏心起爆可以提高对侧破片飞散速度的研究结论相一致[14]。从能量分配的角度来看,破片远离起爆点时对应的有效装药越多,从而分配到的炸药能量越大[15]。

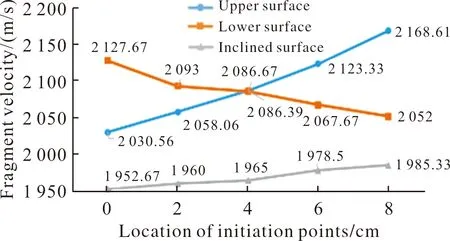
图12 不同起爆点梯形各面破片平均速度Fig.12 Average fragment velocity on each surface of trapezoid at different initiation points

3 结论

以梯形截面杀伤战斗部为研究对象,采用ANSYS/LS-DYNA软件进行了数值模拟研究,讨论了不同梯形截面形状和不同起爆点位置对破片飞散特性的影响规律,得到以下结论:

1)梯形截面装药杀伤战斗部破片飞散后呈现出疏密相间的现象,梯形的4个面大致形成了4个破片束。各个面的尺寸是影响破片飞散角的主要因素,下面破片飞散角最大,θ为60°时达到了105°。梯形斜面上的破片飞散方向相对于斜面法向朝梯形下方偏转,θ越大,偏转程度越大,最大偏转可达34.5°。

2)起爆点位于梯形对称轴中点时,在θ为60°之前,梯形各面上的破片平均速度随着θ的增大提高了8.6%,梯形下面破片速度大于梯形上面破片速度。θ达到60°会降低梯形下面和斜面上破片平均速度。梯形上面和下面中间处破片速度最大,两边棱角处破片速度最小,而斜面上速度最大的破片出现在斜面上部位置,θ越大,最大速度破片越靠近上方,最小速度位于下方棱角,相差最大为46%。

3)起爆点在梯形对称轴上不同位置对梯形各面上破片周向飞散角和斜面破片偏转角影响不大,但是可以提高起爆点对侧方向破片飞散速度。对于下面破片,上面起爆比下面起爆破片速度提高了3.7%。

4)梯形截面杀伤战斗部下面破片的杀伤性能较好,θ为45°时下面破片可获得最大的初速和较优的飞散角,飞散角达95°,同时将起爆位置设置在梯形上面可进一步提高下面破片初速,达到2 127.67 m/s。当梯形截面杀伤战斗部位于目标上方引爆可获得较好的毁伤效果。