基于多变量联合优化的MEC网络能耗最小化算法

丁嘉伟

(郑州工业应用技术学院信息工程学院，河南 郑州 451150)

0 引言

随着电子通信技术的发展,基于物联网的应用得到广泛发展,已在智慧农业、智能家居等领域大量使用。随着应用的拓展,对终端设备的计算容量也随之增加。为此,研究人员引用移动边缘计算(mobile edge computing, MEC)[1]等途径来缓解终端设备对计算容量的不足。

不失一般性,MEC服务器位于网络边缘,降低了终端设备与MEC服务器[2-3]间的通信距离,进而降低了时延和能耗。此外,将MEC服务器与基站(base station, BS)相结合可提高网络吞吐量。

因移动方便、易部署、构建灵活,将UAV作为空中基站进行信息传输属UAV的典型应用[4]。在该应用中,UAV为用户终端之间建立通信链路。而基于UAV辅助的MEC网络可依据终端需求,为终端提供计算服务。

文献[4]的研究表明,由MEC网络产生的上行链路的数据量是下行链路的5至10倍。为了有效处理上行链路中超大数据量问题,采用正交多址接入(non-orthogonal multiple access, NOMA)技术,提高频谱利用率。在上行的NOMA中,终端引用叠加编码,使多路信号能够在同一个频率信道上传输。BS端采用连续干扰消耗技术解码多路信号。

为此,提出基于UAV的移动边缘计算的最小化能耗算法(energy consumption minimization algorithm, ECMA)。在该场景中,UAV作为MEC,帮助终端完成计算任务。主要工作包含:1)构建关于时隙分配、任务分配和UAV移动轨迹的能耗最小化的目标问题;2)采用“分而治之”策略求解目标问题,并分别引用迭代算法和连续凸近似法求解子问题。仿真结果表明,提出的ECMA算法降低了终端能耗。

1 系统模型及问题描述

1.1 网络模型

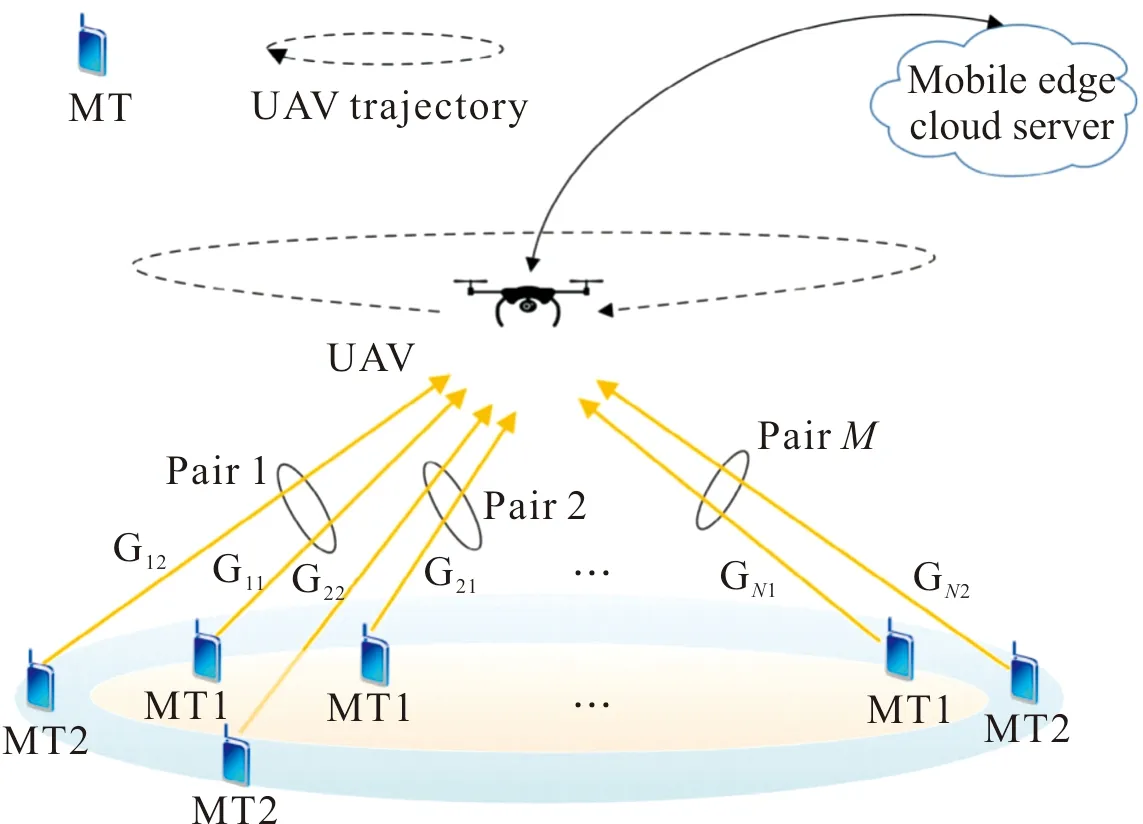
图1 网络模型Fig.1 Network model

假定M对MT均匀在分布于蜂窝区(Cell)内外。每一对MT只有一个MT位于Cell内,另一个位于Cell外。每对MT在相同的子载波上利用NOMA技术,同步向UAV传输数据。此外,不同对MT间利用时分多址接入技术(time division multiple access, TDMA)接入信道,如图2所示。

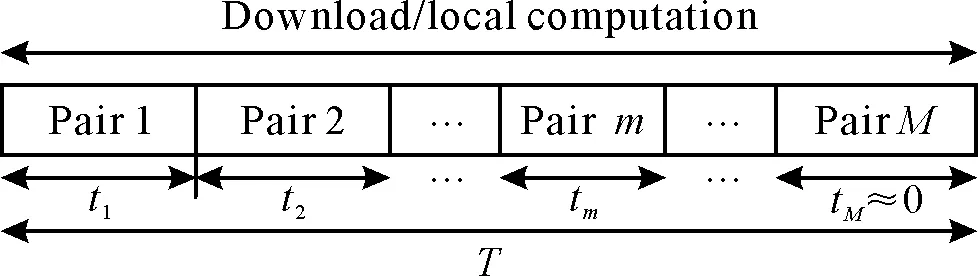
图2 时隙分配Fig.2 Time slot assignment

不失一般性,令Q0和QF分别表示UAV在每一轮数据收集阶段中移动轨迹的起点和终点。令T表示UAV收集M对MT数据所允许的收集时间(以下简称允许收集时间)。即UAV需在允许收集时间内收集M对MT传输的数据。将允许时间分成m个时隙。令tm表示第m个时隙的时长。假定在每个时隙内,UAV是静态的,即它在空中盘旋为某一对MT进行服务。

1.2 基于视距链路的信道模型

由于UAV位于高空,将UAV与MT间的链路视为视距链路。在时隙tm,第m对MT(两个MT分别标记为MT1和MT2)与UAV间的信道增益为[4]:

(1)

(2)

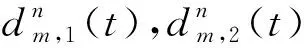
2 问题描述

文中从任务分配、时隙分配和UAV移动轨迹三方面降低网络的能耗。为此,先建立能耗最小化的目标问题,再进行求解。

2.1 任务卸载模型

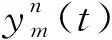
(3)

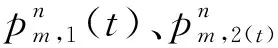
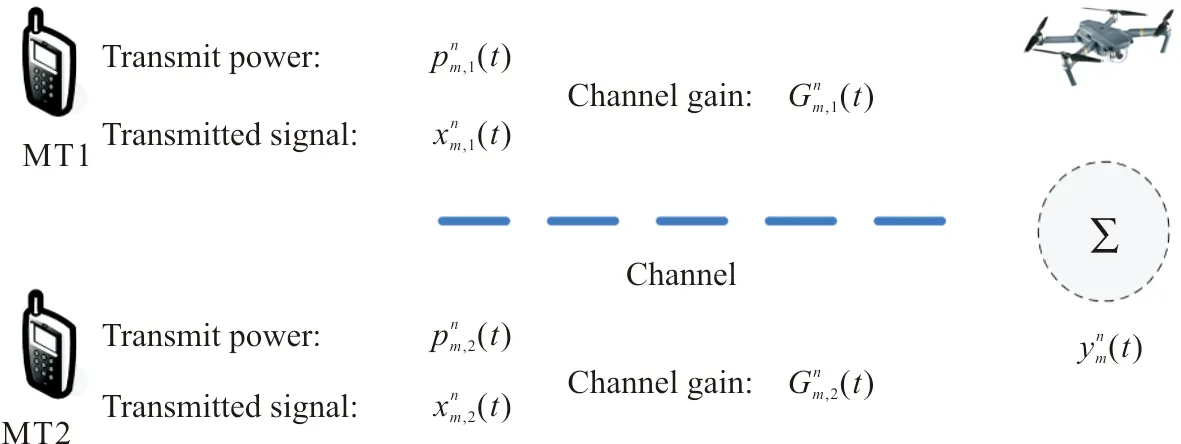
图3 第m对MT向UAV传输信号示意图Fig.3 Schematic diagram of MT the mth pair of transmit signal toward UAV

UAV分别从MT1和MT2所获取的卸载任务率为[5-6]:

(4)

式中σ2表示噪声功率。

由于给MT1和MT2分配的时隙是tm,它们在tm时间内所产生的数据量为:

(5)

将式(4)代入式(5),整理可得:

(6)

式中:αm,1=σ2/Gm,1;αm,2=σ2/Gm,2。

2.2 UAV的移动和能耗

ECMA算法采用旋翼无人机实现。无人机依据轨迹进行移动,即从起点Q0移动至终点QF。令ϑmax表示无人机最大的移动速度。它在移动过程中满足以下约束条件[7-10]:

(7)

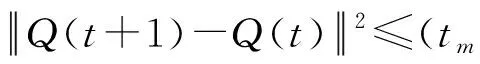
(8)

式中:Q(1),Q(t+1)分别表示UAV的初始位置和在时刻(t+1)的位置;Q0,QF分别表示UAV轨迹的起点、终点。

UAV在飞行阶段其旋翼所消耗的功率为:

(9)

式中:p0和pi分别表示无人机在盘旋状态时叶片轮廓功率和诱导功率;Wtip表示旋转叶片的端速;υ0表示旋翼诱导速度;d0表示机身阻力比;ρ表示空气密度;A表示旋转盘区面积;s表示旋转固体密度。

然后,依据式(10)计算UAV的速度:

(10)

因此,UAV在飞行期间,共消耗的能量为:

(11)

2.3 任务计算模型

(12)

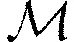
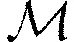
(13)

(14)

UAV作为边缘计算服务器,存在计算容量限制。令S表示边缘计算服务器的计算容量。因此,所有用户所上传的数据量应满足以下约束条件:

(15)

2.4 能耗模型

(16)

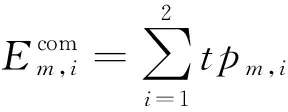
2.5 问题描述

ECMA算法从任务分配、时隙调度和UAV的轨迹三方面降低用户的能耗。因此,构建如式(17)所示的形式化问题:

(17)

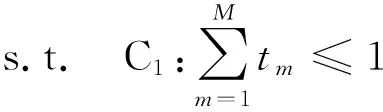
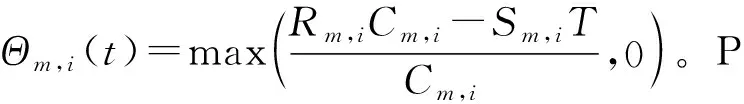
3 基于“分而治之”策略的求解

由于C1,C4和C7为不等式,P问题为非凸问题。因此,采用传统方法直接求解P问题相当困难。为此,将P问题拆分成P1,P2两个子问题:P1为时隙调度和任务计算分配;P2为UAV轨迹优化。

3.1 P1问题

本小节讨论P1问题。P1问题是:在UAV采用固定轨迹以及传输功率为常数的条件下,如何优化时隙分配和任务计算分配。P1问题的形式化表述如式(18)所示:

(18)

s.t. C1,C2,C3,C4

由于式(18)的约束条件是线性的,很容易证明P1问题是凸问题(证明过程可参照文献[9])。然而,尽管P1问题是凸问题,但是直接求解P1仍较复杂。为此,将P1问题进一步拆分成P1-1,P1-2两个子问题:P1-1为时隙分配;P1-2为任务计算分配。

3.1.1 P1-1问题

P1-1问题是在θ为常数条件下求解tm的问题。为此,在θ为常数的前提条件下,将式(18)问题写成拉格朗日函数形式L1:

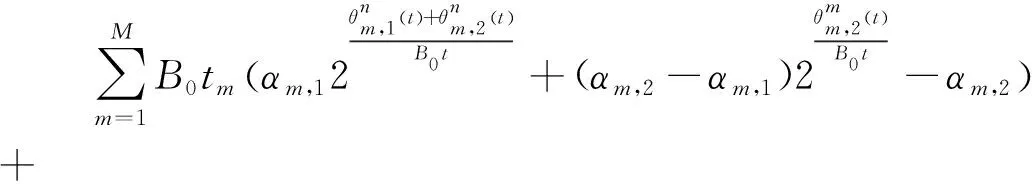
(19)

式中:μ表示非负的拉格朗日乘子。

对L1求一阶导数:

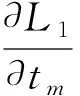
(20)

式中:

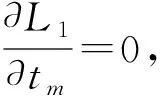
(21)

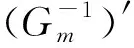
3.1.2 P1-2问题

P1-2问题是在tm为常数条件下求解θ问题。为此,在tm为常数的前提条件下,将式(18)问题写成拉格朗日函数形式L2:

(22)

式中:ρ为非负的拉格朗日乘子。

对L2求一阶导数:

(23)

(24)

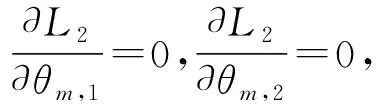
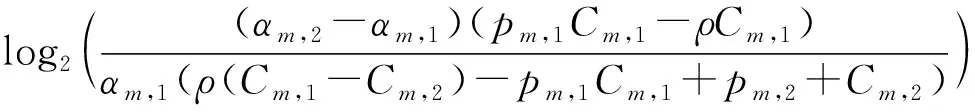
(25)

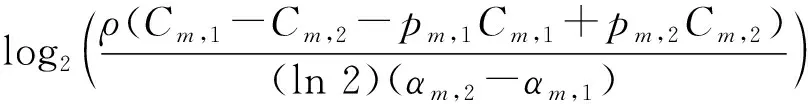
(26)

3.2 P2问题

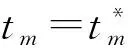
(27)

s.t. C5,C6,C7,C8

式(27)的优化问题为非凸问题。采用连续凸近似(successive convex approximation, SCA)算法求解此问题。作为求解非凸问题的处理方法,SCA算法将非凸问题转化凸问题,进而得到原问题的近似解。

4 性能分析

4.1 仿真环境

将UAV放置在高度为100 m的空中,其最大移动速度υmax为25 m/s。具体的仿真参数如表1所示[11]。此外,考虑的路径衰落模型为:128.1+37.61lgd,其中d的单位为km;网络带宽B0为10 MHz;噪声功率密度σ2为-115 dBm/Hz[11]。

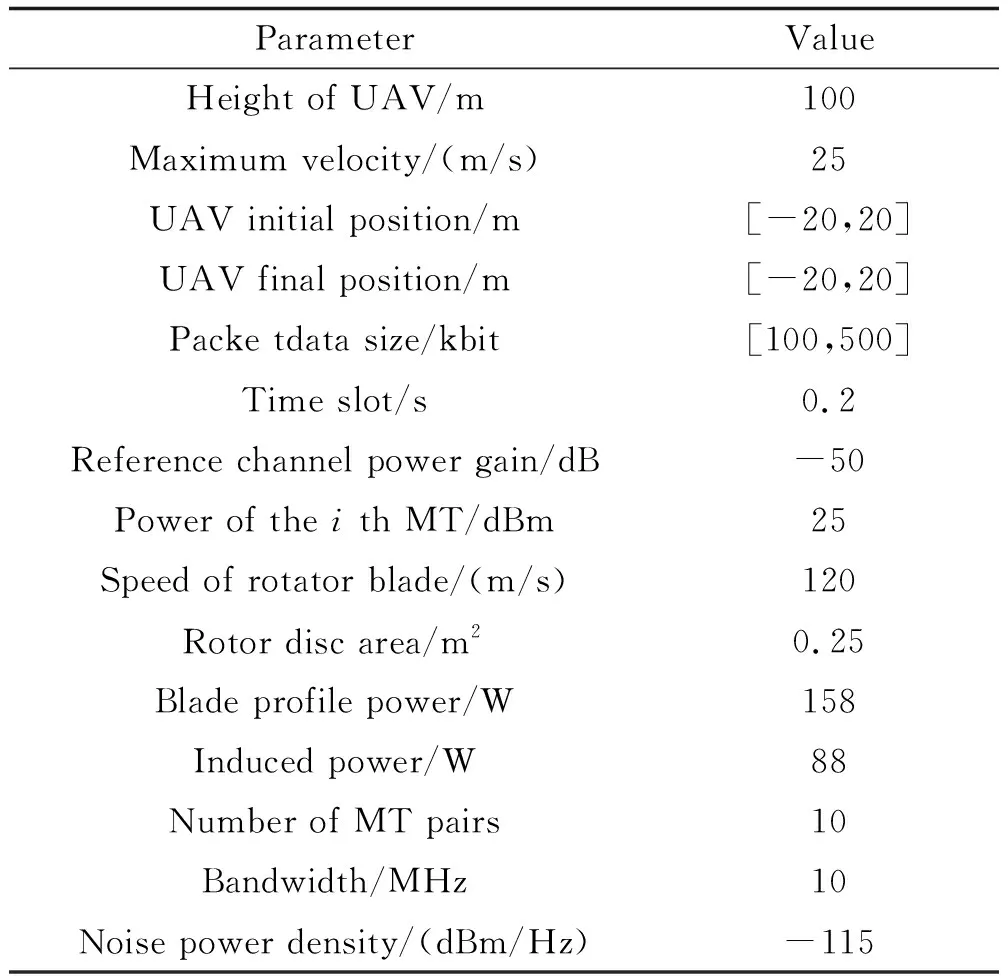
表1 仿真参数Table 1 Simulation parameters

此外,为了更好地分析ECMA的抑制能耗性能,选择正交多址接入算法(orthogonal multiple access algorithm, OMAA)[7]和等功率分配算法(equal power allocation algorithm, EPAA)[12]作为参照,并对比分析它们的能量消耗性能。OMAA算法中UAV不采用NOMA技术,而是采用正交多址接入技术;EPAA算法不对UAV的功率进行优化,而是采用等功率,即UAV采用等功率向M对MT传输数据。

4.2 边缘服务器计算容量对能量消耗的影响

首先分析边缘服务器计算容量S对能量消耗的影响,如图4所示。从图可知,服务器计算容量值越大,终端所消耗的总能量越小。原因在于:服务计算容量越大,允许终端向UAV上传的数据量越多,留给终端自己计算的任务量越少,这就降低了终端能耗。

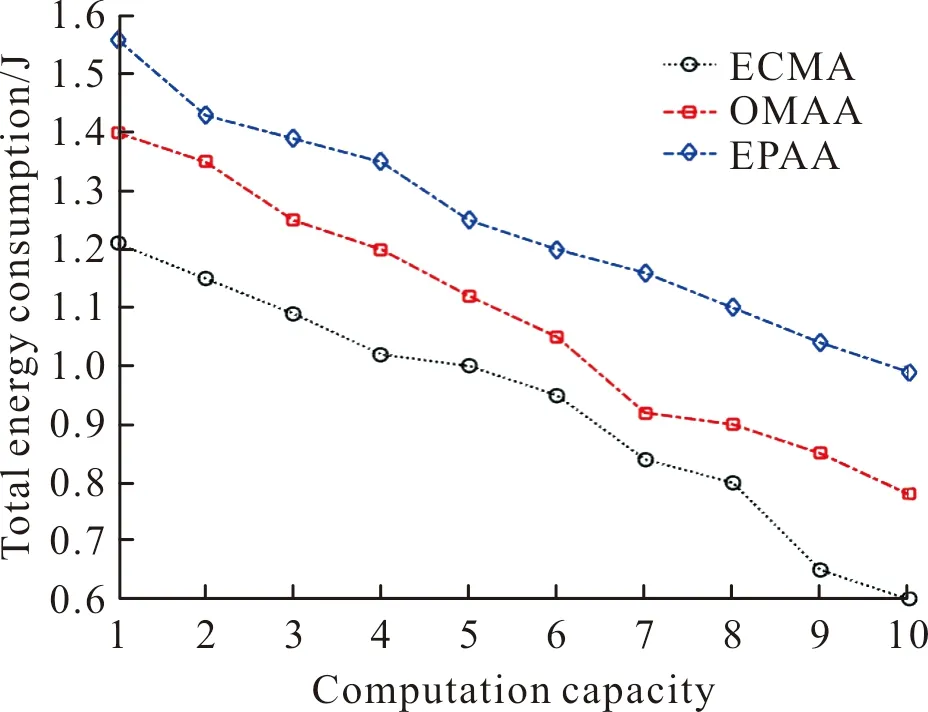
图4 服务器计算容量S对能量消耗的影响Fig.4 The impact of computation capacity on energy consumption

此外,相比于OMAA和EPAA,提出的ECMA算法的能耗平均分别下降了约16.66%和33.33%。原因在于:ECMA算法通过时隙分配、任务分配和UAV轨迹三方面降低了ECMA算法的能耗。

4.3 允许接收时间对能量消耗的影响

接下来,分析允许接收时间T对终端能耗的影响,其中T从6～30 s变化,如图5所示。

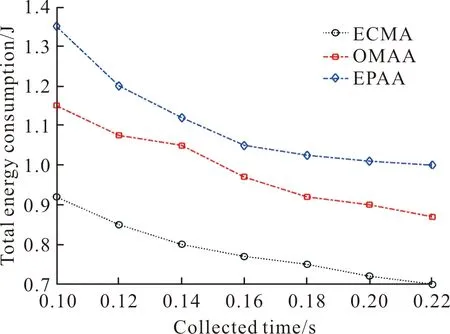
图5 允许收集时间对能量消耗的影响Fig.5 Collected time on energy consumption

从图可知,延长T值有利于减少终端所消耗的能量。原因在于:若T变长,则有更多充足时间传输数据,就可降低传输功率,这有利于减少终端在通信阶段所消耗的能量。此外,相比于OMAA和EPAA,ECMA算法在能耗方面的性能仍存在较大优势。

4.4 MT对数对能量消耗的影响

MT对数从1～10变化对能耗的影响如图6所示。从图6可知,终端总能耗随MT的对数呈线性增长关系,这符合逻辑。MT的对数越多,终端数越多,所消耗的能量就越多。此外,相比于OMAA算法、EPAA算法,ECMA算法降低了能量消耗。原因在于:ECMA算法对计算任务和时隙分配、UAV轨迹进行了联合优化。同时,ECMA算法采用NOMA接入技术,降低了彼此干扰,这也有利于减少能量消耗。

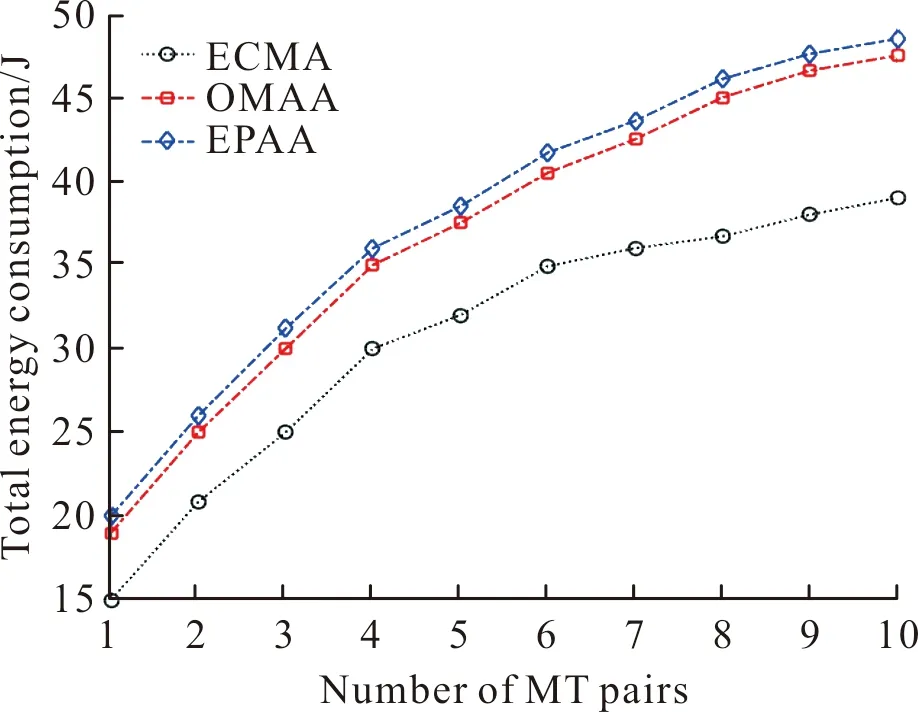
图6 MT对数对能量消耗的影响Fig.6 Impact of number of MT pairs on energy consumption

5 总结

针对UAV和终端的能耗问题,提出基于UAV的移动边缘计算的最小化能耗算法ECMA。ECMA算法先建立能耗最小化的目标问题,再采用“分而治之”策略,将目标问题拆分为子问题,再求解,进而获取使网络能耗最小化的解。仿真结果表明,提出的ECMA算法有效地降低了网络能耗。为更好实用化,后期将研究非视距链路和多径衰落信道对ECMA算法能耗的影响,进而对ECMA算法进行改进。