成像制导巡飞弹无源目标定位与误差分析

凡建超，鱼小军，周建军，张飞飞，李 格

(湖南云箭集团有限公司，湖南 长沙 410100)

0 引言

巡飞弹是飞航导弹的重要发展分支,既可在指定区域上空长时间盘旋飞行,并对目标区域进行侦察、监视,又可携带战斗部及时摧毁目标。典型产品有美国的快看(Quicklook)巡飞弹和俄罗斯的R-90巡飞子弹药等[1]。

巡飞弹的目标定位按工作机制可以分为有源定位[2]和无源定位[3-5]。有源定位以基于姿态/激光测距定位模型为主,该模式下,目标定位精度较高,但是需要配备激光测距机,这对巡飞弹的体积和重量要求苛刻,并且成本较高;无源目标定位无需主动发射辐射源,隐蔽性强,可通过摄像机采集目标图像,利用图像分析法获取目标的位置。

目前对目标定位原理的研究主要为运动学分析,集中在空间坐标变换的描述方法上。Algrain[6]推导了机载三轴红外阵扫描机构的目标定位和指向算法,用于雷区探测和识别。Skoglar[7]采用 Denavit-Hartenberg方法分析了机载光电侦察系统在目标定位过程中的前向和后向运动学方程。Poisel[8]系统研究了电子战中的各种目标定位算法,如基于梯度下降法、三角测量法和时间参数法等。Spingarm[9]研究了利用扩展卡尔曼滤波技术在移动载体平台上对目标进行定位的问题。Fu[10]设计了基于LOB扇面的定位法,利用多个LOB扇面的重叠区域进行目标定位,使用光电探测系统的最大估计误差值以确保目标落在重叠区域内。同时,刘晶红[11]、李晓光[12]、张华海[13]、毛昭军[14]等国内学者均采用齐次坐标表示法,对机载光电探测系统的目标定位模型及其空间坐标转换关系进行了推导,得到了适用于机载光电探测系统的目标定位模型。

文中提出一种无源目标定位算法,通过成像导引头跟踪目标测量的框架角得到目标视线角的测量值;然后根据组合导航的巡飞弹位置、姿态角,及目标位置,建立目标定位系统的测量方程,利用推广卡尔曼滤波,估计出目标的位置,仿真结果表明:该方法定位精度高,应用范围广,具有较大的工程应用价值。

1 目标定位方案

1.1 目标视线角的量测值

在巡飞弹对地面目标定位的过程中,成像导引头通过伺服机构调整导引头的高低框架角与航向框架角,保证目标成像处于探测器中心,完成对目标识别与稳定跟踪[15-17]。

如图1所示,高低框架角φα为光轴指向在弹体系XOZ面的投影与光轴的夹角,目标在上方定义为正;航向框架角φβ为光轴指向在弹体系XOZ面的投影与弹体系OX轴的夹角,目标在左侧定义为正。

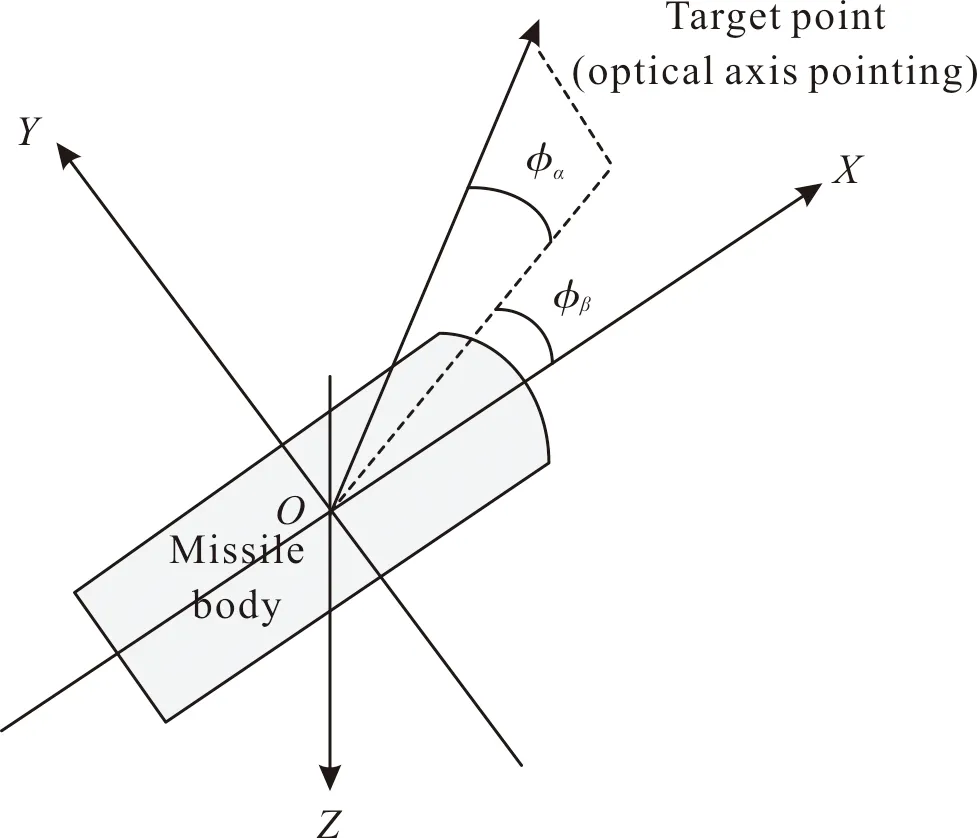
图1 导引头框架角示意图Fig.1 Schematic diagram of seeker frame angle

(1)

则沿目标视线的单位矢量xs1,ys1,zs1在弹体坐标系中的分量为:

(2)

弹体坐标系中目标-导弹相对位置关系如图2所示。图中θs,φs分别为弹体系目标视线高低角和目标视线方位角。

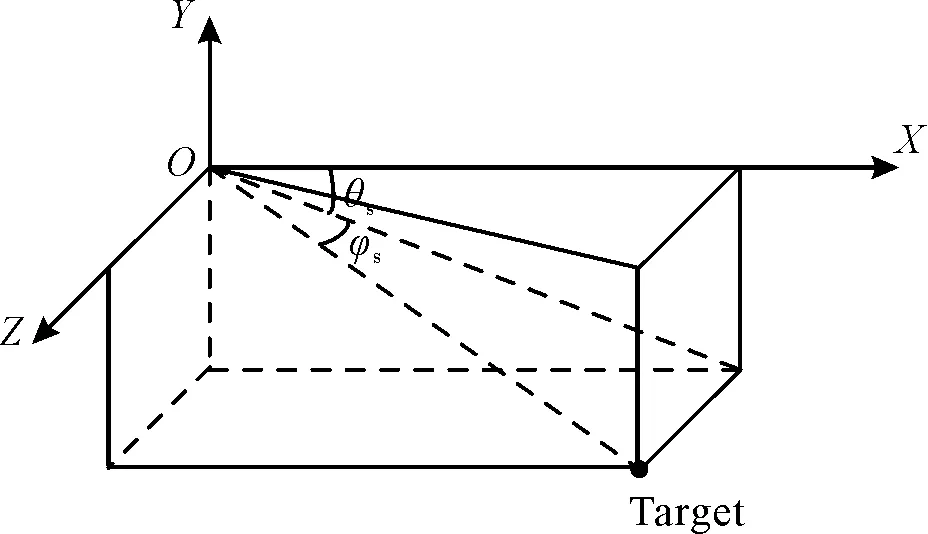
图2 目标-导弹相对运动关系示意图Fig.2 Schematic diagram of target-missile relative motion relation

则弹体系目标视线角的测量值为:

(3)

1.2 状态方程

选取发射系的目标位置为状态变量:

X=[x1x2x3]T=[xgtygtzgt]T

(4)

其中xgt,ygt,zgt为目标在发射系下的坐标。建立状态方程为:

X(k+1)=Φ(k+1|k)X(k)

(5)

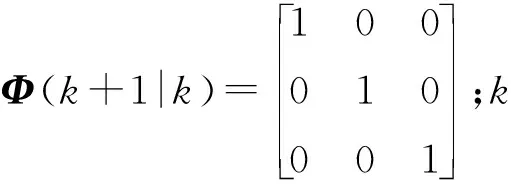
1.3 测量方程

巡飞弹在对目标定位的过程中,导航系统持续对弹的位置及姿态进行测量,导引头对目标进行稳定跟踪,据此信息可建立系统的测量方程。发射系到弹体系的转换矩阵为:

(6)

其中γ,ψ,φ为弹体系与发射系相互转换的滚转角、偏航角与俯仰角。

由此可得目标-巡飞弹发射惯性系相对距离矢量在弹体坐标系中的投影为:

(7)

式中xgm,ygm,zgm为巡飞弹在发射系下的坐标。

则弹体系下的目标视线高低角和目标视线方位角的真值为:

(8)

k时刻成像导引头测量的弹体系目标视线角为:

(9)

以成像导引头测量的弹体系目标视线角作为被动定位系统的观测量,建立观测方程为:

Z(k)=h(X(k))+v(k)

(10)

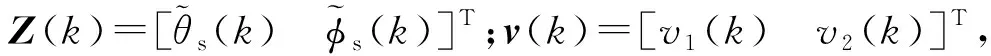
(11)

2 基于EKF的目标定位算法

根据式(5)、式(10)建立的系统状态方程和观测方程,目标定位问题演变成多次观测求最优估计值的问题。对于弹体系目标视线角,有两种方法可以得到:1)根据成像导引头高低框架角与航向框架角测量值,由式(3)得到;2)根据巡飞弹的位置坐标及目标位置的估计值,结合弹体姿态角,由式(11)得到。对于这一类最优估计问题,常用的方法有极大似然估计法(MLE)、最小二乘估计法(LSE)、推广卡尔曼滤波算法(EKF)进行处理。在非线性系统中,常用推广卡尔曼滤波算法(EKF)进行处理,该方法的核心思想是,对一般的非线性系统,首先围绕滤波值将非线性函数展开成Taylor级数并略去二阶及以上项,得到一个线性化模型,然后启用卡尔曼滤波[18]完成对目标的滤波估计等处理。具体方法如下:

由被动定位系统数学模型可知,系统状态方程为线性方程,测量方程为非线性方程,形式为:

(12)

式中:X(k)为3×1维状态向量;Z(k)为2×1维观测向量;h(·)为量测阵,是2×1维可微向量函数;v(k)为量测噪声序列,是2×1维高斯白噪声。

统计特性为:E(v(k))=0,E(v(k)vT(j))R(k)。其中,E(v(k))为求v(k)的平均值,R(k)为量测噪声序列的方差阵。

定义:

(13)

则对于被动定位系统的测量方程H(k+1)为:

(14)

推广卡尔曼滤波算法(EKF)可写为:

(15)

初值选取:X(0/0)=E(X(0))=X0,P(0/0)=σ(X(0))=P0。其中E(X(0))为求X(0)的均值,σ(X(0))为求X(0)的方差阵。

采用推广卡尔曼滤波算法,可以得到目标位置的最优估值。

3 仿真结果与误差分析

3.1 仿真结果

通过Matlab的Simulink数学工具,建立巡飞弹六自由度数学仿真模型,针对某一典型弹道,采集巡飞弹稳定跟踪某一固定目标的过程中导引头的框架角信息、巡飞弹的位置信息、姿态角信息,通过推广卡尔曼滤波算法验证对目标定位的有效性。

仿真条件:巡飞弹投放高度为10 000 m,投放速度为240 km/h;目标位置坐标为[15 000 m,-17.7 m,0 m],巡飞弹位置测量精度均为10 m(1σ),姿态角测量精度均为0.3°(1σ),导引头框架角测量精度均为0.2°(1σ)。

仿真结果曲线见图3～图5。

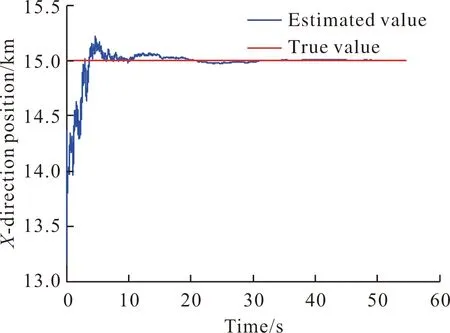
图3 目标X向位置定位估计值Fig.3 X-direction positioning estimation value of target

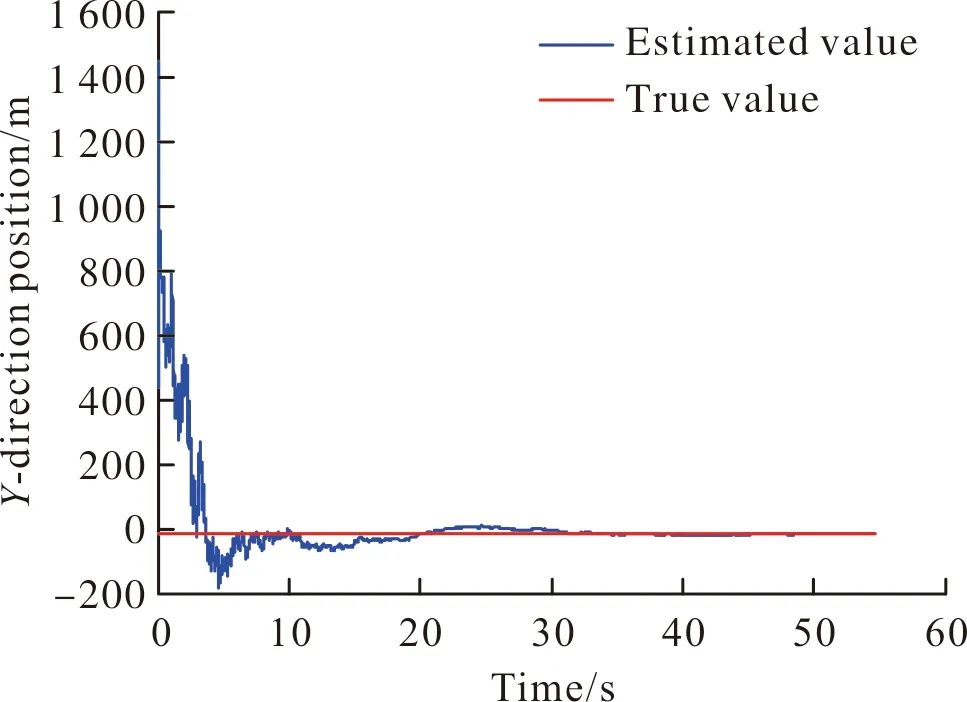
图4 目标Y向位置定位估计值Fig.4 Y-direction positioning estimation value of target

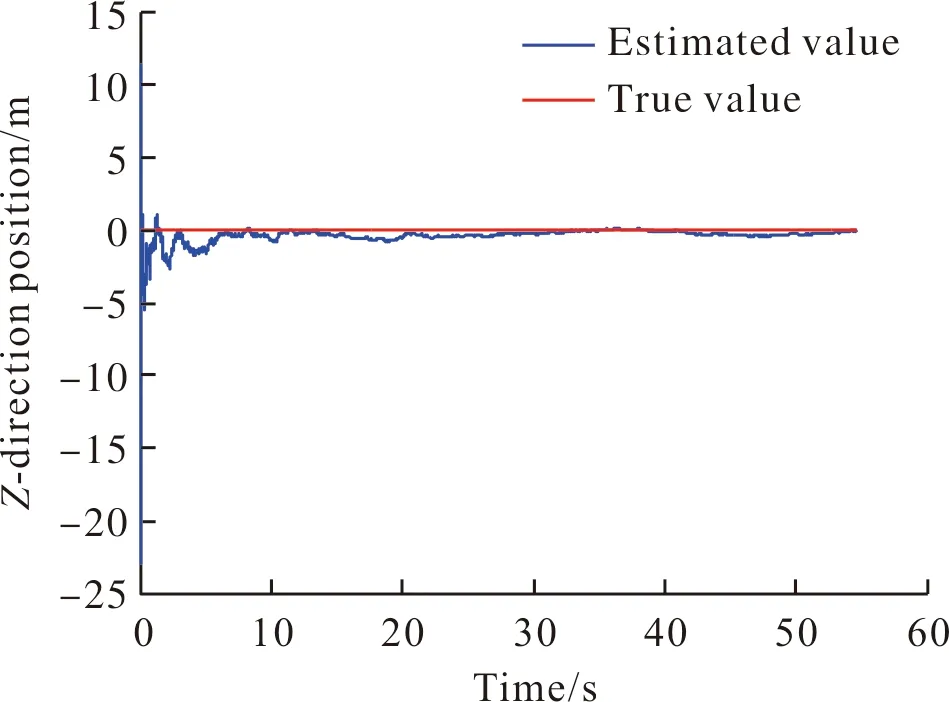
图5 目标Z向位置定位估计值Fig.5 Z-direction positioning estimation value of target

由仿真结果可知,巡飞弹在稳定跟踪目标后,对目标进行定位估算,在15 s时刻,目标定位X向位置定位为15 035.0 m,Y向位置定位为-44.9 m,Z向位置定位为0.05 m;在弹道末端,目标定位X向位置定位为14 996.0 m,Y向位置定位为-14.5 m,Z向位置定位为-0.04 m。测量数据的误差影响系统的定位精度,相关初值的选择影响系统的收敛的快速性。在约15 s的时间内,就可达到相当高的定位精度;且飞行时间越长,定位精度越高。

3.2 误差分析

3.2.1 误差源

根据式(1)～式(11),目标定位误差与巡飞弹的位置定位精度、姿态角的测量精度、导引头框架角的测量精度有关,可定义目标定位误差分析模型:

(16)

式中:Δx、Δy、Δz分别表示目标的X向、Y向、Z向位置误差;f(xgm,ygm,zgm)表示巡飞弹位置精度对定位精度的影响;g(φ,ψ,γ)表示姿态测量精度对定位精度的影响;l(φα,φβ)表示导引头框架角测量精度对定位精度的影响。

3.2.2 蒙特卡洛统计分析

使用蒙特卡洛方法分析和计算目标定位误差[19]。首先根据导航系统和成像导引头测量误差分布特性,确定巡飞弹位置的测量误差、姿态角的测量误差、导引头测量误差服从表1所列的随机分布,通过对测量参数误差进行随机抽样处理,计算出目标位置坐标并统计定位误差。

表1 随机误差分布表Table 1 Random error distribution table

误差分析基本步骤为:

1)根据误差计算模型确定变量参数与误差分布空间;

2)选择随机序列长度(文中序列长度为1 000),根据误差分布,生成巡飞弹坐标位置随机参数、姿态角随机参数、导引头框架角随机参数;

4)分别计算目标位置的均值及标准差。

具体而言:

(17)

式中E(x),E(y),E(z)分别为目标定位统计结果的均值。

表2为巡飞弹坐标位置误差、姿态角误差、导引头框架角误差以及三者综合误差分别对目标位置定位精度的影响统计结果。

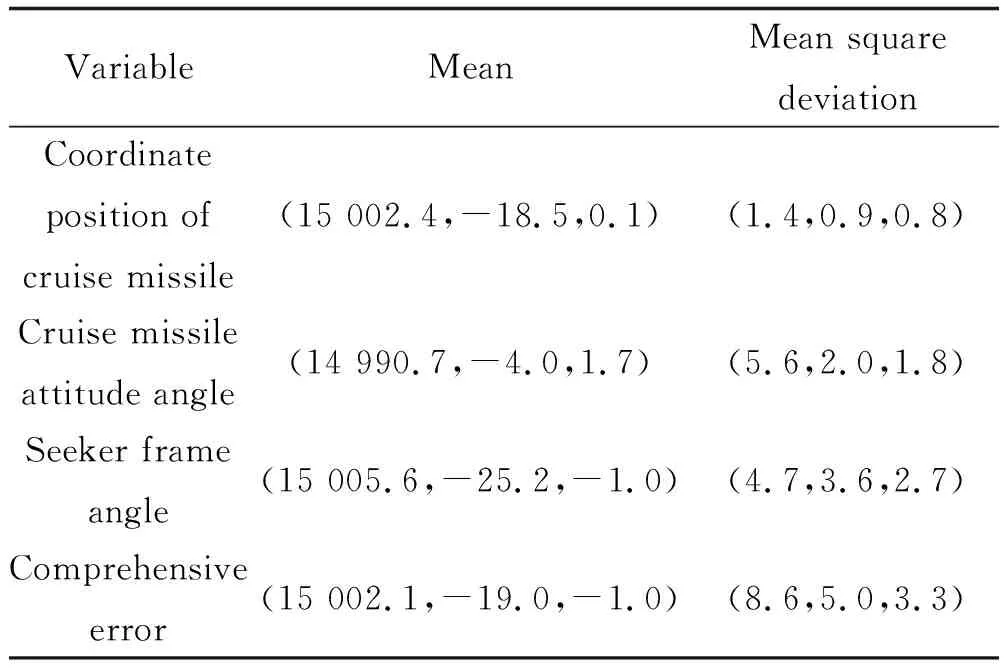
表2 目标位置误差统计结果Table 2 Statistical results of target positioning error m

由表2对目标坐标位置的统计的均值及误差可知,巡飞弹的位置精度对目标定位误差影响较小,导引头框架角测量误差及姿态角的测量误差对目标定位精度影响较大。针对目标定位精度的不同要求,则应选择相应精度的弹上陀螺仪及相应性能的导引头产品。

从巡飞弹坐标位置误差、姿态角误差、导引头框架角误差综合因素分析得到,目标定位误差CEP为10.9 m。

3.3 算法对比与优劣分析

文献[3]将一种无源目标定位算法应用于小型无人机,主要定位设备包括GPS接收机、惯性测量单元(IMU)、光电侦察平台(optoelectronic platform, OP),通过对同一目标点多次测量,进而建立目标定位的状态方程和测量方程,并利用无迹卡尔曼滤波算法估计目标位置。现将其所允许输入数据测量精度、中间计算过程和输出目标定位误差与文中结果进行简要比较分析,如表3所示。

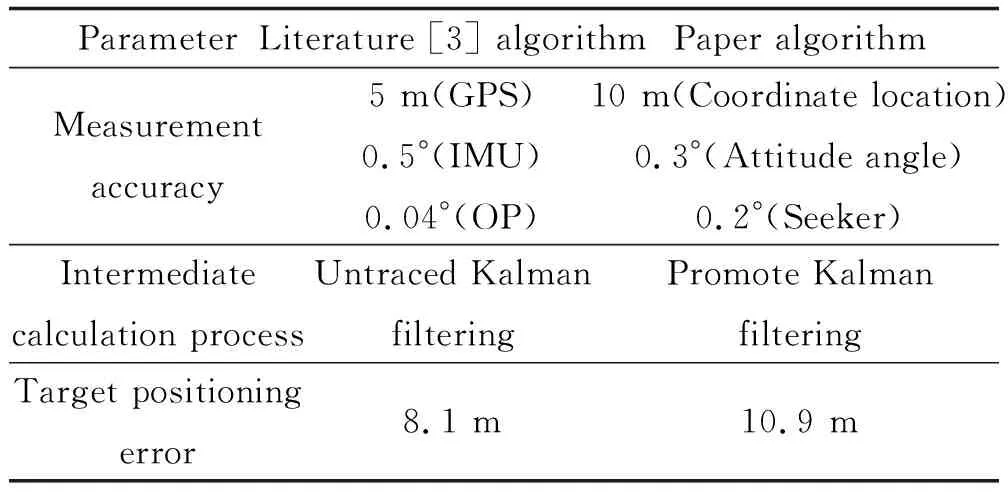
表3 算法对比Table 3 Algorithm comparison

从结果可以发现两种算法实现了较为接近的目标定位误差;文中所采用的导引头框架角测量精度劣于文献[3]光电侦察平台一个数量级的情况下,依然能够实现较为接近的目标定位误差。

从中间计算过程来看,文献[3]采用较为复杂的无迹卡尔曼滤波算法,该算法使用有限的样本点来近似描述非线性函数的概率分布,可知基于有限样本的概率分布与总体概率分布存在理论上不可避免的结构误差。为尽可能的得到非线性函数的总体概率分布,需要进行大数据量的样本采集,这一点对于飞行时间较短的巡飞弹难以实现。针对测量方程的非线性,文中采用的推广卡尔曼滤波算法,理论上具有良好的快速收敛性。

另外,与光电侦察平台相比,导引头产品价格更为低廉,易于实现巡飞弹的低成本化。

4 结论

由导引头框架角信息计算出弹体系目标视线角,作为系统的量测值;根据巡飞弹的坐标位置及姿态角,结合估算出的目标坐标位置,建立起系统状态方程与测量方程;然后通过推广卡尔曼滤波对目标位置可进行定位解算。由蒙特卡洛分析法统计出目标定位误差,通过仿真数据分析了测量参数误差与目标定位误差之间的关系,分析出对目标定位精度影响的关键因素,仿真结果表明文中方法不仅目标定位精度高,而且简单可行。