制导火箭INS辅助GNSS跟踪环路设计
王新龙,雷一非,赵 奇,吴 鹏
(西安现代控制技术研究所,陕西 西安 710065)
0 引言
制导火箭飞行弹道具有高动态运动的特点,传统独立式弹载全球导航卫星系统(GNSS)由于载体加速度突变,其载波跟踪环路相位误差容易迅速增大而造成跟踪环路失锁,且多普勒频率跟踪误差也容易迅速增大,带来较大定位误差[1]。为了能够稳定跟踪卫星信号,传统独立式弹载GNSS需要增加接收机的环路带宽,但是增加环路带宽又会加大环路噪声,降低环路的跟踪精度。对于进入跟踪环路的噪声来说,接收机跟踪环路带宽越窄则跟踪精度越高[2]。文中提出利用弹上INS辅助GNSS跟踪环路的方法来有效解决这个问题,采用一种INS辅助GNSS的2阶PLL跟踪算法,通过引入弹上INS估计的GNSS多普勒频率信息,采用外部辅助多普勒频率以及跟踪环路滤波器估计的残余多普勒频率,来控制跟踪环路中本地信号载波和码发生器,从而实现跟踪环路的闭合[3]。该方法可有效减小高动态对卫星信号跟踪稳定性的影响,提高制导火箭弹载GNSS跟踪环路的动态跟踪性能。
1 INS辅助GNSS跟踪环路设计
图1给出了INS辅助的2阶PLL载波跟踪环路结构。
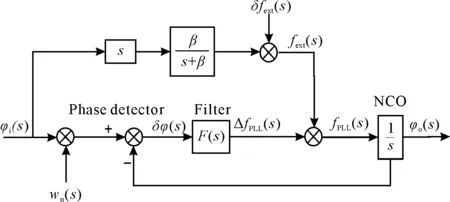
图1 INS辅助GNSS锁相环结构Fig.1 INS aided GNSS tracking loop
在图1中,φi(s)为接收到的卫星信号;wn(s)为随卫星信号进入环路的热噪声;F(s)为滤波器的传递函数,NCO为数控振荡器。增加的前馈支路为INS多普勒估计环节,微分环节s实现载波相位到载波频率的转换;低通滤波器β/(s+β)实现对INS估计环路的带宽限制,其中β为INS辅助估计的数据带宽;fext(s)为INS辅助得到的外部多普勒频率;δfext(s)为INS辅助的频率误差。
由图1可知,环路的输出相位为:
φo(s)=H1(s)φi(s)+H2(s)wn(s)+H3δfext(s)
(1)
式中:H1(s)=(βs+(s+β)F(s))/((s+β)(s+F(s)));H2(s)=(F(s))/(s+F(s));H3(s)=1/(s+F(s))。
由外部频率估计偏差造成的环路跟踪误差可以表示为:
δfPLL(s)=-H2(s)δfext(s)
(2)
由式(1)可知,当INS辅助的带宽β较大时,相位输出信号和参考输入信号呈线性关系,即用户接收机动态引起的相位绝大部分都可以由INS来跟踪。根据式(2)环路跟踪误差只和外部频率辅助偏差有关,即影响环路跟踪性能的只有导航滤波器估计的速度偏差和时钟偏差。因此,在设计INS辅助PLL跟踪环路时,对高动态环境特性要求较严的环路带宽完全可以由INS的环路辅助数据来补偿[4],此时影响环路带宽设计的主要因素有:导航滤波器估计的INS频率偏差、接收机的钟差和外部热噪声。
图2 给出了INS辅助的2阶PLL数字实现结构。具体实现过程为:卫星信号下变频采样数据完成载波剥离过程;然后根据INS估计的多普勒频率偏差和环路滤波的载波相位不断调整复制信号的参数,从而达到对输入信号的跟踪。其中,INS估计的多普勒频率主要用来抵消载体动态性能的影响,环路滤波的载波相位误差主要用来跟踪由热噪声、惯性器件和钟差引起的噪声误差。
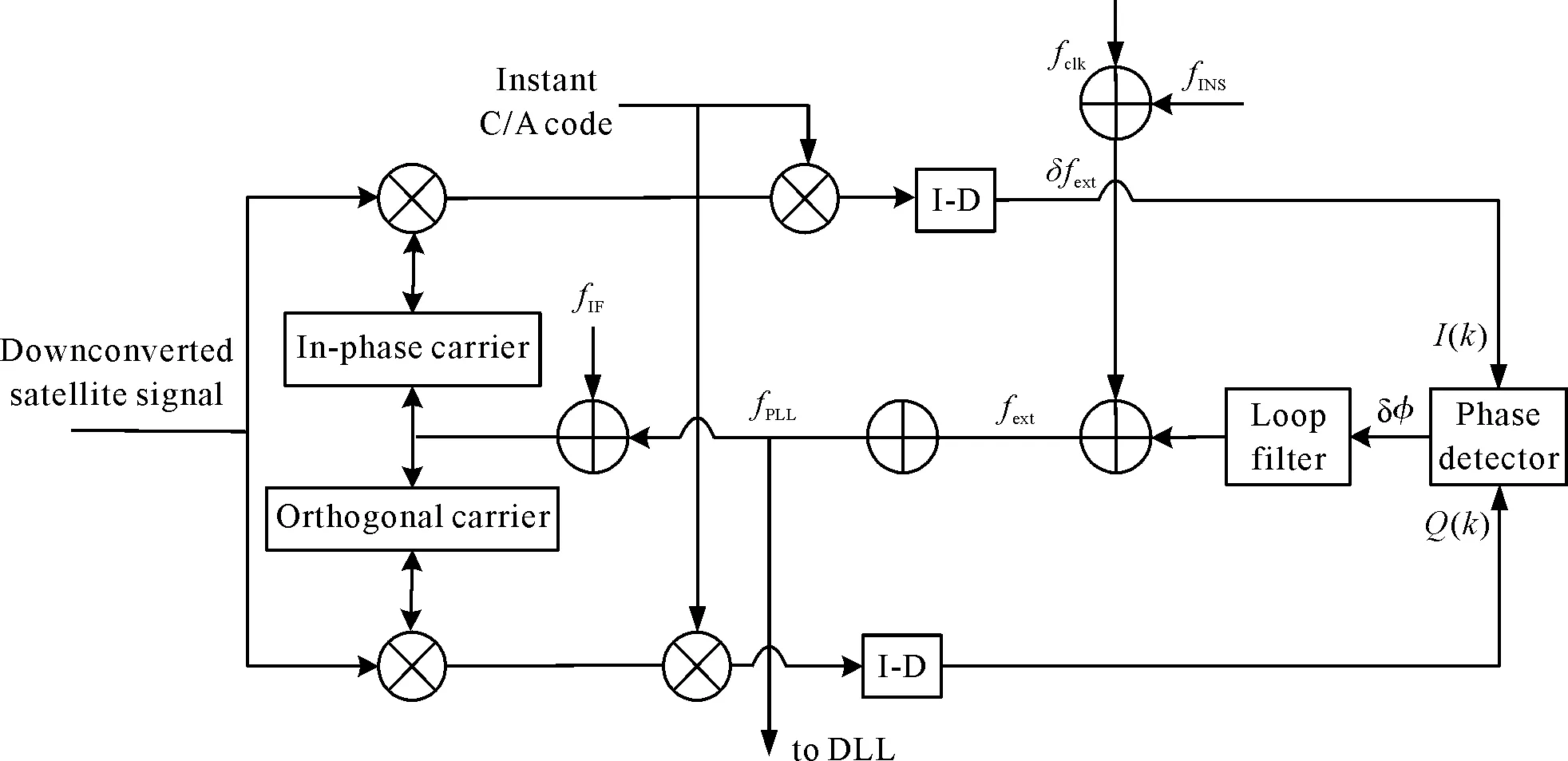
图2 INS辅助PLL数字实现结构Fig.2 Digital structure of INS assisted PLL
在INS辅助PLL数字结构中,同相和正交的载波信号为:
(3)
式中:fIF为载波中频频率;fINS为INS估计的多普勒频率偏差;tn=t0+nT,t0为初始时刻,T为积分时间间隔;φo为环路滤波输出的载波相位。
2 INS辅助PLL环路性能分析
2.1 误差模型建立
从闭环反馈控制系统的角度分析接收机PLL载波跟踪环。鉴相器用来求出接收到的卫星载波信号和本地复制的载波信号间的相位误差[5];环路滤波器采用低通滤波器对输出的估计值进行滤波处理,数控振荡器采用积分环节,对环路滤波器估计的本地载波频率进行积分调节,并达到对卫星信号跟踪的目的[6]。整个载波跟踪环路的s域模型如图3所示。
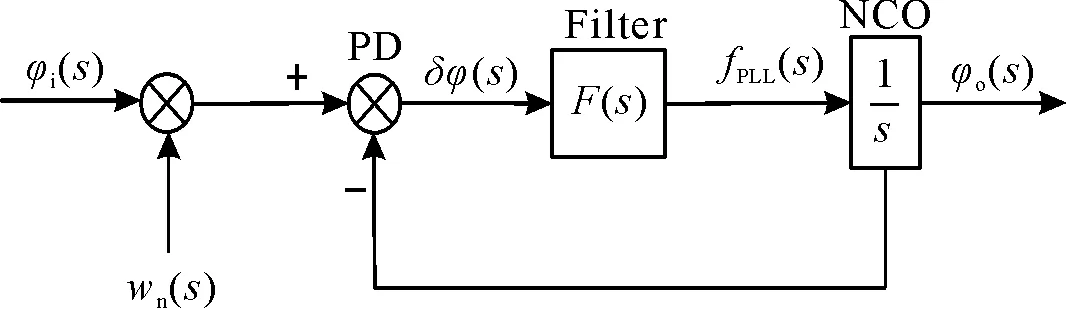
图3 载波跟踪环路的s域模型Fig.3 s-domain model of carrier tracking loop
图3中参数和图1中INS辅助GPS跟踪环路的含义相同,这里PLL环路滤波器为二阶环路,即
(4)
式中K,a为环路参数。
由此图3中系统的闭环传递函数可以表示为:
(5)
进而可求得系统的误差传递函数为:
(6)
当接收机处于高动态环境中,即有频率斜升信号θ(s)=AΔw/s3(A表示动态加速度大小)输入时,可求得跟踪环路的稳态相位误差为:
(7)
式中A为卫星和接收机视距方向上的等效载体加速度值的大小。
由此可知,当接收机处在高动态环境时,载波跟踪环路会产生相应的稳态误差。在加速运动条件下,将会产生恒定的跟踪误差;当接收机处于加速度运动条件下,稳态误差会进一步累计增大至载波跟踪环路失锁。
在图1所示的INS辅助GNSS载波跟踪环路中,由载体和卫星之间高速相对运动引起的多普勒频率偏移fdop可由INS测得的载体运动速度和接收机接收到的卫星星历计算得到:
(8)
式中:fT为发射信号的频率;fR为接收的信号频率;λc表示信号波长;(Vs-VR)表示卫星和接收机之间的相对运动速度矢量;e表示卫星和接收机视距方向上的单位方向向量。
为简化分析,假设理想状况下,忽略INS辅助的多普勒频率误差的影响,即
δfext(s)=0
(9)
分析加入INS辅助信息后对载波跟踪环路控制系统性能的影响,由于这时系统输入为输入信号φi(s)和随之进入系统的热噪声信号wn(s),因此可以从图1整个系统误差模型中得到:
(10)
(11)
同时可以得到整个系统对输入信号φi(s)的误差传递函数:
(12)
2.2 INS辅助PLL环路等效噪声带宽分析
一个实际可以运行的系统应该是稳定的,并且具有较好的动态性能。可通过环路的等效噪声带宽来分析INS辅助PLL跟踪环路的系统性能[7]。
当闭合环路频率响应为H(j2πf)时,环路通道的等效单边噪声带宽BL可表示为:
(13)
BL越小,即环路带宽越窄时,环路对输入噪声的抑制能力越强[8]。
当H(j2πf)=(cn-1(jΩ)n-1+cn-2(jΩ)n-2+…+c0)/(dn(jΩ)n+dn-1(jΩ)n-1+…+d0),n=1,2,3时,可分别求得积分结果为:
(14)
通过配置不同环路参数,可以得到不同的环路带宽,当取2阶PLL的最佳阻尼系数为0.707时,可得到不同参数下的理论等效环路带宽,如表1所示。
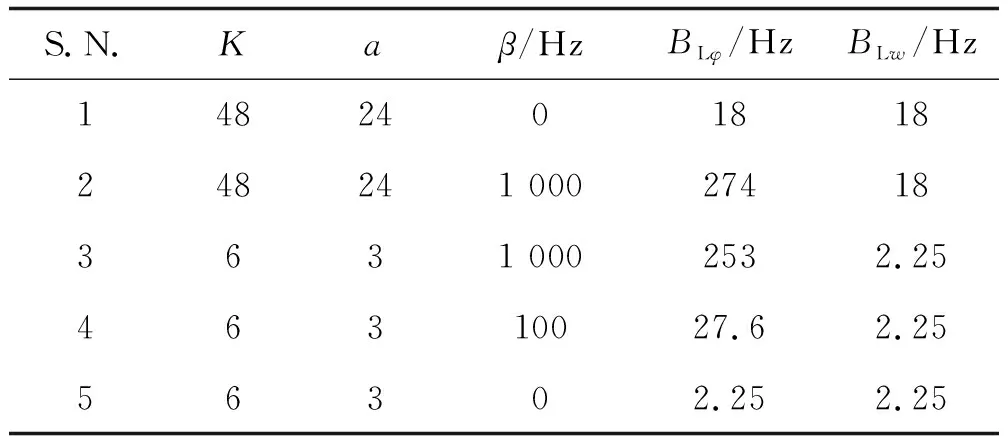
表1 等效理论环路噪声带宽Table 1 Equivalent theoretical loop noise bandwidth
表1中,BLw和BLφ分别表示输入热噪声的等效环路带宽和输入有用卫星信号的等效环路带宽,对比第2和第3组数据可以看出,环路参数K和a对输入卫星信号的等效环路带宽并无较大影响;由第4和第5组数据可以看出,当K和a的值不变,加入INS辅助环路数据带宽β为100 Hz时,输入卫星信号的环路带宽比相应的热噪声等效环路带宽大10倍以上,使卫星信号更容易被跟踪,因此采用INS辅助PLL载波跟踪环路结构的系统具有更好的动态性能。
3 INS辅助GNSS跟踪仿真实验
3.1 飞行轨迹参数设置和仿真参数选取
为评估高动态环境下INS辅助GNSS载波跟踪环路的跟踪性能,对二阶PLL和INS辅助二阶PLL的环路结构进行仿真,并分析其在高动态环境下的跟踪能力。
弹道参数并非真实参数,实际飞行过程中的空气动力学问题也未作考虑。图4是模拟的火箭弹经纬高三维立体飞行轨迹图。设置载体的飞行起始位置:纬度为39.98°N,经度为116.34°E,高度为1 300 m。
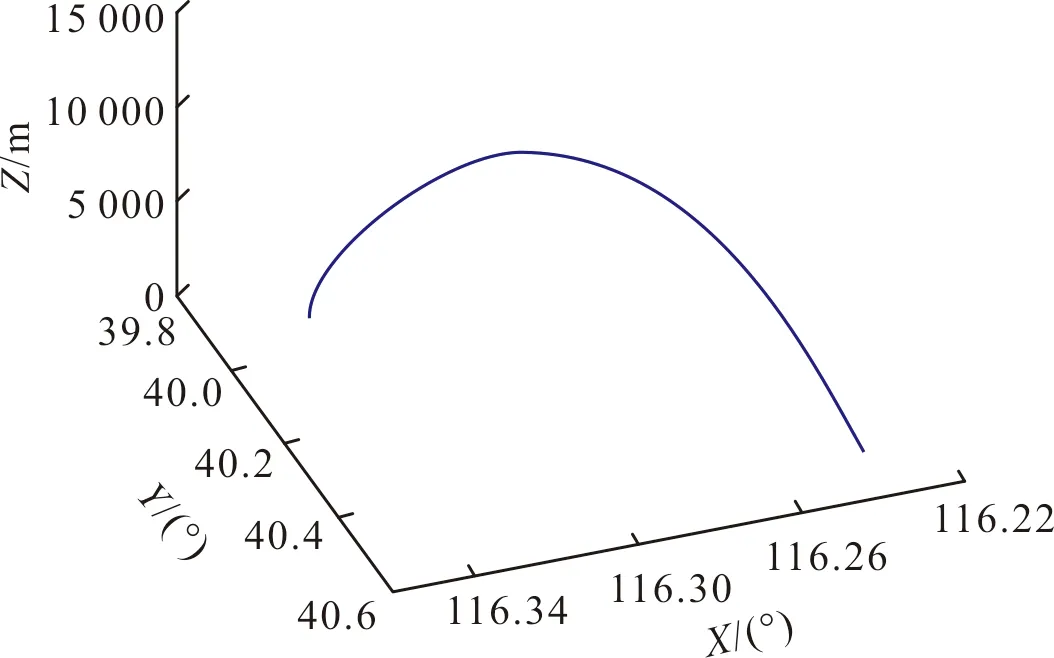
图4 理想火箭弹三维飞行轨迹图Fig.4 Ideal 3D flight trajectory map of rocket
3.2 IMU测量数据的产生
图5给出了载体飞行过程中的东向、北向和天向的飞行轨迹位置参数,图6是飞行过程中东北天方向上的加速度变化曲线图。
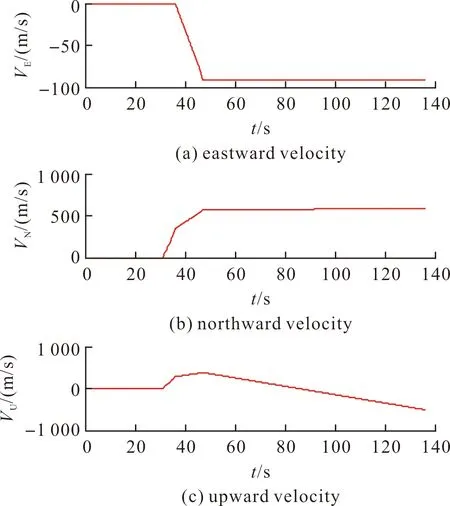
图5 飞行轨迹的三维方向速度Fig.5 3D velocity of flight path
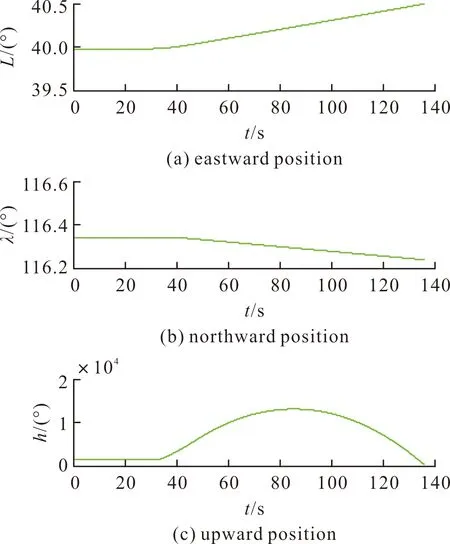
图6 飞行轨迹的三维方向位置Fig.6 3D position of flight path
根据轨迹参数和设定的加速度变化曲线图,可以反算出载体坐标系下的理论三轴加速度和三轴角速度[9]。考虑到实际飞行过程中IMU惯性装置测量精度问题,建立如表2所示的陀螺仪和加速度计误差模型,为简化分析误差模型仅考虑零位漂移、标度因数误差和随意游走误差3个主要误差源[10]。

表2 IMU误差模型Table 2 Error model of IMU
图7和图8分别为根据表2中IMU误差模型得到的三轴陀螺仪和加速度计的测量输出。
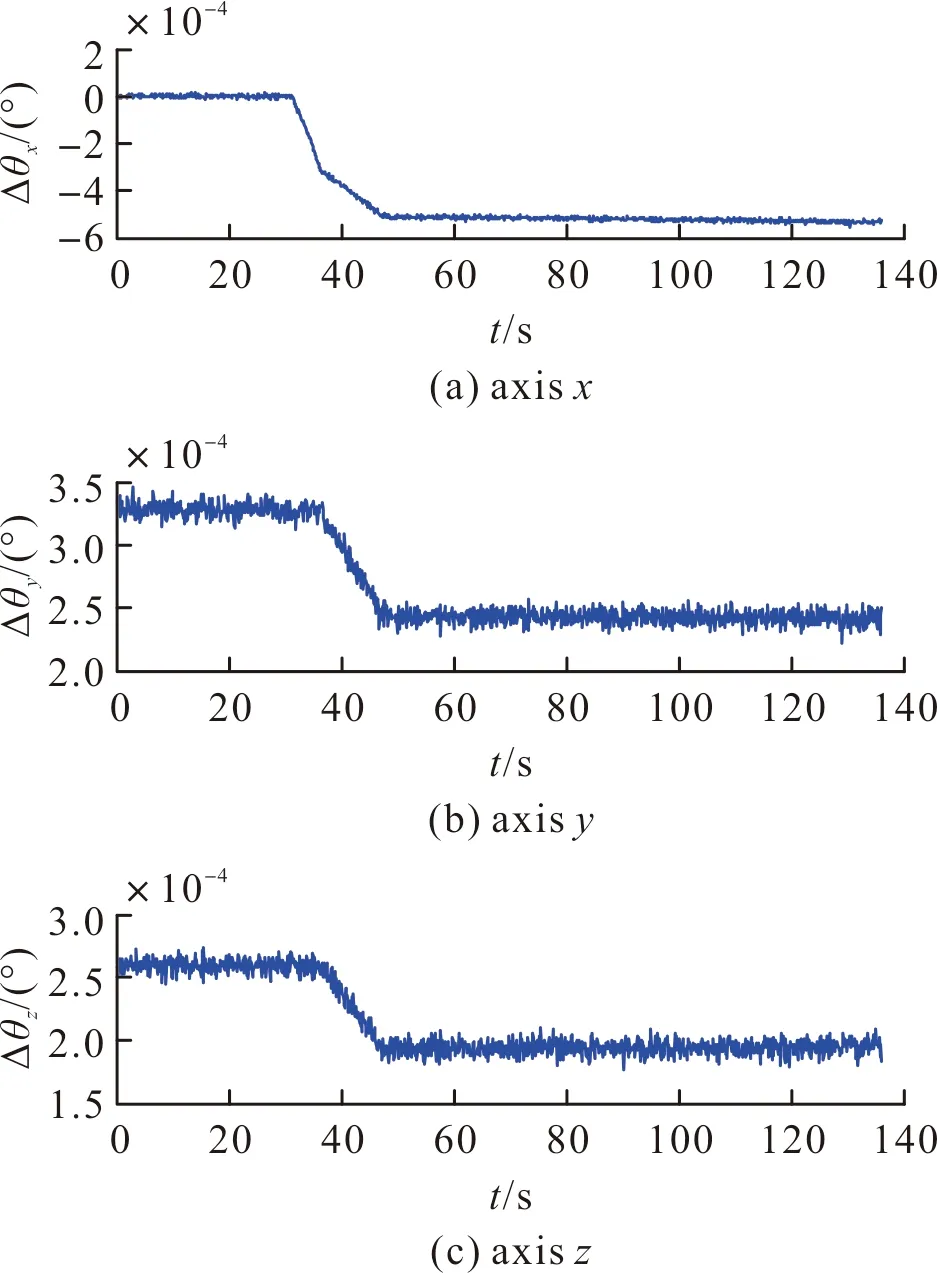
图7 IMU的三轴陀螺输出Fig.7 Three axis gyro actput of IMU
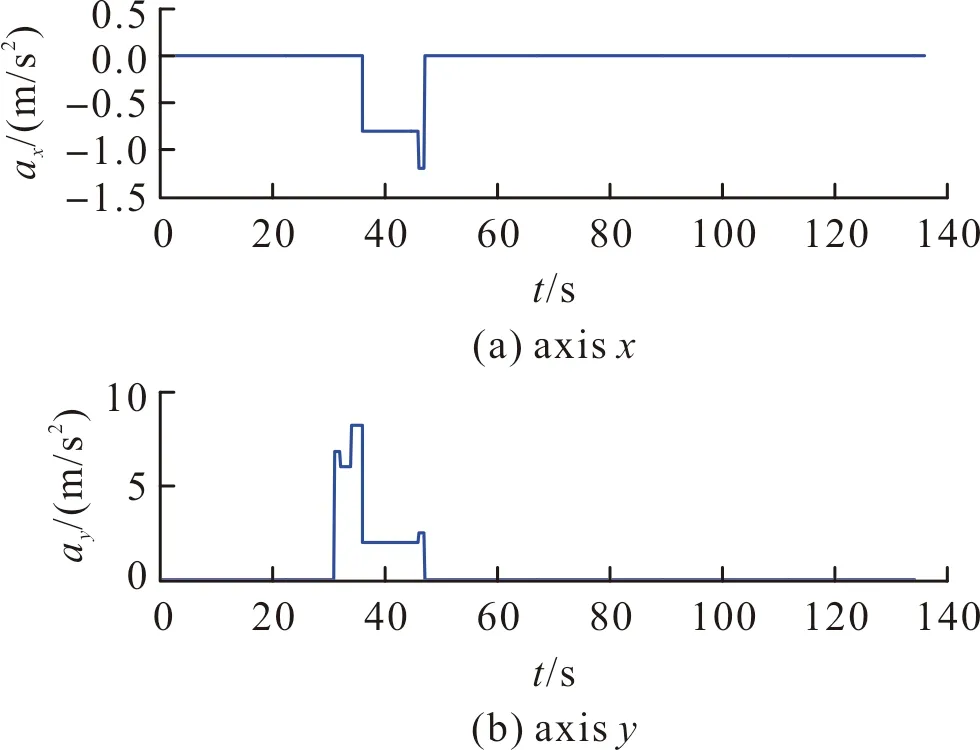
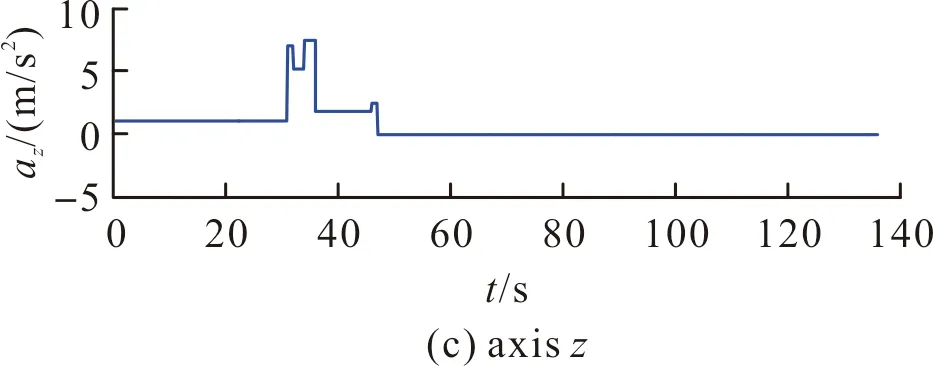
图8 IMU的三轴加速度输出Fig.8 Three axis acceleration output of IMU
3.3 卫星分布和数据采集
在卫星信号模拟器中设置载体接收机的起始位置为发射点位置:纬度39.98°N,经度116.34°E,高度1 300 m,使用5°的卫星信号遮蔽角(即观测卫星的仰角小于5°时将被剔除),同时设置接收机载体的运动轨迹和图5中所示的轨迹相同,可以得到某一设定时刻开始(图中设定初始时刻为2007-10-04 09:09:59),经过136 s载体运动的GNSS模拟卫星星历,GNSS模拟器设置界面如图9所示,其中上部地图为自动生成的。根据GNSS模拟器生成的原始星历文件就可以求解GNSS卫星在ECEF坐标系中的速度和位置信息[11]。
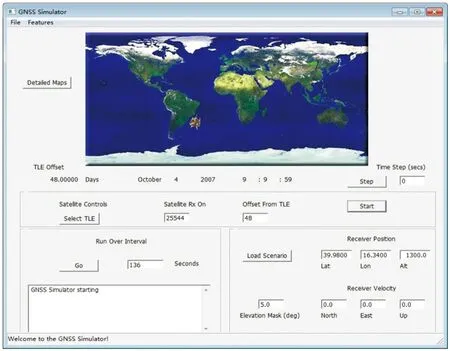
图9 GNSS模拟器设置参数图Fig.9 Parameters set by GNSS simulator
3.4 独立式GNSS和INS辅助GNSS跟踪性能对比
为对比高动态条件下独立式GNSS接收机和INS辅助GNSS接收机的跟踪性能,选取32~35 s的数据进行仿真试验,该时间段内载体的北向加速度由0突变到68 m/s2,天向加速度由8 m/s2突变到82 m/s2,给接收机环路稳定跟踪带来困难。设置预检测积分时间T=4 ms,PLL的跟踪带宽为18 Hz。图10和图11分别为独立2阶PLL跟踪环路和INS辅助2阶PLL跟踪环路在载体运动32~35 s过程中跟踪的载波相位误差。

图10 PLL2环路跟踪的相位误差Fig.10 Phase error of PLL2
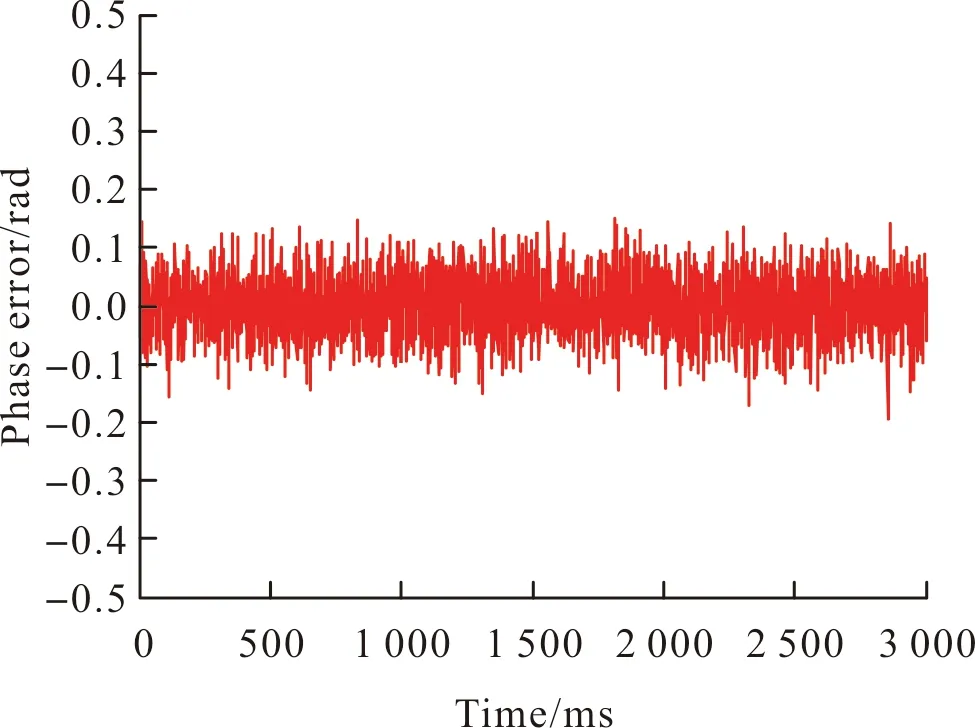
图11 INS辅助PLL2环路的相位误差Fig.11 Phase error of INS assisted PLL2
仿真结果表明:在该段时间内独立2阶PLL跟踪环路的相位误差已增大至±0.3 rad,而采用INS辅助2阶PLL跟踪环路的相位跟踪误差有效控制±0.1 rad范围内,采用INS辅助2阶PLL跟踪环路始终处在稳定跟踪状态。
该时间段内由于加速度的快速变化引起的动态应力会造成卫星和接收机视距方向上多普勒频移的迅速增加,给载波多普勒频率测量带来较大误差,图12和图13分别是独立2阶PLL和INS辅助2阶PLL跟踪10号星时测量的多普勒频率误差。
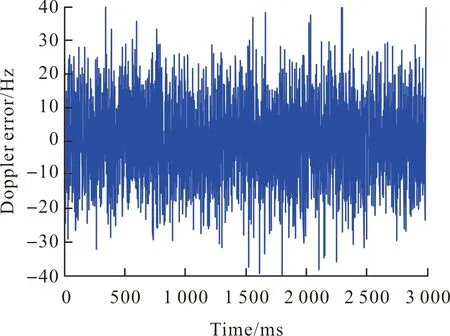
图12 PLL2环路的多普勒误差Fig.12 Dopple error of PLL2
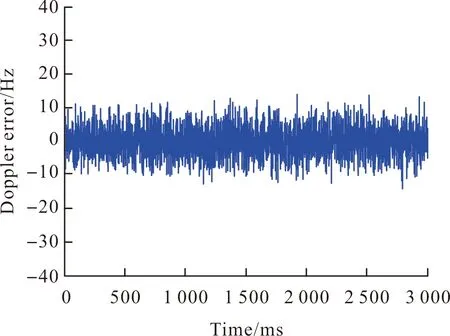
图13 INS辅助PLL2的多普勒误差Fig.13 Doppler error of INS assisted PLL2
从两图中可以看出,独立式2阶PLL测量的多普勒频率误差增大到±30 Hz的频率范围,采用INS辅助2阶PLL跟踪的多普勒频率范围有效控制在±10 Hz的范围内,使接收机载波跟踪环路的跟踪状态稳定。采用INS辅助2阶PLL载波跟踪环路可明显提高GNSS在高动态环境中的稳定跟踪能力,使GNSS跟踪环路跟踪误差明显减小,从而提高弹载GNSS导航性能。
4 结论
为提高制导火箭弹载卫星导航接收机在高动态环境中稳定跟踪能力,提出一种使用弹上INS辅助GNSS载波跟踪环路的方法,对INS辅助GNSS载波跟踪环路进行了建模和性能分析。研究结果表明:高动态环境下INS辅助2阶PLL载波跟踪环路相比独立卫星信号跟踪环路的跟踪误差有效减小,将相位跟踪误差由±0.3 rad减小至±0.1 rad,将多普勒频率跟踪误差由±30 Hz减小至±10 Hz,使得GNSS在高动态环境中跟踪能力明显提高。

