非均质推进剂燃烧演化模拟:算法与验证

张晏榕,仓 宇,杨 硕,赵 瑜,李坤霖,王利坡

(1.上海交通大学 密西根学院,上海 200240;2.上海航天化工应用研究所,上海 201109)

引 言

固体燃料燃烧问题对于基础研究和工程应用都十分重要。该问题的复杂性体现在多物理过程的耦合,包括气相燃烧、固相热传导、固相结构的表征以及气-固界面的质量能量与动量交换。

由于固体燃料使用安全、能量密度高并且成本较低而被固体火箭发动机广泛使用[1],其中氧化物颗粒高氯酸胺(AP)与聚合黏合剂端羟基聚丁二烯(HTPB)是一种常见的组合。在自维持燃烧开始后,由气相化学反应产生的热量导致固相燃料的分解,进而为气相反应提供反应物。这种双向耦合决定了界面的温度以及界面退移速率等条件。

固体燃料燃烧过程涉及多尺度,如何有效模拟不同尺度相关的子过程引起了该领域学者的广泛关注。与传统的实验试错方法相比,高质量的数值模拟对于设计及预测燃烧行为更为先进和可靠。早期研究通常是利用一维模型或一些统计平均信息。Beckstead等[2]发展了基于统计平均氧化物颗粒的AP混合物燃烧模型。而后Beckstead等[3]展示了混合推进剂火焰的总体结构,包括预混单质火焰、基本扩散火焰以及最终扩散火焰等不同部分,并指出不同火焰之间的相互作用对于理解燃烧过程的重要性,并且也讨论了压强对于火焰结构的影响。Cohen和Strand[4]结合改进的AP单质模型考虑了黏合剂部分的能量守恒关系,并对黏合剂的退移速率模型进行修正。为捕捉更多的物理细节,高维真实的仿真计算不可或缺。Miccio[5]提出一个使用五步化学反应的二维数值计算模型,其中推进剂的几何特征由表面拓扑扫描决定。Hegab等[6]基于周期性边界条件的三明治构型做了数值计算并讨论不同参数对火焰传播速度的影响。Jackson和Buckmaster[7]首次对AP和HTPB的混合燃料进行了三维模拟,实现了材料微观结构的表征以及气固两相的共轭传热等真实物理现象。此外,Jackson和Buckmaster还考虑气相与固相的强耦合以解决界面的非稳态且不均匀的退移过程[8]。Massa等采用类似的方法通过映射贴体网格到规则的笛卡尔网格来解决三维界面不规则的问题[9-10]。 Buckmaster研究非均质推进剂燃烧关于压强扰动的响应[11]。对推进剂微尺度结构的有效刻画使得结构非均质性对燃烧过程的定量影响成为可能[12]。更全面的非均质推进剂燃烧建模综述讨论可以参考文献[13]。

本研究提出一种基于重叠网格的非均质固体推进剂燃烧三维模拟框架。该计算框架避免整体求解包含气固两相的强耦合方程组,采用分离式的数值求解框架,具体而言,标准笛卡尔网格用于离散气相以保证计算稳定性,非结构化四面体网格对固相进行离散以更加精准地刻画由随机填充算法生成AP粒子结构。两套网格在计算过程中都是固定的,无需网格重建,所以有利于计算效率和数值准确性。另外水平集方法因其在处理不规则几何上的灵活性而被采用来有效地追踪气-固界面的演化退移。对于浸没在笛卡尔网格中的边界单元,可以通过施加源项以满足气相的质量、组分和能量的守恒条件。该套计算框架所有功能的集成基于开源平台OpenFOAM[1]构建。从数值上考虑,算法实现清晰便捷,对于不同边界条件都可以兼容处理,可为进一步利用数值模拟研究该类问题提供基础。

1 控制方程和气-固耦合条件

1.1 气相

三维低马赫数带化学反应的变密度流动由以下连续性方程、动量方程、组分方程以及能量方程来描述,下标“g”和“c”将分别表示气相和固相:

(1)

(2)

(3)

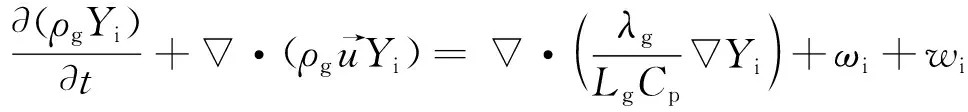
(4)

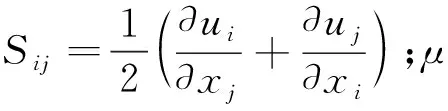
λg=1.08×10-4T+0.0133

(5)

Prandtl数和Lewis数假定为1,采用如下理想气体状态方程:

p0=ρgRT∑YiMWi

(6)

式中:背压p0设定为均一定值(由于低马赫数流动条件);理想气体常数R=8.314J/(mol·K);MWi表示i组分的摩尔质量。

1.2 固相

固相的异质形态是复合推进剂燃烧中具有挑战性的问题,退移速度和燃料的分解过程这些燃烧过程中的物理现象包括很大程度上由固体结构的异质性决定。模拟这种微尺度结构通常需要随机填充算法[14-15]。固相中的温度方程如下:

(7)

式中:密度ρc、比热容Cp和热导率λc根据该点处于AP内还是HTPB内进行取值。

1.3 气固界面的边界条件

固相气化为气相提供了质量、动量和能量的源项;与此同时,高温的气体也作用于气固界面进而影响固相内温度。这种耦合的数值精度对整个燃烧演化过程影响很大。

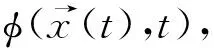
(8)

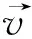
φt-rb|φ|=0

(9)

根据热裂解关系[16-17]:

(10)

式中:TAP,s、TB,s分别表示界面上AP和黏合剂HTPB的温度。在具体实施中,只有比较大的AP颗粒可以被建模求解,过小AP颗粒被均一地加入到黏合剂中。在这种情况下,根据Chen等的分析,混合材料的退移速率可以表示为[18]:

(11)

式中:α表示作为均质加入黏合剂中AP的体积分数。本研究中相关的参数见表1。

表1 计算所取参数值[8,10,16]Table 1 The parameter values used in calculation[8,10,16]

气固界面需要满足如下的温度连续热流相等的边界条件,

Tg=Tc

(12)

(13)

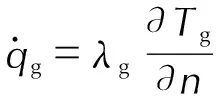
1.4 化学反应

为提高计算效率并且不影响过多的真实燃烧物理现象,本研究采用了已有文献的简化全局化学动力学[2,13],具体包含界面和气相反应的机理[9]。其中界面气化反应包括:

如果化学反应放热,此处Qs,1(2)为正值。由于实际界面反应异常复杂(物理、化学参数的确定及凝聚相影响等),该两步机理是对各种因素的总体体现。

热分解定律可以衡量气化的质量流量

(14)

式中:Ac为反应常数;ρc为固相密度;Ec为反应活化能;c为AP/HTPB;Ts为界面温度。

气相反应包括:

式中:βs为化学计量参数,类似地,βs在放热反应中为正值。相应的化学反应速率为:

(15)

式中:Di(i取1,2,3)为反应常数。这3个气相反应对应了3个不同的火焰[9]: R1对应单质推进剂火焰,R2对应基本扩散火焰,R3对应最终扩散火焰。

2 数值计算方法

在本研究中气相和固相的计算采用了两套独立重叠的网格。对于气相使用均一的笛卡尔网格,固相采用非结构的四面体网格以刻画非均质结构。采用Lubachevsky-Stillinger算法生成双球混合结构[18-19]。图1展示的填充结构是基于Miller研究中缩写为M24的SD-III-24[21]算例,红球和蓝球分别代表了直径为197.6μm和49.4μm的AP粒子,小颗粒被均匀添加到黏合剂中。

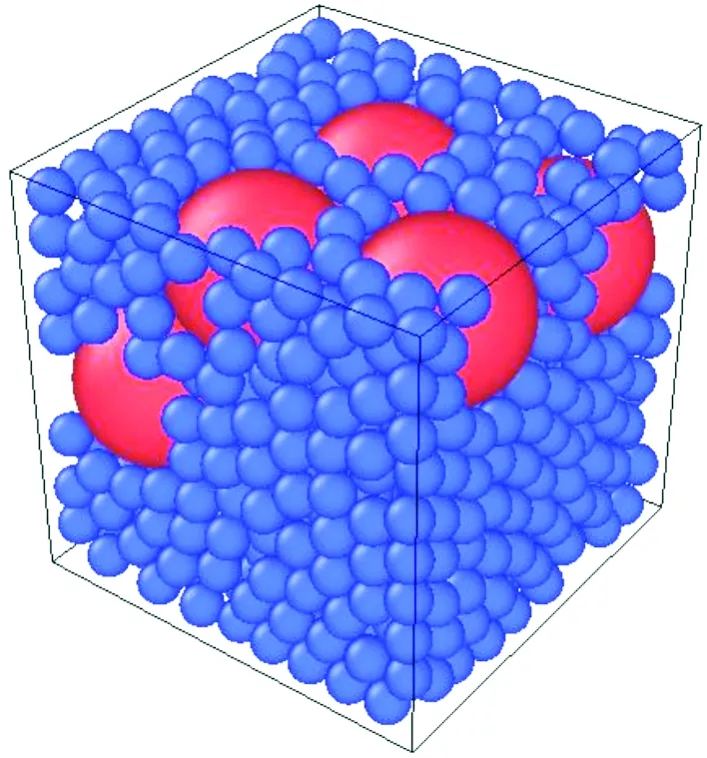
图1 M24填充模型示意图Fig.1 Schematic diagram of M24 filling model

2.1 气相和固相

气相使用投影法求解压强泊松方程,耦合处理连续性方程和动量方程[20-21]。化学反应放热带来的效果采用Pierce提出的迭代法以实现[24]。具体算法流程如下:

使用Φ=(Yi,T)表示标量,在时间步从tn推进到tn+1过程中首先进入序号为l的内循环。

第一步:在时间步tn中的每一个内循环步l使用以下初始猜测值:

(ρui)0,l=0=(ρui)n

(16)

(ρΦ)0,l=0=(ρΦ)n

(17)

ρ0=2ρn-ρn-1

(18)

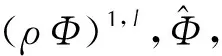
(19)

第四步:根据更新后的密度ρ1,l更新Φ,表示如下:

Φ1,l=(ρΦ)1,l/ρ1,l

(20)

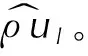
第六步:通过解泊松方程对压强进行修正:

(21)

第七步:更新速度和压强:

(22)

(23)

p1,l=p0,l+δp

(24)

重新进行第二步,重复内循环直至达到预设步数。通常在时间步从tn推进到tn+1中采用3次内循环l=0, 1, 2。这些循环完成后,对化学反应求解以更新组分和能量源项,之后时间步从tn推进到tn+1。在以上过程中,空间离散采用基于体心定义的有限体积法,对流项使用多维限制器(MLP)[23-24],方程中其他项使用中心差分。

由于气相固相网格重叠,该算法需要对浸没在固相的气相网格添加限制,具体如下:

ρg=const,ρgΦ=const

(25)

(26)

对于固相控制方程[式(7)]的空间离散选用有限体积法,时间上采用后向欧拉法。气相的时间推进使用龙格库塔法[27]。

2.2 界面条件

气固界面追踪对于固体推进剂燃烧尤为重要。图2网格展示浸没边界法[3]中的网格区分。粗线表示气固界面,在粗线以下为固相,以上为气相。如果一个网格的体心在气相/固相中,那么就定义这个网格为气相/固相网格。赋予源项的边界网格定义在气固相之间,并且体心处于气相内的网格。网格中蓝色、棕色和红色分别代表气相、固相和浸没被赋予源项的边界网格。

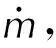
(27)

式中:ρs为固相密度;V为气相网格的体积。

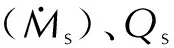
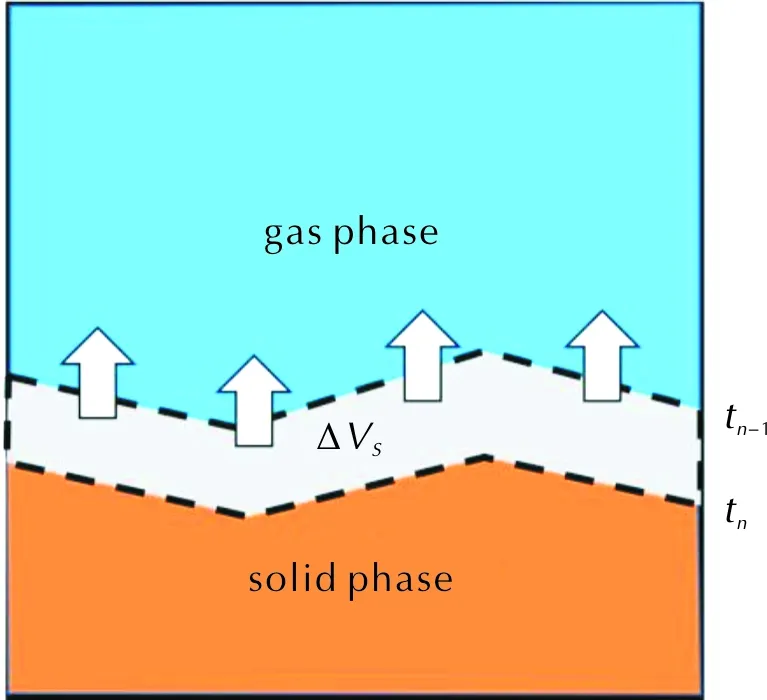
图3 一个源项网格中通过两个连续时间步水平集划分的界面计算Fig.3 Interface calculation of in one source term grid identified by two consecutive time steps level

(28)

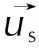
数值上,水平集界面追踪通过显示正系数法求解式(8)[28]。对于大量非结构化网格,本研究采用快速并行求解器,包括窄带快速迭代法[29]和补丁窄带法[30]以分别计算式(9)中的距离变换及界面演化。

燃烧界面上的温度十分关键,本研究通过非迭代的方式对式(13)进行离散求解[31]。在每个时间步,代表气固界面的等值面φ等于0被显式插值构建,在固相的非结构化网格中进行这种几何操作会生成三角形和四边形单元,如图4所示,每个单元会被分配到由各自临近格点组成的在气固相之间的控制体积内。基于节点的格林高斯公式由于其在高斜网格情况下具有较好的鲁棒性被用来离散温度梯度。界面温度通过对包括每个界面单元的线性稀疏矩阵进行非迭代求解获得。这套求解方式被证明拥有二阶精度[31]。

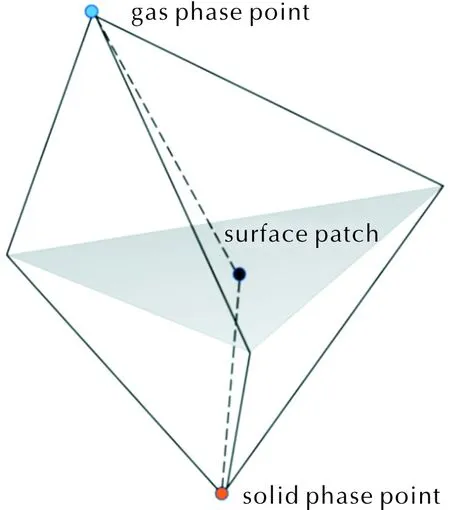
图4 为计算界面温度构建的控制体积Fig.4 Control volumes constructed for interface temperature calculation

3 结果与讨论

如图1所示,本研究选用Miller实验中基于AP的M21和M24推进剂[21]以验证本套算法。与实验的压强范围一致,选取从0.69MPa到20.7MPa的压强以研究基于仿真计算的燃速。

对于气相,计算域尺寸在x,y,z的3个方向上分别为500、500、1000μm。使用均一大小50×50×100的笛卡尔网格,每个网格的尺寸为10μm。速度边界条件在计算域底部被设置为无滑移,顶部选用零梯度,侧面选取滑移条件。压强在出口设置为定值条件。对于标量(组分和温度),所有边界条件均为零梯度。

对于固相,本研究在尺寸为500μm的计算域中生成了13.5万个非结构网格单元。温度在底部被设置为定温300K,侧面为绝热条件。顶部边界随着水平集捕捉的气固界面进行演化并由气固两相间的耦合条件确定。

如图5(a)所示压强6.89MPa条件下时间演化到0.01s的M24构型温度场。由于非均匀的局部退移速率,与真实物理过程一致,气固界面变得扭曲。在气相场中,最高温度达到约3200K。从流场中可以发现温度与速度的相互作用,图5(b)为相同设置下M24构型的温度云图及流线图。为了更清楚地展示等值面,只显示出在x方向上一半的等值面。在气固界面附近,速度方向在局部与界面垂直。界面的不规则性也导致了速度方向和大小的强烈变化。远离界面,流场受界面的影响逐渐变弱,速度方向近乎垂直向上。在界面附近主要是单质推进剂火焰,温度低于远处流场中的最终扩散火焰。

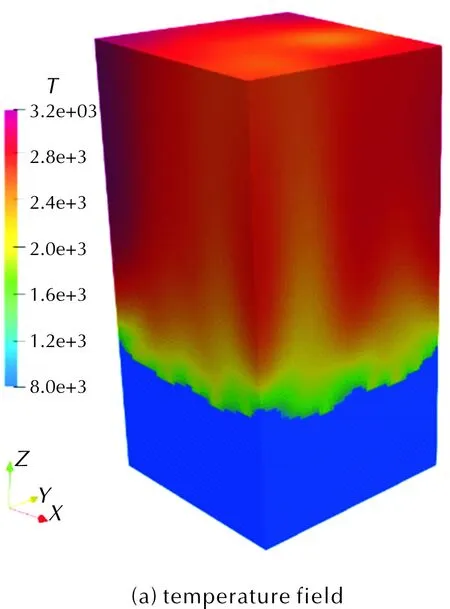
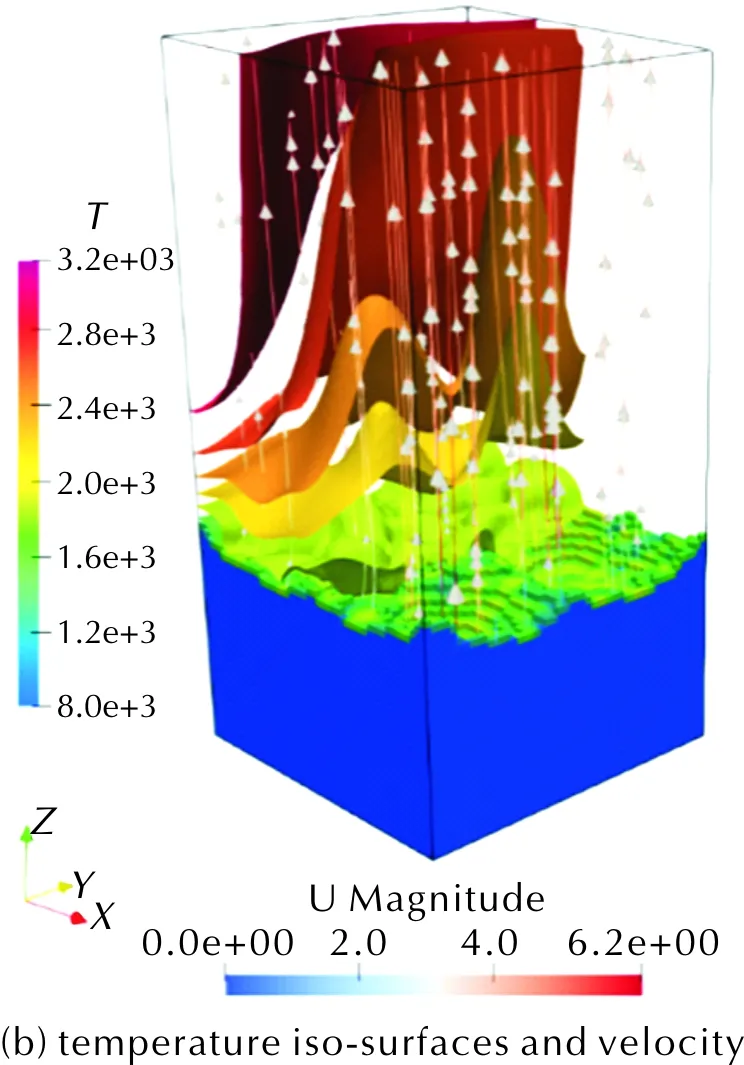
图5 6.89MPa下M24构型在0.01s时的三维示意图Fig.5 3D schematic diagram M24 configuration at 6.89MPa and 0.01s

图6和图7单独显示M24构型界面及固相区域的计算结构。其中图6为同一时刻下不同压强的情况,图7为高压下(13.8MPa)不同时刻的结果。观察发现,温度在AP与黏合剂交界附近更高。在燃烧过程中,界面会发生扭曲变形。并且热扩散层非常薄,较高的界面温度只能扩散到固相内很有限的距离中。在低压情况下(2.07MPa),界面温度较低,整体反应相对较为缓慢,界面扭曲不明显。中压情况(4.83和6.89MPa)界面扭曲较高压(13.8和20.7MPa)更为剧烈,这表明较高的压强会削弱界面上退移速度的差异,产生一个相对更平整的界面。与此同时,可以发现界面温度随压强增长而提高的趋势。

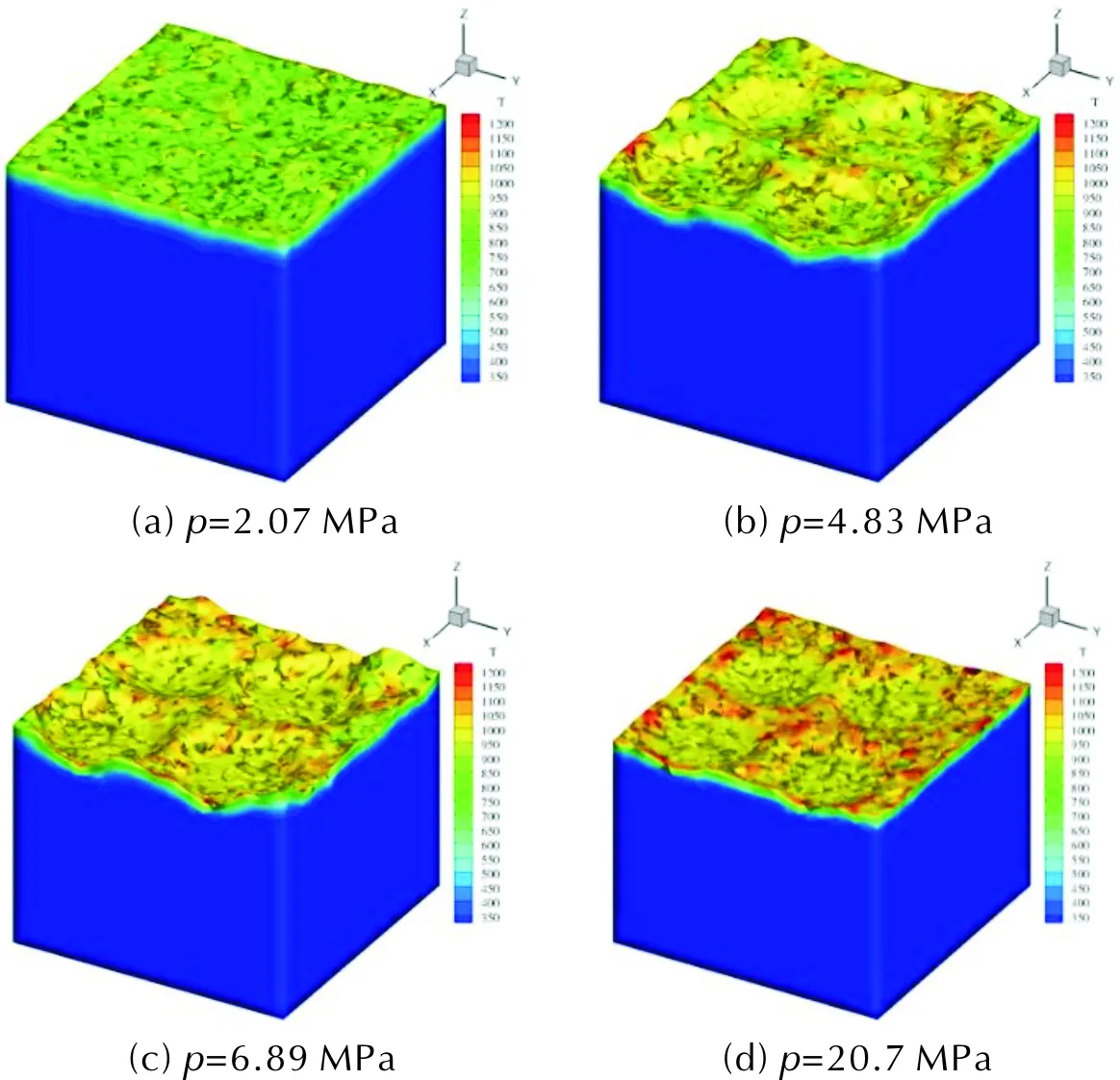
图6 不同压强下M24构型在0.004s时的燃烧界面Fig.6 Burning interface of M24 configuration under different pressures at 0.004s

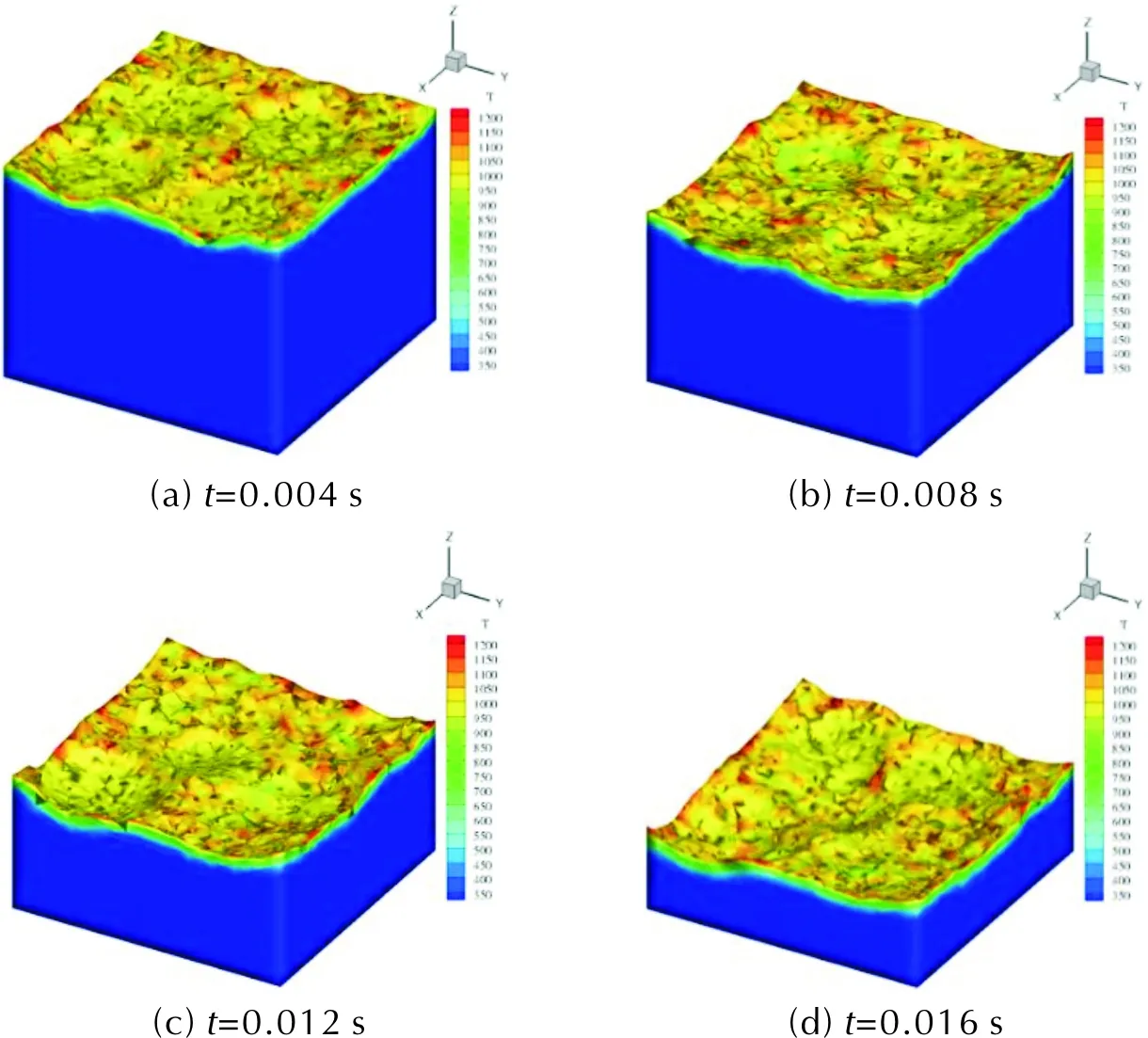
图7 13.8MPa下不同时刻M24构型的燃烧界面Fig.7 Burning interface of M24 configuration at 13.8MPa under different instants

图8为M24构型和M21构型压强从0.69MPa至20.7MPa下的计算平均退移速率与实验值及Bojko等采用Rocfire软件包计算结果的对比[21,4]。

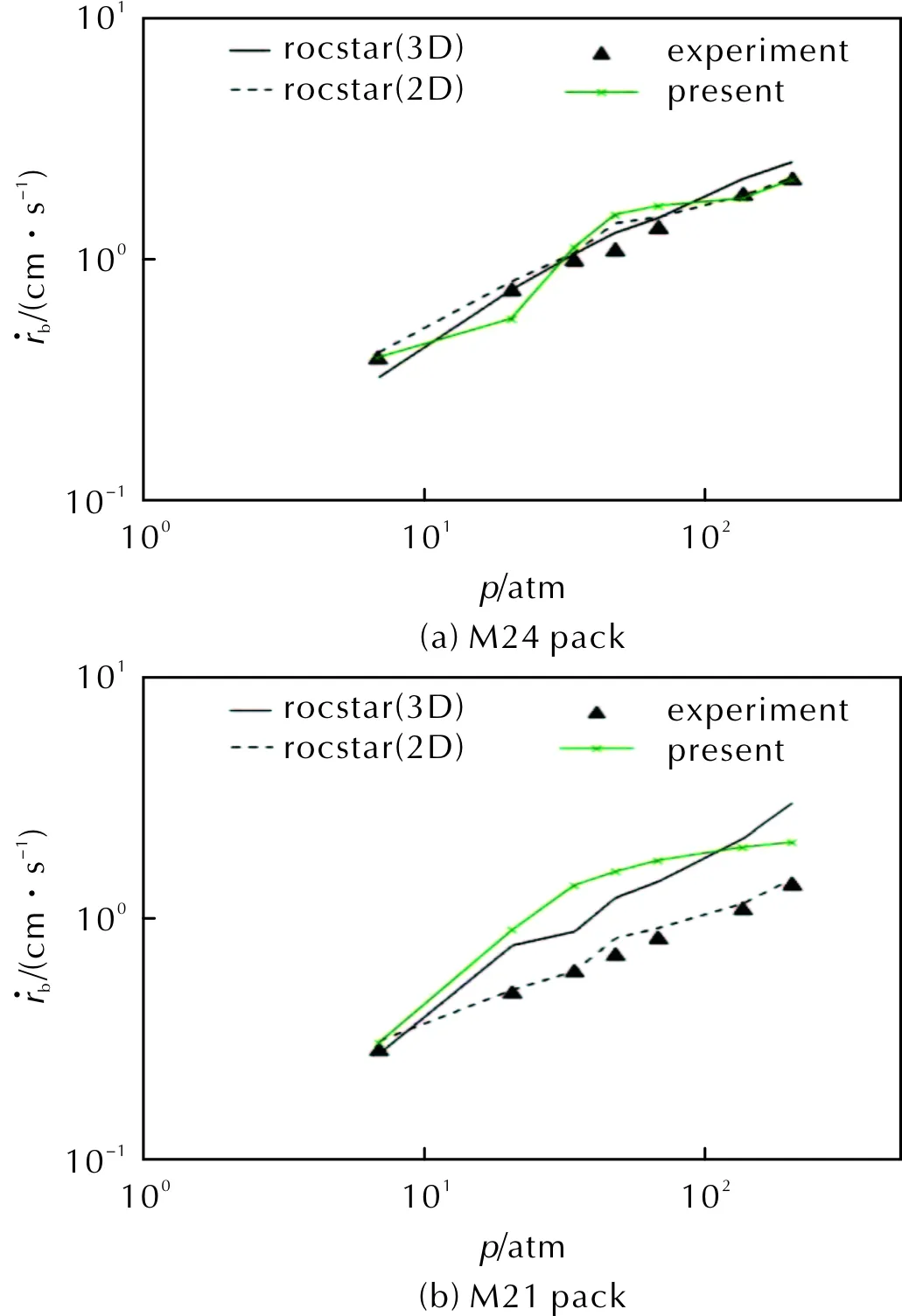
图8 M24构型和M21构型不同压强下界面平均退移速率的计算结果与对比Fig.8 Calculation and comparison of the mean regression rate of M24 configuration and M21 configuration, respectively under differen pressures

计算结果给出了合理的燃速大小并与实验趋势吻合较好。一些可能导致差异的原因包括:数值误差和模型误差,具体来说比如近界面网格分辨率可能不足以解析界面附近很小的温度流场结构,以及化学动力学的选择和固体结构刻画中的误差。

图9展示了M24构型在0.007s时分别在3.45MPa和20.7MPa的情况下,由式(15)定义的气相R1、R2及R3的化学反应速率在y方向中点切面上的云图。如之前介绍,反应R1、R2及R3分别代表了单质推进剂火焰,基本扩散火焰和最终扩散火焰。可以发现,在两种压强工况下单质推进剂火焰和初级扩散火焰都非常接近界面。在高压下,单质推进剂火焰和初级扩散火焰的化学反应速率峰值更高,说明两种火焰在高压情况都变得更为剧烈。对于最终扩散火焰可以发现其反应速率在高压下更高并且火焰整体更加接近于燃面。

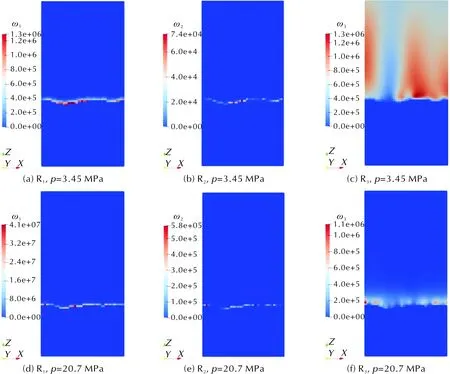
图9 M24构型在3.45MPa和20.7MPa的化学反应速率Fig.9 Chemical reaction rates of M24 configuration at 3.45MPa and 20.7MPa

需要说明的是对于当前这个典型的多尺度问题,由于火焰离界面的距离非常近(大约几微米),在高压下,该距离将会更小,因此计算的分辨率很难满足要求,单质推进剂火焰及初级扩散火焰这些尺度更小的结构可能没有很好地被解析。本研究重点强调该套新提出的计算框架的合理性及初步定性定量的验证,更高分辨率的计算和对结果的深入分析将会在进一步的研究中进行。

4 结 论

(1)本研究计算中气相计算采用均一大小的笛卡尔网格保证计算的稳定性,固相使用非结构化网格以方便刻画非均质粒子结构。两套固定网格无需随时间步重建,因此数值效率和准确性较高。

(2)非均匀退移的气固界面由水平集方法和浸没边界法追踪,质量、动量和能量的守恒关系通过对气相内的浸没边界网格施加源项以保证。

(3)针对两种构型在不同压强条件下的燃烧过程进行的讨论,该套计算框架得到的燃速与实验及已有计算结果接近,证明该数值框架的可行性与较广的适用性。