基于分子晶体序参数与K-means聚类的TNT晶型转化有限温度弦研究
常玲玲,任福德,刘英哲,葛忠学,王晓磊,邱丽莉,孟子晖,王艳红,曹端林
(1.中北大学 化学与化工学院,山西 太原 030051; 2.西安近代化学研究所,陕西 西安 710065; 3.北京理工大学 化学与化工学院,北京 100081)
引 言
转晶是物质的基本相变过程,成核是转晶的关键步骤,稀有事件方法是揭示成核本质的重要途径。目前,对于分子晶体转晶的研究[1],稀有事件方法仍具挑战性。一方面,分子晶体的分子结构复杂、不同晶型的结构相似,构建能够描述分子晶体成核的多维空间集合变量 (collective variable, CV)[2]极其困难;另一方面,利用增强采样进行最低自由能路径 (minimum free-energy path,MFEP)[3]的刻画一直是稀有事件挑战性的课题。由于分子晶体成核受尺寸效应的影响,基于平均采样的稀有事件方法致使自由能难以收敛。时至今日,稀有事件方法大多仅应用于蛋白质和核酸构象的探索[4],而对于具有明显稀有事件特征的分子晶体成核过程鲜有报道。
有限温度弦(finite temperature string, FTS) 是一种基于路径采样的稀有事件方法[5],可通过对弦路径的重新参数化,借助集合变量弦方法(string method in collective variables,SMCV)实现MFEP的快速演化。基于对分布函数参数化模型的分子晶体序参数 (order parameters, OPs) 作为CV已成功用于晶型的确定[6]。K-means聚类是一种将包含n维向量的数据集聚类迭代为k个子聚类的增强采样算法,通过对分子晶体OPs的K-means聚类,利用FTS方法有望获得MFEP快速收敛,实现分子晶体结构演化与分子运动的统一,从而在分子水平上揭示其晶型转化的本质。
TNT(2,4,6-Trinitrotoluene)是应用最广泛的熔铸炸药载体,在分子水平上对其相变过程的剖析有助于人们对熔铸过程本质的认识。本研究构建基于TNT分子晶体的对分布函数OPs,结合基于Euclidean距离和权重分布的K-means聚类方法构建平滑FTS,通过SMCV方法获得TNT分子晶体转晶的MFEP,揭示转晶机制,提出了一种在分子水平上探索炸药分子晶体转晶的有效途径,以期为高能钝感材料转晶工艺的优化提供理论依据。
1 理论与方法
1.1 序参数构建
TNT有正交(orthorhombic)和单斜(monoclinic)两种晶型,分别记为TNT(O)(CCDC:227800)和TNT(M)(CCDC:227799)[7]。TNT(O)的晶型参数为:a=14.910(2)Å,b=6.034(2)Å,c=19.680(4)Å,β=90.0°,Pca21;TNT(M)的晶型参数为:a=14.9113(1)Å,b=6.0340(1)Å,c=20.8815(3)Å,β=110.365(1)°,P21/a。
根据实验晶体结构[8]构建6×6×6 (216个分子)的TNT(O)和TNT(M)超晶胞,如图1所示,图中红色、蓝色、灰色和白色小球分别表示O、N、C和H原子。
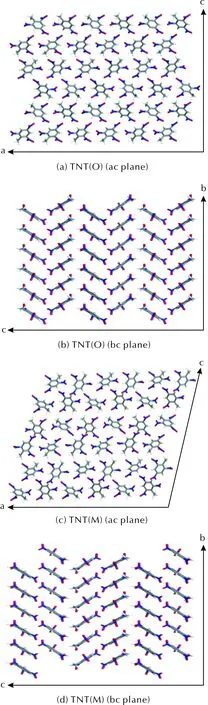
图1 6×6×6 (216个分子)的TNT(O)和TNT(M)的重要晶面Fig.1 Important lattice planes of TNT(O) and TNT(M) with the crystal size of 6×6×6 (216 molecules)
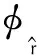
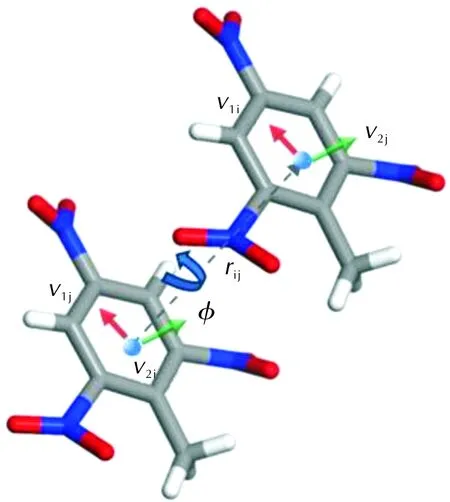
图2 基于对分布函数的序参数构建Fig.2 Construction of the order parameter based on pair distribution functions
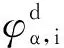
(1)
(2)
(3)
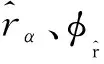
基于键序参数的键取向和相对取向分别由下式给出 (在后面讨论中,分别简称“键取向序参数”和“相对取向序参数”):
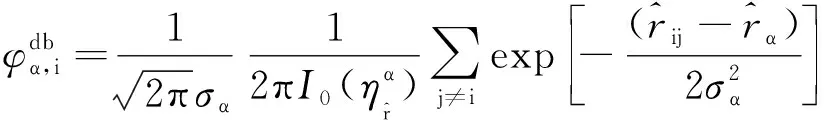
(4)

(5)
理论研究表明[11],局部序参数是描述成核反应坐标重要的集合变量。因此,在本研究中采用了两类局部序参数作为集合变量。一类是针对特定分子i的序参数,定义为体系中i的所有α-峰序参数之和,见式(6);另一类是针对体系中单元C的序参数,定义为单元C序参数的平均,见式(7):
(6)
(7)
式中:*分别表示公式(1)~(5)中的d、b、r、db和dr。
1.2 弦方法
弦方法是一种通过评估反应路径上集合变量演化的局部平均力势及其张量进行最小能量路径或MFEP的一种技术[12]。给定一组用于描述反应的N个集合变量,θ(x)=(θ1(x),…,θN(x)),x∈Rn为笛卡尔坐标,以z=z1,z2,…,zN表示的自由能定义为:

(8)
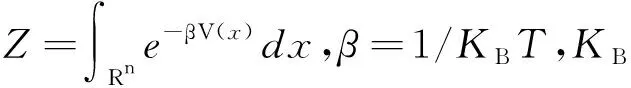
使t时刻弦z(α,t)(α∈[0,1]为弦的演化参数)[3]演化收敛到MFEP的方程为:
(9)
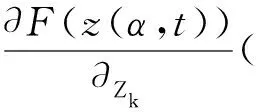
给定自由能位于za和zb的两个最小值,根据边界条件z(0,t)=za和z(1,t)=zb求解方程(9)。当t→∞,式(9)的解收敛于连接za和zb的MFEP。同时,在每个点z处的切向量平行于M(z)F(z), 即:
(10)

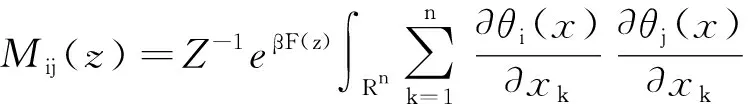
(11)

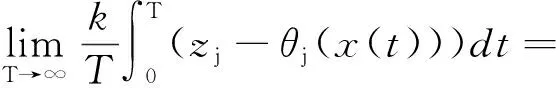
(12)
(13)
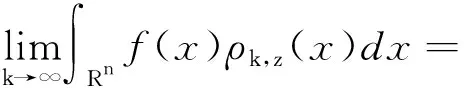
(14)
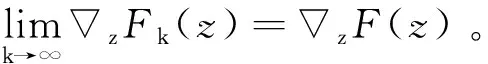
(15)
同理,根据式(11)可求得:
(16)
1.3 FTS的实现
1.3.1 初始轨迹的构建

1.3.2 K-means聚类与初始弦的平滑
众所周知,String方法在多维情况下极易陷入局部极优,这是其理论所决定的(在确定初始string的情况下,无法克服与初始string正交空间的能垒)。为尽可能防止其陷入局部极优,进行初始弦的平滑,采用K-means聚类算法进行采样,包括以下4个步骤:
步骤1:独立空间限制性采样。在每个给定代表点(副本)周围的独立空间中根据如下谐波函数采样:
(17)
(18)
式中:kd、kb、kr分别对应距离、键取向和相对取向spring系数,其值分别为20910kJ/mol、4182kJ/mol和4182kJ/mol。
通过这种方式,每个模拟都位于由每个代表点副本确定的独立空间中,在每个独立空间进行独立模拟(3×10ns)。
步骤2:K-means聚类。给出两个假设:(1)在每个独立空间中存在具有最大权重的聚类中心;(2)不同空间中最大权重聚类中心对应的序参数不同。显然,这样的假设得到的聚类中心可被视为局部重要采样点,可显示弦代表点的演化方向。
对于3×10ns的模拟轨迹进行K-means聚类。将每个独立空间的轨迹分为15个簇,借助维度加权Euclidean距离测量样本点之间的距离,在求得所有样本密度权重之后,在每个独立的采样空间中选择权重最高的点作为弦的代表点。权重ωi由下式给出:
(19)
式中:ρi、Si和ai分别表示样本点i的密度、不同数据集之间的距离以及同一聚类中不同样本点之间的距离,分别通过公式(20)~(22)计算得到:
(20)
(21)
(22)

显然,基于密度的方法在理论上更为自然,这就是本研究将样本点i的密度引入聚类算法的原因。然后,连接最大权重聚类中心形成临时弦。
步骤3:平滑函数搜索连续弦。为了获得集合坐标空间中连续弦,定义平滑函数:
(23)
通过蒙特卡洛方法计算临时弦的平滑度。首先,计算当前临时弦的平滑分数。然后,在同一空间中选择与第一个聚类中心的权重差较小的另一个聚类中心,重新计算平滑分数,根据Metropolis准则决定是否接受新的聚类中心。最后,连接新聚类中心得到平滑分数低的初始弦。
1.3.3 MFEP的刻画
(24)
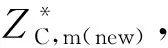
1.4 MD模拟
在300K和1标准大气压下,依据实验晶体结构,对216个分子TNT(O)和TNT(M)进行1.0ns MD模拟。借助particle mesh Ewald方法对周期性静电相互作用进行建模,引进振荡频率为25ps-1的Langevin热浴控温。平衡后,在恒定体积下退火至零温度,进行能量最小化弛豫。然后,升温至300K,在恒定体积下进行2.5ns MD模拟,时间步长0.5fs,根据轨迹借助最大似然估计方法计算式(1)~(7)的参数,确定初始序参数。
对于FTS演化的MD模拟,系综仍为NPT(300K和1标准大气压)。每一步初始构型均选择与前一步最接近新目标序参数的构型。为保持模拟的稳定性,在前一段时间内序参数约束的中心从上一步的相应值移动到新值;在后一段时间内平均每步的约束力,且初始速度均从所处温度的Maxwell-Boltzmann分布随机分配。CHARMM22力场[14]用于苯的熔化,计算结果与实验值吻合[9]。所有模拟借助自编程序和NAMD软件包[15]的CHARMM22力场进行,利用PLUMED软件包进行了序参数和自由能计算[16]。模拟流程见图3。

图3 MD模拟流程图Fig.3 MD simulation process
2 结果与讨论
2.1 TNT(M)和TNT(O)对分布函数峰值
TNT(M)和TNT(O)的对分布函数峰值在355K下获得 (实验转晶温度为351K),截至值为7.8Å。平均峰位置和集中参数见表1(括号内为355K温度下计算得到的参考结构对分布函数峰值)。与参考结构(括号内)相比,TNT(M)和TNT(O)的对分布函数峰值变化不大;对于两种晶型,对分布函数的峰值非常接近。两种晶型结构的高度相似性,不仅使构建能够精确描述其转晶的多维空间集合变量极其困难,转晶序参数发生“维数爆炸”,而且在弦的演化过程中,可能使自由能难以收敛。另外,较小的标准偏差和较大的集中参数显示了两种晶型平均质心距离、键取向角和相对取向角分布的定域性特征。
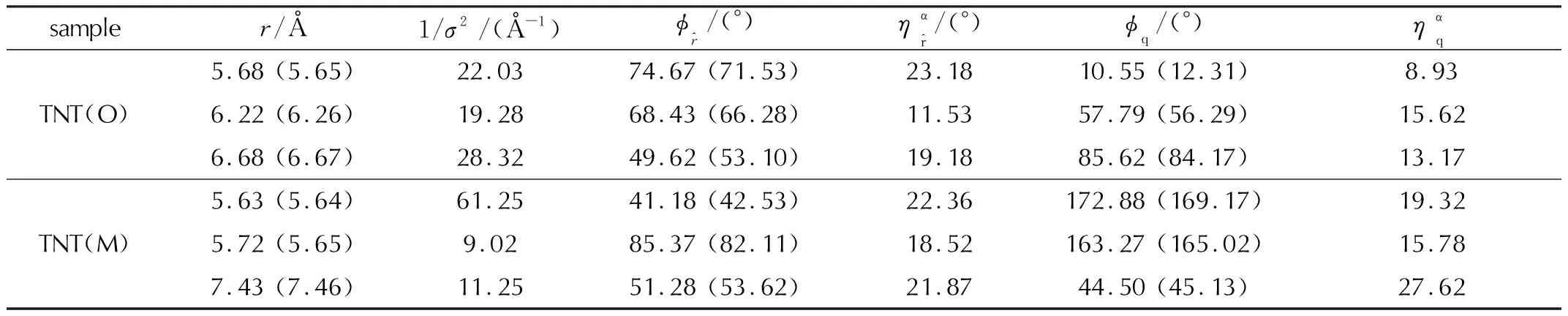
表1 355K温度下TNT(O)和TNT(M)平均峰位置及其集中参数Table 1 Average peak locations and concentration parameters for the TNT(O) and TNT(M) crystals at 355K
2.2 K-means聚类的收敛性
对于21个独立空间得到的10ns×3轨迹,分别进行了键取向和相对取向序参数的平均采样。结果发现,对于键取向序参数,ln(Convergence)值较大(-4.0~0.0),接近0.0的ln(Convergence)值可能是序参数“维数爆炸”引起的;对于相对取向序参数,迭代次数达到150次仍未见收敛,如图4所示(I、II和III分别表示经K-means聚类采样的键取向和相对取向序参数以及基于平均采样的相对取向序参数收敛),这表明基于平均的采样具有明显的分散性和不确定性。在这种情况下,来自一个采样空间中的模拟可能覆盖沿过渡路径的相邻区域,使连接相邻点的初始弦不平滑。众所周知,对于非光滑的弦,总有一些独立的采样空间不垂直于当前弦,这使得每个代表点周围的受限样本相互干扰并交织在一起,导致弦的演化方向混乱。

图4 弦演化过程中集合变量的收敛 Fig.4 Convergence of the collective variables during the string evolution
对于FTS方法,沿路径的每个代表点可被视为晶型转换过程中的中间状态。平滑的弦意味着这些中间状态可以从一端到另一端连续变化,而使弦平滑的目的是消除不相关的信息。为了得到平滑的初始弦,本文采用维度加权Euclidean距离结合密度权重的K-means聚类算法分别对键取向和相对取向序参数进行采样,发现经K-means聚类增强采样后,两种序参数的弦分别经14次和11次迭代后收敛。应用聚类算法不仅可以找到权重最大的聚类中心,解决相邻副本中高度相似序参数的区分,而且可以加快弦的收敛速度。一般地,维度加权Euclidean距离结合密度权重的K-means聚类算法具有较强的异常值干扰能力,在一定程度上,可有效避免局部最优,快速收敛到全局最优。近年来,K-means聚类算法已广泛应用于DNA、RNA和蛋白质序列的筛选和预测[17]。
2.3 最小自由能路径
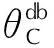
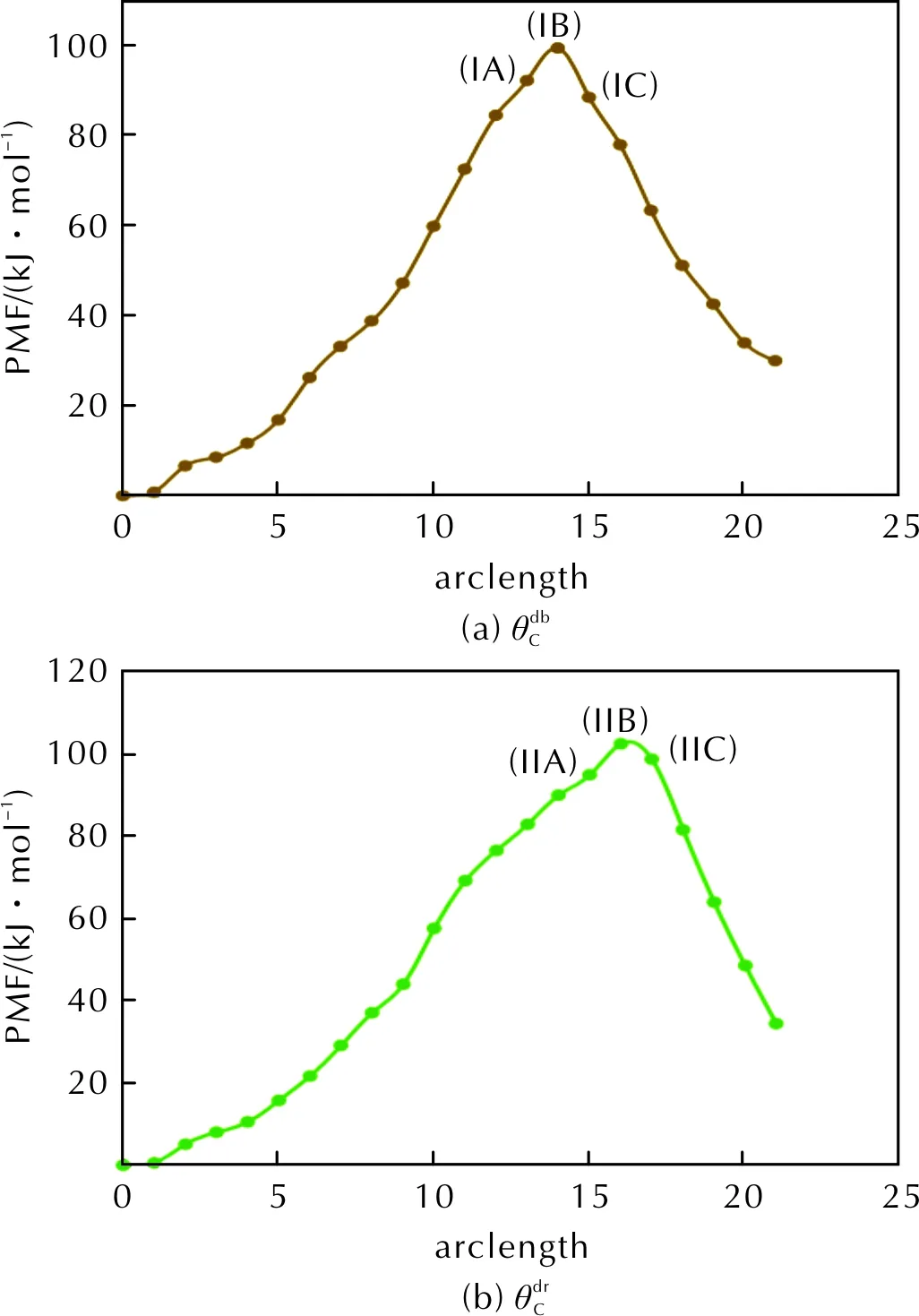
图5 PMF随弧长的变化曲线 Fig.5 Curves of PMF with arc length
由图5可知,TNT(O)与过渡态之间的PMF差值分别为102.5和99.5kJ/mol。TNT(O)与TNT(M)之间PMF的差值分别为34.3和30.1kJ/mol。由于PMF对应于27维(3×3×3)OP空间,而不是一维反应坐标,PMF比真实自由能垒高。另外,PMF值与体系的大小以及Spring系数有关。
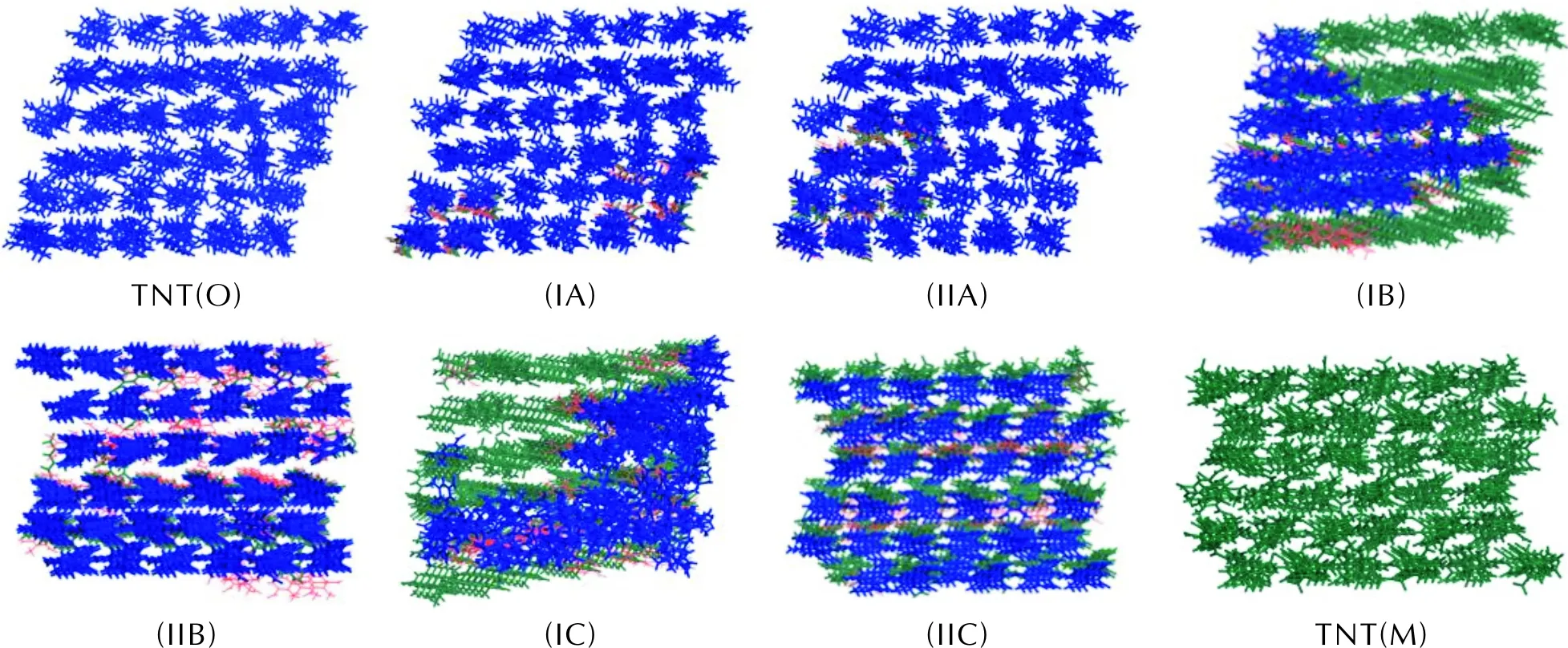
图6 FTS路径上局域序参数的变化 Fig.6 Changes in local order parameters on the FTS path
从图6可以看出,沿着TNT(O)→(IA)→(IIA)→(IB)→(IIB)→(IC)→(IIC)→TNT(M)路径,分子的类型从“完全的蓝色”逐渐变为“被蓝色包裹的零星绿色”分子簇的生成(即“界面诱导”)、“零星绿色”分子簇的增大(即“局部引发、多核非同步生成与增大”)到“蓝色被绿色吞噬”,最后形成“完全的绿色”,即“由TNT(O)向TNT(M)晶型的完全转化”。这表明,TNT(O)与TNT(M)晶型转变是界面诱导、局部引发、多核非同步发展的过程,这与Trout等对分子晶体晶型转变的研究结果吻合[19-20]。
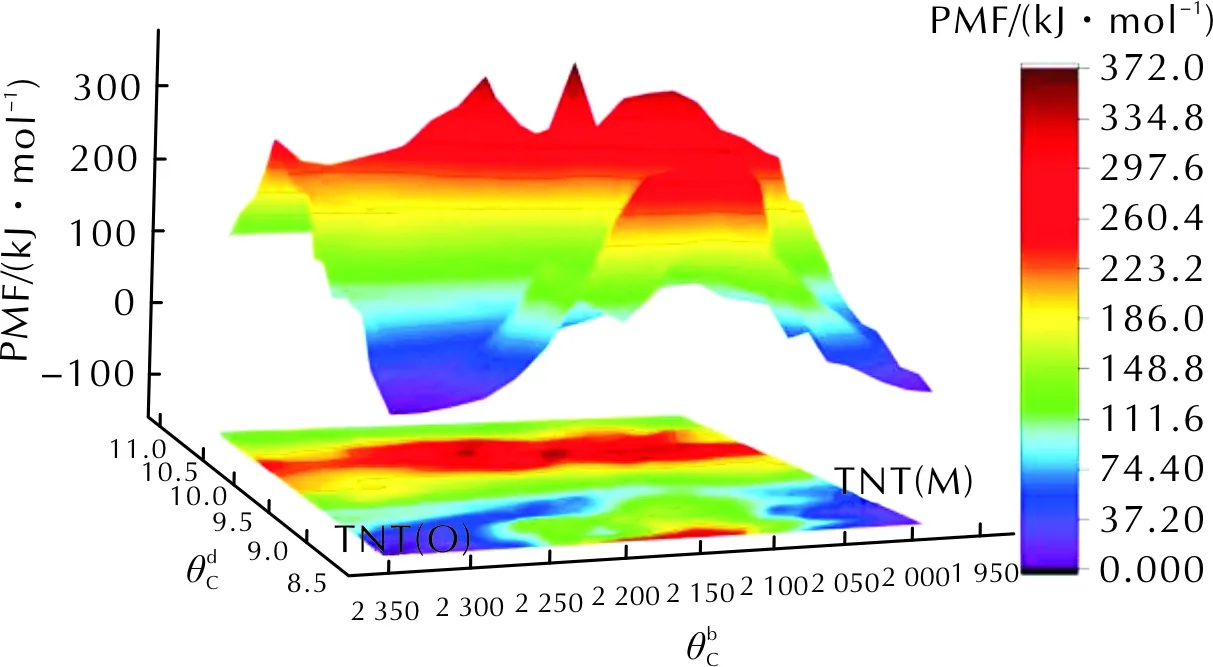
图7 沿FTS路径的PMF随全局序参数变化的3D图 Fig.7 3D diagram of PMF along FTS path with global order parameters
3 结 论
(1)基于Euclidean距离和密度权重的K-means聚类算法可以用于TNT炸药分子晶体转晶序参数的增强采样,可以改进稀有事件常规有限温度弦方法,使自由能快速收敛。
(2)基于分子晶体序参数与K-means聚类有限温度弦方法可用于TNT炸药晶型转化自由能的计算,因而可以揭示炸药分子晶体晶型转化稀有事件的本质。
(3)TNT(O)与TNT(M)晶型转变是界面诱导、局部引发、多核非同步发展的过程。

