不同海拔高度下植保无人机旋翼气动性能

王法安 ，李东昊 ，余小兰 ,3，冯 江 ，余齐航 ,5，李安楠 ，张兆国 ※

（1. 昆明理工大学现代农业工程学院,昆明 650500；2. 云南省高校中药材机械化工程研究中心,昆明 650500；3. 贵州省农业机械技术推广总站,贵阳 550003；4. 东北农业大学电气与信息学院,哈尔滨 150030；5. 上海交通大学机械与动力工程学院,上海 200241）

0 引言

当今随着农业田间管理进入数字化时代，无人机技术广泛应用于农业植保，平原地区植保无人机得到广泛的推广与应用，然而高原地区使用无人机进行植保作业仍较少，因此，植保无人机在高原地区使用得到了学者的广泛关注[1-3]。由于高海拔地区具有气压低、空气密度较低等特点，严重制约了旋翼飞行器的性能，从而使植保无人机在高原地区的实际工作性能远低于平原地区[4]。研究旋翼气动性能对于植保无人机的研究工作有重要作用，同时也能够进一步推广无人机技术在高原地区进行植保作业的应用[5-7]。因此，高海拔条件下植保无人机旋翼的气动性能研究不可或缺[8]。

国内外关于旋翼的气动性能的研究屡见不鲜。张豪等[9]借助模型建立及数值模拟方法，研究了六旋翼植保无人机下洗气流时空分布规律，揭示了植保无人机进行果树施药时冠层内部气流速度分布规律。臧英等[10]提出了一种半系留式电动多旋翼植保无人机升力测试与评价方法，实现了不同类型的电动无人机的升力特性进行综合评判。于立宝等[11-13]针对旋翼试验台开展研究，探究了不同旋翼参数下的旋翼性能和发动机性能，揭示了旋翼气动性能与发动机转速之间的相互关系。姜心淮等[14]针对同转速不同海拔高度下旋翼的悬停状态进行数值模拟，并搭建小型旋翼测量系统进行试验，论证了高原环境下旋翼表面压力的减小使拉力和功率显著下降的结论。目前，电动旋翼试验台的研制已十分成熟，开展的旋翼气动性能的测试试验也有很多成果，但高海拔环境下植保无人机旋翼的悬停性能试验较少。

为探究高海拔环境对植保无人机旋翼气动性能产生的具体影响，本研究采用叶素理论对旋翼进行分析，推导出旋翼升力、扭矩和功率的表达式；通过CFD 方法对旋翼气动性能进行数值模拟，得出悬停状态时不同海拔下旋翼流场情况和升力、扭矩及功率随转速变化情况；搭建旋翼试验台，通过控制与数据采集系统进行旋翼气动性能试验以验证仿真结果，运用数值模拟与正交试验设计相结合的方法，分析旋翼的气动性能，并取得最优参数组合，以期为后续植保无人机的研制提供理论支撑。

1 旋翼气动性能试验平台

1.1 旋翼试验台结构

为测量旋翼的气动性能，搭建旋翼试验台。选用翼形为NACA 8-H-12 的桨叶来测试不同海拔下旋翼气动性能，与超临界、超音速翼型相比NACA 系列翼型在不同倾角变化时具有较好的升阻比和俯仰力系数且适用性强，直升机、旋翼机等都适用，属当前航空领域中成熟翼型[15]。试验台总体结构由旋翼系统、传动系统、动力系统、数据采集系统、舵机控制系统及台体组成，如图1 所示。旋翼半径1.51 m，桨叶片数为2 片，叶弦平均厚度为6 mm，最大厚度9.3 mm，弦长为780 mm，叶弦扫掠面厚度20 mm。试验台结构采取“品”字型设计，符合旋翼系统在试验状态下的强度、刚度、振动以及精度等相关技术指标[16]。试验台参数如表1 所示。

表1 旋翼试验台参数Table 1 Parameters of rotor test bench

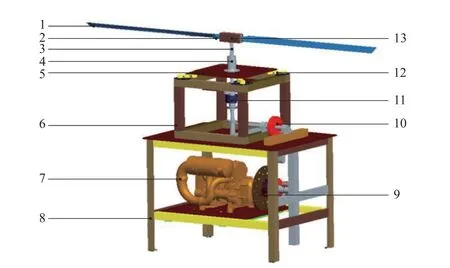
图1 旋翼试验台三维模型Fig.1 3D model of rotor test bench

机械传动系统将发动机的输出功率传递到待测旋翼，在桨叶旋转过程中产生升力，传动方式选取HTD 5M 同步齿形带传动，传动过程如图2 所示。

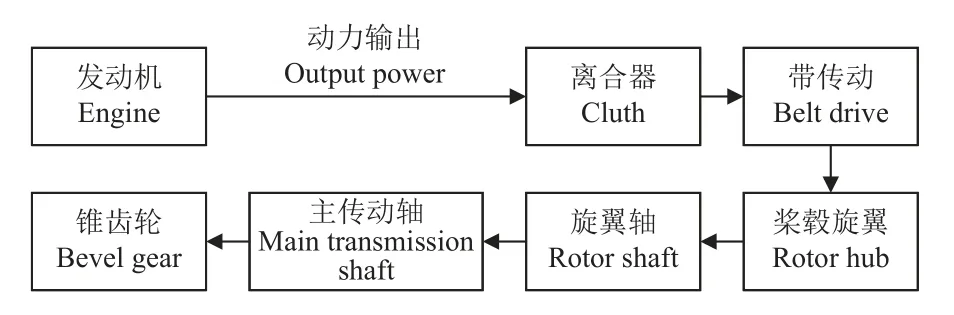
图2 传动系统流程图Fig.2 Flow chart of transmission system

1.2 旋翼试验台测控系统

1.2.1 数据采集系统

数据采集系统中单个拉压力传感器量程为40 kg，所测升力的数值为4 个传感器的测量值之和；扭矩传感器采用的型号为ZNNT-1000Nm，量程1000 N·m，该传感器属于静态扭矩传感器，能够绝对旋转；选用霍尔接近开关测量旋翼转速，型号为HL-20N1；数据采集卡型号为USB-3133A，采用LabVIEW 搭建数据采集程序。

拉压力传感器和扭矩传感器的信号送至变送器，并进行标定。在LabVIEW 软件上搭建旋翼试验台的数据采集界面。其中升力、扭矩、转速采用波形图和实时值的显示方式，用户能够直观获取数据变化的情况。旋翼试验台数据采集界面如图3a 所示，数据采集程序框图，如图3b 所示。

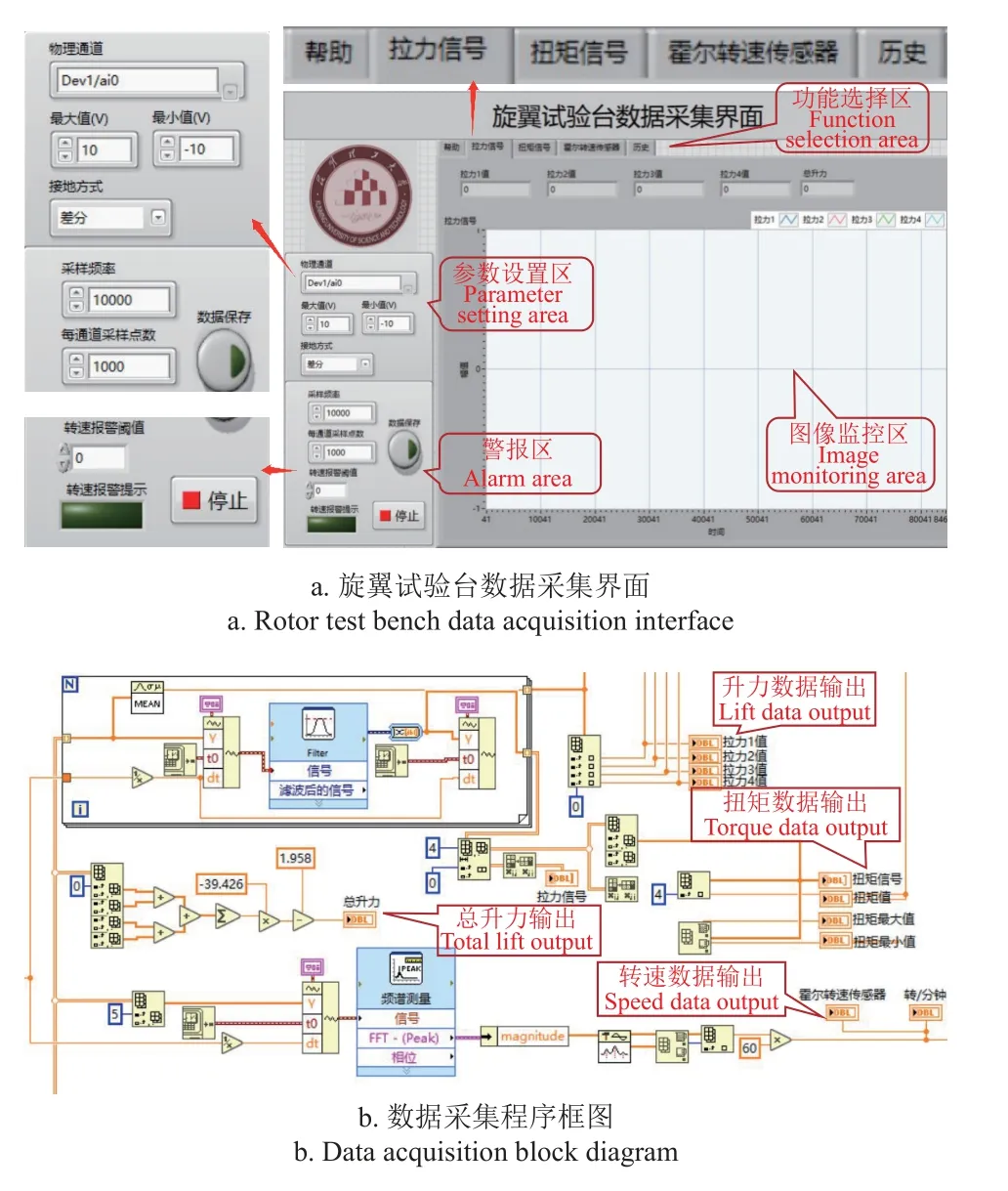
图3 数据采集系统Fig.3 Data acquisition system

1.2.2 控制系统

试验台采用的舵机型号为DS3225MG，与Arduino 控制板的数字口连接。驱动方式为脉冲宽度调制信号（PWM 信号）。发动机采用DLE430 双缸直列两冲程发动机，发动机功率30.87 kW，总质量32.25 kg，静拉力1 110 N，最高转速7 000 r/min，减速比2.55。

根据PWM 信号的占空比的大小可调整舵角[17]，标准PWM 信号周期是20 ms，脉宽范围为0.5～2.5 ms，脉宽和0 °～180 °的舵角对应。通过控制器产生脉宽不同的PWM 信号控制舵机转动。

定义Arduino 控制板的数字口作为输出接口，将舵机信号线与数字口连接。继电器输出模块中有4 个继电器模块。无线发射器和接收器型号F23-BB-TX[18]，接收发射器的指令后将信号传递给Arduino 控制板[19]。由于旋翼试验台的发动机油门调节通过拉线结构实现，因此将舵机固定在试验台上，舵机摇臂连接油门拉线，调节舵角可使油门拉线伸缩从而改变油门大小，油门增大，发动机输出转速升高，反之降低。当控制板控制舵机和继电器工作，实现发动机的无线启动、停止以及舵角的增加、减少，从而实现远程控制发动机油门大小，调节发动机转速。桨叶角需要在桨叶静止状态下松解桨叶夹具进行调节，且调整完成后要保证桨叶连接稳定，确保试验安全性，因此桨叶角只通过手动调节，电气控制不具备桨叶角调节功能。

DLE430 双缸直列两冲程发动机的电气接线如图4所示。当起动继电器接收到高电平，开关闭合，启动电机，发动机开始运行。当熄火继电器接收到高电平，开关断开，发动机停止工作。

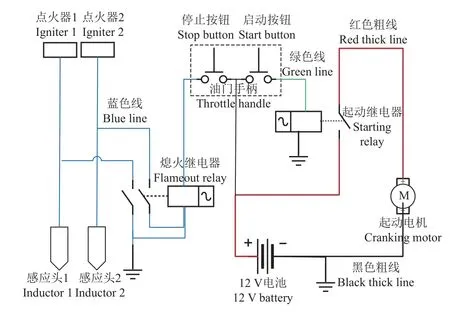
图4 发动机电气控制接线图Fig.4 Engine electrical control wiring diagram

2 数值模拟方法

2.1 网格划分及数值模拟

旋翼桨叶围绕旋翼轴的转动产生旋翼流场，其中桨叶的运动状态是旋翼流场的主要影响因素[20]。为探究旋翼桨叶的气动特性和数值模拟求解，采取叶素动量理论研究桨叶的气动特性。

叶素是指桨叶径向方向的微小段，如图5a 所示，无数个叶素构成桨叶，叶素理论为分析小叶素的运动状态与受力影响。因此，为了构建叶素的几何特性与旋翼运动状态间耦合关系模型，利用叶素径向空气动力积分叠加获取桨叶的升力和功率与旋翼几何特性的关系[21]。叶素在桨叶中的对应表示法如图5b 所示。在垂直飞行时，悬停状态下桨叶桨距是固定不变的，此时桨叶上最大的力为向外侧的离心力，将叶素沿着桨叶展向积分即可获得离心力。

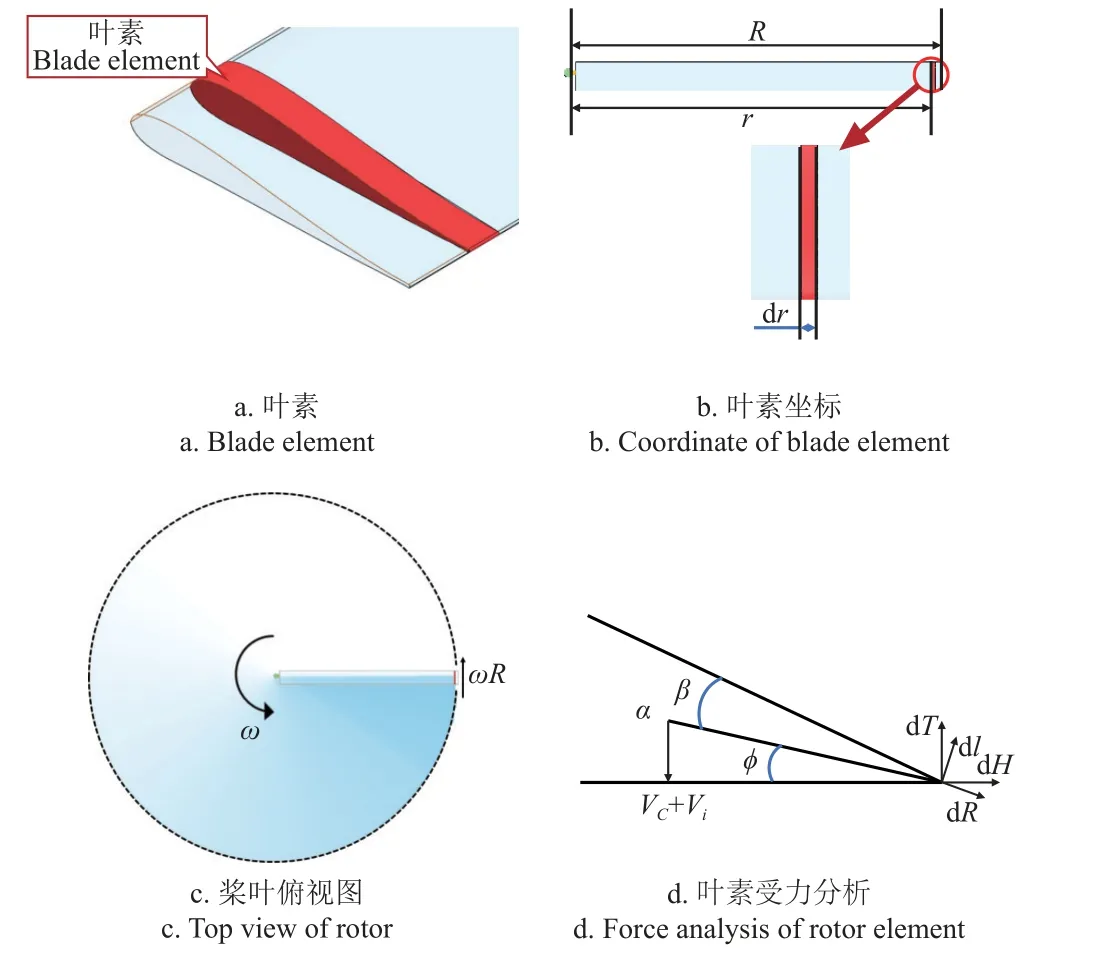
图5 旋翼及其受力分析图Fig.5 Rotor and its force analysis

桨叶沿旋翼轴以ω 的角速度逆时针方向旋转，其转动俯视图如图5c 所示，桨叶半径R，可得桨尖处的速度为ωR，桨叶速度记作v。此时俯视图中的叶素受力情况如图5d 所示。

叶素理论的桨叶面积s=ncR，其中n为桨叶片数；c为桨叶弦长，m。结合相关参数进行数值模拟仿真可得升力T、扭矩M、功率P的确定解析解[22]。

式中CT、CM、CP分别为升力系数、扭矩系数、功率系数；ρ为空气密度，kg/m3；v为桨叶线速度，m/s；s为桨叶面积，m2。

运用CFD 方法进行旋翼悬停状态分析，首先采用ANSYS ICEM 进行结构网格划分。构建旋翼试验台动域和静域模型。其中包裹桨叶的动域半径2.18 m，高0.31 m。为保证计算结果的精确性，降低因计算域过小而导致模拟失真，假设外部静止域足够大，该区域底面半径为3.5 m，为了避免产生回流，桨叶中心到静域上底面与下底面分别为1 和10 m。

对动域和静域进行三角形面网格划分，如图6a、6b所示，为提高模拟精度，细化旋翼节点进行网格优化，使网格整体质量雅可比比率都大于0.3，采用自上而下的方式生成四面体网格，旋翼体网格数量共计58 万。由于模拟重点在于旋翼，同时为了节省计算资源，静域的网格尺寸设置为400 mm，静域体网格共420 万。

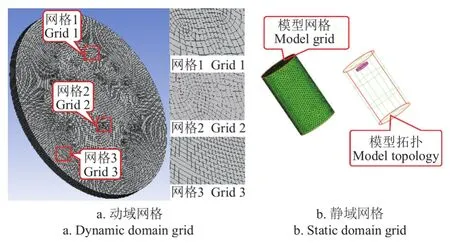
图6 网格划分Fig.6 Grid meshing

使用Fluent 软件对旋翼模型进行数值模拟，需分别设置边界条件、湍流模型及求解方法。将动域上、下底面分别设置压力出、入口边界条件，旋翼设为壁面边界条件，壁面无滑移，动域和静域均设置成流体。湍流模型控制方程采用剪切压力传输SST(shear stress transfer)kω 模型[23-24]。使用基于压力的双精度稳态求解器，计算方法为SIMPLE(semi-implicit method for pressure linked equations)算法，转动方式采用多参考坐标系MRF(markovrandom field)模型。为增强计算的精度，数值模拟中对流项、比耗散率的空间离散、湍流动能都设置为二阶迎风，将松合因子设置为0.6，后期可根据收敛情况进行调整，计算步长 3000 步[25]。残差曲线默认的设置为10-3，将各项残差值设置为10-5，在计算过程中残差曲线会将每步计算的各项值的残差以曲线形式呈现，直到各项的残差值低于所设定的值，计算收敛。

2.2 数值模拟大气环境参数设定

标准大气压下，海平面的大气开氏温度T0为288.15 K，摄氏温度为15℃，压强P0为101.325 kPa；密度为1.225 kg/m3；在11 km 以下的对流层中，海拔高度每增加1 km，温度降低6.5℃[26]。高度h处的气温Th为

式中h为海拔高度，m；Th为高度h处的大气温度，。

海拔4 km 范围内，重力加速度变化较小，故不考虑重力加速度随高度的变化情况，则高度h处的大气压强Ph为

空气密度由温度和压力决定，随海拔高度的增加而降低，其计算式为

式中 ρ为高度h的大气密度，kg/m3。

由上述分析可知，海拔高度影响大气温度、压强以及密度，为研究海拔高度对旋翼性能的影响，计算得到海平面到4 km 海拔高度的大气温度、压强以及密度，如表2 所示。本研究无人机的应用背景是农业领域，而世界最高农耕的海拔上限为4 750 m，过高的海拔并无实际意义，所以本文研究选取海拔高度至4 km[27]。

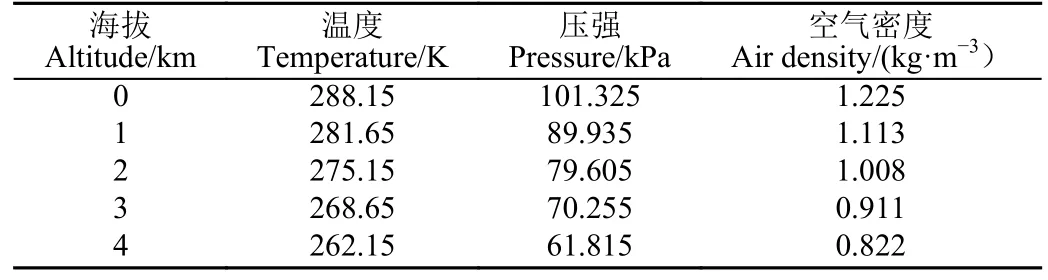
表2 不同海拔高度下的大气参数Table 2 Atmospheric parameters at different altitudes

2.3 数值模拟结果与分析

在数值模拟仿真中设置不同大气参数（大气温度、大气压强、大气密度）模拟不同海拔高度，用监视器监测不同海拔条件下的升力曲线图。待各项值收敛且计算完成后对数值模拟结果进行初步的后处理分析，在海拔高度为0，转速为1 000 r/min 时，旋翼升力变化曲线示例如图7。

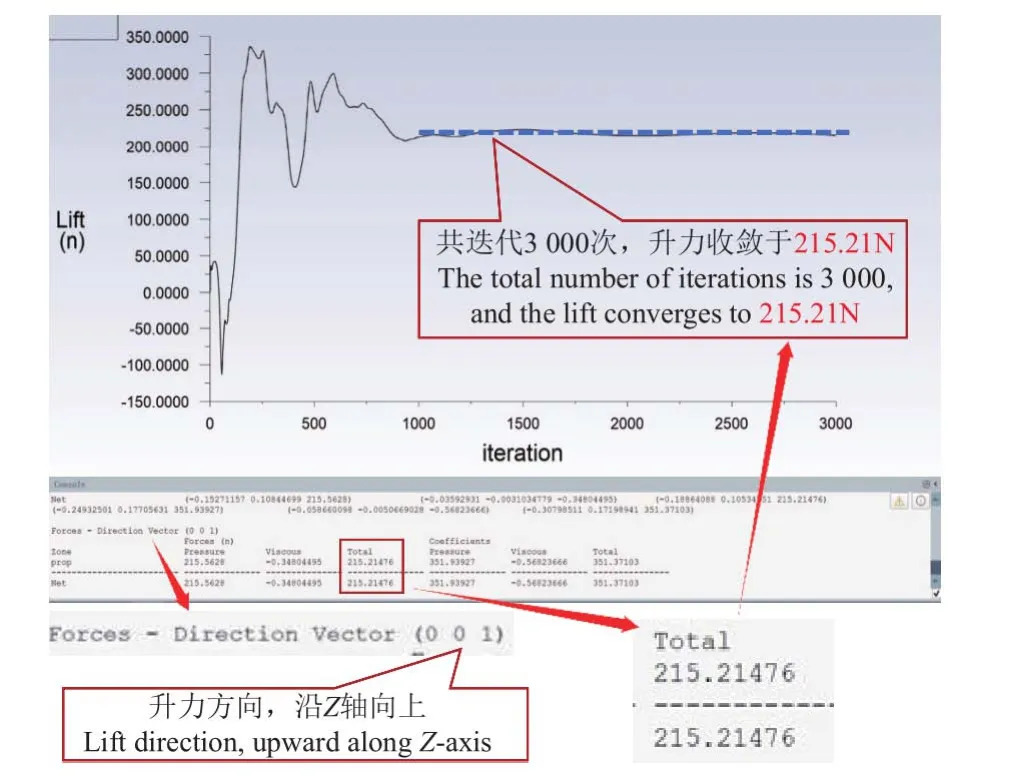
图7 升力变化图Fig.7 Tension variation diagram

由数值模拟结果得到旋翼升力随海拔高度的变化曲线如图8a 所示。旋翼升力的数值模拟结果表明：在海平面到海拔4 km 范围内，随着海拔高度的增加，旋翼升力有明显下降；同一海拔高度下，升力与转速成正比。转速1 000 r/min 时，与海平面相比，海拔2 km 处升力降低约21.6%；转速1 200 r/min 时，与海拔高度0 相比，海拔高度2 km 处升力降低约20.22%。

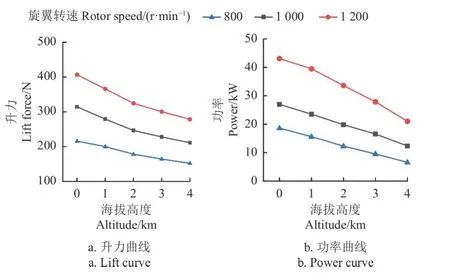
图8 不同海拔高度下旋翼性能Fig.8 Rotor performance at different altitudes

用监视器监测不同海拔条件下的扭矩曲线，并将数值模拟的扭矩换算为功率，得到功率随不同海拔高度的变化曲线，如图8b 所示。数值模拟结果表明：在海平面到4 km 范围内，随着海拔高度的增加，旋翼功率明显下降，下降速率也增大；相同海拔高度下功率随旋翼转速的增加而增加。转速为1 000 r/min 时，与海拔高度0 km处相比，海拔2 km 高度处的旋翼功率降低约26%。

3 性能试验与分析

3.1 试验准备

为了验证本研究所采用数值模拟方法的有效性，搭建旋翼试验台进行实地试验，场地选在昆明理工大学现代农业工程学院附近空地，试验时，实际海拔高度1.941 km，大气温度14 ℃，大气压力80.1 kPa，大气湿度20%。试验环境中存在常见自然风，实际风速小于1.5 m/s，试验中旋翼转速远大于环境风速，环境风对旋翼气动性能影响极小，在数值模拟中，有横向环境风对比无环境风在对应旋翼转速下产生升力无较大变化，因此，可忽略环境风对试验的微弱干扰。

将试验台放置地面后利用水平仪将底部调至同一水平面。旋翼试验台如图9 所示。

图9 旋翼试验台实物图Fig.9 Physical picture of rotor test bench

3.2 试验结果与分析

3.2.1 验证试验

在海拔高度1.941 km 的大气环境下分别进行旋翼转速为800、1 000、1 200 r/min 的3 组试验，试验设定转速与数值模拟仿真中的旋翼转速对应。通过试验得出在不同旋翼转速下的升力与数值模拟结果比较，如图10 所示。

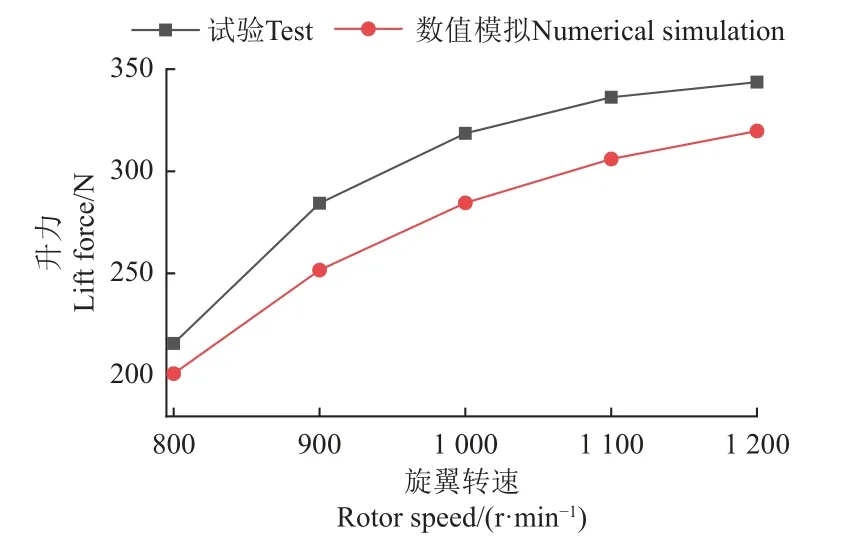
图10 数值模拟与试验结果Fig.10 Numerical simulation and test results

通过对比试验得出的升力高于数值模拟结果，试验结果与数值模拟结果的变化趋势一致，升力的误差在20～30 N 范围内，相对误差在11.5%以内。造成误差的原因主要是发动机在高速状态下加、减速，冲击负荷过大，超出同步带承受范围，出现短暂的传动失效现象，若此时霍尔传感器检测到目标转速，停止加速，则传动系统正常运转，传动不再失效，不稳定阶段的转速、升力等数据受摩擦影响较大，但稳定后的转速即采集的数据略高于目标转速，经过测试，发动机转速在1 200 r/min 范围内，发动机与同步带之间发生失效会产生120 r/min 以内的转速损失。考虑实际试验环境与预期参数设定有一定的差距，如环境风速，虽然影响较小，但仍会产生影响，结合本研究，升力误差在20～30 N 范围内，与转速损失的结果有对应关系，验证了数值模拟结果。同时，数值模拟采用二阶迎风格式，精度虽比一阶迎风格式高[28]，但仍存在假扩散问题，导致数值计算结果出现误差。总误差率小于10%，试验结果与数值模拟结果误差的幅值或比率均在合理范围内，本研究所采用的数值模拟方法有效。

3.2.2 二次旋转正交组合试验

由于旋翼上表面和下表面的形状不同，旋翼转动时气流经过上下表面的流速存在差异，由伯努利原理可知，上下表面的压力差的出现是产生升力的原因；本研究中旋翼翼型固定，则气流流场是影响升力的关键因素，而旋翼转速和桨叶角是直接影响流场的因素，因此选取桨叶角和旋翼转速作为试验因素。

为探究不同海拔高度下，桨叶角和旋翼转速对旋翼性能以及旋翼试验台性能的影响，采用二次旋转正交组合试验方法在海拔1.941 km 环境下开展试验，与本团队在海拔134 m 的试验结果对比[13]，两海拔高度处的试验方案相同，旋翼性能试验中试验因素为桨叶角x1、旋翼转速x2，试验指标为升力；旋翼试验台性能试验指标为扭矩、功率。试验因素水平编码如表3 所示。试验方案和结果如表4 所示。

表3 因素水平编码表Table 3 Factor level coding table

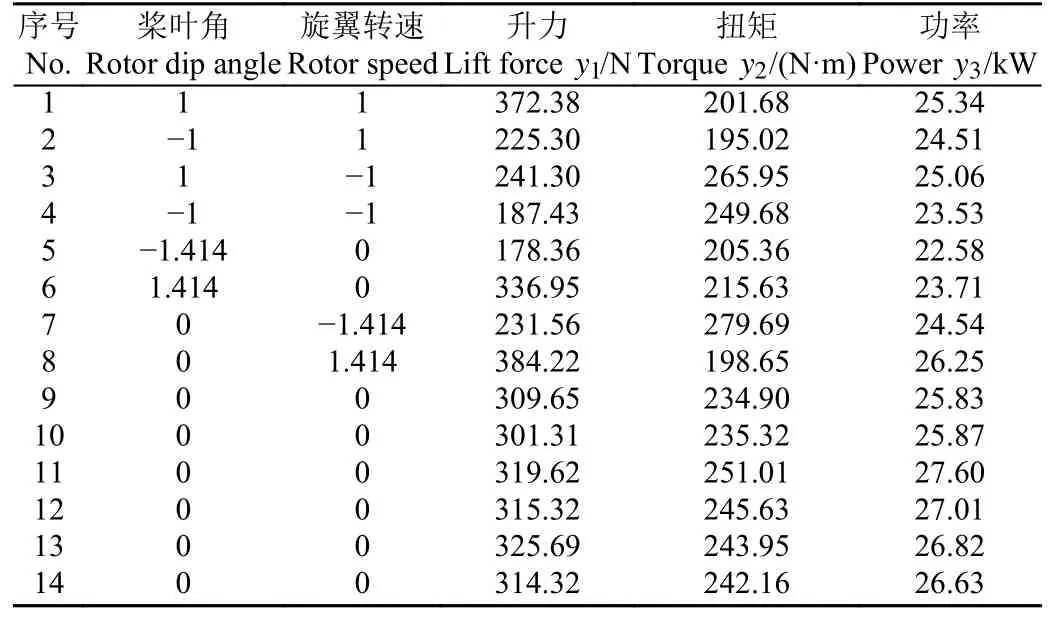
表4 试验方案和结果Table 4 Test scheme and results

通过方差分析和建立回归模型得出各因素对升力的影响。方差分析如表5 所示，表中调整R2为0.934 5，表明回归模型与试验值符合程度较好。模型F值为35.25，P＜0.01，表明升力与桨叶角和旋翼转速有较显著的相关关系，拟合水平较好。

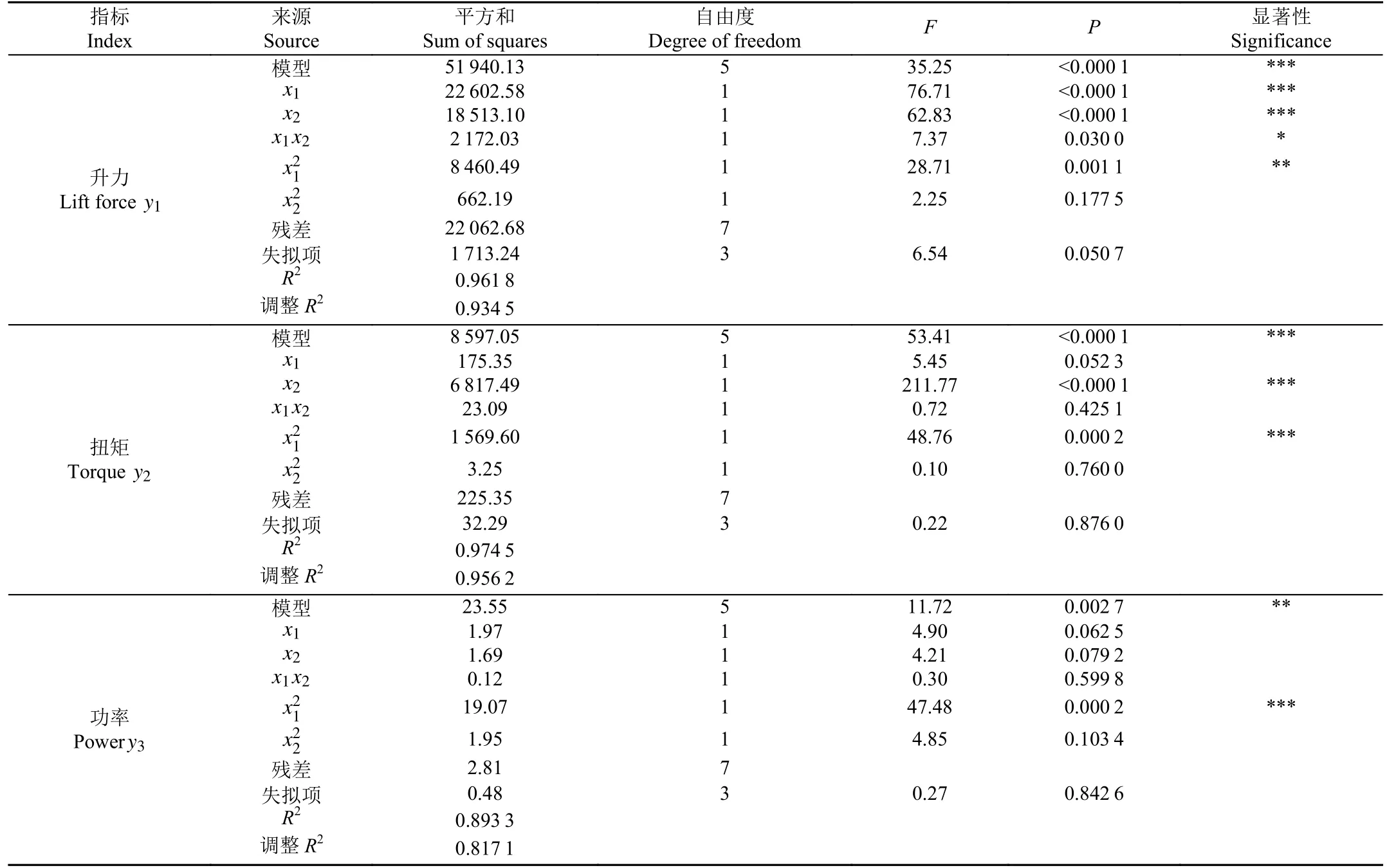
表5 回归模型方差分析Table 5 Regression model variance analysis

去掉不显著因素后建立关于升力、扭矩、功率的二次回归方程如下：

桨叶角和旋翼转速交互作用的响应面如图11a 所示，由图11a 可知，桨叶角为9 °～13 °，旋翼转速在1 080～1 200 r/min 时，旋翼升力较高。在旋翼转速一定时，随着桨叶角的增大，升力先上升后下降；当旋翼转速变化时，升力变化范围较大。优化结果为旋翼转速1 116 r/min，桨叶角10.44 °时升力为356.28 N。

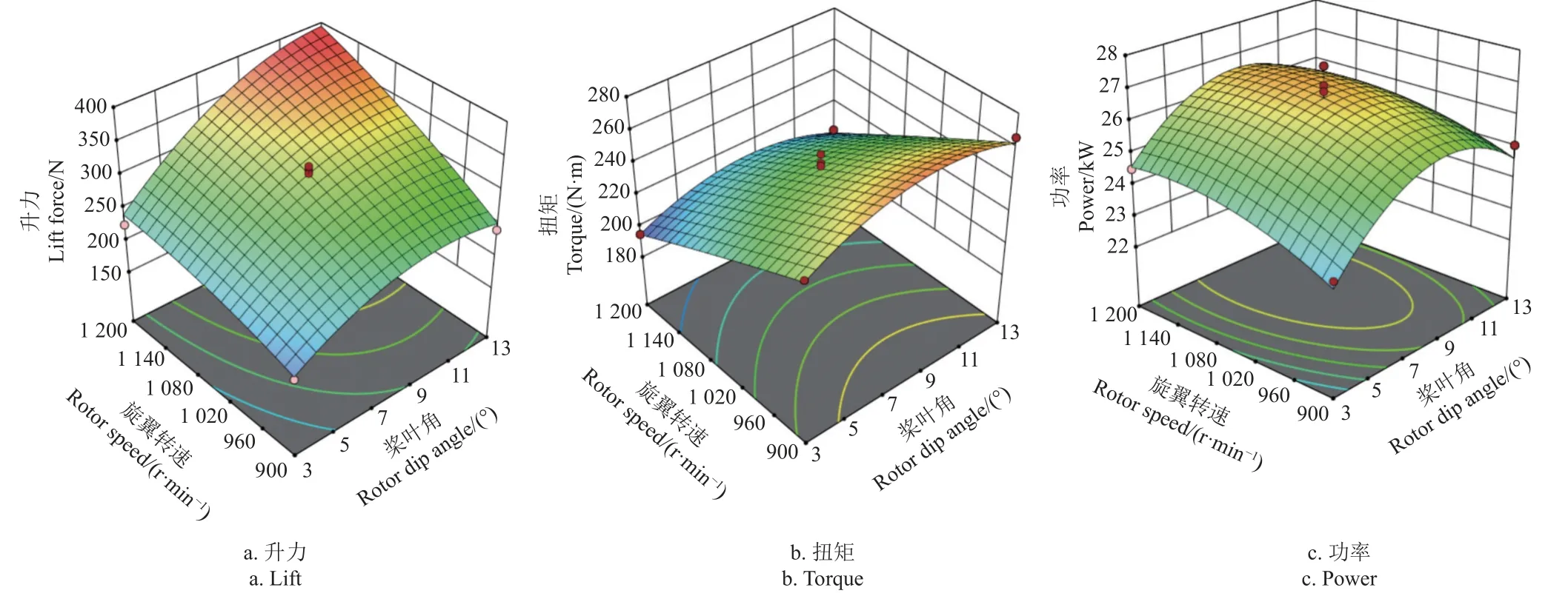
图11 响应面分析Fig.11 Response surface analysis

扭矩的响应面如图11b 所示，由图11b 可知，在桨叶角为11 °～13 °，旋翼转速在900～960 r/min 时，旋翼轴扭矩较高。在旋翼转速一定时，随着桨叶角的增大，扭矩先上升后下降；在桨叶角一定时，扭矩与旋翼转速成反比；当桨叶角变化时，扭矩变化范围较大。对响应面模型进行分析求解，优化出最佳组合，即旋翼转速在1 079 r/min，桨叶角在11.418 °时，扭矩为232.25 N·m。

由功率响应面如图11c，桨叶角为7 °～11 °，旋翼转速在1 020～1 080 r/min 时，旋翼功率较高。当旋翼转速一定时，随着桨叶角的增大，功率先上升后下降；桨叶角一定时，功率随转速的增大先上升后下降；当桨叶角变化时，功率变化范围较大。对响应面模型进行分析求解，优化出最佳组合，即旋翼转速在1 091 r/min，桨叶角在10.192 °时功率为26.59 kW。

根据上述试验结果可知旋翼转速在1 116 r/min，桨叶角在10.44 °时升力取得最大值为356.28 N，此时扭矩为227.35 N·m，功率为26.54 kW，根据发动机功率30.89 kW 可得旋翼试验台效率为85.92%。

本团队2019 年1 月19 日在东北农业大学（海拔134 m）开展试验，获得的最优方案为桨叶角12.39 °、旋翼转速1 200 r/min，此时旋翼升力为459 N、驱动力矩300 N·m，发动机功率为27.6 kW，旋翼试验台效率为89.35%[13]。

对比上述结果可知：在海拔1.941 km 处实地试验结果与海拔134 m 处的试验结果相比，旋翼升力下降约22.38%，旋翼驱动扭矩下降约24.21%，此时发动机功率下降约3.99%。这是由于两个试验场地之间海拔不同导致大气密度、压强等参数有差异。数值模拟结果得出旋翼转速为1 200 r/min时，海拔2 km 处的旋翼升力比0 km下降20.22%，与实地试验数据相吻合，由此可见数值模拟结果和试验结果相差较小。导致误差的因素有传动系统同步带失效、采集系统中传感器的数据误差。由于试验只涉及海拔、环境参数间的差异，在其他试验条件相同的情况下，试验中的误差因素不影响最终结论。

4 结论

本研究针对现有试验台的不足，在数值模拟的基础上完成了旋翼试验台的搭建，开展了旋翼性能的仿真分析和试验并与前期试验结果进行对比分析，主要结论如下：

1）对翼型为NACA 8-H-12 的旋翼进行建模，采用CFD 方法对旋翼的气动性能进行数值模拟，数值模拟结果表明：随着海拔高度的增加，升力及功率减小；同一海拔下，升力和功率随转速的增加而增加。

2）搭建旋翼试验台，采用正交试验设计方法进行试验，旋翼转速在1 116 r/min，桨叶角在10.44 °时升力取得最大值356.28 N，此时扭矩为227.35 N·m，功率为26.54 kW，旋翼试验台效率为85.92%。

3）该试验台在海拔1.941 km 处的试验结果与海拔134 m 处试验结果对比可知，旋翼升力下降约22.38%，旋翼驱动扭矩下降约24.21%，发动机功率下降约3.99%。