两层优化辅助的大规模高维多目标优化算法

时振涛,常晨芳,李晓波,王 浩

(1.太原科技大学计算机科学与技术学院,太原 030024;2.太原科技大学电子信息工程学院,太原 030024)

多目标优化问题[1]在工程和科学领域中广泛存在,例如:车辆调度问题[2],森林规划问题[3]等。其数学表达式如公式(1)所示:

(1)

其中,M为目标函数的个数,Ωn为n维决策空间且X⊆Ωn,x=(x1,x2,…,xn)为n维决策向量,f1(x),f2(x),…fM(x)构成目标空间。在多目标优化问题中,由于多个优化目标彼此冲突,即某目标性能的提高可能引起其他目标性能的降低,所以在求解多目标优化问题中往往需要获得的是一组解,称为帕累托最优解[4,5](Pareto set,简称PS),该组解相应的在目标空间的解集称为帕累托最优面(Pareto optimal front,简称PF).由于进化算法单次运行可以得到一组解,所以其被广泛用于解决多目标优化问题,称为进化多目标优化(Evolutionary multi-objective optimization,简称EMO).

到目前为止,进化多目标优化算法根据使用的环境选择的策略不同可以分为四类:第一类是基于支配关系的方法,如NSGAII[6];第二类是基于分解的方法,如MOEAD[7],RVEA[8],MaOEA-ARV[9]等;第三类是基于指标的方法,如IBEA[10],HyPE[11],MaOE-CSS[12],NSPI-EMO[13],还有其它方法,如采用支配和分解相结合的方法MOEADD[14]和NSGA-III[15].目前求解大规模高维多目标优化算法大致分为三类:第一类是基于决策变量分析。在MOEA/DVA[16]中,Ma和liu 等人将决策变量分成多样性相关和收敛性相关两类,然后采用不同的优化方法对两类子问题分别优化;同样,Zhang等人在LMEA[17]中提出采用聚类的方法将决策变量分为两类,然后分别采用收敛性和多样性两种不同的策略对收敛性相关变量和多样性相关变量进行优化。但是基于决策变量分析的方法的缺点在于当决策变量维度增大的时候,计算量会增大。第二类是基于分解的策略并利用协同进化框架(Cooperative Co-evolution,简称 CC)来提高种群的搜索效率。在CCGDE3[18]中,Antonio和Coello将决策空间分组,对每个子问题分别进行优化。在该类方法中,分组的策略对优化的结果有很大的影响,常见的分组方式有:随机分组、线性分组、有序分组和差分分组。但是它的缺点在于在不知道决策变量的相互作用和组的大小的时候,CC的算法效果依赖于选择什么样的分组策略。第三类是基于问题转化,在WOF[19]中,Zille等人将决策变量分成若干组,每个组都对应一个权重向量。借助权重向量把决策空间维度较大的多目标优化问题转换为决策空间维度较小的多目标优化问题,还有最近新提出的方法 LSMOF[20],与WOF不同,LSMOF采用双向权重向量,加快了种群收敛速度。但是此类型方法缺点是不考虑不同权重变量之间的差异,影响种群收敛速度。

种群的多样性和搜索的收敛能力在种群的搜索过程中起着十分重要的作用,本文提出一种两层优化辅助的大规模高维多目标优化算法(TOS-assisted LSMOEA).在第一层优化中,主要通过增加种群多样性提高算法的探索能力,因此选用具有良好探索能力的社会学习微粒群算法(SL-PSO)[21]算法进化种群,并且通过非支配解集保存种群进化过程中产生的非支配解。随后,在第二层优化策略中,根据参考向量选择若干非支配解进行遗传操作以提高算法的开采能力,以获得较好的非支配解集。

1 相关概念

1.1 社会学习微粒群算法(SL-PSO)

SL-PSO是针对于大规模单目标优化问题提出的一种改进微粒群算法。与其他单目标微粒群优化算法相比,由于它采用随机选择较好个体的对应维度学习,而并非最好个体,增强了算法的多样性,提高了算法的全局搜索能力,因而在解决大规模优化问题上获得了较好的结果。在SL-PSO中,每个个体的学习如式(2)所示:

Xi,j(t+1)=

(2)

式(2)表示如果个体i在第t代的学习概率pi(t)小于给定的学习概率,则个体i进行学习,否则不变。Δxi,j(t+1)的更新如式(3)所示:

ΔXi,j(t+1)=r1(t)·ΔXi,j(t)+

r2(t)·Ii,j(t)+r3(t)·Ci,j(t)

(3)

式中:ΔXi,j(t+1)由三部分组成,第一部分中ΔXi,j(t)表示个体i在t代第j维的速度;第二部分中Ii,j(t)表示个体i的第j维向比个体i适应值好的任意个体k的第j维学习;第三部分中Ci,j(t)表示个体i向所有个体第j维的均值学习,r1(t),r2(t),r3(t),为3个随机数。Ii,j(t)和Ci,j(t)具体式(4)所示:

(4)

1.2 遗传算法

遗传算法(genetic algorithm,GA)是一种模拟自然界生物的物竞天择,适者生存和通过染色体产生子代的智能算法。该算法通过群体搜索技术和种群之间反复迭代逐步寻优到全局最优解,其中在产生子代时算法的交叉和变异算子起着十分重要作用,本文采用模拟二进制交叉策略和多项式变异策略来产生子代种群。

1.2.1 模拟二进制交叉

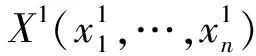
(5)

式(5)中,β是由分布因子η按照公式动态随机决定,如式(6)所示:

(6)

1.2.2 多项式变异

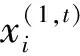
(1)选择随机数ui∈[0,1);

(2)计算βi的值:

(7)

其中,ηu为实验中设置的非负实数。

(3)计算子代:

(8)

1.3 支配关系

假设给定两个个体x,y,如果同时满足式(9),则称x支配y,记为xy

∀i∈(1,2,…,M)∶Fi(x)≤Fi(y)∧

∃i∈(1,2,…,M)∶Fi(x)

(9)

式中:Fi(x)为个体x的第i个目标函数值,M为目标函数的个数且i∈(1,2,…,M).

2 两层优化策略的优化算法(TOS-assisted LSMOEA)

算法的流程:

输入:种群数量N,初始种群P,最大评价次数Fitmax;输出:非支配解集A

(1)在决策空间中随机取N个点,构成初始种群P;

(2)把初始种群中的非支配解保存于集合A中;

(3)使用SL-PSO更新个体位置的方法产生新的种群,并计算目标函数值。(详见2.1节);

(4)更新非支配解集A;

(5)从A中选择若干个体进行遗传操作,并计算目标函数值。(详见2.2节);

(6)更新非支配解集A;

(7)若未达到最大评价次数,则返回3,否则,进入下一步;

(8)优化结束,输出集合A中的解。

2.1 第一层优化策略

采用基于个体适应值差值[23]作为单一指标用于对个体进行排序,其计算方法如下:

(10)

式中,fp(i)表示个体p在第i个目标上的目标函数值。M表示待优化问题目标个数。

然后利用SL-PSO的位置更新方式对个体进行位置更新。即每个个体的每一维度随机选择一个种群中比自己优秀的个体进行学习,同时由于非支配解集A中保存着进化过程中产生的优秀个体,因此种群中的个体还有一定的概率r(r=0.1)向集合A中的个体学习。为了避免种群陷入局部最优,所以种群中的个体不再向每一维度的均值学习。

在第一层优化中,个体的速度学习如式(11),其中r1,r2为0～1之间的随机数,t表示代数,Xi,j(t)表示个体i的第j维在第t代的值。k(i

vi,j(t+1)=(0.5*r1+0.1)*

vi,j(t)+r2*(Xk,j(t)-Xi,j(t))

(11)

Xi,j(t+1)=Xi,j(t)+vi,j(t+1)

(12)

2.2 第二层优化策略

第二层优化中主要考虑提高算法的收敛能力,主要分为两步。

(1)选择父代种群:当非支配解集A中的解的个数小于等于N时,A中的解全部作为父代种群。当非支配解集A中的解的个数大于N时,在目标空间生成均匀分布的N个参考向量,依据式(13)计算个体和参考向量之间角度:

(13)

其中λj表示参考向量,f(Xi)表示个体i的目标向量,θxi,λj表示个体i的目标向量和参考向量j之间的角度。每个参考向量选择和自己目标向量角度最小的解,并把所有选出来的解作为父代种群。由于该部分种群是由非支配解集中的解组成,因此具有较好的收敛性。

(2)通过GA产生子代种群:当选出父代种群之后,该种群将通过遗传算法产生子代种群,对其进行目标函数评价,并更新非支配解集。

3 实验

为了验证本文算法的有效性,本文选择被广泛采用的MaF[24]函数测试集上进行测试,MaF的决策空间维度为500,分别在3,5,8,10个目标上进行了测试。

3.1 实验设置

为了说明本文提出算法的有效性,选NMPSO[25],MPSOD[26],RVEA[8],MaOEACSS[12]4个算法作为对比算法。最大评价次数为10 000.种群规模大小的设置见表1,其他参数设置见表2.其中w为权重系数,c1,c2为学习公式系数,pc,pm,ηc,ηm分别为交叉概率,变异概率,交叉分布指数,变异分布指数,CR为交叉率,F为差分进化算法中的收缩因子。

表1 TOS-assisted LSMOEA种群规模设置

表2 算法相关参数设置

本文实验中的所有算法在每个测试函数上均独立运行 20 次,IGD 的统计结果如表3,表4.其中最优结果值用加粗字体表示。采用显著水平为0.05的Wilcoxon 秩和检验,从统计学角度比较了算法之间差异的显著性,表中“+”“-”和“≈”分别表示其他对比算法明显优于、明显劣于和近似于本文提出的算法。

表3 500维MaF1不同策略对比分析

表4 TOS-assisted LSMOEA与MPSOD,NMPSO,RVEA,MaOEACSS在 500维MaF 函数上IGD 值比较结果

3.2 算法性能度量指标

本文选取反向世代距离[27](Inverted Generational Distance,IGD)作为性能度量指标来评价解集的收敛性和多样性。P*为真实的PF面产生的解的集合,S为EMO产生的解的集合,S中IGD如式(14)所示:

(14)

式中,dist(X*,S)为P*中的点X*和邻域S之间的欧氏距离。IGD越小表示S中的解越接近真实的PF面,解集S的质量越好。

3.3 算法参数及策略分析

为了提高算法搜索效率,本文中种群有一定的概率向非支配解集A中的个体学习。分别测试了当r为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9时算法在MaF1测试函数500维时的表现,实验结果如图1所示。可以看出,当r取0.1时算法在各个目标上的表现是最好的,因此本文r取0.1.

图1 500维MaF1 参数r对比分析

本文采用两层单独优化,说明提出的两层优化策略的有效性,策略1为算法仅进行第一层搜索,策略2为算法仅进行第二层搜索。在MaF1测试函数500维进行测试。

为了验证提出的算法中第一层搜索可以改善非支配解集的多样性,进行了对比实验,如图2所示。

图2 MaF1和MaF6测试函数500维10个目标上指标分布图

图2展示了不同策略在MaF1以及MaF6测试函数500维10个目标上种群进化过程中非支配解集多样性和收敛性指标的变化图。为了便于观察,在图2中横坐标上收敛性指标取了相反数。收敛性指标的计算如式(15):

(15)

多样性指标的计算如式(16):

(16)

式中,dist(Xi,Xj)表示点Xi和点Xj之间的欧式距离。A为非支配解集。

多样性指标值越大说明算法的多样性越好,收敛性指标的值越小说明算法的收敛性越好。从图2中可以看出,在收敛性相同的情况下,TOS-assisted LSMOEA算法的多样性优于TOS-assisted LSMOEA变种(即仅采用TOS-assisted LSMOEA算法中的第二层搜索)。因此,本算法中第一层搜索可以有效的提升算法的多样性。

3.4 实验结果及分析

表4展示了本文提出的算法和4种对比算法在MaF测试函数500维的IGD测试结果。可以看出,本算法和其他4种对比,表现差,表现好和没有显著性差异的分别为12/37/3,12/36/4,13/36/3,14/34/4.可以发现本算法对于解决大规模高维多目标优化问题是有效的。

4 总结

本文提出了一种两层优化策略用于求解大规模高维多目标优化问题,在第一层优化中,采用多样性较好的SL-PSO位置更新方式引导种群进化,并用于更新非支配解集。随后在第二层优化中,依据个体和参考向量之间的角度选择一部分个体组成父代种群,使用模拟二进制交叉和多项式变异策略产生子代种群以提高算法的开采能力,评价后的子代同样用于更新非支配解集。MaF测试函数上的实验结果表明本文提出的两层优化策略在解决大规模高维多目标优化问题时是有效的。