数值模拟顶部籽晶溶液生长法制备单晶碳化硅的研究进展

隋占仁,徐凌波,崔 灿,王 蓉,杨德仁,皮孝东,韩学峰

(1.浙江理工大学物理系,浙江省光场调控技术重点实验室,杭州 310018;2.浙江大学杭州国际科创中心,浙江省宽禁带半导体重点实验室,杭州 311200;3.浙江大学材料科学与工程学院,硅材料国家重点实验室,杭州 310027)

0 引 言

宽禁带半导体材料碳化硅(silicon carbide, SiC)凭借着其高击穿场强、高热导率、高饱和电子迁移率、高化学稳定性、抗辐射等性能,在电力电子器件领域拥有广阔的发展前景。尤其是在高温、高频、高功率等应用场景下有着得天独厚的优势[1-3],其优异的性能使得SiC在半导体材料市场上受到广泛青睐,以SiC为代表的宽禁带半导体材料对国民经济和国防军工的发展具有重要意义,并已获得国家的高度重视与大力支持[4]。为成功实现SiC在相关领域的大规模应用,制备高质量、大尺寸的SiC单晶衬底是必不可少的。当前主流的SiC单晶制备方法是物理气相传输(physical vapor transport, PVT)法、高温化学气相沉积(high temperature chemical vapor deposition, HTCVD)法和顶部籽晶溶液生长(top-seeded solution growth, TSSG)法,其模型如图1所示。其中PVT法在这几种方法中占据主导地位[5],虽然目前国内外PVT法制备6英寸(1英寸=2.54 cm)的SiC单晶衬底已经实现了产业化[6],国外直径8英寸的单晶衬底也正在迈入产业化阶段。但是PVT法制备SiC单晶仍然面临着很多问题,如SiC单晶位错密度较高(约为102～104cm-2)[7]、扩径难度大、成品率低,以及高纯SiC粉体获取困难等[8-9]。不同于PVT法,TSSG法是从溶解C的硅熔体中生长SiC单晶的方法。这种方法生长SiC晶体是在接近热平衡的条件下进行的,其低生长温度和接近热力学平衡的条件会使得晶体质量显著提高[10],适合制备高质量的SiC晶体。不仅如此,TSSG法制备SiC还具有生长过程可调控性强、易扩径、易实现p型掺杂等优势。基于TSSG法这些独特优势,近年来对该方法的研究日趋增多。

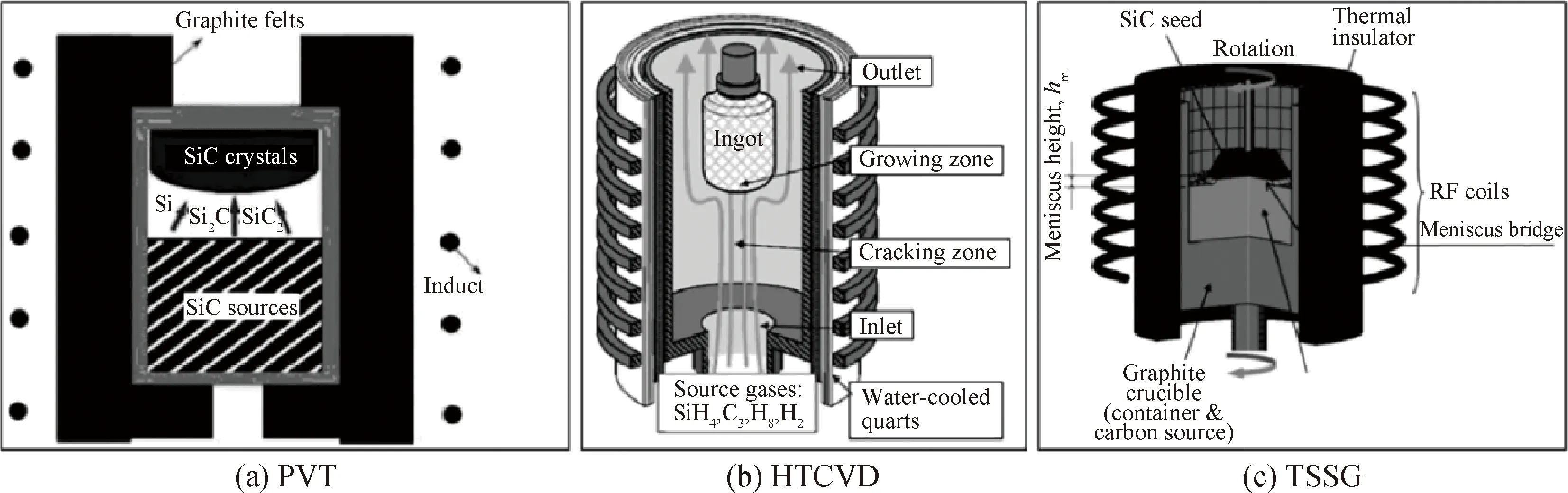
图1 三种SiC单晶生长技术的模型示意图[11]Fig.1 Schematic diagram of three methods for SiC single crystal growth[11]

利用计算机对TSSG法进行数值模拟研究是这些研究中非常重要的一环,对内部现象的探究及指导实际生产都有非常重要的意义。本文首先回顾TSSG法生长SiC单晶及相关数值模拟分析的发展历程,接着简要介绍TSSG法生长SiC单晶及数值模拟的基本原理。然后根据目前研究进展分别介绍了数值模拟计算分析TSSG法生长SiC单晶模型涉及的主要模块、影响单晶生长的主要因素(如马兰戈尼力、浮力、电磁力等)和TSSG法生长SiC单晶数值模型的优化方法。最后,指出了数值模拟TSSG法生长SiC单晶在未来的研究重点并进行总结。

1 数值模拟分析TSSG法的发展历程

大多数半导体单晶都可以从熔融状态或溶液中生长出来,但SiC本身的特性使其难以利用这种方法生长出单晶。计算结果显示,化学计量比的SiC只有在压力达到105atm、温度达到3 200 ℃时才能熔融[12],这样苛刻的生长条件很难在工业上大规模应用。虽然液相法生长半导体单晶研究历史悠久(20世纪60年代Halden等[13]就第一次使用液相制备出SiC单晶),但很长一段时间业界一直将PVT法制备SiC晶体视为标准方法,对液相法生长SiC晶体的研究一直较少[14-16]。尽管研究者们在PVT法生长SiC研究方面取得了显著的进展,但PVT法生长的SiC晶体仍存在大量的缺陷,如微管、位错和寄生多型体等[17]。时至今日,PVT法生产的SiC晶体位错仍较多[18],严重影响器件性能[19-21]。意识到此问题后,研究者们便逐渐将注意力转移到液相法上来。与PVT法相比,液相法生长SiC单晶的优点是生长条件接近热平衡,缺陷在晶体生长过程中横向传播,因此可以产生更高质量的晶体[22-23],Murayama等[24]研究表明,相较于PVT法,使用TSSG法可将所有类型缺陷的密度降低两个数量级。近10年来,TSSG法生长SiC单晶取得了不错的进展,籽晶尺寸也在不断扩大,图2给出了近年来TSSG法获取的典型大尺寸SiC单晶及其直径与厚度。

TSSG法生长SiC单晶是在高温、半封闭的环境下进行的,且内部溶液不透明,导致研究者很难通过原位观察获得生长过程中内部高温溶液、籽晶等重要区域的状态信息,现有手段也很难在不影响炉内生长的前提下对炉内状态进行监测。除此之外,只有对大量的实验数据进行研究整理才能有效地对模型进行优化。但现实中这点是不容易实现的,一方面是由于TSSG法生长SiC单晶是非常缓慢的过程,获得足够多的数据需要耗费大量时间。另一方面则是实验模型的改进成本较高,细微的改动可能需要将整个装置重新制造和安装。而且根据研究需要,这种对设备的调整通常是持续多次的,会耗费大量人力、物力和时间成本。另外该过程中还可能由于环境改变等不可控因素对实验结果产生一些未知影响。这些问题都极大制约了研究者们对TSSG法内部机理的探索,限制了TSSG法生长SiC单晶的发展。随着计算机技术与模拟计算技术的发展,研究者们发现利用计算机可以模拟出整个实验过程中炉内的状态变化,并直观地将结果展示出来。事实也证明,应用该技术可以大幅降低研究者们探究TSSG法生长机理的难度。

目前数值模拟分析已成为材料科学研究与工程研发的必备工具,对晶体生长模型的优化起到十分重要的作用[30]。数值模拟TSSG法生长SiC单晶的主要工作是利用数值模拟计算程序模拟出TSSG法生长SiC单晶过程中内部模块产生的变化。首先在计算机上搭建好拟研究的TSSG生长炉模型,并设置好初始条件、边界条件、控制方程等。然后开始计算,利用计算机求解出相应的控制方程,模拟出单晶生长过程中产生的现象,如熔体的流动、内部热场分布、浓度分布等。最后对所得结果进行分析并总结规律,利用得到的结论继续改进实验模型或指导实际生产,形成正反馈从而促进TSSG法生长SiC单晶的发展。针对TSSG法生长SiC单晶过程的数值模拟工作最早可追溯到2010年,Mercier等[31]对高温溶液法进行了系统的建模研究,研究内容涵盖了温度梯度、坩埚结构、电磁对流、马兰戈尼力等不同因素对传热和对流的影响。图3是Mercier团队使用的数值模型的结构图,其主要由感应加热器、基座、绝热石墨毡和内部石墨坩埚(作为高温溶液的容器和C源)等部分组成。

2013年,Kusunoki等[27]在炉子内部加入了浸没导向器(immersion guide, IG),并对改进后的新装置进行了数值模拟计算研究,图4展示了加入IG装置后的生长炉模型与其流场的数值模拟结果,研究证明在炉内加入IG装置会使得溶液中产生更均匀的流动,更利于SiC单晶的高质量生长。2014年,作者又在此基础上进行了更深入的研究[32],他们发现通过选择合适的IG形状,有利于籽晶下方区域形成更均匀的向上流动,对生长高质量的SiC单晶十分有利。作者还计算了不同IG条件下单晶的生长速率,与实验吻合较好。最终通过选取最佳形状的IG装置对内部溶液进行控制,成功生长出直径为3英寸、厚度为4 mm的4H-SiC晶锭。

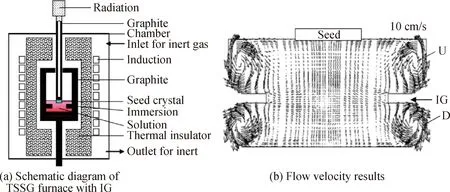
图4 Kusunoki的改进模型[27]Fig.4 Kusunoki’s improved model[27]

2016年,Umezaki等[33]通过对TSSG法生长SiC单晶进行全局计算流体动力学(computational fluid dynamics, CFD)模拟,发现使用TSSG装置进行SiC单晶生长期间,随着籽晶转速的增加,生长速率显著提高。同年,韩国Ha等[34]基于有限元分析(finite element analysis, FEA)计算了TSSG法中硅熔体的温度分布、速度场和C浓度分布,其计算结果表明不同热场对C浓度分布会造成显著差异,且晶体附近的小温度梯度更有利于SiC晶体的稳定生长。还有一些研究主要是针对坩埚的改进,如Mukaiyama等[35]、Choi等[36]与Horiuchi等[37]分别对坩埚的形状、内表面形貌、尺寸及旋转速度等方面做出了研究,为TSSG法生长更高质量SiC单晶提供了一些新的优化思路。最近几年,随着人工智能(artificial intelligence, AI)技术的发展,将晶体生长与现代人工智能技术相结合的研究也逐渐增多。如Wang等[38]利用强化学习(reinforcement learning, RL)模型,优化TSSG法生长SiC晶体过程中的熔体流动,从而以更高的速率生长更均匀的SiC晶体。2021年Yu等[39]利用机器学习技术,加快了对坩埚模型几何形状优化的进程。作者将机器学习技术与遗传算法结合,在较短的时间内从大量备选的坩埚参数中获得了最佳参数配置,其使用的TSSG模型和神经网络示意图如图5所示。基于此设计出了最佳生长系统,成功制备了直径150 mm的SiC单晶。这些针对TSSG系统的创新工作对指导实际晶体生长,获得质量更高、生长速度更快的SiC单晶有着重要意义。

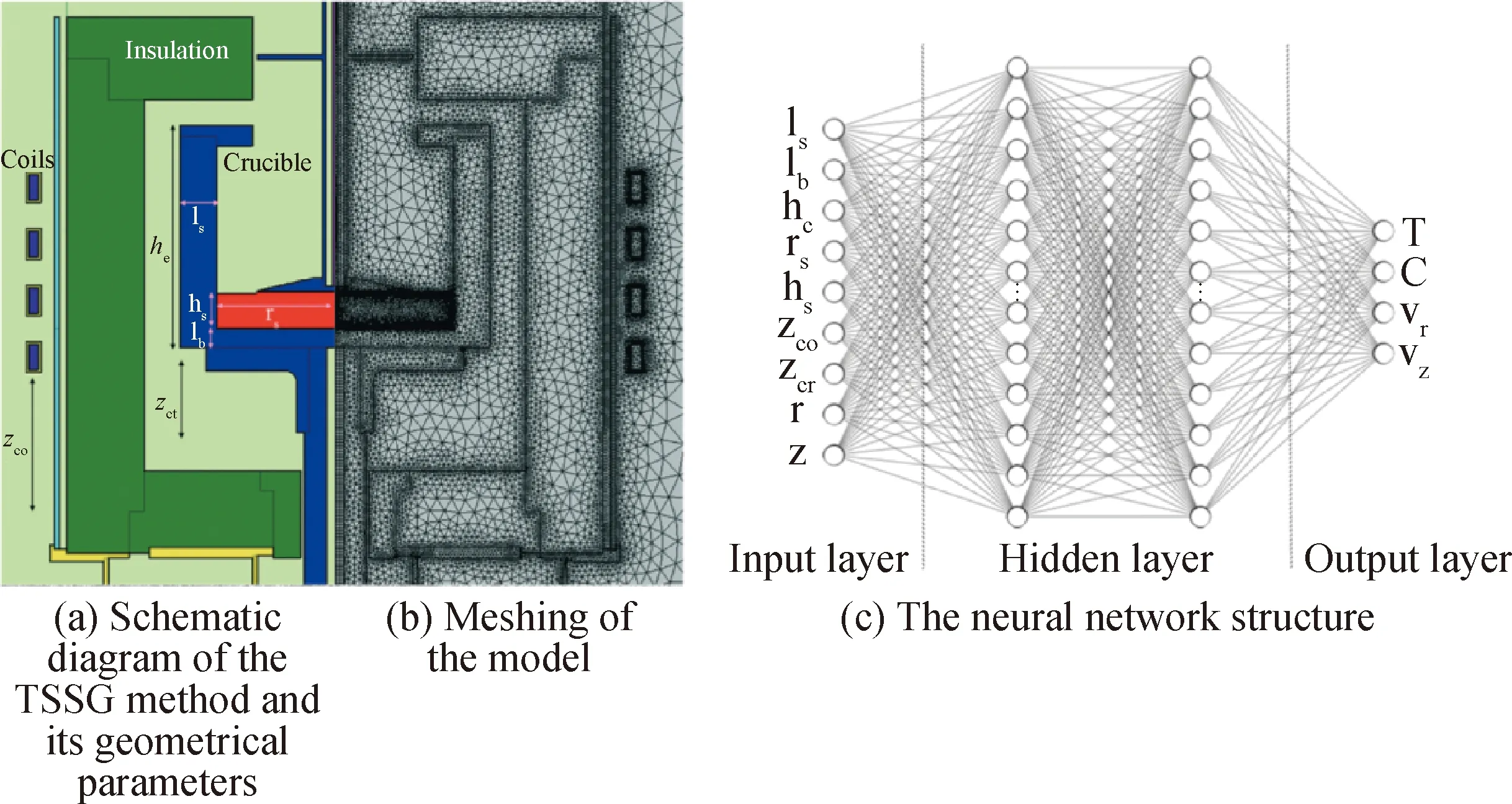
图5 Yu的模型示意图[39]Fig.5 Schematic diagram of Yu’s model[39]

2 数值模拟分析TSSG法的基本原理

TSSG法生长SiC单晶常见的生长炉模型如图1(c)所示,其主要结构由外部感应加热线圈、石墨保温毡、同时当作高温溶液容器和C源的高纯度石墨坩埚、高温熔体、SiC籽晶和悬杆构成。进行SiC单晶生长时,先用感应线圈加热坩埚至原料完全熔融。通常将炉内温度范围控制在1 700～2 100 ℃,等稳定的温度场形成后,高温溶液中C的浓度达到平衡,将带有籽晶的悬杆从顶部缓缓浸入高温溶液。生长时,通过控制温场使高温溶液在轴向上产生图6所示的温度梯度。由于温度梯度的存在,坩埚顶部和底部的C的溶解度不同:上方靠近籽晶处温度较低,C溶解度较低;下方温度较高,C溶解度则较高。底部达到C饱和的熔体流到温度较低的籽晶附近后,溶液中过饱和的C结合高温溶液中的Si就可以在籽晶表面上生长出SiC单晶(溶解的C由石墨坩埚源源不断地供应)。当过饱和部分的C析出后,溶液随着对流回到坩埚壁处的高温区域,并再次从石墨坩埚处溶解C,形成饱和溶液。整个过程循环反复进行着SiC单晶的生长[40]。该过程中炉内的温度梯度是晶体生长的根本驱动力,影响着溶液流向及C的浓度分布。另外,C在纯硅中的溶解度很低(在实验温度范围内溶解度通常小于0.1%[41]),提高高温溶液的C浓度是快速生长SiC单晶所必需的,因此研究者经常在坩埚内添加Cr、Ti、Y等金属助溶剂以增加C在硅熔体中的溶度[42-43]。

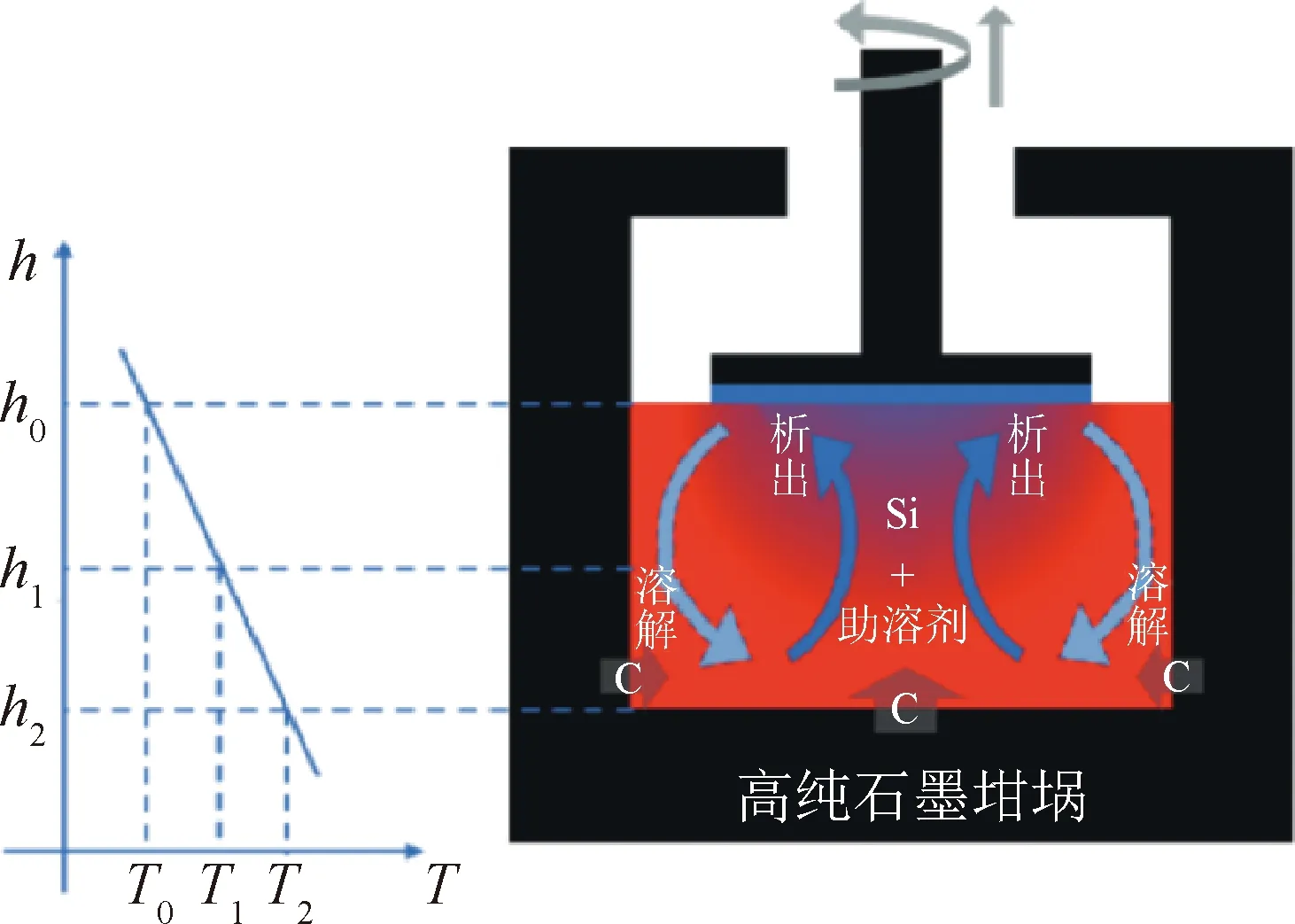
图6 TSSG法生长SiC单晶示意图[11]Fig.6 Schematic diagram of growing SiC single crystal by the TSSG method[11]

对TSSG法生长SiC的数值模拟主要方法是利用有限元程序对上述SiC单晶的生长过程进行仿真。其一般步骤是在有限元软件里搭建好TSSG生长炉的几何模型,如模型的基本几何形状、坩埚形状和尺寸、籽晶大小等。然后根据研究内容设置模型的初始条件、边界条件、各种材料的物理属性及控制方程,再对建好的模型进行网格划分。计算时有限元软件会将系统的求解区域根据划分的网格离散成一个个小单元的分组体系,把一个连续的无穷自由度问题变为离散的有限自由度问题,最后利用计算机求解[37-39,44]。目前很多研究组进行了TSSG法生长SiC晶体的建模仿真工作,并取得了不错的成果。图7所展示的是一些研究小组所建立的TSSG法生长SiC的典型数值模型。

图7(a)是Ujihara等[45-47]建立的一种比较经典的TSSG生长炉模型,该模型被用于探究马兰戈尼对流、静磁场、籽晶旋转等因素的影响,对后来研究有很高参考价值;图7(b)是Park等[46]利用数值模拟的方法研究石墨坩埚辐射率对温度分布的影响时所使用的模型,左半侧展示的是该模型的几何图形,右半侧展示的是网格划分;图7(c)展示的是Mercier等[47]的计算模型,其特点是相较于其他模型,内部多了电阻加热装置,来获得适合的温度梯度。

3 对流与传热模块

TSSG法生长SiC单晶的数值模拟主要分为流动、传热和传质三个模块,其中对流与传热模块是TSSG法生长SiC单晶模型中最基础、最重要的模块,模型内部良好的流场与温度场是实现TSSG法生长SiC单晶的关键[11]。对传热与流动进行数值模拟计算研究旨在计算出系统的温度场和Si熔体的流场分布,加深研究者对熔体内部传热传质现象理解,从而根据计算结果对实验设计加以改进。如Mercier等[31]证明了马兰戈尼力和电磁力对溶液生长过程失稳的重要性;Ujihara等[45]通过数值模拟给出了TSSG法生长SiC单晶过程中各种力对SiC单晶生长影响大小的排序为:表面张力>电磁力>离心力、浮力;Ha等[34]通过数值模拟计算和实验结合,证明了在晶体和熔体之间的界面附近小温度梯度的热区结构会使TSSG法生长的SiC晶体更加稳定。Lefebure等[49]揭示了浓度场和对流模式之间的直接关系,强调了对流在C传输中的重要作用。TSSG法生长SiC单晶过程中熔体内传热和流动现象由连续性方程、动量守恒和能量守恒方程所控制,它们是进行模拟计算的主要理论依据。方程如下[50]:

连续性方程:

(1)

动量方程:

(2)

能量方程:

(3)

式中:ρ是熔体密度;v是熔体速度;t是时间;p是压力;μ是熔体动力粘度;βT是熔体热膨胀系数;T是熔体温度;T0是熔体中的最低温度;g是重力加速度;α是热扩散率。上述方程基于下列几个假设[34]:

1)生长熔体是一种不可压缩的牛顿流体。

2)C溶解度低,不考虑溶质对流。

3)熔体内温差足够小,可运用Boussinesq近似。

4)动态界面变形(由于熔体中的对流)可忽略不计。

在实际的数值计算中可能会根据实际模型对上述方程进行适当调整,但原理基本类似。表1列出来的是计算时使用的高温溶液的参数;图8展示的是TSSG法生长SiC晶体时,坩埚中高温溶液流场和温度分布的模拟结果。

表1 TSSG法数值模拟中使用的高温溶液物理特性Table 1 Physical properties of the solutions used in numerical simulation of the TSSG method

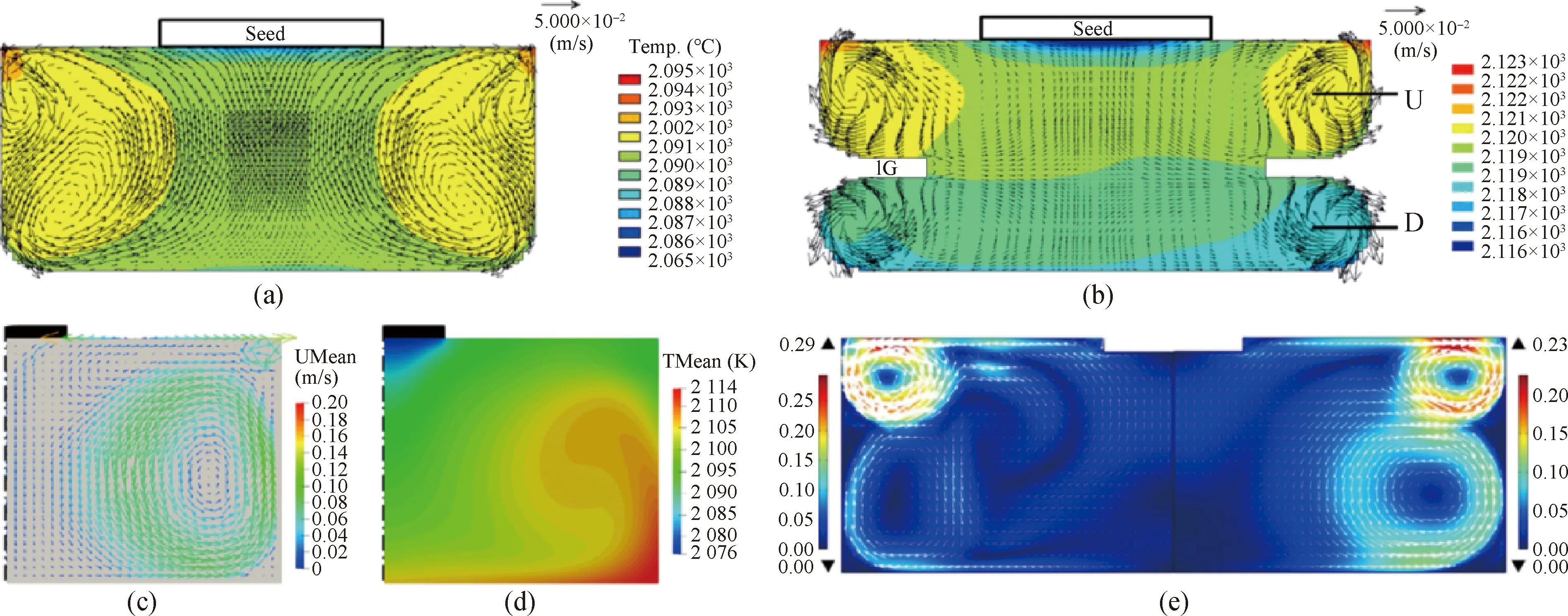
图8 不同类型坩埚内溶液的温场与流场分布。(a)不含IG导流器的流速和温度分布[32];(b)含IG导流器的流速与温度分布[32];(c)流场模拟结果[45];(d)温场拟结果[45];(e)相同模型不同隔热层设计下的流场与温场分布(左:短隔热层结构,右:长隔热层结构)[34]Fig.8 Flow velocity and temperature distribution of melt in different crucibles. (a) Flow velocity and temperature results without IG[32]; (b) flow velocity and temperature results with IG[32]; (c) flow velocity results[45]; (d) temperature results[45]; (e) flow velocity and temperature results of different insulation structure (left: short insulation structure; right: long insulation structure)[34]

从图8中可以看出,在TSSG生长过程中,使用不同类型的坩埚,内部溶液的流向也不相同。高质量晶体生长的条件包括溶液内部均匀的流动和籽晶下方自下向上的流动。这种流向可将坩埚底部的C浓度高的溶液更快地输运至籽晶表面,实现SiC单晶在顶部籽晶表面快速析出。迄今为止,针对数值模拟中基础的流动与传热模型的优化主要集中在以下几个方向:炉内温度控制、坩埚旋转及形状、籽晶旋转与提拉技术。下面将针对这几方面的相关研究进行梳理与总结。

3.1 炉内温度控制

生长炉内部需要保持特定的温度梯度来保证含C溶液在籽晶表面析出(见图6),过大或过小的温度梯度或不合适的温度场设定都会对SiC单晶生长产生不利影响。如温度梯度过小会导致浮力对流不够强,不利于C从坩埚壁附近到籽晶表面的运输,晶体生长缓慢;梯度过大则会导致单晶生长不稳定、产生不稳定湍流[31,51]。不合理的温度场还可能会导致SiC晶体的表面粗糙,降低SiC晶体品质等[52]。为了获得更适宜的温度分布,研究者们做了很多尝试。如Lefebure等[53]进行了具有极低温度梯度的坩埚设计,极低轴向温度梯度用来提高晶体生长质量,如图9所示,极低的径向温度梯度用来避免浮力对流的任何失稳。研究发现对流在C从溶解区到结晶区的传输过程中起主要作用。

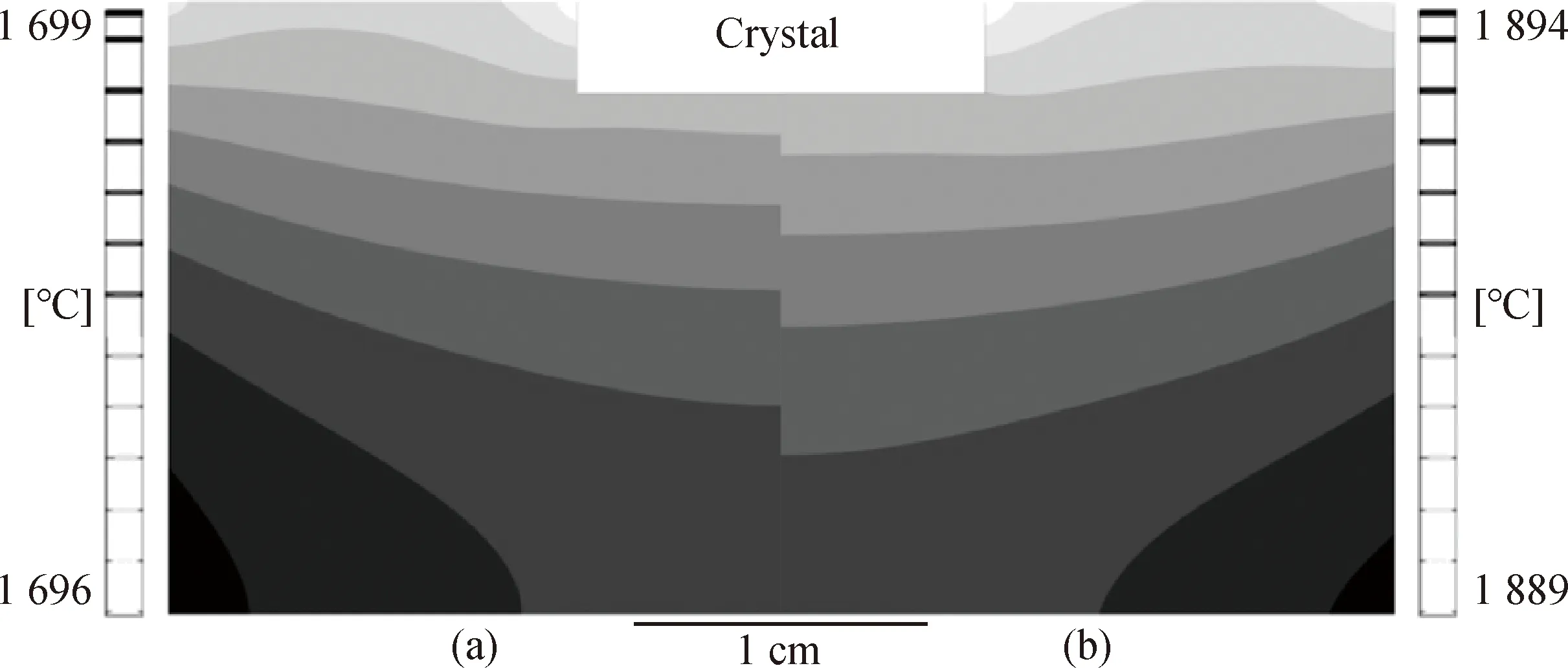
图9 低温度梯度模型在温度为1 700 ℃(a)和1 900 ℃(b)时的温场[53]Fig.9 Temperature results of low temperature gradient model in 1 700 ℃ (a) and 1 900 ℃ (b)[53]

2018年,Ha等[34]将普通TSSG生长炉的石墨隔热层增高,显著改变了生长炉的温度梯度。由于改进后的结构减少了垂直方向的热损失,使得坩埚获得了更小的温度梯度(不同模型温度分布如图10所示,其生长出的单晶对比如图11所示)[34]。实验结果表明,具有更小温度梯度的热场结构,尤其是在籽晶与高温溶液交界面附近区域的低温度梯度,有利于SiC晶体的稳定生长。2019年,该作者的另一研究[54]表明调整温区的孔径是精细控制熔体中温度梯度的有效方法,可获得更高质量SiC单晶。

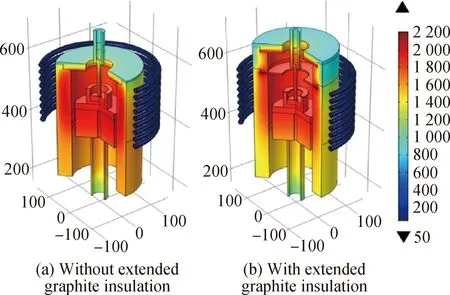
图10 生长炉的温度分布(单位:℃)[34]Fig.10 Temperature distribution of furnace (unit: ℃)[34]

Koike等[55]尝试了与传统温度场不同的非轴对称温度场,并进行仿真计算,如图12所示,发现在籽晶下方,溶液对流是非轴对称并且是单向的,而且籽晶附近的过饱和度溶液流动增大。利用这种非轴对称温度分布引起的非轴对称溶液对流,在TSSG法中获得了凸形晶体生长界面,该研究为TSSG法生长不同晶面形状提供了新的思路。

图12 Koike的非轴对称温度场模型[55]。(a)Si溶液模型示意图;坩埚壁(b)和坩埚底部(c)的非轴对称热边界条件Fig.12 Koike’s non-axisymmetric temperature distribution model[55]. (a) Schematic diagrams of Si solution;non-axisymmetric thermal boundary conditions of the crucible wall (b) and the crucible bottom (c)

3.2 坩埚旋转技术及形状调控

迄今为止,在TSSG法生长SiC单晶的研究中,与坩埚相关的优化主要集中在对坩埚形状、尺寸和结构的调整。坩埚的形状变化对温度、感应加热系统引起的洛伦兹力分布、流场、溶液中的C浓度和SiC的生长速率具有显著的影响[35],坩埚旋转则主要导致流场的变化进而影响SiC单晶生长。利用数值模拟计算技术可以更深入探索坩埚的形状、结构、旋转等因素对晶体生长的影响。Mercier等[31]为了避免马兰戈尼力产生的流动对晶体生长的不利影响,设计出减少自由表面尺寸的向内倾斜型坩埚模型并进行了仿真,发现倾斜坩埚在晶体生长稳定性、持续时间和液体自由表面的寄生成核等方面都有更好表现。Choi等[36]为了研究坩埚形状对温度梯度及C浓度分布的影响,对坩埚形状进行了改进和模拟分析,经其改进后的坩埚为阶梯壁式设计,具有连续的锯齿形状,如图13所示,该设计显著改变了温度梯度并提高了溶液中的C浓度,证实了阶梯坩埚结构有利于提高SiC晶体的生长速率。Liu等[56]认为影响TSSG法稳定生长大尺寸晶体的原因是随着坩埚尺寸的增大产生的感应加热不均匀,从而导致溶液流动不利于晶体生长。作者通过改进坩埚形状,建立了新的TSSG模型(模型见图14)并进行数值模拟。模拟结果表明,通过合理调整新坩埚模型的下层半坩埚的高度H1和宽度L1,可以实现大尺寸(4英寸)碳化硅锭的相对稳定生长。Yoon等[57]考虑到溶液中溶解的C由石墨坩埚提供,通过对坩埚表面进行粗糙化,促进了坩埚壁处C的溶解,有效地提高了SiC单晶的生长速率。

图13 Choi的生长炉模型示意图[36]Fig.13 Schematic diagram of Choi’s furnace model[36]

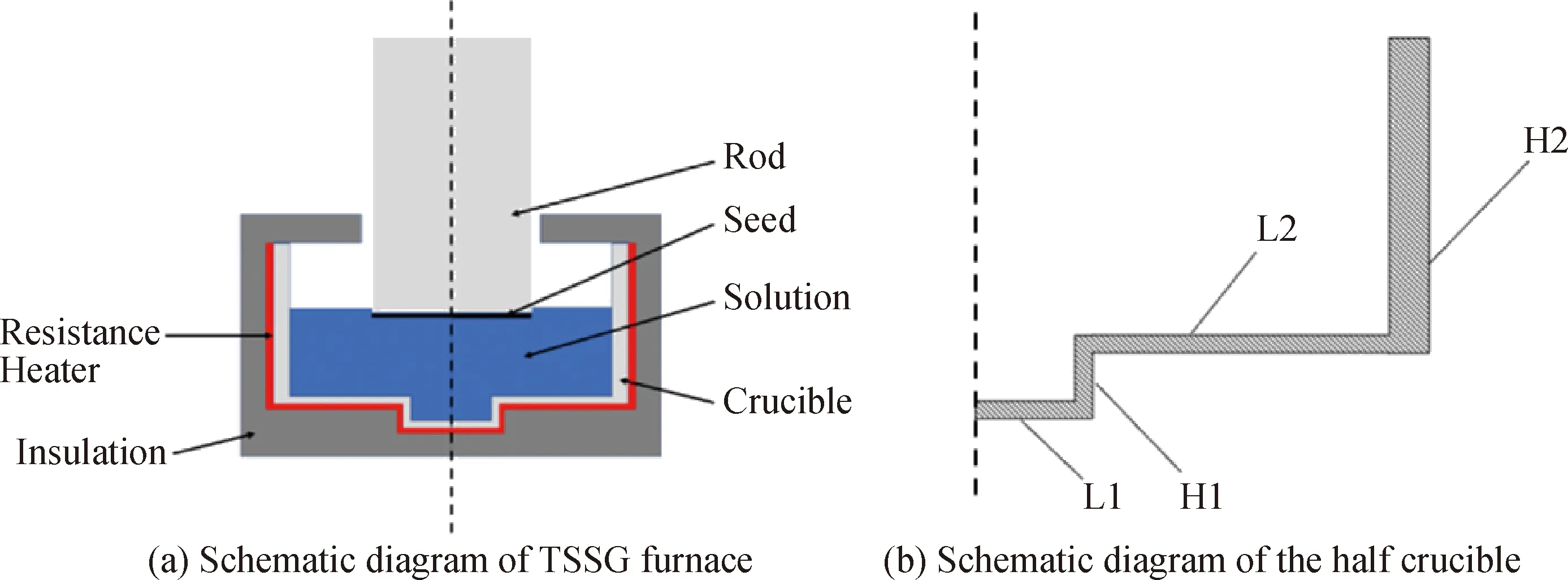
图14 Liu对坩埚形状的改进模型[56]Fig.14 Liu’s model of adjusted crucible shape[56]

加速坩埚旋转技术(accelerated crucible rotation technique, ACRT)是一种在晶体生长过程中按照一定的规律变速旋转坩埚,从而在液相中引入强制对流的技术,被广泛利用在晶体生长领域[58-59]。为了提高生长速度,Kusunoki等[60]使用ACRT在Si-Ti-C溶液里生长SiC单晶。作者研究了ACRT强制对流对生长速率的影响并对生长过程中的流体流动进行了数值模拟。结果表明,ACRT技术不仅显著提高了SiC晶体生长速率,还改善了籽晶表面的均匀性。

3.3 籽晶旋转与提拉技术

籽晶的旋转会影响籽晶与液面接触面附近的溶液流动,进而影响SiC晶体生长。2016年,Umezaki等[33]通过对TSSG法生长SiC单晶模型进行CFD模拟,计算了籽晶在不同旋转条件下溶液中的动量、热量和传质现象。其计算结果表明,籽晶的旋转会导致生长界面下方的不流动溶液层强制流动而使得该层变薄,导致溶质C的浓度梯度增大,提高了SiC单晶生长速度。同年,Daikoku等[61]开发了一种称为凹表面溶液生长(solution growth on concave surface, SGCS)法的新技术,通过控制单晶生长过程中籽晶与液面的相对位置,讨论了籽晶浸入液面、籽晶面与液面平齐和籽晶在液面上方这三种情况。并对浸入、静态和拉伸这三种不同条件下的籽晶进行仿真,仿真结果与凹形、凸形籽晶生长的模型如图15所示。作者通过实验证明了SGCS生长技术有助于抑制严重的台阶聚束现象,大幅减少单晶中的溶剂夹杂物,可获得高质量的SiC单晶。

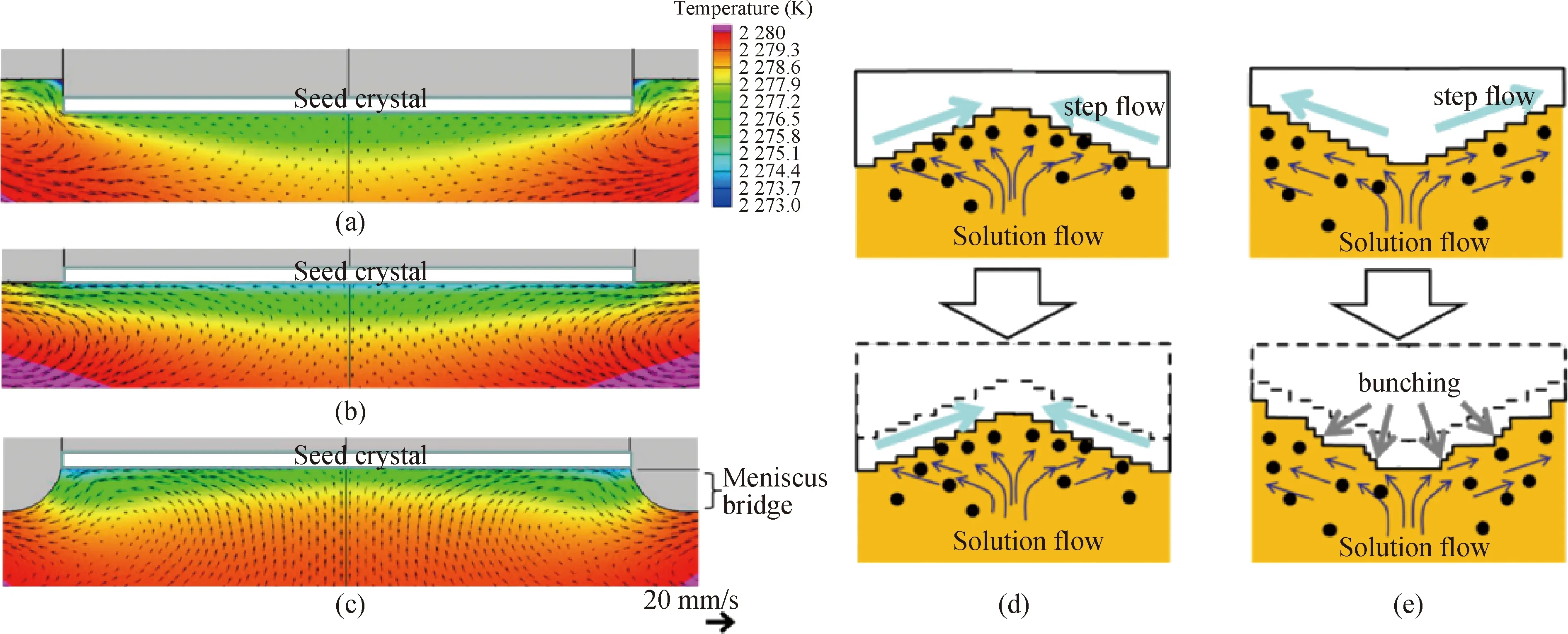
图15 籽晶与液面处于浸入条件(a)、静态条件(b)和拉伸条件(c)下溶液的温场和流场分布;籽晶附近溶液向上流动的条件下凹表面一直保持平滑(d),以及凸表面上由于方向相同的台阶流和溶液流引起的台阶聚束现象(e)[61]Fig.15 Temperature and flow velocity results indipping condition (a), static condition (b), pulling condition (c); the concave surface has been maintained smooth (d), convex surface has giant step bunching caused by the same direction for the step flow and solution flow (e) under the condition of upward flow of solution at seed crystal[61]

Yamamoto等[45]也对提拉籽晶对晶体生长的影响进行了数值模拟研究。不过他们侧重的是籽晶提拉高度变化所引起的高温溶液表面形状变化对SiC单晶生长带来的影响。该研究通过控制提拉杆改变了液面形貌。数值模拟结果如图16所示,在0.5 mm和1 mm拉力导致的表面变形情况下,熔体中的温差略有增加。但相较于其他影响因素如浮力、马兰戈尼力、电磁力等,该因素对晶体生长影响效果不明显。

4 基本模型的改进——加入马兰戈尼力、电磁力

很多研究已经证明,对TSSG法生长SiC单晶进行模拟时,熔体流动存在4种主要的对流:浮力对流、强制对流、电磁对流和马兰戈尼对流[45,49,61]。液体表面的马兰戈尼力与外部加热线圈所产生的电磁力都是引起坩埚内熔体对流的重要因素。与浮力对流、强制对流相关的温度、坩埚等设计在前文已作出阐述。本节主要探讨马兰戈尼力与电磁力对TSSG法生长SiC单晶的影响,以及利用数值模拟方法对这些因素的调控研究。

马兰戈尼效应是指在流体自由表面,因为表面张力梯度而造成的传质现象。表面张力不同的液体在一起会产生表面张力梯度,表面张力大的液体对其周围表面张力小的液体会产生拉力,液体会从表面张力低处向张力高的方向的流动[62-63]。在TSSG法生长SiC的模型中,马兰戈尼效应主要与坩埚内径向温度梯度、助溶剂掺杂、流体流场等因素有关。它可能会在熔体内部产生不利于生长的湍流,对单晶生长影响明显。利用数值模拟的方法对TSSG法生长SiC单晶的马兰戈尼效应进行仿真可以很直观地观察其产生的影响。Yamamoto等[45]重点对TSSG法中马兰戈尼效应进行了研究,使用的完整计算模型如图7(a)所示。作者在坩埚底部和侧壁上使用了无滑移边界条件,在自由表面使用了马兰戈尼对流的边界条件,在环境温度2 000～2 200 ℃条件下进行了模拟计算。图17、图18分别展示了考虑马兰戈尼力与忽略马兰戈尼力的流场、温度场、浓度分布在达到平衡时的计算结果。

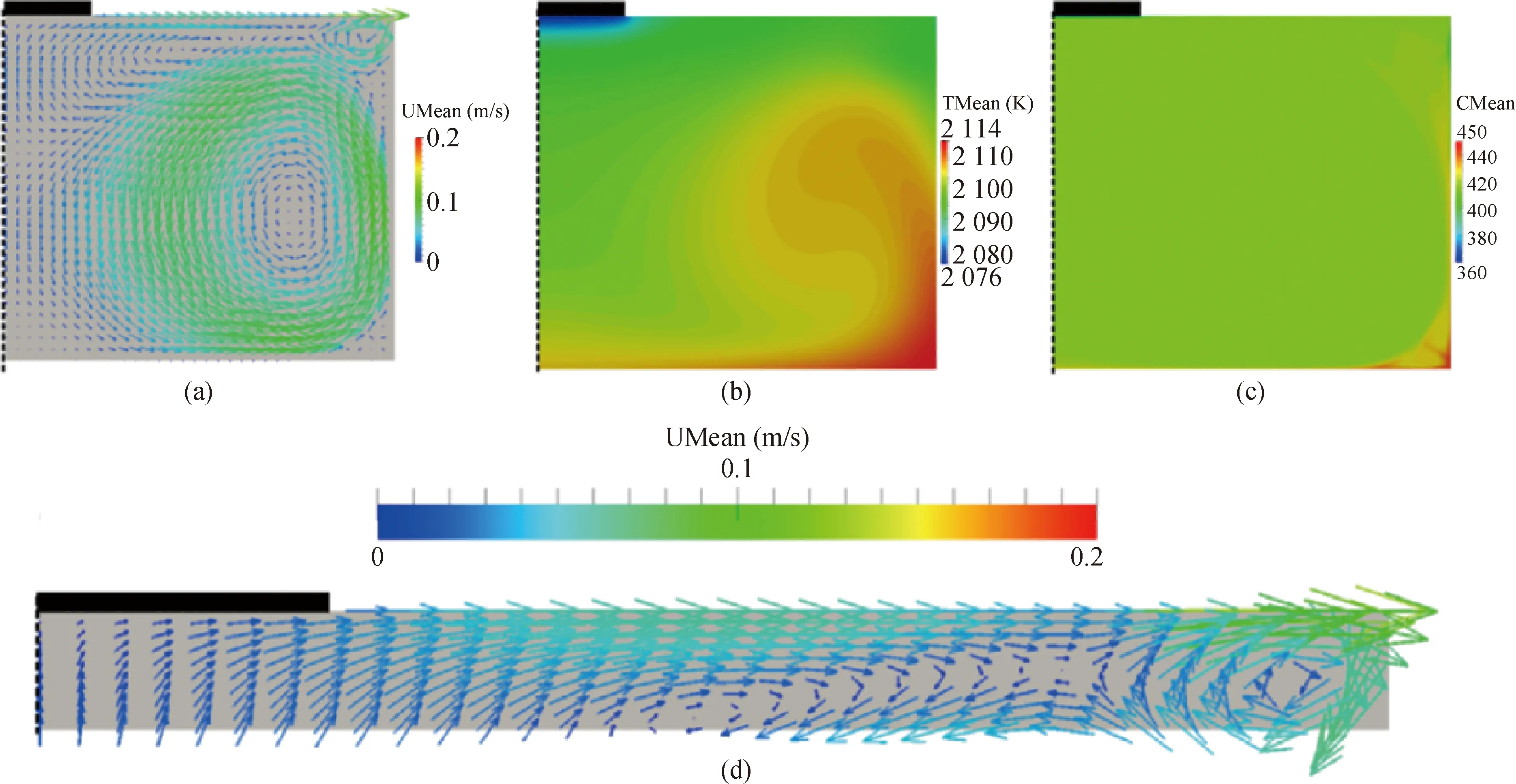
图17 忽略马兰戈尼效应时的流速分布(a)、温度分布(b)、浓度分布(c),以及自由表面附近区域流速分布细节图(d)[45]Fig.17 Flow velocity (a), temperature (b), concentration (c), and a closed-up view of the flow velocity along the seed and the free surface (d) in the case of flat free surface in the absence of the contribution of Marangoni convection[45]

从图17(a)可以明显看出,未考虑马兰戈尼效应时,籽晶轴向的熔体流向是向上的,有利于将高浓度的含C溶液输运到籽晶表面,可促进SiC单晶生长。而引入马兰戈尼效应后,自由表面会产生一个朝向籽晶方向的流动,该流动到籽晶附近时会发展为向下的流动(见图18(d)中A处),不利于C溶液流动到籽晶表面,会抑制C的输运进而影响SiC单晶生长。图17(c)和图18(c)对比可发现,考虑马兰戈尼效应后,籽晶下方C浓度明显降低,这也证明马兰戈尼效应对SiC单晶的生长有不利影响。

在TSSG生长SiC过程中,外部线圈会在坩埚内部形成电磁场,熔体会受到洛伦兹力的影响而导致流体运动状态发生改变。2011年,Mercier等[64]针对外部加热线圈的位置和频率对坩埚内高温溶液的影响进行了建模和数值计算。首先,他们在仅考虑电磁对流的情况下进行了模拟计算,通过只改变线圈的频率与位置来研究电磁力的影响(模拟结果见图19)。后续又在考虑浮力对流的因素下进行了仿真。发现高频率线圈产生的磁场只有在液体的外围产生较大影响,对液体内部影响几乎可以忽略不计;低频率产生的洛伦兹力较小,但分布更均匀,影响范围也较大。另外,电磁力产生的对流影响相较于浮力对流而言较小,整个流动过程还是由浮力对流主导,但电磁力对籽晶附近的对流影响较大,会使籽晶下方附近流速显著增加。

为了提高SiC晶体的生长率,Mercier等[65]又针对交变磁场对高温溶液中C的输运展开了研究,使用的模型及模拟结果如图20所示。研究通过改变线圈的位置与频率来控制溶液内洛伦兹力的分布和大小,发现C通量会受到线圈的位置与频率的显著影响,但对温度场的影响几乎可以忽略不计。通过数值计算发现将线圈置于溶液上方并且使用低频率线圈可能是最有利于SiC单晶生长的情况。

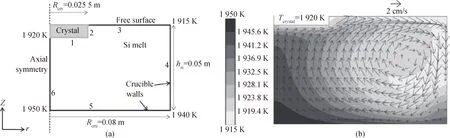
图20 Mercier生长炉模型示意图与仿真结果[65]。(a)初始条件与几何模型;(b)只考虑浮力和马兰戈尼对流情况下硅熔体中的对流与温度分布Fig.20 Schematic diagram and simulation of the Mercier growth furnace model[65].(a) Initial conditions and geometric models;(b) temperature and flow velocity results in the silicon melt for pure thermal case (buoyancy and Marangoni convection)

Ariyawong等[66]通过对TSSG法生长SiC单晶的模拟计算研究发现,在使用单个线圈进行感应加热时,当线圈频率低于某一临界值时,线圈产生的电磁对流可以控制熔体中C的运输,从而使SiC单晶生长速度显著提高。高温溶液中过弱或过强的对流均不利于快速生长高质量SiC单晶,对流太弱阻碍C运输,生长缓慢;对流太强导致SiC单晶不均匀、缺陷多、质量差。为了在这两者之间找到更适合生长的环境,Wang等[67]在考虑了籽晶旋转的情况下对垂直磁场(vertical magnetic field, VMF)和勾形磁场(cusp magnetic field, CMF)产生的影响进行了数值模拟仿真研究,希望通过调控磁场增强TSSG生长过程中的C输运,模拟发现弱的CMF可用于控制电磁对流,抑制马兰戈尼对流;将籽晶旋转与溶液内垂直磁场进行结合可以有效提高单晶生长速度和均匀性,提高晶体质量。Wang等[68]又针对线圈频率与峰值电流对熔体的影响进行了模拟计算,证明了TSSG生长SiC单晶过程中溶液流动主要是洛伦兹力导致的电磁对流与表面张力梯度导致的马兰戈尼对流的融合,而籽晶附近电磁对流可以抑制马兰戈尼对流影响。

5 对C的溶解与输运研究——传质模块

对高温溶液内C输运的研究一直是TSSG生长SiC单晶中的研究重点,TSSG法能否生长出高质量SiC单晶很大程度上取决于C是否能从坩埚壁等高C浓度处持续均匀地传递到籽晶附近。对C在溶液中的传质现象进行数值模拟可以准确获得C在坩埚内部的浓度分布、过饱和度等信息,是优化TSSG模型传质模块的有效途径。在TSSG生长SiC单晶的数值模型中,C的输运相关控制方程如式(4)所示[33]:

传质方程:

(4)

式中:C是碳的摩尔浓度;D是溶质扩散系数(D=1.7×10-8m2/s)。在模拟计算中,通常把C平衡浓度Ceq设置为坩埚-高温溶液、SiC单晶-高温溶液交界面的边界条件。Ceq的值由式(5)给出:

(5)

式中:ρSi是液态硅溶液的密度;MSi是硅的摩尔质量;xCeq是C平衡时的摩尔分数,其值随温度变化的关系式[69]如下:

(6)

有些模型为了描述坩埚内C溶解或析出的趋势,定义了一个过饱和度S:S>0时,C将会析出;S<0时,C会继续溶解。

S=C-Ceq

(7)

数值模拟模型中SiC单晶的生长速率Vg是根据籽晶表面处的C通量计算出来的,其表达式如式(8)所示。其中MSiC是碳化硅的摩尔质量,ρSiC是碳化硅密度,n为垂直于籽晶面的单位向量。

(8)

有了以上几个方程便可以利用数值模拟TSSG生长SiC单晶中溶质C的行为。图21是Lefebure等[49]使用的计算模型,以及将C平衡浓度Ceq设置为坩埚-溶液、SiC籽晶-溶液界面的边界条件时计算出的溶质C的浓度分布图。

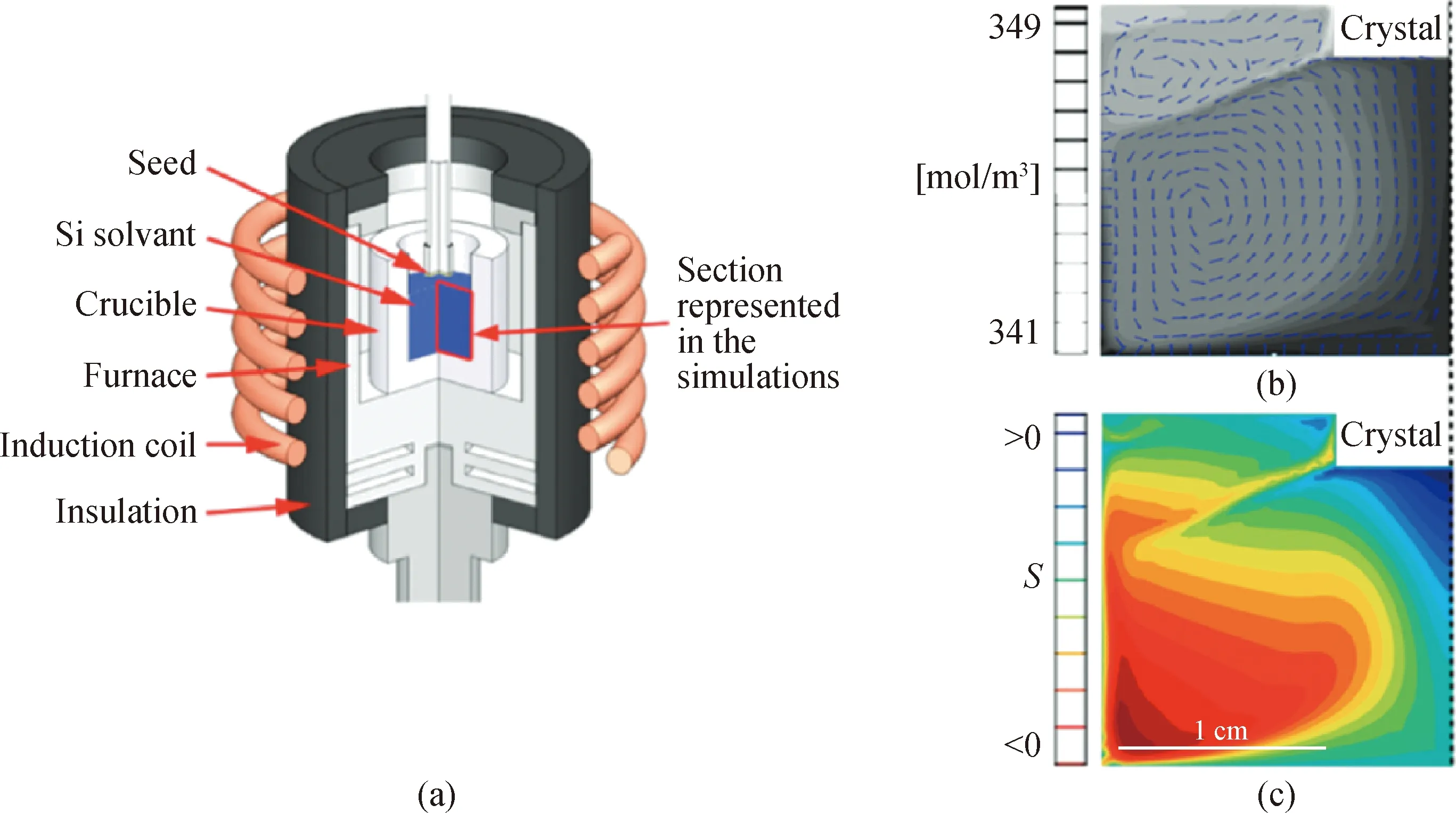
图21 Lefebure的计算模型与仿真结果[49]。(a)TSSG坩埚的示意图;(b)C浓度的分布(箭头表示归一化C通量);(c)C过度饱和度分布(S的计算表达式见式(7))Fig.21 Lefebure’s model and simulation results[49].(a) Schematic diagram of TSSG furnace; (b) carbon concentration (arrows indicate the normalized carbon flux); (c) the distribution of supersaturation in the liquid (S is calculated from Eq.(7))

在实验中作者发现对流在C从溶解区到结晶区的输运中起到了重要作用。指出了SiC晶体生长的限制参数是C的溶解度而不是C的输运,指出了提高增长率需要使用助溶剂增加C的溶解性的观点,如使用Ti-Si 或Cr-Si溶液体系。除此之外,Yoon等[57]针对C从石墨坩埚的溶解进行了研究。作者认为形成于Si溶液与石墨坩埚的接触面的SiC层也可当作C源。并用实验指出了含有SiC涂层的石墨坩埚可以有效提高溶液中C浓度,提高TSSG法制备 SiC单晶的增长率,尤其是在晶体生长初期和低温条件下效果更佳。该结论不同于大多数假定C直接来源于石墨坩埚的研究,为优化坩埚内C浓度提供了新思路。

如上所述,将C尽可能多地溶解到高温溶液中是TSSG法生长SiC单晶的重点。但C在纯硅溶液中的溶解度很低(1 700 ℃硅溶液中C溶解度仅有0.06%)[71],虽然温度的升高会一定程度上提高溶解度,但C的溶解度依然是制约SiC单晶生长的重要因素。在溶液中加入助溶剂元素是增加高温溶液对 C 的溶解度的有效途径。如向高温溶液中掺杂Ti或Cr可以有效提高C的溶解度[70,72-73]。但在增加溶解度的同时,助溶剂元素也会改变高温溶液的密度、黏度、表面张力、凝固点等与晶体生长密切相关的物理参数,从而直接影响晶体生长的热力学和动力学过程[11]。在数值模拟领域,选用不同的助溶剂体现在数值模拟过程中的操作主要是通过改变模型中高温溶液热力学与流体力学参数,如密度、黏度、表面张力和C在溶液中的扩散系数等。不同助溶剂对应不同参数会得到不同计算结果,一般而言模拟软件很少提供这些混合材料的数据,这些参数具体值还需要通过实验或其他计算获取。

6 新的进展——与人工智能技术的结合

研究者们在传统数值模拟基础上进行了很多新的尝试。例如将数值计算模拟与当前迅猛发展的机器学习(machine learning, ML)、人工神经网络(artificial neural network, ANN)等现代人工智能技术相结合,优化TSSG法生长SiC单晶的计算模型和预测模拟结果。机器学习是人工智能科学的分支,是一种通过数据或以往的经验来自动改进计算机算法的研究[74],它可以让计算机更有效地处理数据。研究者们利用机器学习,通过大量的数据对所用模型进行训练,分析出数据中隐藏的结构或规律,可对事件的发生进行判断或预测[75]。机器学习主要分为三类,有监督学习、无监督学习和强化学习,图22给出了它们的主要工作流程[76-77]。

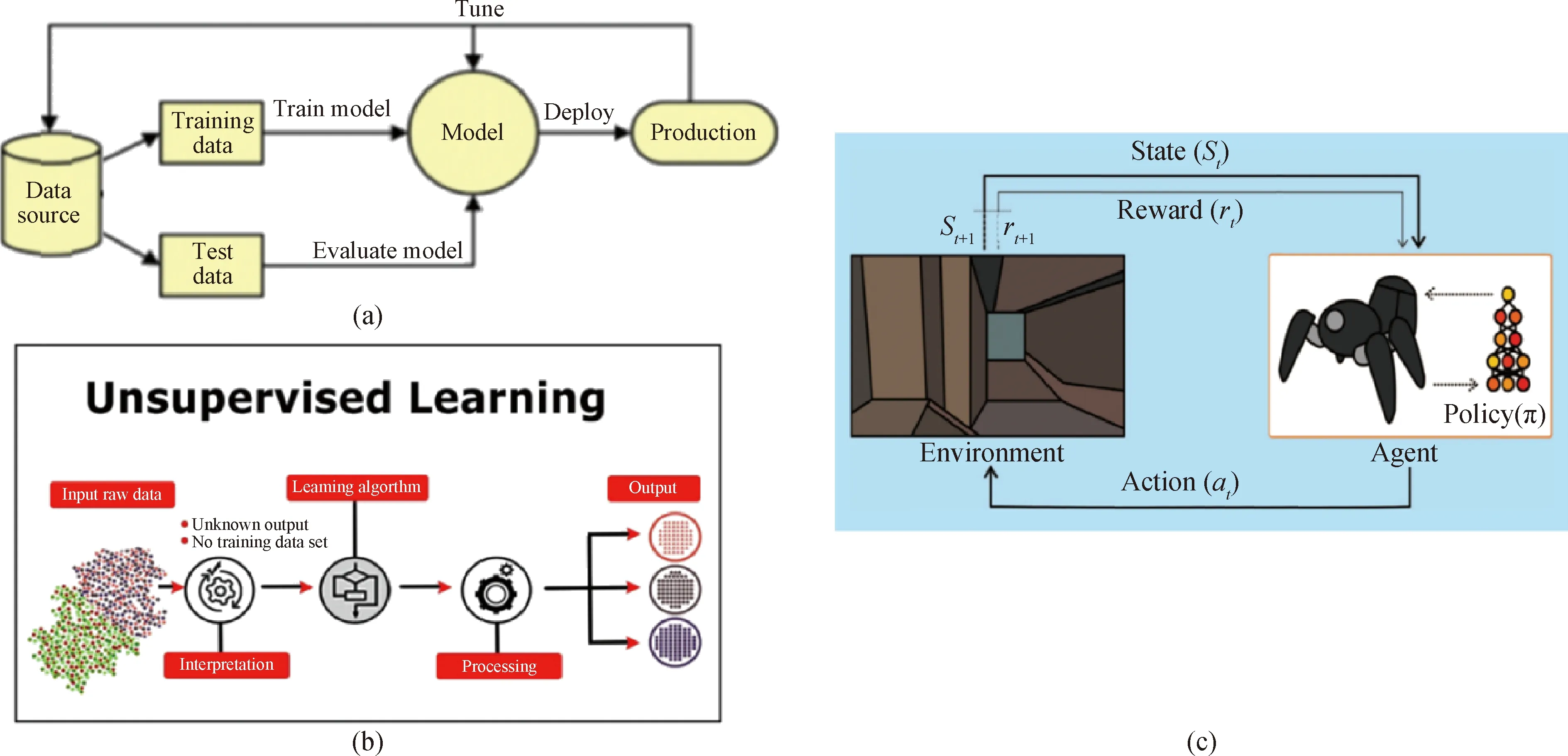
图22 机器学习的工作流程图。(a)有监督学习[76];(b)无监督学习[76];(c)强化学习[77]Fig.22 Working flow chart.(a) Supervised learning[76]; (b) unsupervised learning[76]; (c) reinforcement learning[77]

在晶体生长的数值模拟领域,机器学习技术主要运用在预测晶体生长模型的仿真结果及模型参数优化上[78]。2018年,Tsunooka等[79]运用了上述有监督机器学习模型,如图22(a)所示,对TSSG法生长SiC单晶的CFD模拟进行了预测。他们建立了TSSG生长SiC单晶的计算模型并定义了其主要参数如温度分布、籽晶尺寸、籽晶和坩埚的旋转速率等,模型与参数取值区间如图23(a)～(c)所示。通过使用不同的可变参数值对模型进行800次CFD模拟,以计算不同温度和晶种旋转配置下的过饱和度分布和流速。然后使用这些结果数据来训练预测模型,再用训练好的模型反过来对模型进行CFD预测。结果此模型进行预测所花费的时间要远小于传统数值模拟计算需要的时间(比传统CFD模拟快约107倍),而且其预测结果与实际计算仿真所得结果高度吻合,如图23(d)、(e)所示。这种方法所带来的巨大时间优势有望显著加快研究者对晶体生长模型的开发。

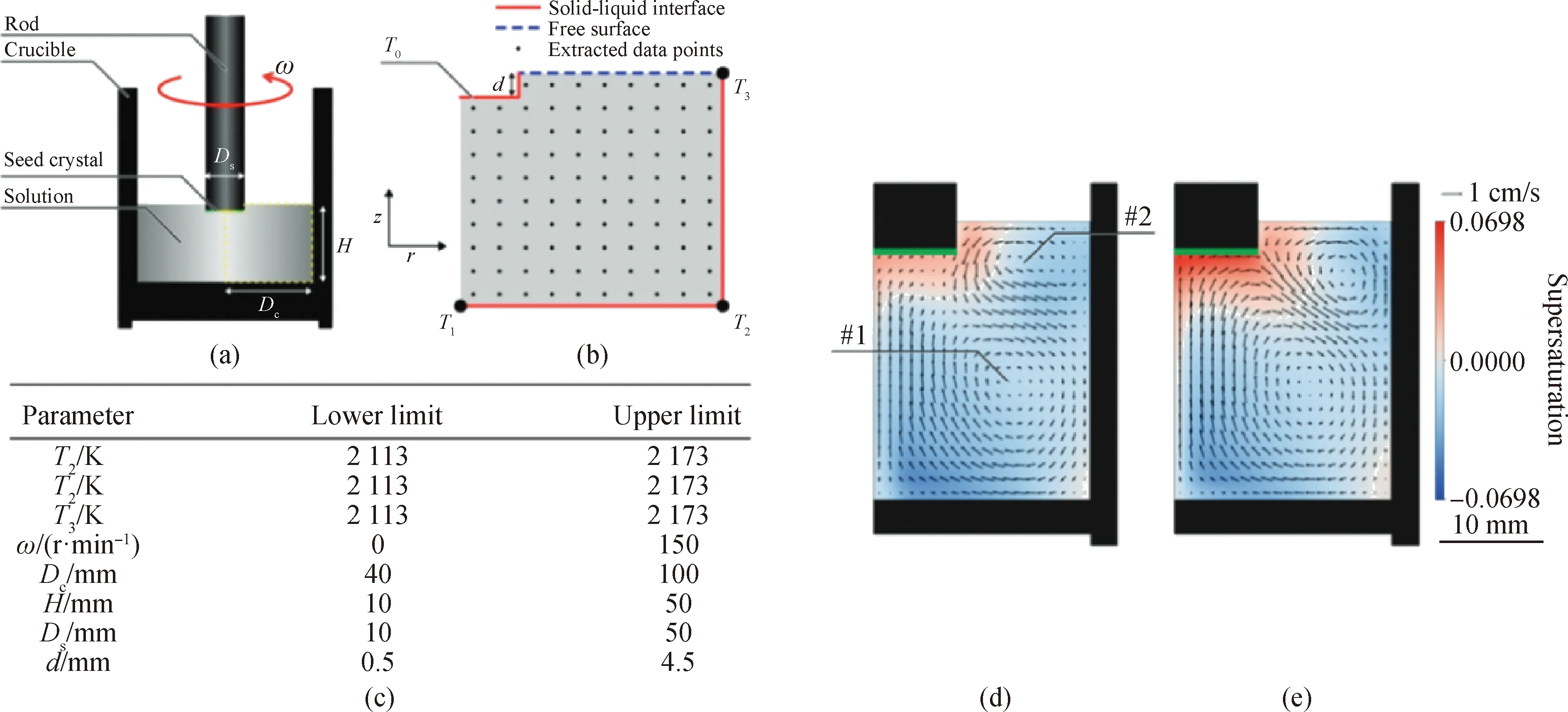
图23 Tsunooka的机器学习预测实验[79]。(a)TSSG法生长SiC单晶模型示意图;(b)CFD的计算域;(c)参数区间;(d)机器学习模型预测的结果;(e)CFD仿真结果Fig.23 Tsunooka’s prediction experiment by ML[79]. (a) Configuration of the TSSG process; (b) computational domains for CFD simulations; (c) ranges of variable parameters;(d) results of ML model prediction; (e) CFD simulation results

2020年,Sekimoto等[38]利用强化学习与数值模拟相结合来探索SiC单晶生长的最优控制方案。在研究中,他们利用RL模型控制电磁场,削弱马兰戈尼对流的影响;采用TSSG法生长的二维数值模拟结果对RL模型进行训练,发现在RL模型控制下,晶体生长速率可以得到显著提升;将RL优化过的感应线圈参数用于三维数值模拟,结果也表现出了更高更均匀的生长速率。晶体生长是一个动态的过程,在此过程中施加动态的调控来保证生长界面所处的状态持续稳定对于晶体质量有重要的意义,尤其是长时间晶体生长的情况[11]。2021年,Dang等[80]通过训练机器学习模型,即时预测生长炉内非稳态变化,如坩埚损耗等情况,并进行及时调整。设计出能够保证生长条件始终如一的自适应控制模型,可保持高速、均匀、长时间的生长速率。Takehara等[81]也对机器学习预测TSSG生长SiC单晶方面进行了研究。他们发现静磁场和籽晶旋转速率对晶体生长和溶液流动的影响较大,利用贝叶斯算法对静磁场和籽晶旋转速率等相关控制参数进行了有效优化,并对贝叶斯优化确定的最优配置进行了详细的分析等。这些研究无疑证实了传统数值计算与新兴人工智能技术相结合的潜力与独特优势,相关研究将会有力地推动数值模拟晶体生长领域的发展。

7 结语与展望

TSSG法生长SiC单晶具有生长温度低、易扩径等多种优势,近20年来获得了很多研究者的关注。但TSSG法生长机理复杂,影响因素较多,在实际生长过程中难以对生长条件进一步改进与优化,而利用数值计算方法来模拟晶体生长过程可有效解决这一问题。本文首先介绍了数值模拟TSSG法生长SiC单晶研究的发展历程和原理,然后系统地描述了数值模拟模型使用的传热、流动和传质模块,以及生长过程中起主要作用的几种影响因素,如马兰戈尼力、电磁力、旋转带来的剪切应力等,梳理了迄今为止人们对生长模型的一些改进和新方法(如CFD与机器学习的结合等)。基于以上发展历程,本文认为未来对数值模拟TSSG法生长SiC单晶的研究需要重点关注以下几个方面:

1)提高C在高温溶液中的溶解度,设计高C溶解度的TSSG生长单晶碳化硅模型。制约TSSG法生长SiC单晶速度的重要因素之一是C在高温溶液里溶解度过低,无法保证溶液中有充足的C元素在籽晶处析出。未来可重点关注于提高C在高温溶液中溶解度的相关数值模拟研究,可通过研究生长过程中C的溶解行为,设计不同热场、流场、坩埚结构等,获得更高C溶解度的TSSG生长模型。

2)利用数值模拟手段进一步探究C在高温溶液中输运行为。目前进行的数值模拟工作通常简单地将石墨坩埚壁作为C源、溶液中C的平衡浓度作为边界条件来计算C的浓度分布。对C在溶液中具体运动、C源的变化(如生长中产生的SiC沉淀也可作为C源)、生长中坩埚损耗等影响C输运行为的因素研究还不够深入。对C在高温溶液中输运行为进行深入研究对提高单晶生长的速度和质量是十分重要的。

3)利用机器学习加速数值模拟的计算速度,设计更准确、高效、适用于优化SiC单晶生长的机器学习模型也是未来研究工作的重点之一。加强晶体生长的数值模拟计算与机器学习的融合,如构建更精确的训练模型,考虑更多优化参数,选择更适宜的参数范围等。充分利用机器学习的快速计算与预测能力来降低数值模拟计算时间和计算成本,从而促进对TSSG法生长SiC单晶模型的设计与实验工艺的优化。

最后,虽然TSSG法的数值模拟工作距离完美还原实际生长过程中炉内的各种现象还存在一定的差距,但对晶体生长过程中主要因素及影响的定性或定量的分析都已得出了很多有价值的结论,指导优化了TSSG法生长SiC单晶的实验。相信通过研究者们对数值模拟、机器学习、TSSG法单晶生长等进一步探索,TSSG法制备SiC单晶一定会在未来充分发挥其优势,实现产业化,进而推动整个SiC产业的发展。