一体化光幕阵列测量误差分析与结构参数优化
于国栋 ,王春阳 ,冯江海 ,张月 ,刘晓辰 ,李忠琦 ,程志远
(1 中国人民解放军 63869部队, 白城 137001)
(2 中国科学院西安光学精密机械研究所 光电跟踪与测量研究室, 西安 710119)
0 引言
随着身管武器的发展,速射武器得到越来越广泛的应用,为了对该类武器性能进行评价,需实现高射频的连发测量,测量设备一般采取非接触式测量原理实现[1-2]。常见的测量原理主要包括:声学原理[3]、图像原理[4]及光幕阵列原理[5]等。声学原理基于激波传感器构成测量阵列,它仅能测量超音速弹丸且相近的连发弹丸容易相互干扰[6];图像原理多采用CCD交会的方式构成探测幕面,对穿过的弹丸进行拍摄后解算弹丸坐标[7],如需测量弹丸飞行速度则需要两个及以上的探测幕面,且成本较高;光幕阵列原理多采用光敏传感器接收人工光源或天空背景光形成探测幕面[8],多个探测幕面按照指定形式排列成光幕阵列,通过光幕阵列结构参数和弹丸到达各光幕的时间解算弹丸飞行速度,该原理由于响应时间短、测速范围广及成本低廉等优点,已在靶场测试领域得到广泛应用。
为了提高光幕阵列测量的精度,国内外学者根据光幕阵列测量原理,主要将影响精度的因素分为光幕阵列测量模型、弹丸过幕时刻测量精度以及光幕空间结构失真三类。不同形式的光幕阵列测量参数不同[9-10],以六光幕阵列测量模型为例主要包括双N形、双V形以及双平行形阵列等,不同测量模型对各类弹丸飞行参数的测量精度均有所差异,这是由于不同模型下各飞行参数的解算原理决定的[11-12];弹丸过幕时刻测量精度在当前电子技术发展的水平下,主要受到过幕时刻提取算法的影响,如光幕空间形状产生变形情况下各光幕时刻提取一致性的补偿[13];光幕空间结构失真包含光幕空间结构被准确获取和光幕空间结构在测量现场的复现,前者一般在光幕阵列测量设备设计和生产后,在实验室进行精确标定获取[14],而后者则考虑靶场比较恶劣条件对光幕测量设备中光幕结构形变的影响[15]。目前越来越多的研究将分体式光幕阵列测量模型转换为一体化测量模型[16],这样既可减少测量模型中的参数,也便于现场使用。针对一体化光幕阵列测量模型中各结构参数对弹丸飞行参数测量误差影响的分析,不但有利于身管武器性能测试中的精度评估,也可为一体化光幕阵列的工程设计和结构优化提供技术依据。
1 一体化光幕阵列测量模型及参数
光幕阵列法测量的基本原理是在外弹道上截取数米左右的区间(区截弹道),并在区截弹道内按照规定形式布置若干个光幕构成光幕阵列,通过压缩弹丸穿过各光幕的信号提取弹丸到达各光幕面的时间,再结合已知的光幕空间结构参数(简称结构参数),解算弹丸的飞行参数。
以传统的双N型六光幕阵列天幕立靶为例,分为前靶和后靶,即通过固定在靶体上的镜头、光阑及传感器等,由两个分立的靶体分别形成两个单N形光幕阵列。这样以来前靶和后靶之间的距离可以根据测量需求随意设置,但是每次测量前都需要经过布靶,即需要将前靶和后靶摆放在指定位置后对它们进行对调平、对正校准,并测量靶距、高低差等作为测量模型中的参数。因此,分体式光幕阵列天幕立靶的缺点在于它不但增加了布靶工作量,还给测量模型中引入了更多的可变参数,若这些参数在测量现场难以精确获取,则可能带来较大的测量误差。
将前靶和后靶固定在一个底座上并预先完成对准及高低差矫正等工作,这样在现场测量时仅需将其布放后调平,不仅便于使用且对测量模型中的部分参数实现了固化,保障了设备的稳定性和精度。一体化光幕阵列测量模型如图1。

图1 一体化六光幕阵列测量模型Fig.1 The integrated six light screen array measurement model
一体化光幕阵列测量模型中,前靶和后靶经调校后固定在底座上与底座相对关系保持不变,经调校使得两者仅沿弹道方向分开一定距离且相互平行,分开的距离记为靶距s。在靶体上方空间形成呈双N形排列的六个光幕,依次记做G1、G2、G3、G4、G5、G6,光幕之间的角度固定称为光幕夹角。取水平弹道方向为X轴方向,竖直向上为Y轴方向建立直角坐标系,光幕面在坐标系内的投影如图2。

图2 双N形六光幕投影Fig.2 The double N-shaped six light screen projection
图2(a)为光幕面在XOY面内的投影,其中α为光幕面竖直角度,图2(b)为光幕面在XOZ面内的投影,其中β为光幕面水平角度,统称为光幕角度参数。
飞行的弹丸依次穿过六个光幕得到一组过幕信号,对过幕信号进行压缩后可提取得到一组时刻序列t1~t6,表示弹丸到达各光幕的时刻。利用时刻序列与 6个待测参数[x,y,z,vx,vy,vz](分别表示沿三个轴向的速度和在光幕内的空间坐标)建立时空对应关系,匀速弹道模型下弹丸时空关系可表示为
式中,ti表示弹丸到达光幕i的时刻。将其带入光幕结构参数表示的各光幕空间位置,测得的弹丸飞行参数为
式中,
一体化测量模型公式中,调校可使得高度差h为零,测量模型更为简化。
2 待优化参数及误差传播公式
光幕阵列用于弹丸飞行参数测量,获取的测量结果[x,y,z,vx,vy,vz]中主要被测参数包括:弹丸空间横坐标z和纵坐标y,以及弹丸沿三个轴向的飞行速度矢量和v,对应式(2)中[vx,vy,vz]速度沿坐标轴方向分量的矢量和。这些参数的测量结果可简化为
式中,t(ii=1,2,3,…,6)表示弹丸到达六个光幕的时间序列。
经分析可知,测量模型中的过程参数主要包括:光幕空间角度参数α和β、靶距s、高度差h以及过幕时间序列ti。由于这些参数均参与了弹丸飞行参数的解算,因此它们直接影响测量结果的精度,理论上对它们的取值进行优化对一体化光幕设计具有重要作用。其中过幕时间序列ti的获取由光幕阵列中的光电传感器特性及过幕信号提取算法决定,与一体化测量模型设计参数无关,因此主要讨论光幕空间角度参数α和β、靶距s、高度差h。
根据测量模型和误差理论,在光幕测量模型下其他测量参数不变的条件下,仅考虑光幕角度参数α和β引起的测量偏差,推导误差传播公式,结果分别为
同理,根据测量模型和误差理论,在光幕测量模型下其他测量参数不变的条件下,仅考虑靶距s和高度差h引起的测量偏差,推导误差传播公式,结果分别为
基于上述误差传播公式理论基础,分别针对不同设计参数影响下的一体化光幕阵列测量模型误差进行分析,获取不同设计参数对光幕阵列测量误差的影响规律。
3 仿真分析
根据理论分析结果在MATLAB中进行仿真分析,一方面建立一体化光幕阵列测量模型,模型中的待优化参数取值覆盖设计中可能取值的变化区间。另一方面,除了待优化参数外对一体化光幕阵列测量模型测量误差的影响因素还包括弹丸穿过光幕的时刻序列的获取精度以及弹丸自身的飞行参数特性。其中弹丸过幕时刻序列的获取精度由光幕阵列中的光电传感器特性及过幕信号提取算法决定,弹丸自身飞行参数特性则包括弹丸的着靶位置、飞行速度等相关参数。
为了使仿真分析结果更贴近当前一体化光幕阵列测量的真实结果,参考光幕阵列测试技术水平的发展现状,对仿真中的各项必需参数设计如下:一体化双N型光幕阵列测量模型中,一般认为第一个光幕G1为起始光幕面,即认为时刻t1=0,其余时刻相对于t1获取,取所有幕面时间获取误差均为δt=0.5 μs;结构参数角度可采用双经纬仪空间标定技术标定光幕夹角[14],取光幕角度设计典型值α=β=25°,实际光幕角度加工误差δα=δβ=0.01°;靶距典型值s=2 m,实际靶距加工误差δs=2 mm;前后靶高度差设计典型值h=0 mm,实际高度差加工误差δs=2 mm。取图1所示坐标YOZ平面内对称分布的1 000 mm×1 000 mm矩形为靶面。弹丸飞行参数特性中,弹丸的预设弹道线位于靶体上方1 m位置穿过靶面中心,取弹丸速度与预设弹道线方向一致,弹丸速度v=720 m/s。
3.1 光幕角度参数优化
考虑光幕面竖直角度α,使其在可能的设计范围10°≤α≤80°内连续变化,其余仿真条件不变,分别得到一体化光幕阵列测量模型下弹丸横坐标、纵坐标及速度矢量和的测量误差仿真结果,如图3。

图3 光幕面竖直角度α影响下的测量误差Fig. 3 Measurement error under the influence of horizontal angle α
由图3可知,在光幕面竖直角度α的取值从10°逐渐增大至80°的过程中:弹丸横坐标测量误差恒为0.95 mm,该值由竖直角度α以外的其他因素引起,α的取值对弹丸横坐标测量误差不产生影响;弹丸纵坐标测量误差呈递减趋势,由初始最大值1.45 mm逐渐减小至0.05 mm,α的取值的增大有助于减小靶面中心纵坐标测量误差,且在α由10°增加至20°的过程中误差减小趋势显著,在α由20°增加至80°的过程中误差减小趋势逐渐减弱;弹丸速度测量误差恒为377.09 mm/s,该值由竖直角度α以外的其他因素引起,α的取值对弹丸速度测量误差不产生影响。
考虑光幕面水平角度β,使其在可能的设计范围10°≤β≤80°内连续变化,其余仿真条件不变,分别得到一体化光幕阵列测量模型下弹丸横坐标、纵坐标及速度矢量和的测量误差仿真结果,如图4。

图4 光幕面水平角度β影响下的测量误差Fig. 4 Measurement error under the influence of vertical angle β
由图4可知,在光幕面水平角度β的取值从10°逐渐增大至80°的过程中:弹丸横坐标测量误差呈递减趋势,由初始最大值2.50 mm逐渐减小至0.08 mm,β的取值的增大有助于减小靶面中心横坐标测量误差,且在β由10°增加至20°的过程中误差减小趋势显著,在β由20°增加至80°的过程中误差减小趋势逐渐减弱;弹丸纵坐标测量误差恒为0.55 mm,该值由水平角度β以外的其他因素引起,β的取值对弹丸纵坐标测量误差不产生影响;弹丸速度测量误差恒为377.09 mm/s,该值由水平角度β以外的其他因素引起,β的取值对弹丸速度测量误差不产生影响。
对仿真结果进行分析,无论是光幕竖直角度还是光幕水平角度,均符合取值越大越有利于降低测量误差,但仍需关注的是光幕面角度取值过大将直接减小光幕在空间覆盖的范围,即缩小有效探测区域,因此一体化光幕设计中应对测量误差和探测范围等因素综合考虑。根据图3和图4的仿真分析结果,光幕角度从10°增至20°过程中测量误差减小趋势非常明显,在20°增至30°过程中减小趋势逐渐减弱,在30°之后减小的误差绝对量则较为有限,因此光幕竖直角度α和水平角度β在设计中取值范围选取20°~30°较为合适。
3.2 靶距参数优化
考虑前靶和后靶沿预设弹道方向的布放距离s,其取值直接影响一体化光幕阵列的测量精度和外形长度,在其与仿真条件不变的情况下,取靶距s由100 mm逐渐增大至3 000 mm进行仿真,得到一体化光幕阵列测量模型下弹丸横坐标、纵坐标及速度矢量和的测量误差仿真结果,如图5。

图5 靶距s影响下的测量误差Fig.5 Measurement error under the influence of target distance s
由图5可知,在靶距s从100 mm逐渐增大至5 000 mm的过程中:弹丸横坐标测量误差呈递减趋势,由初始最大值3.26 mm逐渐减小至0.95 mm,s的取值的增大有助于减小靶面中心横坐标测量误差,且在s由100 mm增加至1 500 mm的过程中误差减小趋势显著,在s由1 500 mm增加至5 000 mm的过程中误差减小趋势逐渐减弱;弹丸纵坐标测量误差呈递减趋势,由初始最大值10.50 mm逐渐减小至0.74 mm,s的取值的增大有助于减小靶面中心纵坐标测量误差,且在s由100 mm增加至1 500 mm的过程中误差减小趋势显著,在s由1 500 mm增加至5 000 mm的过程中误差减小趋势逐渐减弱;弹丸速度测量误差呈递减趋势,在s由100 mm增加至1 000 mm的过程中误差减小趋势极为显著,当s增至1 000 mm时速度测量误差已由初始误差极大值7 541.81 mm/s减小至754.18 mm/s;在s由1 000 mm增至3 000 mm的过程中,速度测量误差由754.18 mm/s减小至251.39 mm/s;曲线末段s由3 000 mm增至5 000 mm的过程中速度测量误差仅从251.39 mm/s减小至150.84 mm/s,即靶距s的增大对速度减小速度测量误差的作用逐渐减弱。
对仿真结果进行分析,靶距s的增大对弹丸横、纵坐标及速度的测量误差影响规律基本一致,增大靶距s有利于减小弹丸飞行参数测量误差,但过大的靶距会使光幕阵列外形过长,不利于现场使用和布放,也需使用较长的线缆对前靶和后靶进行连接,因此一体化光幕设计中应对上述因素综合考虑。根据图5所示仿真结果选择靶距s为1 500 mm至2 500 mm较为合适。若因某些场合特殊需求需提高弹丸飞行参数测量精度,仍可考虑继续增大靶距s以减小弹丸横、纵坐标尤其是飞行速度的测量误差。
3.3 高度差参数优化
考虑前靶与后靶沿水平高度布放差距h,当前靶高于后靶时h为正值,当前靶低于后靶时h为负值。选取其在合理的设计范围-200 mm≤h≤200 mm内连续变化,其余仿真条件不变,分别得到一体化光幕阵列测量模型下弹丸横坐标、纵坐标及速度矢量和仿真结果,如图6。

图6 高度差h影响下的测量误差Fig.6 Measurement error under the influence of height difference h
由图6可知,在高度差h的取值从-200 mm逐渐增至200 mm的过程中:弹丸横坐标测量误差恒为1.00 mm,该值由高度差h以外的其他因素引起,h的取值对弹丸横坐标测量误差不产生影响;弹丸纵坐标测量误差恒为1.24 mm,该值由高度差h以外的其他因素引起,h的取值对弹丸纵坐标测量误差不产生影响;弹丸速度测量误差呈先减少后增大趋势,且在h=0 mm附近达到最小值728.66 mm/s。
对仿真结果进行分析,一体化光幕阵列设计中取前靶与后靶高度差h=0 mm有助于减小弹丸飞行速度测量误差。
3.4 靶面测量误差分布
根据一体化光幕阵列各项参数的仿真分析结果,优化设计的测量模型参数选取:光幕竖直角度α和水平角度β均为25°,前靶与后靶靶距s为2 000 mm,高度差h=0 mm,并考虑所有幕面时间获取误差均为δt=0.5 μs,实际光幕角度加工误差δα=δβ=0.01°,实际靶距加工误差δs=2 mm。根据图1所示测量坐标系,在光幕交汇点左右方向选取横坐标为[-500 mm,500 mm],在光幕交汇点镜头上方选取纵坐标为[ 800 mm,1 800 mm],形成1 000 mm×1 000 mm的矩形靶面,对弹丸飞行横坐标、纵坐标及弹丸飞行速度进行综合误差仿真分析,结果如图7。

图7 靶面内测量误差分布Fig.7 Measurement error distribution in target plane
由图7可知,在优化的一体化光幕阵列结构参数测量模型下,选定的矩形靶面内弹丸飞行横坐标测量误差在靶面下方中心区域时最小,主要随横坐标绝对值的增大沿靶面横坐标方向向两侧呈增大趋势,并随纵坐标的增大而增大,横坐标测量误差不超过1.50 mm。弹丸飞行纵坐标测量误差在靶面下方区域时最小,主要随纵坐标的增大而增大,且纵坐标测量误差不超过2.10 mm。弹丸飞行速度在矩形靶面内基本呈均匀分布,测量误差为728.70 mm/s。
4 实弹试验及数据
针对一体化六光幕阵列进行实弹射击试验,将双N形六光幕阵列天幕立靶固定在底座之上并调整前靶和后靶状态使其相互平行,通过激光测距仪确定调整后的前靶与后靶靶距s=2 m,h=0 m。双N形六光幕阵列光幕空间角度设计值参考仿真优化结果取25°,由于存在机械加工误差,在试验前通过平面拟合的方法对光幕角度精确标定,结果为α=24.94°,β=24.61°。
在一体化光幕阵列后放置一个纸板靶,对比光幕阵列测量坐标和纸板靶上弹孔坐标之间的偏差,实现弹丸坐标测量误差比对。在预设弹道上与一体化光幕阵列一起放置一套激光测速靶专门用于弹丸飞行速度测量,实现弹丸飞行速度测量误差比对。对1 m×1 m矩形靶面进行10次射击,得到的实弹试验坐标测量和速度测量数据分别如表1和表2。

表1 实弹试验坐标测量数据Table 1 Coordinate measurement data of live fire test
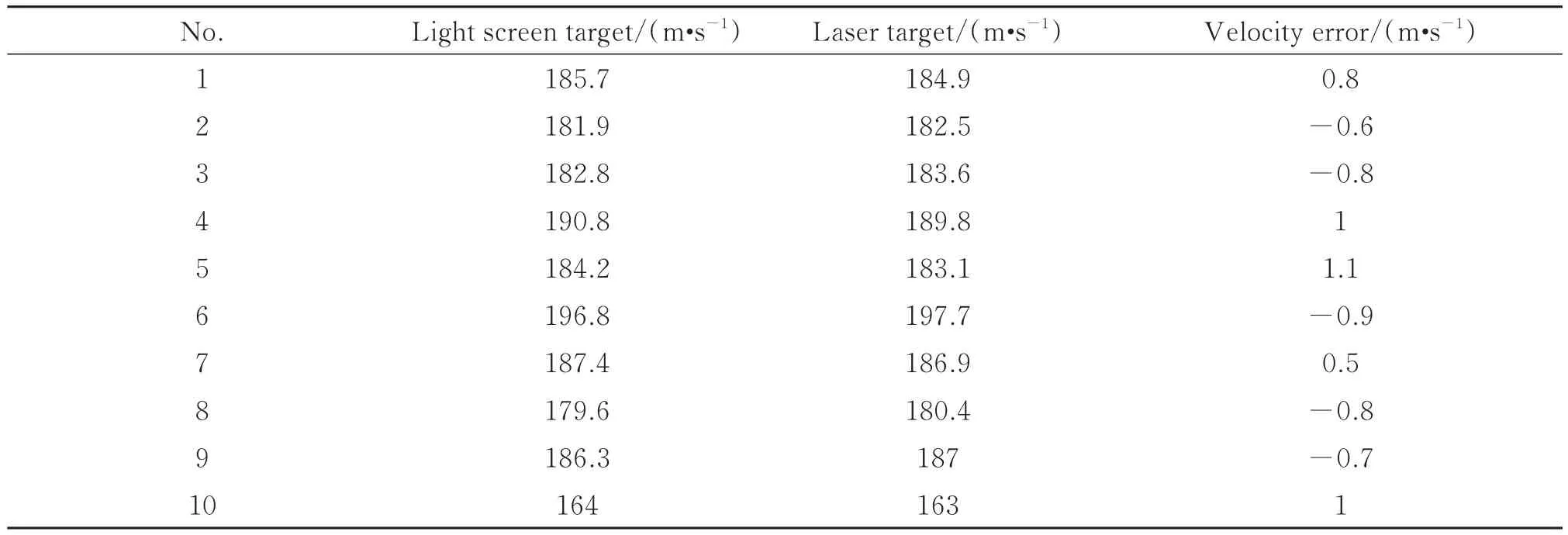
表2 实弹试验速度测量数据Table 2 Velocity measurement data of live fire test
由于实弹试验在室外进行,还引入了环境因素等的影响,因此得到的测量误差略大于仿真结果。根据表1和表2所示的试验数据,弹丸横坐标测量误差不超过3.1 mm,纵坐标测量误差不超过4.8 mm,速度测量误差不超过1.1 m/s,且误差在靶面内的整体分布与仿真基本一致。
5 结论
针对六光幕阵列测量模型参数复杂、现场布放繁琐、误差因素较多的问题,研究一体化光幕阵列测量模型,精简测量模型参数数量,提取一体化光幕阵列测量模型中结构相关的设计参数,分析其对弹丸飞行参数的影响机理,通过仿真得到各参数影响下的弹丸飞行参数测量误差影响规律,主要包括: 1) 幕面竖直角度α主要影响弹丸纵坐标测量误差,随α的增大弹丸飞行纵坐标测量误差减小且减小趋势逐渐减弱;幕面水平角度β主要影响弹丸横坐标测量误差,随β的增大弹丸飞行横坐标测量误差减小且减小趋势逐渐减弱,两者影响规律类似,由于光幕空间结构中角度增大将减小有效靶面探测区域,选择优化后的光幕竖直角度α和水平角度β为20°~30°较为合适。2) 前靶与后靶距离s对弹丸横、纵坐标及速度的测量误差均有影响,随s的增大弹丸飞行参数测量误差逐渐减小且减小趋势逐渐减弱,由于过大的靶距不利于运输、现场布放和使用,选择优化后的靶距s为1.5~2.5 m较为合适;前靶与后靶高度差h主要影响弹丸速度测量误差,速度测量误差呈先减少后增大趋势,选择优化后的高度差h=0 mm较为合适。3)根据各参数影响下的弹丸飞行参数误差分布规律,为一体化光幕阵列测量模型中各参数赋予典型值并仿真分析1 000 mm×1 000 mm靶面内的误差分布,结果显示弹丸横坐标测量误差不大于1.50 mm,纵坐标测量误差不大于2.10 mm,速度测量误差不大于728.70 mm/s。4) 针对分析结果进行实弹试验,由于外场环境因素的影响,试验得到的测量误差略大于仿真结果,弹丸横坐标测量误差不超过3.1 mm,纵坐标测量误差不超过4.8 mm,速度测量误差不超过1.1 m/s。研究结果可为六光幕阵列测量设备的工程设计提供理论依据,也可为提高身管武器弹丸飞行参数测量精度提供参考。

