非平衡数据集下的高职学生就业预测模型*
熊露露 年 梅 张 俊
(1.新疆师范大学 乌鲁木齐 830054)
(2.新疆铁道职业技术学院 乌鲁木齐 830000)
(3.中国科学院新疆理化技术研究所 乌鲁木齐 830011)
1 引言
高职学生的就业率是高职院校学生培养质量的重要体现,而就业预测指对未毕业的学生能否就业进行预测,提前对可能就业困难的学生进行有效的指导,提高学生的就业率,促进高职院校学生扩招工作良性循环发展。
2 就业预测相关研究
近年来,国内外很多学者对影响学生就业的因素和就业预测模型进行了研究。李琦[1]运用互信息和权重相结合的特征选择算法HMIGW 以及XGBoost 分类预测算法,对本科毕业生就业情况和就业类型进行预测;马茂源[2]利用半监督自训练方法解决就业预测样本不均衡使分类器精度低的问题;李想[3]采用灰色模型和神经网络对大学生就业数进行预测;程昌品[4]等利用决策树算法对本科毕业生就业进行了预测。从以上文献可知,现有的就业预测研究主要面向本科生进行,高职学生就业预测的研究成果较少;此外现有的就业预测模型大多基于平衡数据集的机器学习算法,对于类别样本不平衡的数据集,分类器倾向于将所有的样本预测为样本数目较多的类别[5~6],预测结果没有实际意义。而就业预测的目的是找出数目较少的未就业学生,并基于其存在的问题进行针对性的就业指导,从而提高学生整体的就业率。以上研究成果均无法解决上述问题。围绕如何解决非平衡数据集下的高职学生就业预测问题,本文的主要贡献如下:
1)创新性地提出了基于ADASYN-SMOTE 算法的小类样本生成策略,有效地解决了机器学习对于不平衡数据集中小类样本误判问题。
2)基于ADASYN-SMOTE 算法构建后的平衡数据集,运用随机森林算法建立高职学生就业预测模型,该模型不仅具有更高的泛化能力,并且能全面准确地预测出不能就业的学生,对于提高高职学生就业率具有较高的实用价值。
3 构建高职学生就业预测模型
3.1 数据准备
3.1.1 数据对象的采集
本研究以某高职院校的毕业生就业和成绩数据为研究对象。从学校招生就业系统中提取2016年~2020年毕业生就业数据3778条记录,从教务管理系统中提取相应毕业生3 年6 学期成绩数据22668条记录。
3.1.2 数据预处理
将每名学生3年6学期所有成绩按照学号进行整合,学生成绩由原来的22688条减少到3778条。
为了能够体现学生的综合学习质量,按照人才培养方案将学生的成绩整合为基础、专业基础、专业、专业核心、技能鉴定、实习、实训、职业生涯规划、论文9 个类别的成绩。各类别平均分按照式(1)计算得到:
其中Cˉmi为第m 个学生的第i 类别成绩的平均分,每个学生成绩Ci∈(基础,专业基础…论文),m∈(1,3778)。Cmij为第m 个学生的第i类别中的j科目成绩,k为i类别中科目总数。
将就业数据和处理后的成绩数据通过“学号”关联合并,用均值填充缺失数据;将定性数据改为数值型数据,如就业属性列中“就业”为0,“未就业”为1;为了消除特征数据之间的量纲影响,运用最大-最小规范化使数据取值范围为[0,1],使各指标处于同一数量级,以便进行综合对比和评价。
3.2 就业预测指标变量选取
就业预测需要准确选取预测指标变量,本文使用递归特征消除法RFE 对就业预测指标选取。递归特征消除法(Recursive Feature Elimination,RFE)属于包装法中非线性分类器中的重要方法,该方法可以选择高质量的子集[7]。将最大最小规范化的指标数据输入到以随机森林作为基模型,目标变量为RFE的特征选择模型,通过计算得到不同特征数下模型性能分数,如图1 所示(横坐标为特征数,纵坐标为模型性能分数)。
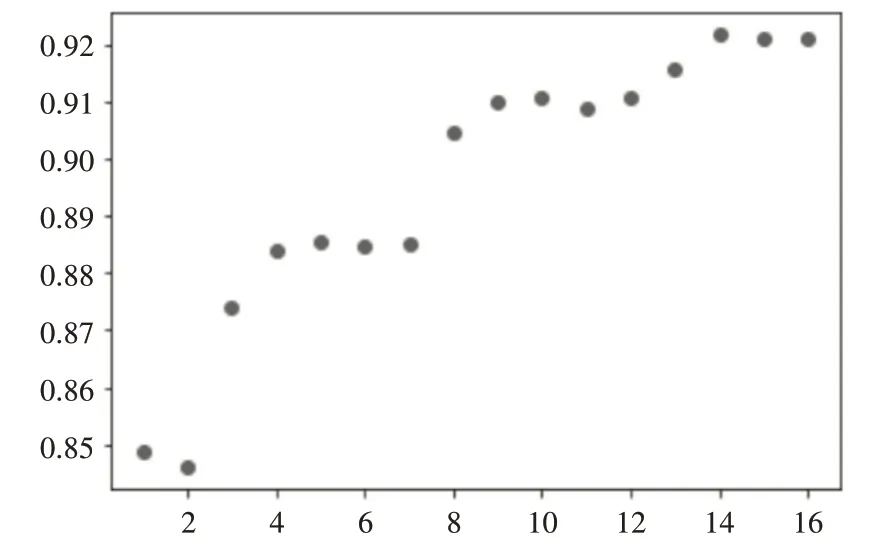
图1 特征数与模型性能之间的关系
由图1中可以看出,特征数是14时模型的性能最好,所以本研究采用排名为前14 的特征作为分类模型的特征。
3.3 基于ADASYN-SMOTE的不平衡数据处理
3.3.1 ADASYN算法
ADASYN 算法[8],根据少数类样本的分布特点自适应地引入新样本缓解数据不平衡的问题[9]。但ADASYN 算法会造成在易分类边界合成较少样本,难分类边界合成较多样本[10],易受离群点的影响。
3.3.2 SMOTE算法
SMOTE 算法[11],则是在少数类样本和其相邻少数类邻居的连线上引入合成样本,以消除类间不平衡度。但该算法未考虑样本的分布特点,合成的新少数类样本点会与原始数据高度相似,甚至重复,很难为分类器提供新的分类信息[12]。
本文数据集存在样本不均衡问题,单独使用ADASYN 算法或SMOTE 算法均无法达到平衡数据的最佳效果,故此,本文创新性地提出ADASYNSMOTE过采样算法,解决样本的均衡性问题。
3.3.3 基于ADASYN和SMOTE算法的小类样本合成算法
将整个训练集中n 个样本{xi,yi},i=1,2…n,其中xi是多维空间X 的一个样本,yi∈Y={0,1}是分类标签,yi=1是小类样本(“未就业”),yi=0是大类样本(“就业”)。ms是少类样本数,ml是大类样本数。ms+ml=n,且ms≤ml。
1)计算每个小类在样本中的K 近邻,其近邻的大样本数量记为k1;
2)比较k 与k1 的值,若k1=k,即样本点周围都是大类样本,将该小类样本删除;若k/2 ≤k1<k,则认为该样本属于边界区域中,将其放入Merge 集合中;如果0 ≤k1<k/2,则认为其不在边界区域中,将其放入Middle集合中;
3)计算Merge 和Middle 集合中样本数量,分别记为n1 和n2。其中Merge={a1,a2…an1},Middle={b1,b2…bn2};Merge集合中的插值率Gi:扩充倍数;
4)计算合成小样本的总数:G=(ml-ms)*β,其中β∈(0,1),表示加入合成样本后的不均衡度;
5)找出Merge 集合中每个少数类样本ai在n维空间的k 近邻,计算其比率,i=1,2…n1,其中Δi是ai的k 近邻中大类样本的数量,ri∈(0,1];
7)对于Merge 集合中的每个少数类样本ai根据,计算需合成的少数类样本数,按照如下的方法对ai生成gi个样本:
对1~gi个样本执行(1)~(2)循环:
(1)在每个待合成的少数类样本ai周围k个邻居中选择一个少数类样本azi。
(2)依据式(2)进行插值:
9)对于Middle 中每个少数类样本bm,其中m∈(1,n2),按照如下的方法对于每个少数类样本bm生成N个样本:
对1~N个样本执行以下循环:
(1)以欧式距离为标准计算其到少数类样本集中所有样本的距离,得到其k 个近邻,记为Z={b1,b2…bn3},从中选取bm1,其中m1∈(1,n3)。
(2)按照式(3)计算插值:
3.4 基于RF的毕业生就业预测模型
随机森林算法[13]是复合决策树的集成机器学习算法,采用“袋装”方法训练数据,该算法具有准确、高效,鲁棒等优点。算法的数学模型公式如式(4):倍率N为:
将数据集按照9∶1 的比例分为训练集和测试集。对训练集数据进行ADASYN-SMOTE 过采样处理,然后使用随机森林模型进行训练。用测试集验证,对测试结果分析,并通过绘制学习率曲线的方式确定当参数n_estimators=90,min_samples_split=2时随机森林模型效果最优。
4 实验结果与分析
准确率作为传统分类器算法的判断依据,在不平衡数据集中单独使用没有实际意义。为了更科学地描述实验结果,本文采用AUC[14],F1-score[15],Accuracy 判断模型效果。AUC 的取值介于0.1 和1之间,值越接近于1 越好,相比于其他的评价指标更具有泛化性[16]。就业预测的重要目的是对未就业学生的准确全面预测,F1-score 是查准率和查全率的调和平均值,F1-score 越大,对未就业学生预测越全面准确;Accuracy 是分类器对正负样本总体的预测准确率,值越接近于1越好。
测试后的实验结果如表1 所示,由该表可知,运用ADASYN-SMOTE-RF 算法,F1-score 比原始数据-RF 提高11%,比ADASYN-RF 算法提高8%,比SMOTE-RF 算 法 提 高5% ,比ADASYN 和SMOTE-RF[10]算法提高6%;Accuracy 值和AUC 值均最大,该结果充分说明了ADASYN-SMOTE-RF模型在对不均衡就业数据预测方面的精度和泛化能力均最强。
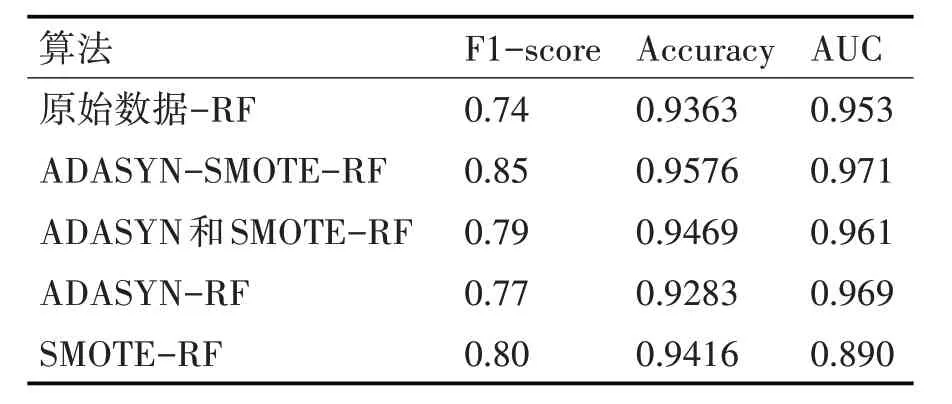
表1 实验结果表
5 结语
本文使用ADASYN-SMOTE 算法生成和扩充小样本数据,使用随机森林集成算法建立高职毕业生就业预测模型,实验结果表明,相较于未做特征选择,未进行样本均衡处理的随机森林模型,ADASYN-SMOTE-RF 算法能够明显提高模型预测的准确率、大幅度提升模型的F1-score 值、较为准确全面的预测未就业学生,从而能够更好地满足学校就业预测的实际需要,为提升高职学生就业率提供了坚实的科学依据。本文的后续工作主要有将ADASYN-SMOTE 与其他欠采样方法集成,以研究集成方法在高职学生就业预测方面的性能是否会比单个ADASYN-SMOTE过采样效果更好。

