基于RRT 改进算法的AGV 路径规划*

程 满 杨光永 徐天奇 黄卓群 刘 叶

（云南民族大学电气信息工程学院 昆明 650500）

1 引言

自动导引车（AGV）在自动化、灵活性方面具有独特的优势，使AGV 成为智慧仓储，智能物流自动化上的最优选择。路径规划是AGV 的核心，所以设计合理高效的路径规划算法十分重要［1］。AGV的路径规划目标在于通过采用某个算法，在包含有各种障碍物的空间中，避开障碍物于自由空间中安全行驶，最终生成一条从起点到终点的无碰撞的安全路径。路径规划的核心是算法，算法的高效、安全、路径最优等指标经常作为算法优劣的衡量项。目前对于一些常见算法的分类主要有全局路径规划和局部路径规划；图搜索算法和几何结构搜索算法；传统算法和人工智能算法。因为算法本身某些方面的局限性，所以在面对不同问题或者不同环境的时候不同的算法及其改进算法被用来解决某些类型的问题，采取算法某些方面的优点，去粗取精的混合算法也越来越受到研究者的喜爱［2～3］。

RRT 算法于1998 年由Lavall 所提出的［4］，基于环境空间的随机采样点规划的一种算法，节点的扩展不需要预处理，建模简单，速度快并且是一种概率完备算法，同时在高维空间中表现优秀，受到很多研究人员的关注，各种改进算法也相继提出［5～11］。Lavalle 等随后又提出了双向随机树（bi-RRT）［12］，在起始点和目标节点同时生长两棵树，两个方向进行扩展，加快算法的速度；RRT-connect 算法又是在bi-RRT 算法的基础上引入了贪婪的思想；Frazzoli 等提出了RRT*算法［13］，在生成新节点的时候，通过比较代价替换父节点，随着迭代次数的增加生成的路径向最优路径逼近；Nasir 等提出RRT*-smart 算法，在损失算法的随机性的代价下获得收敛速度的提升；刘成菊等提出变步长的RRT算法，改变随机树扩展节点时候的步长，加快收敛速度［14～16］。

2 RRT算法的改进

针对RRT 算法的缺陷，本文的改进重点在于通过在扩展节点的时候采用贪婪的思想，对已经规划的好路径进行两次重新选择父节点和布线，使生成的路径接近于最优路径；加入启发函数，将目标节点也加入算法的考量范围，使RRT 算法的扩展具有方向性，不再盲目扩展；将节点的扩展集中在一定区域，剔除冗余节点，避免多余无用节点的反复扩展，加快算法的运行速度。

2.1 选择低成本树进行重新布线

当随机树在自由状态空间已经生成的时候，RRT 算法的规划器都是选择Xrand最近的Xnearest，并将Xnearest与Xrand连接起来，按照步长生成节点Xnew，不能保证算法的成本约束，当使用低成本树优化之后，规划器将低成本的节点连接起来，从起始点到当前节点保持距离成本的最小值，保障生成路径质量。

H 节点是最新生成的Xnew节点，Xnew的父节点Xnearest如图1 所示为E 节点，起始节点Xstart为A节点。如图1 所示，在第一次优化之前，节点路径为A-B-C-E-H，路径代价为11。现在进行第一次优化，以节点H为圆心，以一定长度为半径，作一个圆，将H 与I、F、G、K 连接，长度都为2，到达节点H有多条路径，例如：A-B-I-H、A-B-C-E-F-H、A-B-C-E-G-H、A-J-K-H。将这些路径包括之前未优化之前的那条原始路径的代价进行比较，选择最短的路径代价的那条路径并且将之前的父节点变换成最短路径的父节点，第一次优化后的路径如图2所示。

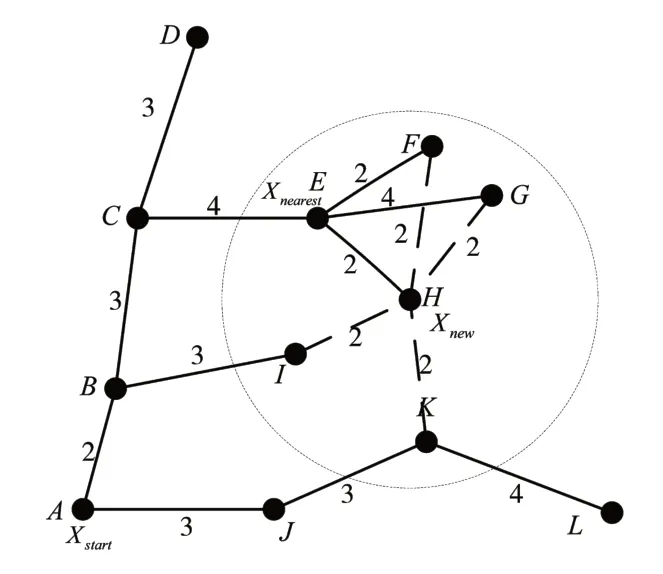
图1 第一次优化示意图

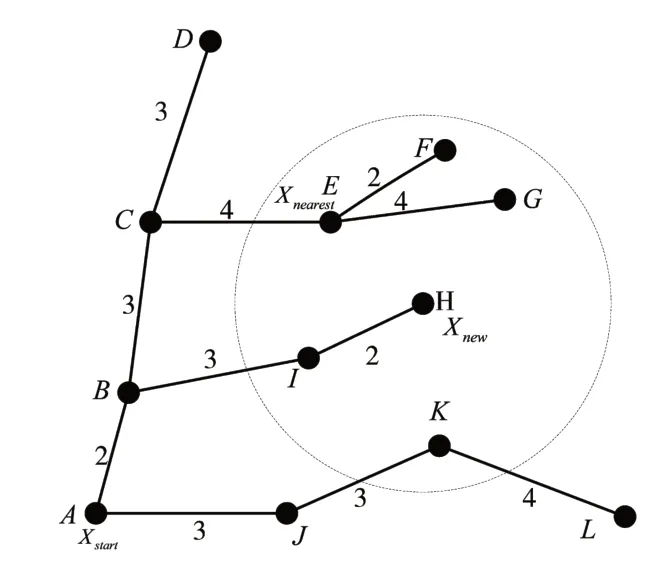
图2 第一次优化重新布线

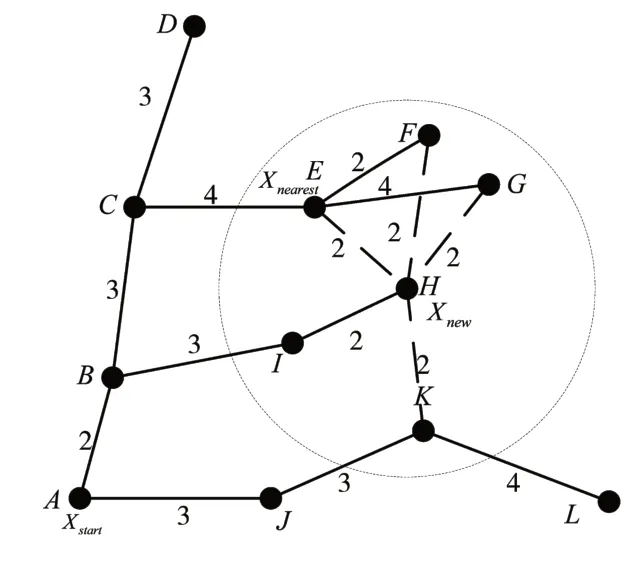
图3 第二次优化示意图

在图2 新路径代价为最短的A-B-I-H，此时代价为7。将之前的H 实连接线去掉，并将虚线所示的I 和H 的连接线变成实现，运用贪婪思想计算新节点设定一定值半径范围内的所有节点的代价值计算，取其中最小代价为所走路径，这样生成的路径比较接近于最优路径。第二次优化，重复第一次优化的步骤。

连接H-E、H-F、H-G、H-K 比较到达E、F、G、K这四个节点，通过现有树的代价和通过H节点到达的代价，选择代价小的方式到达，重新布线。第二次优化如图4所示。

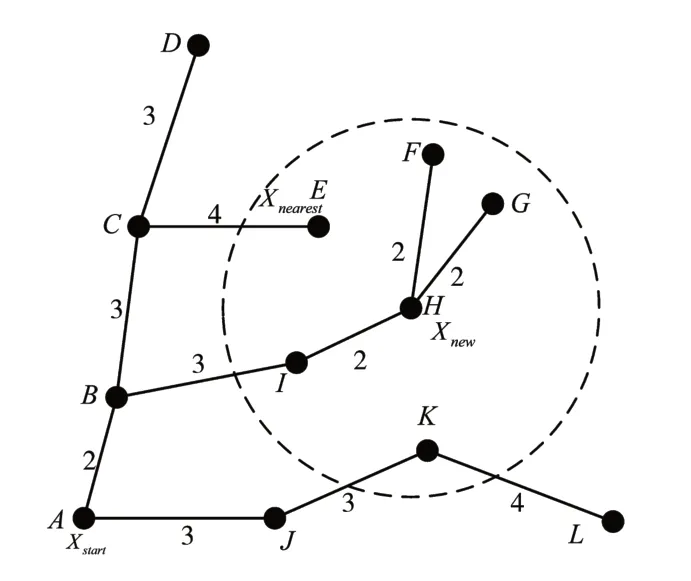
图4 第二次优化重新布线

2.2 启发式变步长

传统的RRT 算法并没有将目标节点考量进去，树的扩展是随机的，每次扩展的步长也是一个固定的步长，现在改进的RRT 算法将目标节点加入考量范围，树的扩展具有了方向性，扩展的方向不再仅是由随机方向的随机点Xrand单独控制，而是随机方向的Xrand和目标终点的Xend共同控制。新的步长扩展公式为

当无障碍物在行驶的路径附近时，β>α，引导树的扩展方向更多的朝着目标节点，可以加快目标节点的搜索速度；如果发现障碍物，改变α和β的值，此时α>β，树的搜索更多地朝向随机搜索方向，α和β两个值大小的变化，有助于整个路径规划系统更好地逃避出局部最小值。

2.3 正态分布

当随机变量服从数学期望为μ和方差为σ2的正态分布时，记作N(μ,σ2)。概率密度函数表示为

二维标准正态分布为

若用随机变量v来表示，v=[xy]T即：

由标准正态分布推广到一般v=A(X-u)。

将正态分布加入算法中，主要是为了减少相对状态空间，将树的扩展限制在某些区域，使规划的效率提高。本文所使用的多元正态分布公式：

其中Σ 是协方差矩阵，Σ=UΛUT，u1,u2是协方差矩阵的特征向量，λ1、λ2是相应的特征向量的特征值。

图5 起点位置为（20，40），终点位置为（90，40），可以有效地将随机采样点集中在一定区域。该算法以起点开始，随迭代增加，树开始扩展，通过规划生成Xnew节点，此节点的扩展不仅是在随机点的方向上，而且偏向目标区域，正是因为具有这种偏向性，可以更快地找到第一个解，当第一个解决方案生成之后，用这条路径作为参考，通过正态分布生成样本点，最后找到一条高质量的路径。如上图所示，图中的正态分布的形状取决于两个因素，分别为Cbest和Cmin。整个正态分布的区域可以表示为长度为Cbest，宽度为，其中Cbest是所有可行解决方案中成本代价最小的，Cmin是起始点与目标节点之间的欧氏距离，λ1=Cbest/2 ，，若是无障碍空间，那么λ2的值会降到0，也就是可行路径的最优路径此时就是最短路径，直接生成一条直线连接起始点和终点。

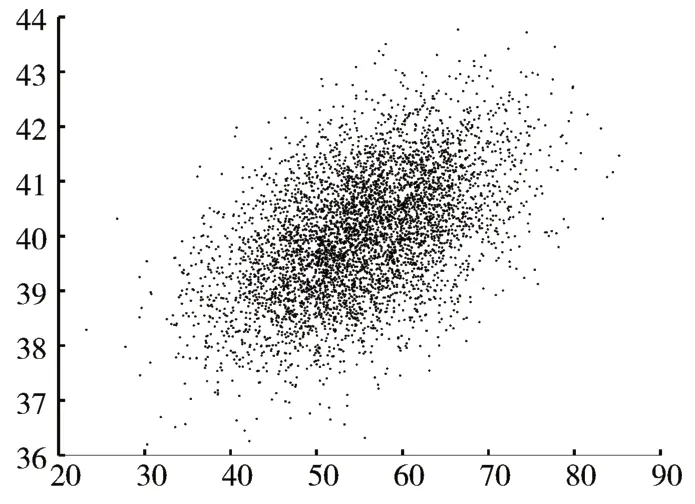
图5 正态采样点分布图

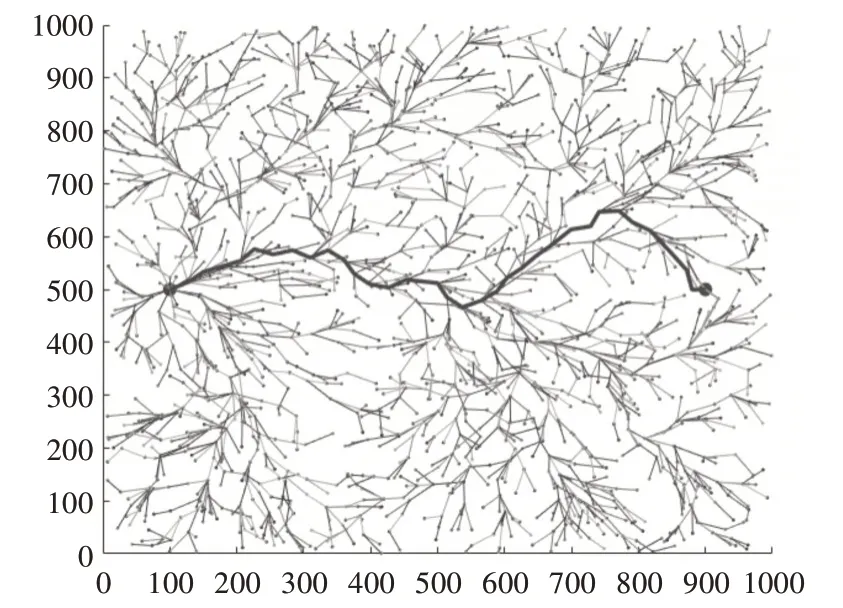
图6 无障碍RRT算法仿真

图7 无障碍RRT改进算法仿真

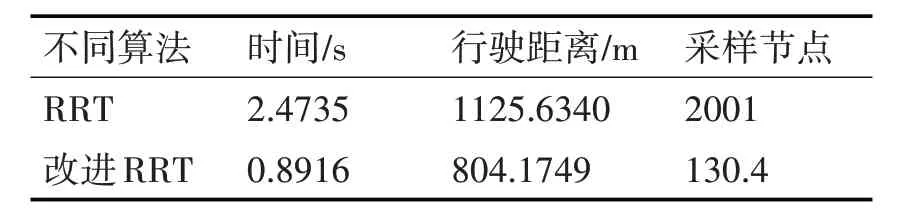
表1 图6和图7参数比较

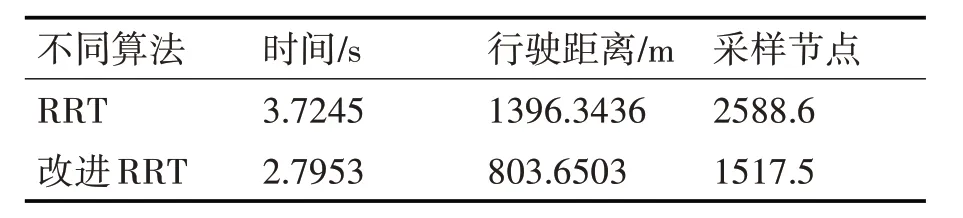
表2 图8和图9参数比较

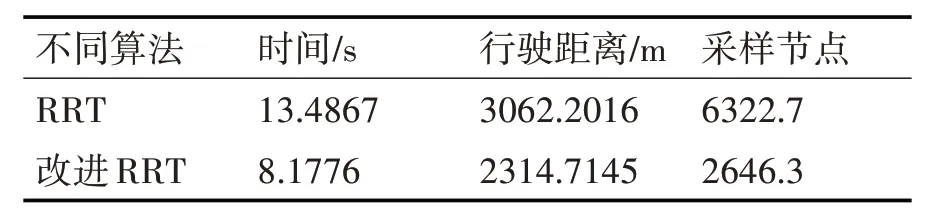
表3 图10和图11参数比较

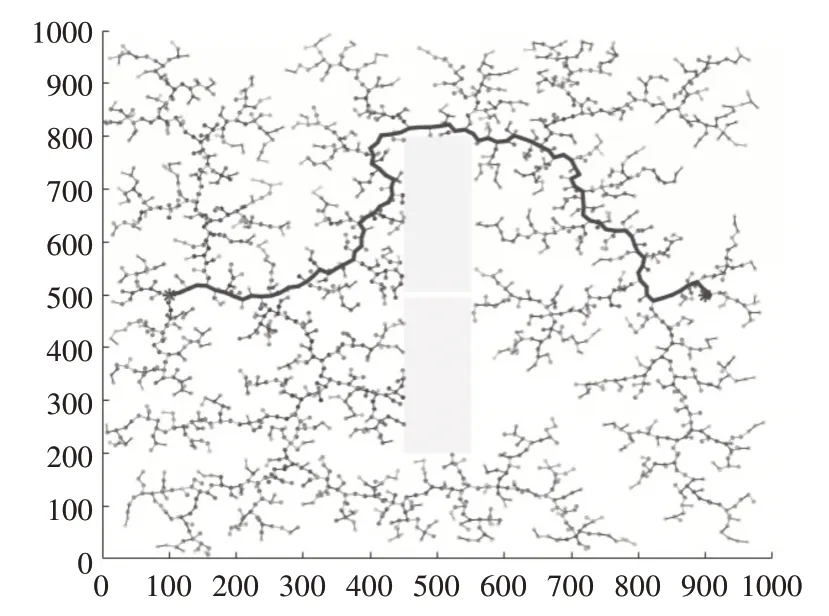
图8 狭窄通道RRT算法仿真

图9 狭窄通道RRT改进算法仿真

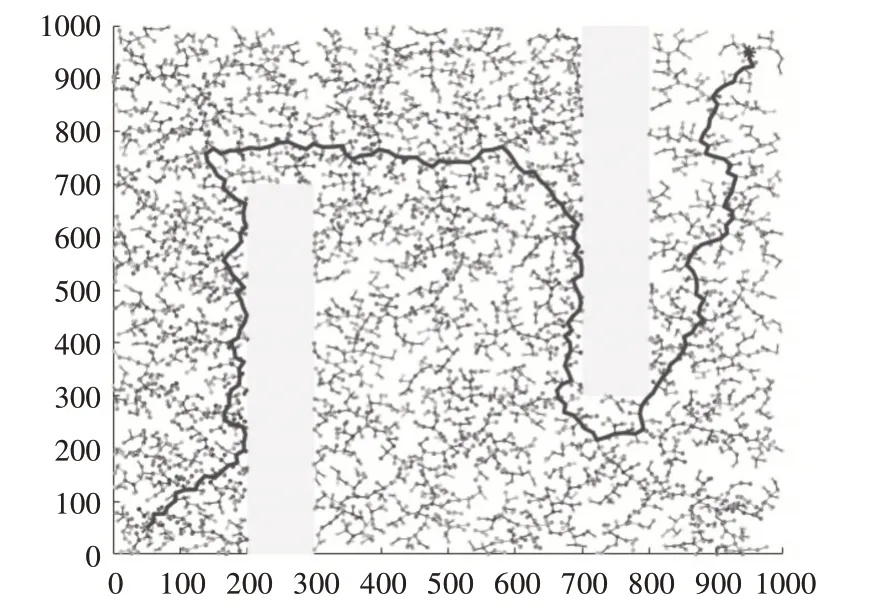
图10 普通环境RRT算法仿真

图11 普通环境RRT改进算法仿真

3 改进算法仿真对比实验

所有的对比仿真实验都是在个人PC 上完成的，基于Matlab-R2018a，环境地图大小设置为1000×1000 。个人PC 硬件配置：处理器Inter（R）Core（TM）i7-10875H、内存为16G、系统版本为Windows10。

3.1 无障碍物环境对比实验

为了看出更直观的效果，首先在无障碍物环境中进行实验，起点设置为（100，500），目标节点设置为（900，500）。RRT 算法的步长为15，实验环境的地图单位为m，时间单位为s，无障碍环境下的仿真实验的迭代次数设置为2000次。

由于算法的随机性，将实验50 次的数据取其平均值，改进算法相较于传统算法来讲，运行效率大大提高，算法运行时间缩减了63.95%，距离相较于理想距离更加接近，采样节点减少了93.48%，行走的线路较于传统算法而言，行驶路径较平滑，易于跟踪行驶。

3.2 狭窄通道环境对比实验

当我们探索的路径需用通过一个很狭窄的通道时，过于狭窄的通道会导致我们路径被碰到的概率极其之低，找到路径时间的长短很随机，全靠运气。有时运气好，RRT很快就在狭窄通道找到了路径，运气差的时候，就可能一直无法通过。目前有好多学者都在对RRT 算法进行改进，目的在于解决通过狭窄通道这个难题。改进算法将目标节点加入到了启发的一部分，加强了算法通过狭窄通道的能力。以下仿真实验设置一个宽度只有10m 的狭窄通道。

改进后的算法是启发式变步长的生长，当扩展开始，无障碍物时候，主要考虑目标节点的启发式生长，当在障碍物附近的时候，主要考虑随机生长状态，可以很好地避障的同时穿过狭窄通道。由于算法的随机性，取50 次试验的平均数据，算法的运行时间减少24.95%，行走的路径接近于最短路径，采样节点减少了41.38%。

3.3 普通环境对比实验

改进后的算法相较于传统算法而言，效率大大提高，运行时间减少了39.37%，行驶距离减少了24.41%，采样节点减少了58.15%，行驶路径较于传统算法而言，路径较为平缓，转弯的次数较少，易于跟踪行驶。

4 结语

改进后的算法在AGV 的路径规划中采用了正态分布的思想，将节点的随机分布探索范围集中在正态分布的区域，避免了无效冗余节点的探索，大大提高算法的执行效率。由传统的固定步长变成了变步长启发式生长，动态调整两个分量的大小，以达到不同环境下的侧重点不同，距离目标过远，重点在于目标节点的启发生长，当附近存在障碍物时，那么此时的重点在于随机生长，可以有效地避障，避免局部最小值。在Matlab上完成了仿真对比实验，验证了算法改进后，生成质量更高的路径，探索节点减少，效率提高，生成较平滑的路径有利于跟踪行驶，同时在面对狭窄通道时也可以快速顺利通过。