基于用户聚类和时间隐语义模型的推荐算法研究*
吴 祺 聂文惠
(江苏大学计算机与通信工程学院 镇江 212000)
1 引言
随着社会的发展和网络技术的不断进步,信息数据呈现爆发式增长,传统的协同过滤推荐算法已经无法满足人们日常的需求,人们无法从海量的数据中快速获得自己想要的信息,即产生“信息过载”问题[1]。如何更准确更快速地帮助用户获取有效信息成为当前研究的热点,个性化推荐也就应运而生。
协同过滤算法[2]是目前推荐系统中应用最为广泛最为成熟的算法之一,它的核心思想是通过寻找拥有相同兴趣爱好的用户继而通过相似用户的兴趣爱好为该用户推荐可能感兴趣的信息。随着用户数量和物品数量呈现指数型增长,用户对物品的评分数据变得稀疏,传统的协同过滤算法在处理稀疏矩阵时推荐准确率较低[3]。
用户聚类是通过聚类算法将用户对象的集合分成由类似对象组成的多个类的过程。K-means算法是常见的聚类算法之一,其将具有相同属性特征的用户归为一类[4],这样一方面使得无历史行为的新用户获得推荐,即解决“冷启动”问题,另一方面降低了矩阵稀疏程度和矩阵规模,提高隐语义模型预测的准确度。
针对数据稀疏性问题,国内外学者提出多种解决方法。Su、Khoshgoftaar 等[5]用线性回归、均值填补和贝叶斯分类等多种方法以缓解用户-评分矩阵的稀疏问题,但使用均值填补稀疏矩阵给用户评分预测带来较大的误差;Hao、Li等[6]提出利用用户评分偏好相似性和特征矩阵来预测商品评分,该方法当数据非常稀疏时,算法的稳定性和准确性下降。在解决稀疏性问题中矩阵分解算法也具有较好的效果,其中SVD 算法是最早的矩阵分解算法,由Billsus 等[7]将其引入推荐系统。该算法计算复杂度较高,难以应用于大规模评分矩阵[8]。2006 年Simon Funk 在博客上发布Funk-SVD 算法,后来被称为隐语义模型(LFM)[9]。隐语义模型是近几年推荐系统领域较为热门的话题,它主要是利用矩阵分解建立隐含特征与用户和隐含特征与物品之间的关系,进而通过隐含特征将用户与物品联系起来[10],最终预测用户对物品的偏好,大大缓解了协同过滤算法由于数据稀疏引起的推荐准确率低的问题。当然该模型还存在着一些不足,如没有考虑时间因素对用户评分的影响。
本文将K-means 聚类算法和隐语义模型相结合,提出基于用户聚类和时间隐语义模型的推荐算法(K-T-LFM)。该算法既克服了新用户冷启动和数据稀疏性的问题,同时也考虑了时间因素对用户兴趣的影响。
2 基于用户聚类和时间隐语义模型的推荐算法
基于用户聚类和时间隐语义模型的推荐算法(K-T-LFM)融合了K-means 聚类算法和隐语义模型,本文首先介绍用户聚类和隐语义模型,然后提出使用融合时间函数的隐语义模型对缺失矩阵进行填充,基于目标聚类用户通过协同过滤算法产生推荐。
2.1 用户聚类
用户聚类主要是根据用户的特征属性对用户进行聚类,从而找到相似的用户群体。日常生活中具有相近特征属性的用户往往会有相似的兴趣爱好,不同特征属性类别的用户往往兴趣爱好差异性较大[11]。考虑到用户的特征属性是相对客观稳定的,本文通过引入用户特征进行聚类来降低不相关用户对目标用户的影响。同时在用户初次登陆APP应用时,通过用户的属性特征聚类可以解决冷启动的问题,为该用户推荐相似用户的兴趣爱好。
考虑到用户的特征属性比较多,本文依据用户以下几个主要特征进行聚类[12]:
1)性别。不同性别的人大体上兴趣偏好差异很大,男女可以分别记为{1,2};
2)年龄。人在不同年龄段有不同的生活履历和遭遇,因此不同年龄的人对生活的态度也不同,可以将年龄段分为12 岁以下,13-17 岁,18-29 岁,30-39 岁,40-49 岁,50-59 岁,60 岁以上,分别记为{0,1,2,3,4,5,6};
3)职业。不同职业的人有不同的价值观念和兴趣爱好,看待事物的角度也不同,按照职业的不同分别记为{0,1,2,…,n}。
建立用户特征数据表,记录用户的性别,年龄,职业信息,然后采用最大-最小准则算法确定初始质心改进的K-means算法进行聚类。
改进的K-means算法用户聚类过程:输入:用户特征数据集u,聚类个数k
输出:k个依据用户特征数据划分的聚类
1)定义聚类的个数k;
2)随机选择一个点作为质心,选取距离这个点最远的点作为第二个质心,然后计算每个点到两个质心的距离,选取距离较小的加入到集合V 中,在集合V 中选取距离最远的点作为下一个质心,以此类推,直至选择第k个质心;
3)计算其它点到每个质心的距离,选择距离最近的质心作为一类;
4)计算每个聚类的中心点,作为新的质心;
5)Repeat 3),4);
6)达到最大迭代次数或者质心基本不发生变化则用户聚类结束。
通过用户聚类不仅解决了用户初次登录冷启动的问题,同时通过降低用户数据的维度,缓解数据稀疏性,提高了使用隐语义模型预测的准确率。
2.2 隐语义模型
隐语义模型主要是针对SVD 算法填充稀疏矩阵需要大量存储空间的缺点改进而来,它能有效地挖掘用户与物品间的隐藏关系。将其应用在推荐系统的预测中具有预测精度高和占用内存小的优点。该模型通过矩阵分解将用户评分矩阵分解为两个低维评分子矩阵,分别为用户隐含特征矩阵和物品隐含特征矩阵:
其中P∈Rf×m,Q∈Rf×n分别为用户隐含特征矩阵和物品隐含特征矩阵。用户u 对物品i的评分预测公式为
其中rui表示用户u对物品i的评分,puf表示用户u的兴趣和第f个隐类的关系,qif表示电影i和第f个隐类的关系。
定义其损失函数为
其中λ(| |pu||2+||qi||2)是为了防止过拟合,λ是正则化参数。但是随着时间的推移,用户的兴趣爱好可能发生变化,进而影响了推荐的准确率。
2.3 时间隐语义模型
2.3.1 时间权值的选择
德国心理学家艾宾浩斯提出人类遗忘曲线[13],主要依据是:随着时间的推移,人的记忆会随之发生变化,曲线描述了人类大脑对事物的遗忘规律,用户对新事物的兴趣随着时间推移同样遵循遗忘规律。
考虑到时间因素对用户兴趣的影响,采用指数时间函数来表示,突出用户近期兴趣偏好所占的权重[14],考虑到存在一些经典的物品随着时间推移依然受欢迎,所以在传统的指数函数上进行了一定的优化,使得随着时间的推移,用户对物品的兴趣并不会最终趋近于0。该时间函数定义如下:
其中,Tu,i表示用户u对项目i的评分时间,Tk表示过去的某一个固定时间,时间函数f(tu,i)的取值范围是(0.5,1),表示用户兴趣的时间权重。
2.3.2 融合时间因素的隐语义模型
传统的隐语义模型在预测用户评分时没有考虑时间因素的影响,因此在用户隐含特征子矩阵加入式(4)的时间函数。结合式(2)用户u 在tu,i时间点对物品i的评分预测公式为
其中,puf(tu,i)表示随时间变化的用户偏好的特征子矩阵,其值用以下公式表示:
其中,a为调节时间函数的参数。
本文在用户隐含特征子矩阵中加入时间函数,考虑了用户对于未评分物品的兴趣随时间产生的变化,避免了填充缺失矩阵时使用全局平均值或评分中位值带来的误差。
2.4 基于用户聚类和时间隐语义模型的推荐算法
本文结合K-means 算法和隐语义模型进行推荐,基于用户的属性特征通过改进的K-means算法对用户进行聚类,对每个用户聚类使用融合时间函数的隐语义模型进行预测,最后结合传统的协同过滤推荐算法进行推荐。
基于用户聚类和时间隐语义模型的推荐算法(K-T-LFM)具体流程如下:
输入:用户u,评分矩阵R,用户u 对物品i 的评分时间戳t,用户分类的簇数k。
输出:向目标用户推荐的N个物品。
步骤1:结合用户的特征属性使用最大-最小准则改进的K-means算法对用户进行聚类,将具有相似特征属性的用户聚为一类;
步骤2:根据用户聚类构建相应的用户-物品评分矩阵,在各评分矩阵中使用融合时间函数的隐语义模型,对聚类中数据缺失的用户-物品评分矩阵进行填充预测;
步骤3:基于完成填充预测的用户-物品评分矩阵,计算用户间的相似度,选出M 个最相似用户作为最近邻居;
步骤4:根据M 个最近邻居的评分数据来预测当前用户u对未评分物品的评分数据;
步骤5:选择预测评分topN 的物品向用户推荐。
3 实验与分析
3.1 数据集简介
本文采用的数据集是来自美国明尼苏达大学GroupLens 小组提供的MoviesLens 数据集[15]。主要是使用MovieLens 数据集中的ratings.data 和movie.data两个文件数据,其中rating.dat文件包含了6040个用户对3900 部电影的1000209 条评分,users.dat文件包含6040 个用户的性别、年龄、职业等信息。整个数据的评分矩阵稀疏度为94.88%。实验过程中,将数据集按照70%和30%的比例分为训练集和测试集。
3.2 评价指标
本文采用的评价指标是均方根误差(RMSE),RMSE[16]是衡量系统性能的一个重要指标,RMSE值是预测值与真实值偏差的平方与观测次数n 比值的平方根,用来衡量观测值同真值之间的偏差,因此RMSE 的值越低表示算法的预测准确率越高。其公式如下:其中,|U|是测试集提供的评分总数量,rui是用户u对物品i的实际评分,rui是预测评分。
3.3 实验结果
1)隐特征维度L对RMSE的影响
实验中通过确保LFM 模型其它参数不变的情况下(其中学习速率为0.02,正则化参数λ=0.05,迭代次数n=50,调节参数a=0.5),改变LFM 的隐特征维度L,观察预测误差RMSE的值,实验分布曲线如图1所示。
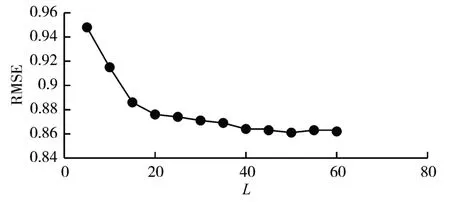
图1 不同隐特征维度L对RMSE影响
由图1 可以看出,当隐特征维度小于40 时,RMSE 值随着隐特征维度的增加而减小,当隐特征维度L 大于40 之后,LFM 模型的RMSE 的值趋近于稳定,所以实验中设置L为40。
2)调节参数a和迭代次数n对RMSE的影响
实验中将LFM模型的隐特征维度L设置为40,学习速率为0.02,正则化参数λ=0.05,观察调节参数a 和迭代次数n 对RMSE 的影响,实验分布曲线如图2。

图2 不同调节参数a对RMSE的影响
由图2可以看出,随着迭代次数n的增加,调节参数取0.5 时RMSE 始终最低,且迭代次数n 在40之后值趋于稳定,所以设置LFM 模型的调节参数为0.5,迭代次数为50。
3)聚类个数K对RMSE值的影响
实验中在保持设定的LFM 模型参数不变的情况下,改变聚类的个数K,观察聚类个数K 对RMSE的影响,实验分布曲线如图3。

图3 不同聚类个数K对不同算法RMSE的影响
图3 可以看出,在保持目前参数的情况下,随着聚类个数的增加,考虑时间因素的算法(K-T-LFM)的RMSE 值始终低于未考虑时间因素的算法(K-LFM),所以考虑时间因素的隐语义模型整体性能优于传统的隐语义模型,并且聚类个数在20~25之间准确率最高,设置聚类个数为25。
4)不同算法的RMSE值比较
实验中在保持设定的LFM 模型的参数和聚类个数K 不变的情况下,改变最近邻居数M,观察随着最近邻居数M 的增加不同算法的RMSE 值,实验分布曲线如图4。
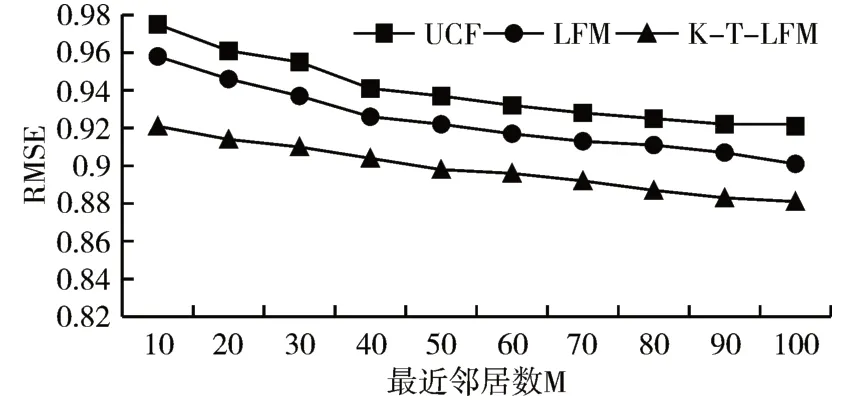
图4 不同邻居个数下不同算法的RMSE比较
采用多种算法对数据集进行测试,随着最近邻居个数M 的增加,从图4 中可以看出,本文提出的基于用户聚类和时间隐语义模型的推荐算法(K-T-LFM)的RMSE 值均小于隐语义模型(LFM)和基于用户的协同过滤算法(UCF),可以说明其在准确率方面能达到比较好的效果,优于其它两种算法。
4 结语
针对传统推荐算法数据稀疏情况下推荐准确率低的问题,本文提出融合K-means算法和隐语义模型来预测填补稀疏矩阵,同时考虑时间因素对用户的兴趣偏好的影响,在隐语义模型中融入时间函数,提出基于用户聚类和时间隐语义模型的推荐算法(K-T-LFM)。通过实验对比,本文提出的混合推荐算法相较于其它算法具有较好的准确度。后续研究工作中考虑将物品信息融入算法中,以进一步提高算法推荐的准确度。

