初中数学平面几何题型解决策略

卜建红

摘 要：勾股定理展示出直角三角形的三边关系，是对平面几何问题进行有效解决的重要方式，且在现实生活中得到广泛运用.鉴于此，本文主要对勾股定理解决平面几何题的策略进行探讨.

关键词：初中数学；平面几何题；勾股定理；解题

初中数学的课堂教学中，教师需注重数学思想与方法的结合，在深化学生对知识理解的同时，促使学生由数学知识的学习中体会到解题思想与方法.勾股定理作为初中数学学习中的重要定理，其既能体现出直角三角的三边关系，又能促进代数和几何的有效联系，定理内容能充分呈现出“数形结合”的数学思想.本文主要立足于勾股定理的经典题型，对其进行剖析，以促使學生充分体会到数学解题中用到的数学思想，从而实现高效解答平面几何题型.

1 勾股定理概述

勾股定理主要指直角三角形当中，两条直角边平方和与斜边平方相等，数学公式为a2+b2=c2（a并为直角边，c斜边）.初中数学开展勾股定理教学通常有着显著价值，即：（1） 证明勾股定理属于论证几何的开端；（2） 勾股定理是第一个将数和形有效联系起来的一种定理，也就是第一个将几何和代数有效联系的定理；（3） 勾股定理的运用，引出了无理数，可深化人们对于数的理解与掌握；（4） 勾股定理是第一个提供了不定方程有效解决的方式，并引出费马大定理；（5） 勾股定理属于欧式几何的一项基础定理，有着显著的实用价值，被称作为几何学的研究基石，且在高等数学以及其他领域得到了广泛运用.除此之外，勾股定理的另一个价值就是解常规的三角形，更多是在常规三角形当中引出某条边的高，将其分成两个直角三角形，且由此引出了正弦定理与余弦定理，将其运用于初中数学几何题型解答中，通常能够使相关题型得到有效解决.

2 以“勾股定理”解决平面几何题型的策略

2.1 利用勾股定理求线段的长

例1 图1所示，湖面上，有一朵莲花，其高出水面3尺，一阵风吹过，莲花被吹至一边，花朵与水平一致，已知莲花移动的水平距离是6尺，请问水深是多少？

解析：本题主要是通过列方程的方式进行问题解决，关键就是明确其已知量与未知量，及其等量关系.

依据题干可知，已知AB=3，A1B=6，AC=A1C，其未知量是BC，此时，设水深BC是x尺，在直角三角形A1BC当中，依据勾股定理可得：A1B2+BC2=A1C2，列方程为：62+x2=（x+3）2，求解得出：x=4.5，也就是水深为4.5尺.

评析：本题的解决是先将实际问题转变成数学问题，依据题意进行数量关系的分析，依据示意图呈现的已知量和未知量，明确其等量关系，再设未知数，通过勾股定理列出方程进行求解，这是运用勾股定理求解线段长的典型案例.

2.2 利用勾股定理求面积

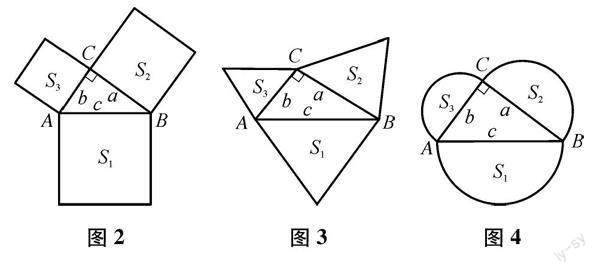
例2 （1） 图2所示，分别将直角三角形三边向外延伸为正方形，其面积分别是S1、S2与S3，已知S2、S3的值为9与4，求取S1.

（2） 图3所示，分别将三角形的三边向外延伸为等边三角形，其面积分别是S1、S2与S3，求取S1、S2、S3存有的数量关系是多少？

AC′G3当中，依据勾股定理可知：AG3=AC′2+C′G23=62+12=37.

第四种：由左上侧进行展开，图11所示，位于长方体当中，可得出：EF′=EF=AB=4，F′G4=FG=BC=2，AF′=AE+EF′=1+4=5.在直角三角形AF′G4当中，依据勾股定理可知：AG4=AF′2+F′G24=52+22=29.

综上所述，由于5＜29＜37，因此，蚂蚁爬过的距离最短是5.

5 结束语

综上所述，勾股定理是联系数和形一个重要定理，经过勾股动力的学习与运用，学生通常能深刻体会到其中的数学思想，并实现知识整合以及学习能力提高的效果.鉴于此，数学教师在具体教学时，需关注到数学中常见的勾股定理运用方法，并加以整理，从而使学生在解题时，能够灵活运用勾股定理解决相关几何题型.

参考文献：

［1］ 卢崇连.巧用勾股定理，妙解数学问题［J］.现代中学生（初中版），2021（22）：3940.

［2］ 林小波.初中数学中勾股定理的解题策略［J］.现代中学生（初中版），2021（20）：3132.

［3］ 罗俊.初中数学勾股定理问题解题探究［J］.现代中学生（初中版），2021（10）：3940.

［4］ 肖力.勾股定理在初中数学中的应用特点探讨［J］.现代职业教育，2018（20）：236.

［5］ 吴叶科.关于勾股定理教学中的重点问题剖析［J］.数学教学通讯，2016（29）：2324.