基于人工神经网络的零差K 参数成像监测微波热消融凝固区研究

刘俊汝，李思楠，吴水才

（北京工业大学环境与生命学部，北京 100124）

0 引言

微波热消融是临床治疗肝细胞癌的主要方法之一，该技术通过加热引起细胞损伤，并形成一定体积的凝固性坏死区域[1]。为了降低肿瘤复发的风险，在手术过程中需要利用成像技术监测热消融产生的凝固区，凝固区需要完全覆盖肿瘤，并在各个方向形成5～10 mm 的边界[2-3]。超声成像技术作为热消融过程中监测凝固区的成像技术具有的优点包括连续实时成像能力、成本相对较低、在评估热消融治疗效果时与动态CT 具有高度一致性[4-6]。消融过程中，随着温度的升高，组织的微观结构变化会带来声学性质的变化，传统的B 超成像可以利用超声背散射信号的幅值提供高分辨力和高帧速率的图像，但由于加热过程中气泡活动会在B 超图像中产生后方声影，使其难以确定消融区的形状和大小[7]。而定量超声成像技术可以利用声学特性对热消融区域提供定量的评估，具备区分消融区和正常组织的潜力[8]。

常用于监测凝固区的定量超声技术包括包络统计参数成像[9-13]、回波去相关成像[14-18]、超声衰减系数成像[7，19]、超声信息熵成像[20]等。超声背散射信号是由每个散射体贡献的散射波的空间总和，包含散射体的形状、大小、密度和其他特性相关的有价值的信息，具有一定的随机性[21-23]。在声学上，肝实质可以模拟为大量散射体组成的微观结构。热消融过程中产生的气泡活动和细胞坏死会导致散射体浓度或排列发生变化。因此，肝组织显微结构的局部空间分布可以根据超声背散射信号的包络统计量（即信号振幅分布）进行评估[23]。当换能器分辨单元中散射体的数量密度增加时，包络统计量呈现出从前瑞利分布到瑞利分布的变化[24]。通常，Nakagami 分布模型和零差K 分布模型是2 个最常用的超声背散射广义统计模型，利用2 种分布模型的参数可以将气泡变为有效信息，表示散射体的变化。由于零差K 分布是用广义积分表示的，参数估计方法较为复杂，大部分研究利用Nakagami 分布模型进行近似[25]。Nakagami 分布模型利用m 参数表示散射体浓度的变化，有很多研究已将其应用于凝固区的监测中，但其在凝固区和正常组织之间会存在边界效应，容易受到气泡和声学伪影的影响，在这种情况下，边界的m 参数值较低[12]。零差K 分布有效利用α 参数和k 参数描述组织中的散射，参数具有物理意义，偏度、峰度可以测试包络信号是否遵循瑞利分布，Hruska 等[26]首次提出RSK 估计器，利用信噪比、偏度、峰度3 个分类器估算α、k 参数。Destrempes 等[27]首次提出XU 估计器，利用单调函数二分法基于强度一阶矩和两阶对数矩计算零差K 分布模型的参数。Song 等[13]将噪声辅助相关算法与零差K 参数成像算法相结合，首次将零差K 成像用于监测微波热消融产生的凝固区，并且证实了在监测肝组织微波热消融凝固区时，XU估计器优于RSK 估计器[28]。Zhou 等[29]提出一种基于人工神经网络（artificial neural network，ANN）估算零差K 分布参数的估计器，结果表明，ANN 估计器比RSK 和XU 估计器计算准确性更高、计算速度更快。ANN 估计器在组织表征方面具有很大的潜力，已经在脂肪肝变性、肝纤维化评估中得到了应用，但其在凝固区监测方面还未有应用[29-30]。

基于此，本研究利用ANN 估计器估算零差K分布的α、k 参数，并与多项式拟合（polynomial approximation，PAX）技术相结合对微波热消融产生的凝固区进行定量评估。同时在不同消融功率、持续时间下，通过ROC 曲线、Dice 系数和Jaccard 系数，对比XU和ANN 估计器估算零差K 分布模型参数PAX 成像监测微波热消融的性能。

1 研究方法

1.1 实验数据采集

本文对新鲜的离体猪肝进行微波热消融实验，采集超声背散射信号来对比ANN、XU 估计器监测凝固区的性能。实验平台设置如图1 所示，实验设备包括微波消融仪（KY-2000，南京康友有限公司）、水冷式微波消融针（KY-2450B，南京康友有限公司）、便携式超声扫描仪（Terason T3000，美国Terason 公司）、线性阵列换能器（12L5A，中心频率为7.5 MHz、通道数为256、脉冲长度约为0.7 mm，美国Terason公司）、用于盛放离体猪肝标本的丙烯酸盒子以及用于固定换能器的支架。

图1 实验平台设置图

实验开始前，将离体猪肝放置在0.9%的氯化钠溶液中浸泡进行去气泡处理。然后利用B 超成像避开大血管和筋膜对离体猪肝进行扫描选取样本，将离体猪肝放入丙烯酸盒中进行消融实验。将水冷式微波消融针插入离体猪肝时，消融区最长直径对应的消融针发射点放置在线性阵列换能器正下方，以保证换能器采集的平面为当前功率、时间下消融面积最大的截面。

实验中，利用自写的程序以2 帧/s 的速率采集原始的超声背散射信号，信号数据以.bin 格式存入超声扫描仪硬盘中，信号矩阵大小为1 558（采样点数）×256（扫描线数）。控制消融功率和持续时间分别为80 W 1 min、70 W 2 min、60 W 3 min，3 组实验各采集16 例超声背散射信号。实验结束后，沿线性阵列换能器采集的平面切割消融后的离体猪肝，拍摄组织切片的图片。利用Image J 软件对组织切片的图片进行处理，以针尖为中心取3 cm×3 cm 大小的感兴趣区。由专家手动勾选出感兴趣区中凝固区的范围，然后做二值化处理，将凝固区为1、正常组织为0 作为金标准。

1.2 理论依据

零差K 分布的概率密度函数fHK（A）被定义为

式中，A 代表超声背散射信号包络的振幅；变量x 仅用于积分；J0（·）表示第一类零阶贝塞尔函数；ε2和2ασ2分别为背散射信号中的相干分量和漫散射分量；散射体聚类参数α 表示每个分辨力单元中有效散射体的个数。导出的k 参数代表相干信号与漫散射信号能量的比率，可用于描述散射体的结构水平或周期性，相关公式如下：

零差K 分布的概率密度函数十分复杂，没有封闭的函数表达形式。目前，估算零差K 分布的α 参数和k 参数的方法包括XU 法[27]、RSK 法[26]和ANN 法[29]。

1.2.1 XU 法

式中，XHK、UHK分别表示X、U 统计量的理论值；arg min表示使|UHK-U|取最小时的自变量取值。利用二分法估计满足方程的最优参数ε2、σ2、α，然后根据公式（2）计算得到k 参数[27]。为提高计算效率，本文将αmax设置为40.5。

1.2.2 RSK 法

RSK 法基于包络振幅信噪比R、偏度S、峰度K的任意阶矩v（v 为矩数）的水平曲线估计，关系如下：

当v 为固定值时，Rv、Sv、Kv是关于α、k 参数的函数，将零差K 分布预测的R、S、K 理论值与包络信号计算的估计值取等，可以估计出α、k 参数。本文中设置v=2。

1.2.3 ANN 法

ANN 法利用蒙特卡罗仿真对每一组α、k 参数值生成符合零差K 分布的独立同分布（independent and identically distributed，IID）包络信号样本，作为模型的训练集。通过公式（3）～（8）计算训练集中每个样本对应的X、U、R、S、K 5 个特征参数作为模型的输入。训练ANN 模型后得到α、k 的参数估计作为模型的输出。

在生成IID 包络信号样本时，为了消除σ 参数的影响，将信号功率的平均值限制为1：

式中，Xi和Yi分别代表单位高斯分布的IID 样本和伽马分布的样本，i 表示生成的样本数。本文中i=3 158，对应于5 倍超声换能器脉冲长度。IID 包络信号样本的参数范围为：lg α∈{-1.00，-0.99，…，2.00}、k∈{0.00，0.01，…，2.00}。因此，训练集的大小为60 501×3 158。

ANN 模型为4 层前反馈反向传播网络，第一层为5 个神经元组成的输入层，分别对应5 个特征参数；2 个隐藏层的神经元个数分别为30、10；第四层为2 个神经元组成的输出层，分别对应lg α、k参数的估值。具体的ANN 估计器设置可参考文献[29]。

1.3 超声背散射信号零差K 参数成像

通过MATLAB R2019a 软件（美国The MathWorks公司）对实验采集的超声背散射信号进行处理，构建B 超图像。对去噪后的超声背散射信号分别基于ANN 估计器和XU 估计器估算α、k 参数（αANN、kANN、αXU、kXU）矩阵。构建零差K 参数图像以及各参数PAX图像，利用成像结果对凝固区进行定量评估。

具体成像流程如图2 所示。先对超声背散射信号进行噪声辅助相关预处理，用零值代替无回声区域的噪声信号，然后利用希尔伯特变换进行包络检测。对包络信号进行对数压缩，可以得到B 超图像。利用滑动窗口法对未压缩的包络信号估算以针尖为中心3 cm×3 cm 感兴趣区内的αANN、kANN、αXU、kXU参数，将估算的参数矩阵进行数字扫描变换和颜色映射即可得到对应的参数图像。最后对参数矩阵每一个列向量、行向量分别进行4 阶PAX，可以得到近似为椭圆的PAX 图像

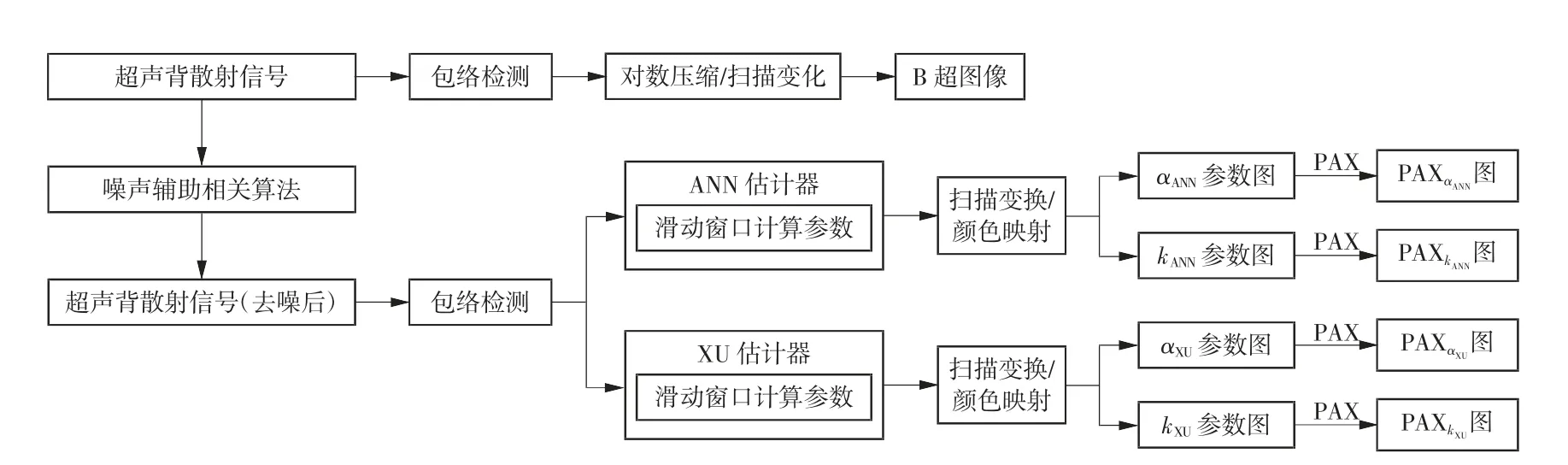
图2 超声成像流程

滑动窗口法是利用方形窗口以固定的窗口重叠率为步长在包络信号中滑动，计算当前窗口内的零差K 参数后将参数值赋给窗口中心像素。在估算参数时，使用小窗口可以提高图像的分辨力，对衰减的灵敏度较低；使用大窗口可以提高图像的平滑度，避免参数高估。滑动窗口的大小取决于换能器脉冲长度的倍数。Zhou 等[31]研究表明，滑动窗口≥5 倍换能器脉冲长度时，基于XU 法计算的α 参数与散射体浓度才开始呈线性相关，但k 参数的相关性研究未涉及。因此，为了限制滑动窗口大小对结果对比的影响，本文均采用5 倍换能器脉冲长度大小的滑动窗口进行αANN、kANN、αXU、kXU参数估计，窗口重叠率设置为50%。

1.4 评价指标

利用ROC 曲线对2 种估计器估算的参数成像监测凝固区的性能进行评估。以消融针针尖位置为中心，在B 超图、PAX 图中选取3 cm×3 cm 大小的感兴趣区。调整感兴趣区的大小，使其与组织切片图二值化处理得到的金标图具有相同的像素大小，然后进行归一化处理，使参数值的范围在0～1 之间。对比感兴趣区与二值化金标图，在0～1 阈值范围内，预测每一个像素，通过混淆矩阵绘制ROC 曲线。取距离坐标系左上角欧氏距离最小的点作为最佳阈值点，计算最佳阈值时区分凝固区与正常组织的准确率（accuracy，ACC）、敏感度（sensitivity，SEN）、特异性（specificity，SPE）、阳性预测率（positive predictive value，PPV）、阴性预测率（negative predictive value，NPV）。计算ROC 曲线的AUC，AUC 值越大，分类性能越好。利用Kruskal-Wallis 非参数检验对的AUC 值做显著性差异分析。

为了进一步评估ANN 估计器与XU 估计器监测凝固区的准确性，计算各参数PAX 图与金标图之间的Dice 系数和Jaccard 系数。Dice 系数和Jaccard系数表征整幅图像之间的相似性对比，系数越高，PAX 图评估凝固区的准确性越高。利用Tukey 检验分别分析参数αANN、kANN、αXU和kXUPAX 图之间Dice系数和Jaccard 系数的显著性差异。

绘制ROC 曲线和计算Dice 系数、Jaccard 系数通过MATLAB R2019a 软件实现，显著性差异分析通过SPSS 26.0（美国IBM 公司）软件实现。

2 实验结果

图3 为离体猪肝消融实验结束帧的B 超图、αANN参数图、kANN参数图、αXU参数图、kXU参数图。细胞坏死和热诱导的气泡会导致凝固区背散射信号的振幅明显大于正常组织。在B 超图像中，凝固区表现为高回声，正常组织表现为低回声。在参数图像中，参数被映射在0～1 之间，由蓝色到红色色阶表示参数值的递增，凝固区的参数值高于正常组织区域。随着消融持续时间的增加，气泡消散，每个分辨力单元内散射子的个数也会随之减少。

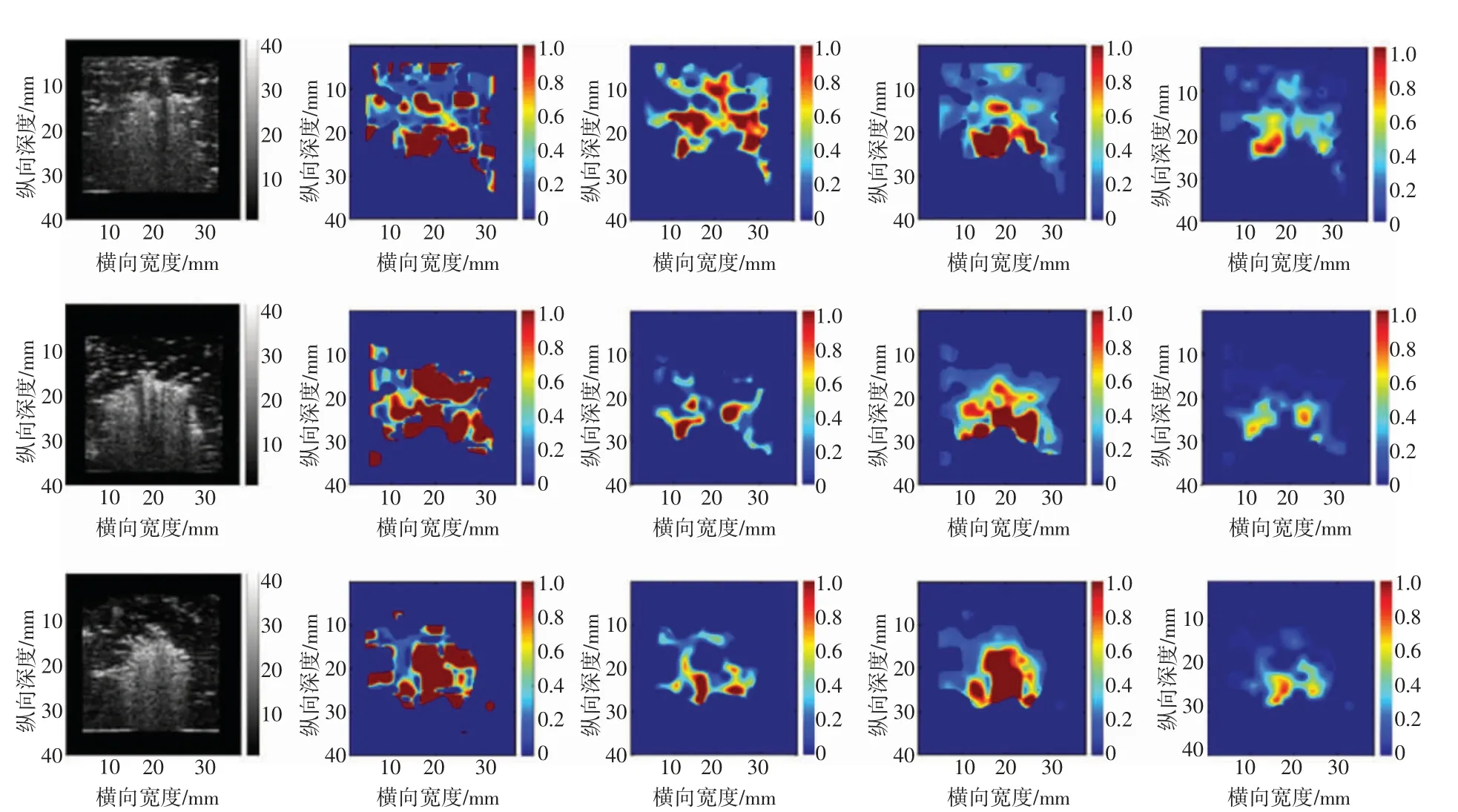
图3 离体猪肝消融实验结束帧的成像结果图

图4 为微波热消融离体猪肝实验后立即处理得到的组织切片图、金标图以及基于αANN、kANN、αXU、kXU参数的PAX 图。在组织切片中，肉眼可见的淡白色区域即为热消融产生的组织凝固坏死区域，边界用黄色轮廓线表示。ANN 估计器与XU 估计器估算参数进行PAX 得到的图像都能对凝固区的范围进行表征。大量实验发现以-6 dB 为阈值可以较好地表征凝固区范围[13，18，28]，因此在图中-6 dB 以内的区域被视为凝固区，以外的区域被视为正常组织，凝固区边界以黑色轮廓线表示。

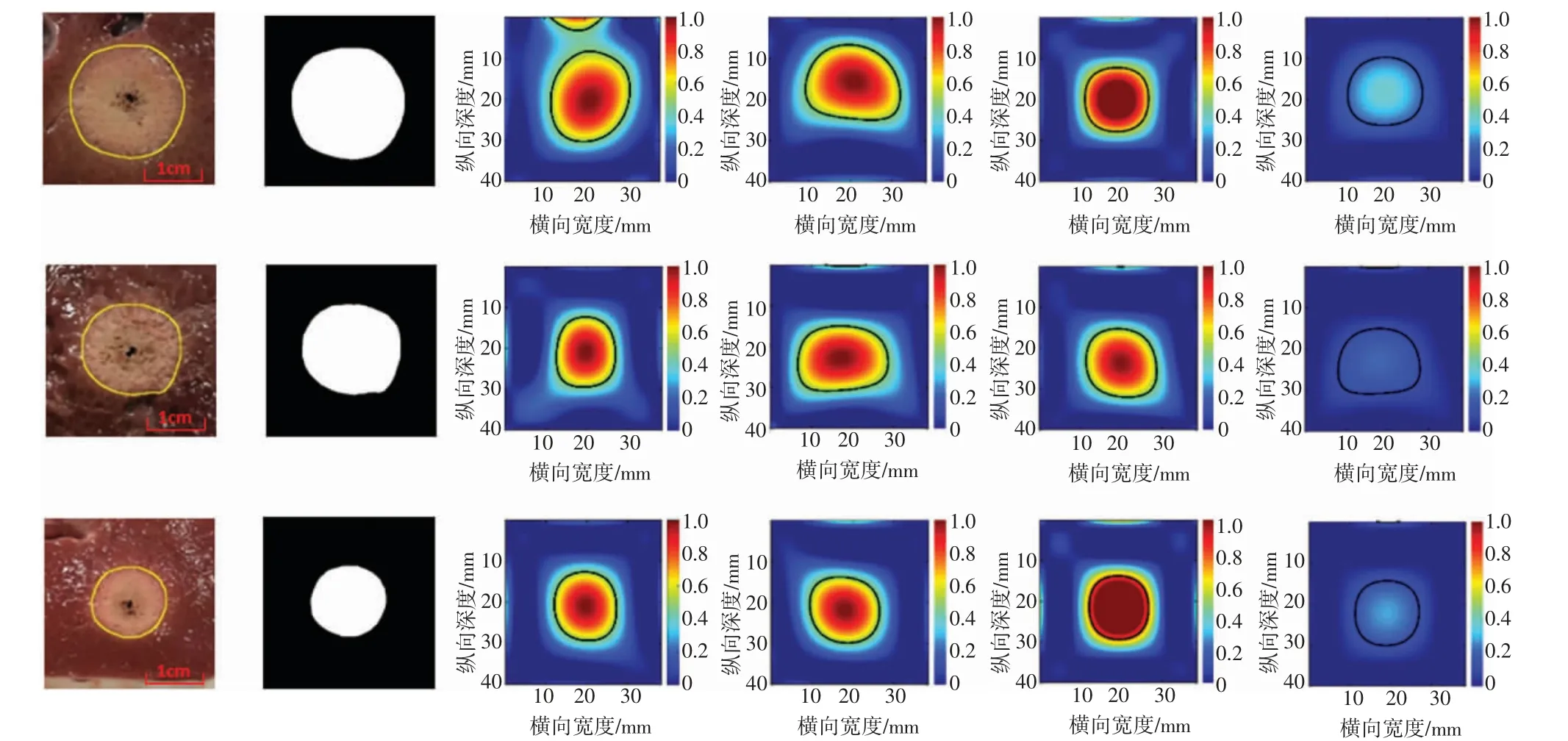
图4 离体猪肝消融实验后处理得到的组织切片图、金标图和各参数PAX 图

图5 为与图4 相对应的各参数PAX 成像监测凝固区的ROC 曲线。当消融功率与持续时间为60 W 3 min 时，αANN、kANN、αXU、kXU的AUC 值分别为0.941、0.890、0.997、0.985；当消融功率与持续时间为70 W 2 min 时，αANN、kANN、αXU、kXU的AUC 值分别为0.990、0.954、0.984、0.970；当消融功率与持续时间为80 W 1 min 时，AUC 值分别为0.986、0.972、0.984、0.966。从图5 可以看出，各参数PAX 图像的AUC 值均高于同一消融功率、持续时间下B 超图像的AUC 值。

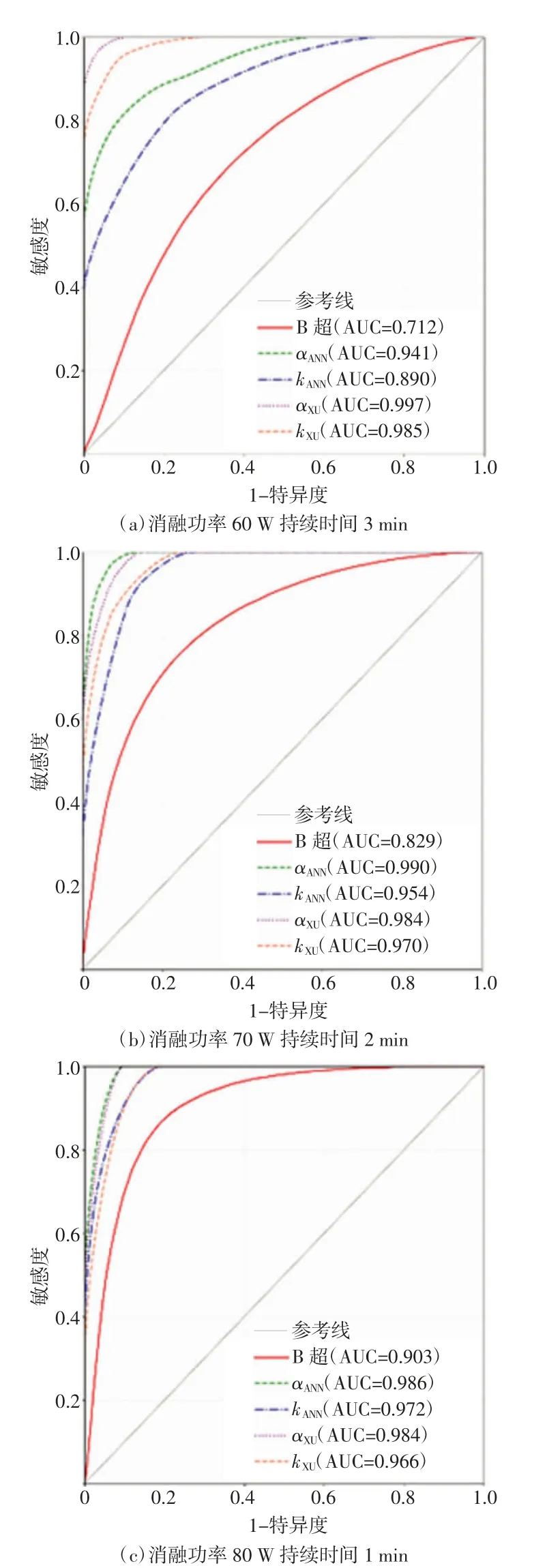
图5 B 超成像、各参数PAX 成像监测凝固区的ROC 曲线

表1 计算了不同消融功率、持续时间条件下4组参数PAX 图像AUC 值的中位数、上四分位数Q3、下四分位数Q1、四分位距IQR（Q3-Q1）。α 参数AUC 值的中位数总体比k 参数的高，IQR 总体比k参数的低。的AUC 值中位数在80 W 1 min 时最高，分别为0.985、0.910、0.965。的中位数在60 W 3 min 时最高，为0.979，但仅比80 W 1 min 时的AUC 值高0.002；和AUC 值的IQR 在80 W 1 min 时最低，AUC 值的IQR 在60 W 3 min 时最低，与80 W 1 min时仅差0.003。

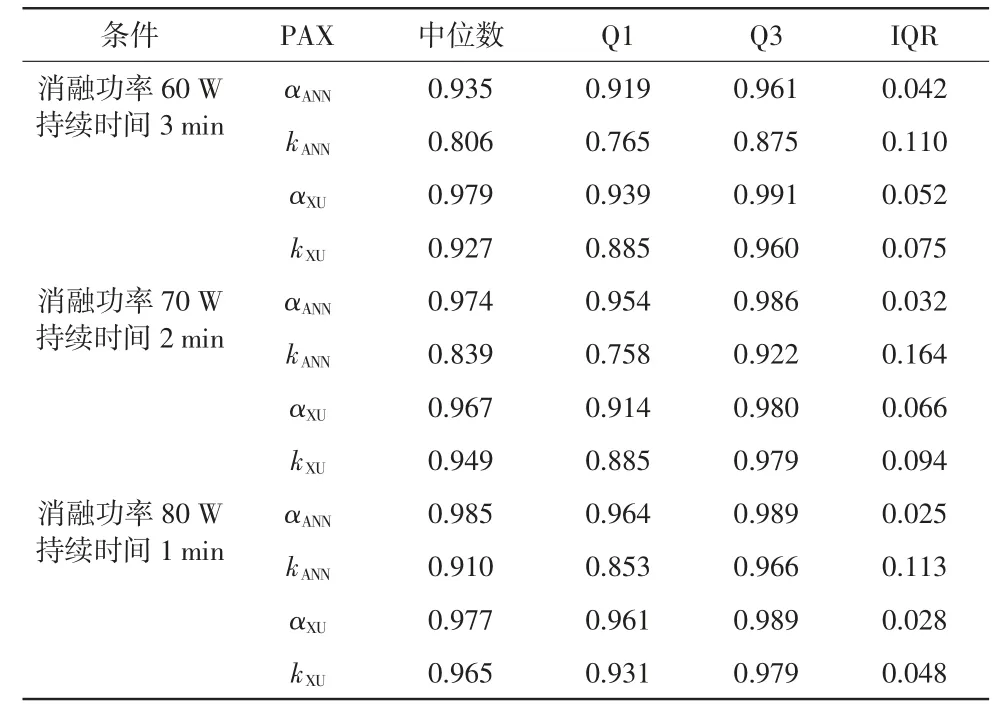
表1 不同消融功率、持续时间条件下各参数PAX 图像AUC 值的中位数、Q1、Q3 和IQR

表2 给出了B 超成像、各参数PAX 成像ROC曲线最佳阈值点处的指标。在不同功率、持续时间下，参数PAX 成像的指标均高于B 超成像的指标。各参数的ACC、SEN、SPE、NPV 均在80 W 1 min 时最高。除的PPV 在70 W 2 min 时最高外，其他参数的PPV 均在60 W 3 min 时最高。在60 W 3 min 时，的ACC、SEN、SPE、PPV、NPV 最高；在70 W 2 min 时的ACC、SEN、SPE、PPV、NPV 最高；在80 W 1 min 时的ACC、SPE、PPV 最高的SEN、NPV 最高，两参数指标仅相差1%左右。除在80 W 1 min 时SEN、NPV 的标准差高于外，其他组别各指标的标准差均低于其他参数。

表2 B 超成像、各参数PAX 成像ROC 曲线最佳阈值点处的指标统计结果（±s） 单位：%

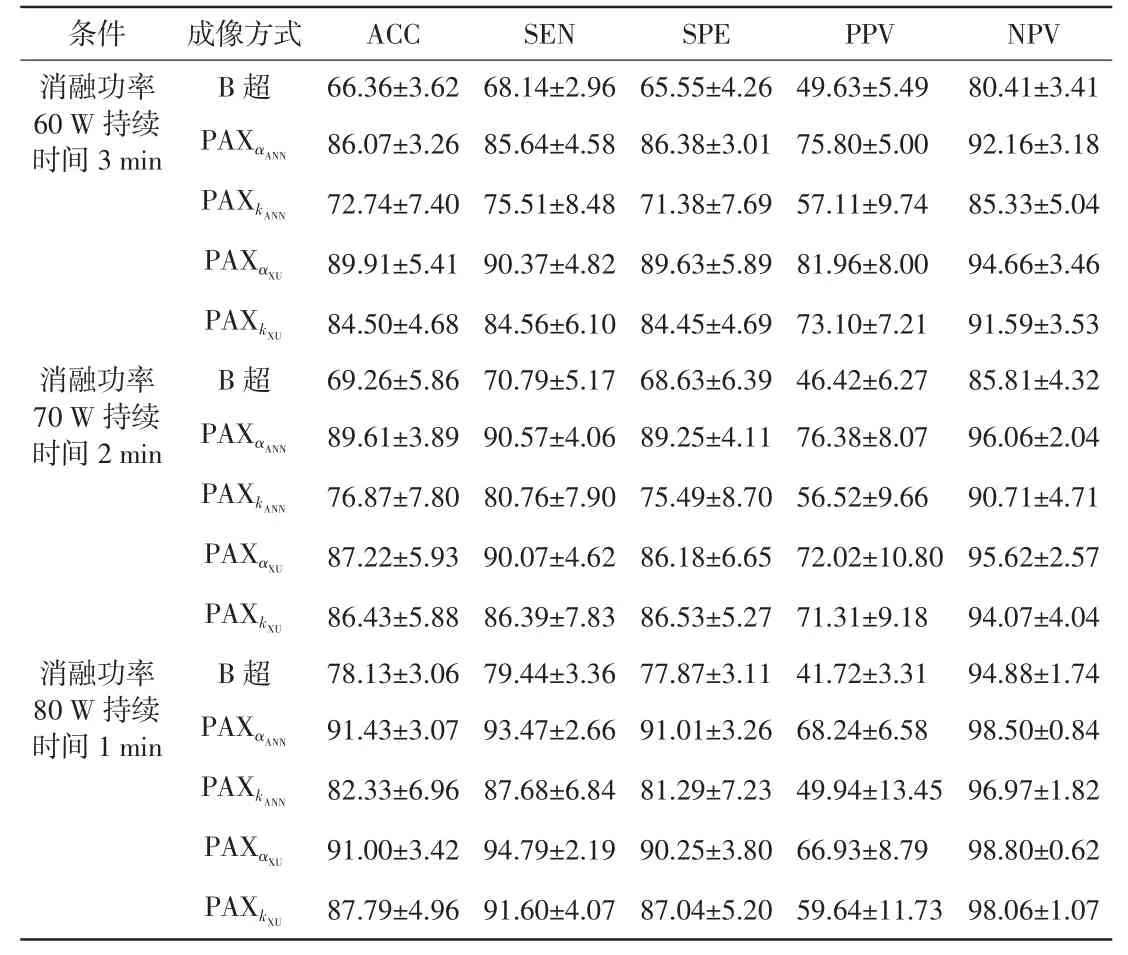
表2 B 超成像、各参数PAX 成像ROC 曲线最佳阈值点处的指标统计结果（±s） 单位：%

图6 比较了PAX 图像与金标准计算的Dice 系数、Jaccard 系数。PAXα计算的系数值总体比PAXk计算的系数值高，并且Dice 系数高于Jaccard 系数。统计分析结果表明，在60 W 3 min、70 W 2 min、80 W 1 min 时与的Jaccard 系数差异均有统计学意义（P<0.05），与的Jaccard 系数之间差异均有统计学意义（P<0.001）；与的Dice 系数在60 W 3 min、70 W 2 min 时差异均有统计学意义（P<0.05），在80 W 1 min 时差异有高度统计学意义（P<0.001）；与的Dice 系数仅在60 W 3 min 时差异有统计学意义（P<0.05）。在不同消融功率、持续时间条件下，PAXα之间的对比差异均无统计学意义（P＞0.05）。综上表明，与凝固区的相似度最低；基于ANN 估计器与XU 估计器计算得到的PAXα图像与凝固区的相似度水平一致，但ANN 估计器计算的标准差更低一些。

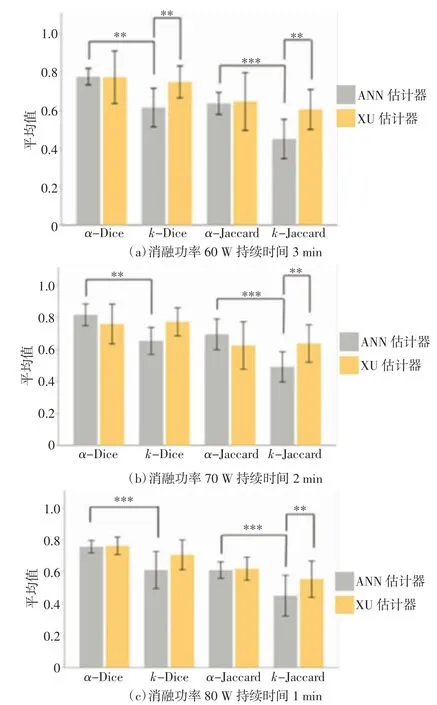
图6 PAX 图像与金标准之间Dice 系数、Jaccard 系数比较（±s）

3 讨论

本文基于ANN 估计器估算零差K 分布的α、k参数，将其应用到评估微波热消融凝固区中。利用离体猪肝采集的超声背散射信号，对比了ANN 估计器与XU 估计器评估凝固区的性能和准确性。

ANN 由输入层、一个或多个隐藏层和输出层构成，可以为特征和目标之间的复杂功能关系构建非线性预测模型[30]。先前的研究已经证实，相对于使用R、S、K 3 个特征参数或X、U 2 个特征参数的ANN 估计器，结合RSK 与XU 估计器使用5 个特征参数组合的ANN 估计器性能更好[29]。ANN 估计器的能力体现在学习和函数逼近方面。因此，在评估性能保持一致的前提下，ANN 估计器比RSK 估计器和XU 估计器更加灵活，并且计算速度更快。从图3～5 可以看出，基于ANN 估计器的零差K参数成像可以作为一种表征微波热消融凝固区的方法。

滑动窗口技术是构建超声参数图像的常用方法。使用不同的窗口大小会影响参数图像的分辨力和参数估计的稳定性（即参数图像的平滑度）[22]。如果为了获得良好的图像分辨力而选择相对较小的窗口，参数估计会因为窗口内包含的样本量较少而变得不准确[32]，这与先前的研究一致，即窗口内包含的样本量越多，参数估计的均方根误差越低[29]。综上，窗口大小的选择是图像分辨力和平滑度之间权衡的结果。在超声参数成像中，滑动窗口的大小可以设置为实际使用的超声换能器脉冲长度的倍数，Zhou 等[31]通过体模仿真实验得出：当窗口大小增加到超声换能器脉冲长度的5 倍或更高时，基于XU 估计器计算的α 参数才随散射体浓度的增加呈线性变化。因此，以5 倍换能器脉冲长度作为滑动窗口的大小可被视为实现基于XU 估计器的α 参数成像的最低要求。但目前还没有研究涉及到基于XU 估计器k 参数成像和基于ANN 估计器参数成像的窗口选择。在本文中，为了保持参数估计的一致性，ANN 估计器和XU 估计器的窗口大小都设置为换能器脉冲长度的5 倍。

结合表1 和图6 可以得出，无论是基于ANN 估计器还是基于XU 估计器，α 参数对凝固区的监测效果都要优于k 参数。统计学分析结果表明，在不同功率、持续时间下，AUC 值、Dice 系数、Jaccard 系数在基于ANN 估计器和XU 估计器计算的PAXα图像之间差异均无统计学意义（P＞0.05）。这可能是由于PAX技术通过将参数范围拟合成近似为椭圆的区域，拉近了参数评估凝固区的结果。除此之外，PAX 技术还弥补了不同功率下原始参数评估效果的差异，使得评价指标在不同功率、持续时间下没有明显的对比。不过需要注意的是，α 参数在80 W 1 min 时的成像效果更好。

从图3 中可以看出，α 参数图在80 W 1 min 时明显包含了更多的散射体信息。气泡作为有效信息能增强消融区的可视化。气泡活动的剧烈程度发生改变进而会导致背散射信号的统计分布发生改变。在消融初期，热效应产生的气泡剧烈活动会导致散射体浓度增加，背散射信号的统计分布从前瑞利分布向瑞利分布转变；而随着消融时间的增加，凝固区逐渐形成，气泡开始消散，使散射体浓度减少，背散射信号的统计分布又转变为前瑞利分布[11]。因此，消融持续时间增加，气泡活动减弱，每个分辨力单元内有效散射体的个数减少，即α 参数值降低，参数图中包含的散射体信息减少。除了气泡对参数成像结果产生影响外，在消融后期，凝固区作为强反射区，导致声衰减，在凝固区下方超声波不能准确探测到更多的有效信息，产生更强的后方声影（B 超图像中更为明显）。所以α 参数图在80 W、1 min 时的成像效果最好，但其在60 W 3 min 时的成像结果仍能表征凝固区。

表2 结果显示，PPV 值低、NPV 值高，代表预测的消融区面积大于实际的消融区面积。PAXαANN在80 W 1 min 时的ACC 值最高，对应于先前研究中ANN 估计器在高散射体密度中参数估计表现更好的结论[33]。综合所有的结果，ANN 估计器与XU 估计器均在80 W 1 min 时表现最好。

本研究尚有不足之处：首先，本研究利用采集的离体猪肝数据进行监测，每个消融功率时间组的数据量较少（只有16 例），未来应补充更多的实验数据并考虑使用在体数据对算法进行验证；其次，本研究所使用的窗口大小固定为换能器脉冲长度的5 倍，未来应对基于ANN 估计器的零差K 参数成像最低窗口大小标准进行仿真研究。

4 结论

本文首次探究了利用ANN 估计器估算零差K参数评估微波热消融凝固区的可行性。通过离体猪肝采集的超声背散射信号成像，对比了ANN 估计器和XU 估计器在不同消融功率、持续时间条件下监测凝固区的性能和监测的准确性。统计结果表明，在不同消融功率、持续时间条件下，参数对凝固区的监测效果均优于k 参数。2 种估计器估算α 参数PAX成像的AUC 值、Dice 系数、Jaccard 系数差异无统计学意义（P>0.05）。研究表明，基于ANN 估计器的超声背散射零差K 参数成像可以用于监测微波热消融产生的凝固区。