磁环型准零刚度隔振系统动态特性
李占龙,张正,姜稳稳,刘琪,任志曌,王瑶,宋勇
(1.太原科技大学 机械工程学院,山西 太原 030024;2.吉林大学 机械与航空航天工程学院,吉林 长春 130022)
0 引言
通常具有负刚度的机构有轴向受压的欧拉杆机构[6-10],以及用线性的竖直弹簧和两根斜弹簧并联来实现[11-13]。Valeev等[14]提出了单独碟簧和环形结构组合而成的碟簧模型。任旭东[15]采用两个水平对称空气弹簧作为负刚度。徐道临等[16]将5个线性弹簧并联组合,设计了非线性低频隔振器。蓝双等[17]在新的结构设计中弃用了压缩弹簧,采用拉伸弹簧的准零刚度隔振器,与前者对比后发现拉伸式具有更宽的准零刚度区间以及结构上的优势。杜宁等[18]通过利用平行四边形的不稳定性来产生负动刚度。Liu等[19]设计了凸轮-滚子-非线性弹簧机构,并讨论了水平阻尼对系统隔离力激励和位移激励的能力的影响。张春辉等[20]通过在平衡位置设置一定预紧力的准零刚度隔冲器来提高平衡位置附近的鲁棒性。Dong等[21]展开磁力准零刚度隔振技术研究,开发了由螺旋结合构成的高静态低动态刚度的多维低频隔振器。文献[22-25]分别利用等效磁荷法建立矩形永磁铁和双环形永磁铁的磁力和刚度解析模型。Kim等[26]将准零刚度隔振器应用于超精密测量传感器,实现对低频微幅振动的有效控制,大幅提高传感器精度。
本文针对特种车辆的低频隔振问题,基于非接触多磁环负刚度机构(NCNS) 和气动人工肌肉 (PAM) 正刚度平台构建了一种磁环型准零刚度隔振系统,对其系统刚度机理、参数特性和隔振特性进行了理论建模研究,并搭建实验平台对其进行验证。研究结果为后期特种车辆低频隔振系统的工程应用与实验提供一定的理论依据。
1 磁环型准零刚度隔振系统结构
建立了一种磁环型准零刚度隔振系统,如图1所示。负刚度机构(NCNS)包括上、下两个外部固定磁环和中间的自由磁环,自由磁环安装在中轴上,中轴和正刚度机构连接,振动通过球铰平台传递给中心轴,中心轴带动内磁环在上、下磁环之间运动,由于磁力作用产生负刚度。正刚度机构是由气动人工肌肉结构(PAM)单元构造的空间6自由度Stewart平台,主要功能是静态支撑和抵消磁负刚度,以适应承载刚度并降低隔振系统的隔振频率。承载平台由球铰与中心轴连接,通过直线轴承,可有效适应偏载工况。实际工程中隔振系统配套有上、下连接机构,上端的球铰结构更拓宽了隔振系统的使用领域和使用寿命。
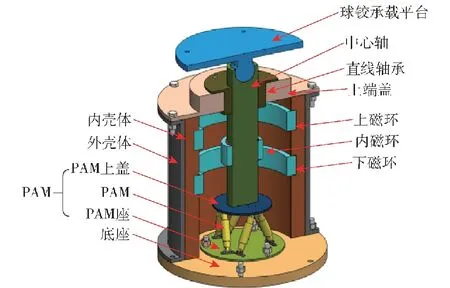
图1 磁环型准零刚度隔振系统Fig.1 Quasi-zero-stiffness vibration isolation system with magnetic rings
NCNS负刚度机构主要由同轴排列的上、下磁环和内磁环组成,如图2所示。将Onxnyn面与内磁环下表面中心点重合,内磁环垂向运动为zn轴,且向上为正。内磁环与上、下磁环沿轴向等距设置,距离为l;上、下磁环间距离为h;内磁环的内径、外径和厚度分别为di、Di、Ti,上、下磁环的内径、外径和厚度分别为do、Do、To,下角标i表示内磁环变量,下角标o表示上、下磁环变量,下角标oa指代上磁环变量,下角标ob指代下磁环变量。
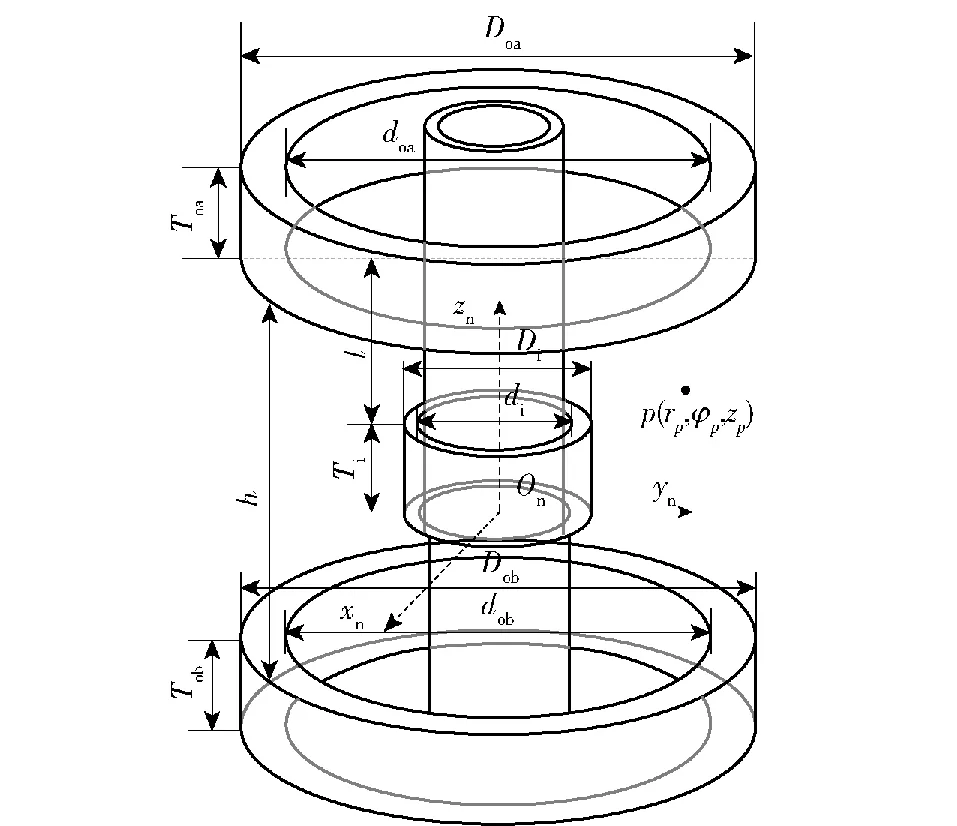
图2 负刚度机构坐标系Fig.2 Negative stiffness mechanism coordinate system
PAM正刚度平台为包含多环闭链结构的复杂多体系统,如图3所示。定义参考坐标系Oxyz,在上平台建立坐标系Ouxuyuzu,在下平台建立坐标系Odxdydzd,上、下平台铰点绕轴线旋转对称分布,6个PAM简化为线性阻尼弹簧单元lj(j=1,…,6)。其中,铰点a1与铰点a6关于坐标轴Ouxu对称,二者之间的夹角为2α,Oua1与坐标轴Ouxu之间的夹角α1;铰点b1与铰点b6关于坐标轴Odxd对称,二者之间的夹角为2β,Odb1与坐标轴Odxd之间的夹角β1。
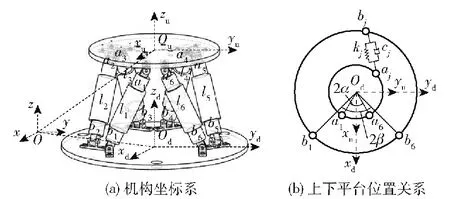
图3 正刚度机构坐标系Fig.3 Positive stiffness mechanism coordinate system
2 理论建模研究
2.1 负刚度机构理论建模
依据分子电流假说的理论得知,首先应当确定永磁体的磁矩,由体电流密度Jt和面电流密度Jm表示出,再由磁媒质中的安培定律得到体电流密度和面电流密度的表达式为
(1)
Jm=M×e
(2)
式中:M为沿轴向的磁化强度矢量;e为垂直磁体表面的单位矢量。内磁环强度矢量为Mi,外磁环强度矢量为Mo,其与剩余磁通密度Bi和Bo的关系分别为Mi=Bi/μ0,Mo=Bo/μ0,μ0=4π×10-7NA-2为真空磁导率。
在图2负刚度机构坐标系空间内取点p(rp,φp,zp),根据比尔-萨法尔定律可知,p点沿轴向磁化的环形永磁体产生的剩余磁通密度表示为
B(rp,φp,zp)=Br(rp,φp,zp)r+
Bφ(rp,φp,zp)φ+Bz(rp,φp,zp)z
(3)
(4)
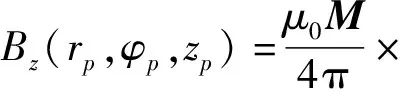
(5)
Bφ(rp,φp,zp)=0
(6)

(7)

内磁环承受的总磁力Ft由上磁环对其吸引力Foa和下磁环对其吸引力Fob叠加[27]:
Ft=Foa+Fob
(8)
(9)
(10)
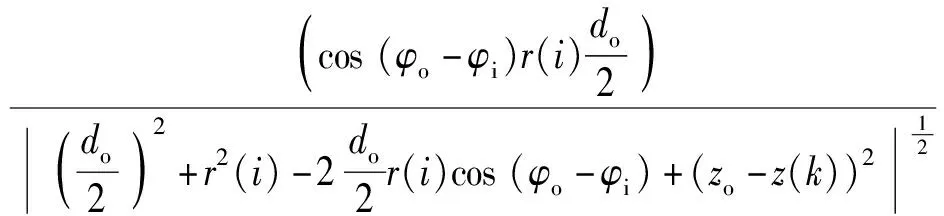
(11)
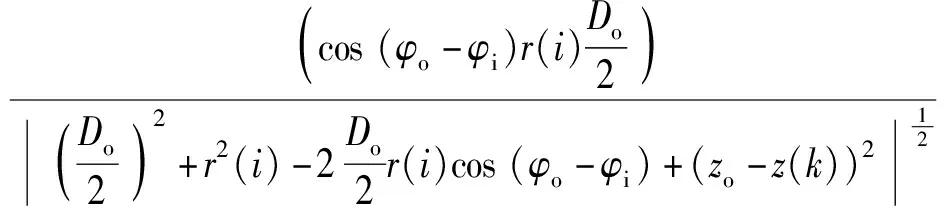
(12)
(13)
式中:zo、φo为外磁环内外圆柱表面上电流元的角度位置。
总磁力解析式如前所述,将内磁环轴向磁力对z(k)求1阶偏导数,得到NCNS非线性刚度解析式:
(14)
式中:
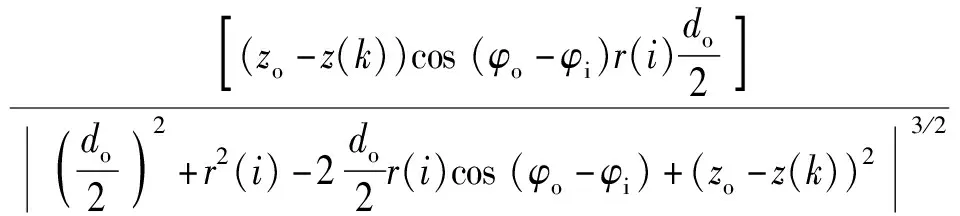
(15)
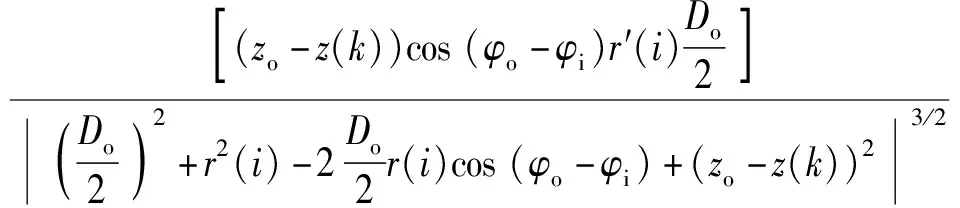
(16)
2.2 正刚度机构理论建模
如图3所示,上、下平台间距离为h0,在体坐标系Ouxuyuzu中,质心的位置矢量ruo、质心到第j个铰点的位置矢量aj分别为
(17)
在体坐标系Odxdydzd中,质心的位置矢量rdo、质心到第j个铰点的位置矢量bj分别为
(18)
经过坐标变换[28],可得位置矢量aj、bj到坐标系Oxyz中的表示为
(19)
式中:Ru、Rd分别表示坐标系Ouxuyuzu与坐标系Odxdydzd到坐标系Oxyz的转换矩阵,Ru、Rd的表达式为
(20)
式中:(αu,βu,γu)和(αd,βd,γd)分别表示坐标系Ouxuyuzu与坐标系Odxdydzd和坐标系Oxyz各轴的夹角。
由此可得,任意一个隔振单元lj上下两端之间的相对位移矢量ajbj在坐标系Oxyz的表达式为
AjBj=RuAj-RdBj
(21)
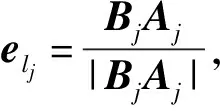

图4 单个PAM隔振单元刚度与阻尼的三向分解Fig.4 Three-direction stiffnessand damping decomposition of a PAM vibration isolation element
3个方向的刚度分量(kjx,kjy,kjz)和阻尼系数分量(cjx,cjy,cjz)表达式分别为
(22)
(23)
由此可以推出支撑平台3个方向的总刚度(kx,ky,kz)和总阻尼系数(cx,cy,cz)分别为
(24)
(25)
2.3 准零刚度隔振系统动力学建模
该隔振系统可以简化为如图5所示的非线性隔振模型,图中kn为双磁环负刚度,kk为支撑平台z轴方向正刚度,kk=kz,c为z轴方向阻尼系数,c=cz,M为被隔振物体质量,ZG为地面激励,ZM为被隔振物体位移响应。
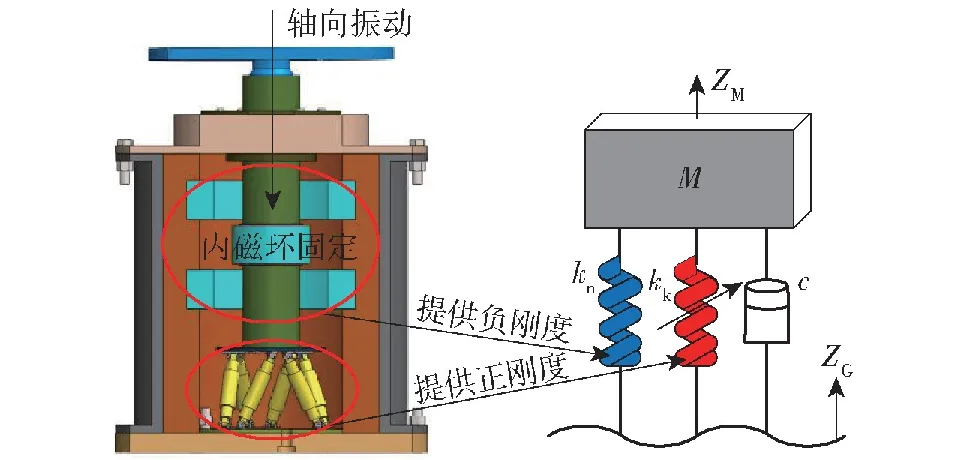
图5 单自由度非线性隔振系统动力学模型Fig.5 Dynamic model of single-degree-of-freedom nonlinear vibration isolation system
隔离物体的质量主要包括隔离物体和内磁环的质量(中心杆是由3D打印的轻质杆,可忽略其质量)。由于振动幅度限制在±40 mm范围内,支撑平台z轴方向正刚度kk近似呈线性[29]。由此系统的动力学方程可以表示为
(26)
该准零刚度隔振系统位移传递率为
(27)
3 刚度特性研究
3.1 负刚度特性研究
为掌握负刚度机构的刚度特性,分析负刚度机构的磁场耦合特性与力-位移特性,如图6所示。由图6可以发现,负刚度机构的主体磁路是一个轴对称回路结构,且磁力线呈均匀分布,除了在磁环边缘处有微弱的漏磁现象以外,大部分磁力线穿过磁环,磁对称性和保留性好。
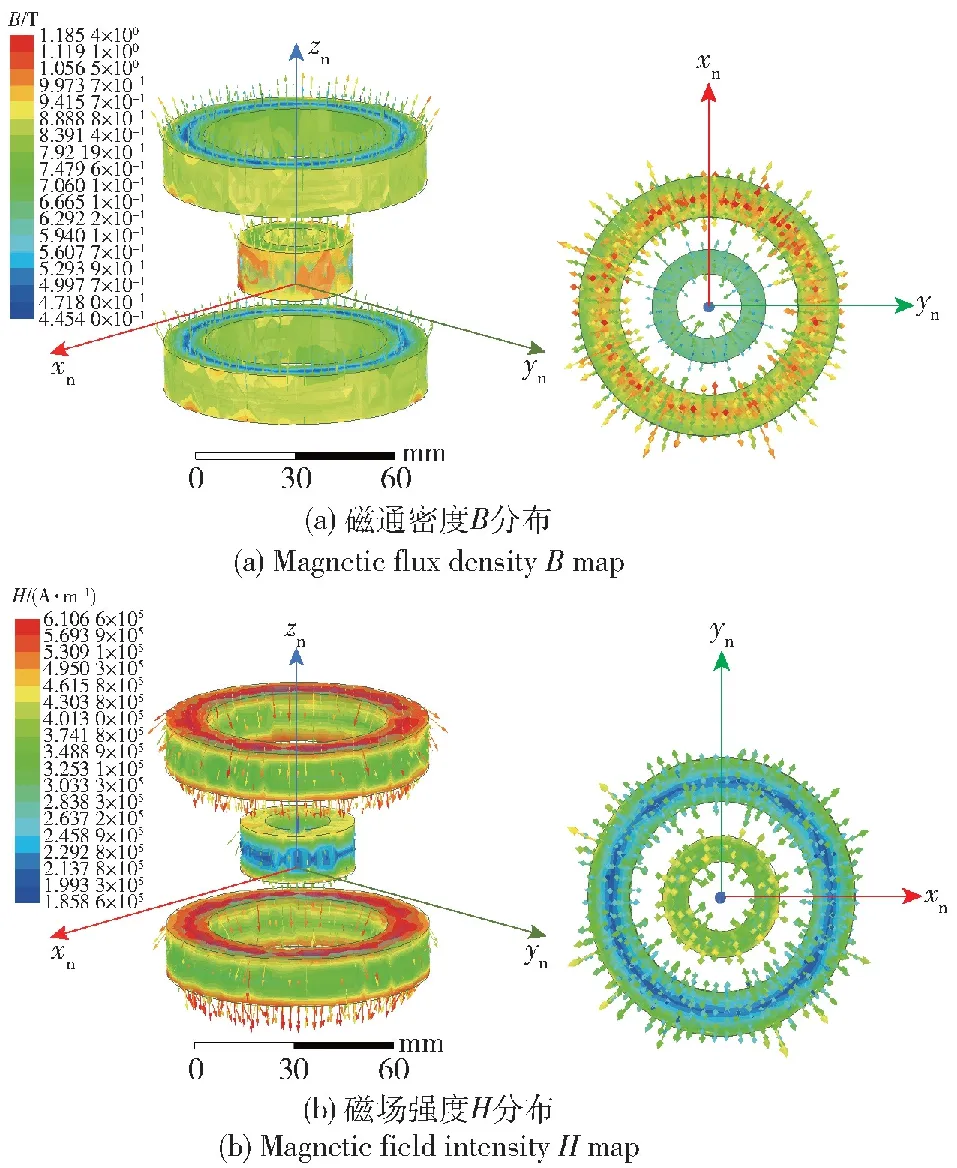
图6 负刚度机构计算模型Fig.6 Computation model of negative stiffness mechanism
同时,通过分析可以发现,随上、下磁环距离h增加,负刚度区间发生扩展,但负刚度峰值稳定不变。因此,可以在不改变负刚度行为特性的基础上,通过调节h扩展隔振系统的行程。同时,剩磁B的增加,负刚度机构的最大弹性力增大,其负刚度区间保持不变,与解析刚度式(15)一致。为了得到更宽的负刚度区间以及更大的承载能力,选取h=50 mm,B=1.25 T。最终得到的负刚度机构磁环参数如表1 所示。

表1 环形永磁体的参数Table 1 Parameters of permanent magnet rings
为验证负刚度模型的准确性,搭建了负刚度实验台,如图7所示。通过实验获得负刚度机构的力-位移特性曲线,与计算模型数据对比如图8所示。计算模型与实验数据基本吻合,二者校正决定系数R2值为0.977,验证了负刚度模型的可靠性。

图7 负刚度实验台Fig.7 Negative stiffness experimental bench
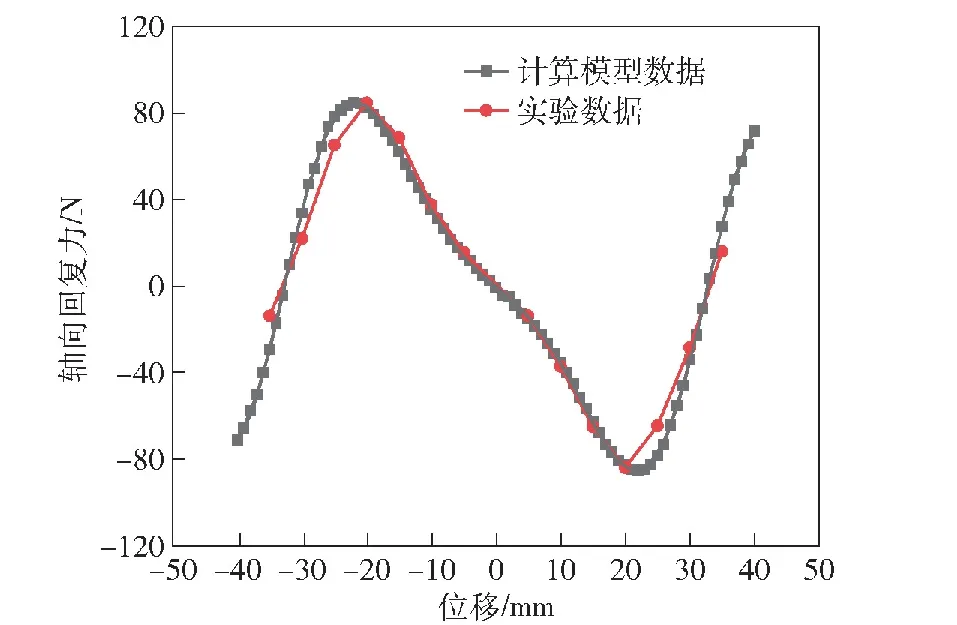
图8 负刚度计算模型与实验数据曲线Fig.8 Curves of negative stiffness computation model and experimental data
3.2 准零刚度特性研究
在负刚度模型中对内磁环等效输入不同的kk,导出的力-位移数据如图9所示,图中ΔZ=ZM-ZG。不难发现,该准零刚度隔振系统遵循刚度并联法则,同时,准零刚度区间在kk∈(4 000 N/m,6 000 N/m)时产生。为得到kk准确值,需得到系统力-位移的解析表达式。由于式(15)包含积分,其结构形式复杂,通过多项式拟合负刚度力-位移曲线获得,如图10所示,拟合R2值为0.97,拟合精度良好。

图9 负刚度模型在不同kk下的力-位移曲线Fig.9 Force-displacement curves of negative stiffness model under different kk

图10 负刚度力-位移拟合曲线Fig.10 Fitted force-displacement curves of negative stiffness
当kk的值为5 285 N/m时(见图11),隔振系统在±5 mm振幅区间表现为准零刚度。基于刚度并联原理得到隔振系统力-位移解析表达式:
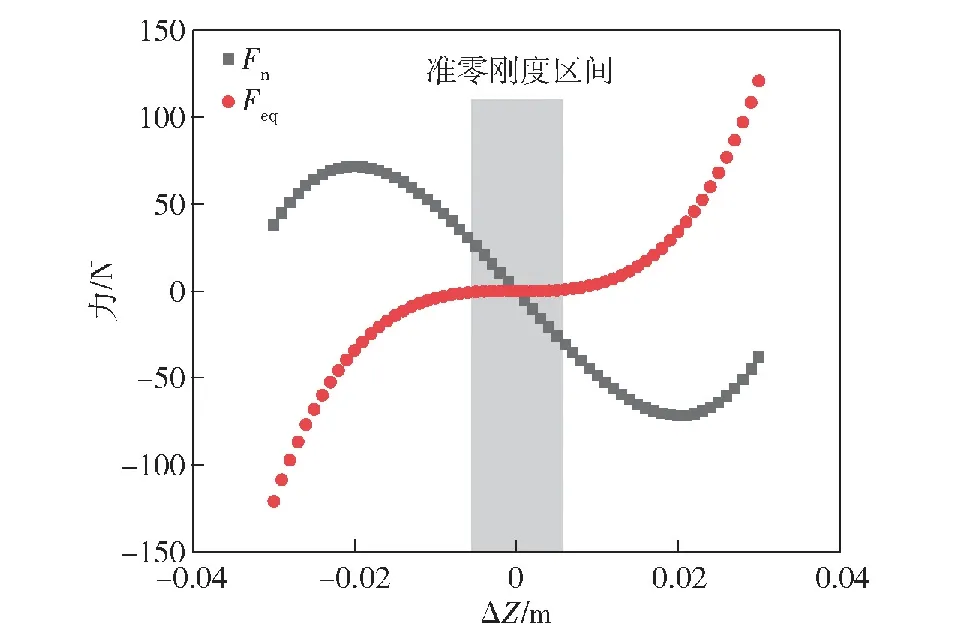
图11 准零刚度隔振系统与负刚度机构力-位移特性曲线Fig.11 Force-displacement characteristic curves of quasi-zero-stiffness vibration isolation system and negative stiffness mechanism
Feq=Fn+Fk=
f0+f1ΔZ+f2ΔZ2+f3ΔZ3+f4ΔZ4+f5ΔZ5+fkΔZ
(28)
式中:Feq为隔振系统刚度轴向回复力;Fk为正刚度轴向回复力;Fn为负刚度轴向回复力;f0=1.181×10-2N;f1=-5.284×103N/m;f2=-88.617 N/m2;f3=4.081×106N/m3;f4=7.322×104N/m4;f5=4.341×108N/m5;fk=5 285 N/m。
由式(29)得到隔振系统等效刚度表达式:
keq=kn+kk=
k0+k1ΔZ+k2ΔZ2+k3ΔZ3+k4ΔZ4+kk
(29)
式中:keq为隔振系统等效刚度;k0=-5.284×103N/m;k1=-1.77×102N/m2;k2=1.22×107N/m3;k3=2.93×105N/m4;k4=2.17×109N/m5。
4 隔振特性研究
准零刚度隔振系统非线性动力学方程如式(26)所示,为使后期迭代求解更精确,该非线性动力学方程可转换为
(30)

该非线性动力学方程可以通过HBM求解。假设外部激励和响应为谐波:
(31)
式中:H是外部激励的振幅;ω是频率;A和B是对应谐波分量的振幅;R0是偏差项。
式(31)代入到式(30)中,得
M(-Bω2cos (ωt)-Aω2sin (ωt))+
c(Aωcos (ωt)-Bωsin (ωt))+
kc(Asin (ωt)+Bcos (ωt)+R0)+
k1(Asin (ωt)+Bcos (ωt)+R0)2+
k2(Asin (ωt)+Bcos (ωt)+R0)3+
k3(Asin (ωt)+Bcos (ωt)+R0)4+
k4(Asin (ωt)+Bcos (ωt)+R0)5=MHω2sin (ωt)
(32)
式中:kc=k0+kk。
对式(32)进行三角函数约化并略去高次谐波项,得到一组非线性代数方程为
(33)
(34)
(35)
对于给定的参数,非线性代数方程组可以通过牛顿-拉夫森迭代算法进行数值求解。为了评估隔振系统的隔振性能,根据式(27),其位移传递率可以写成
(36)
图12(a)、图12(b)、图12(c)分别为不同激励幅值H、不同质量块M和不同阻尼c对隔振系统位移传递率的影响。随着激励幅值H和质量M增加或是阻尼c减少,从传递率曲线中能明显观察到解的跳跃现象,这是由于代数方程式(34) ~式(36)存在非线性项,激励幅值H和质量M的值相对较大或是阻尼c的值相对较小时诱发了系统的非线性行为。值得注意的是,曲线出现了向下跳跃现象,表明隔振系统是一个硬化系统。同时,随着激励幅值H增加,隔振系统的向下跳跃频率和共振峰值均增大;随着质量M增加,隔振系统的向下跳跃频率降低,共振峰值增大;阻尼c的增加使得向下跳跃的频率逐渐增大,共振峰值逐渐减少。
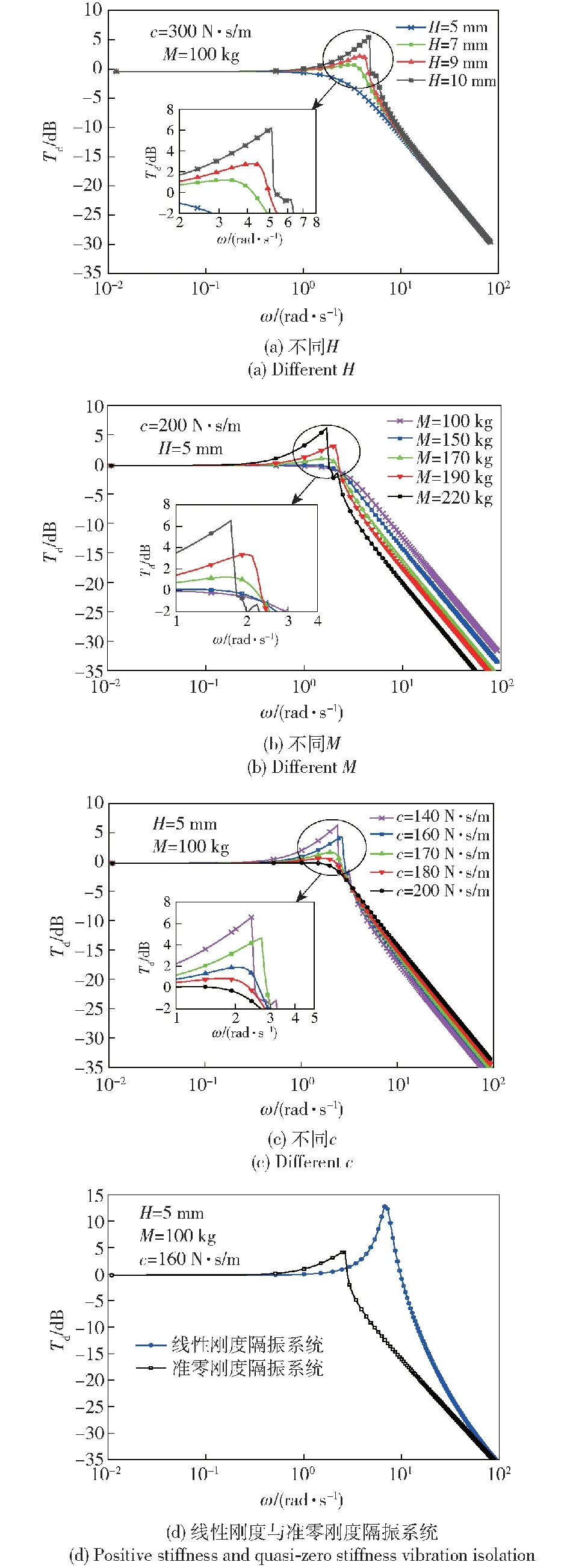
图12 不同参数下准零刚度隔振系统的位移传递率Fig.12 Displacement transmissibility of quasi-zero-stiffness vibration isolation system under different parameters
图12(d)展现了准零刚度隔振系统与线性系统(去除负刚度,只保留正刚度的系统)的传递率曲线对比图。由图12(d)可以看出:准零刚度隔振系统向下跳跃频率为2.71 rad/s,对应峰值为4.6 dB,起始隔振频率大约为2.81 rad/s;线性系统固有频率为7.21 rad/s,对应峰值为13.4 dB,起始隔振频率大约为10.01 rad/s。这说明准零刚度隔振系统可以将隔振频带向低频区拓宽71.9%,共振峰值降低了65.7%,具有更宽的隔振频带和更大的振动衰减率。在高频频带范围内,准零刚度隔振系统的振动响应收敛于线性参考系统。
5 实验研究
依据3.2节中的设计参数,选用PLA材料通过3D打印和定制磁环搭建出准零刚度隔振系统。上、下磁环和内磁环为z轴方向充磁,材料为钕铁硼NdFeB,具体参数见表1。配备扬州英迈克测试技术有限公司生产制造的YMC9200数字信号发生器、YMC结构模态激振器、YMCLA-200系列功率放大器和武汉优泰电子技术有限公司生产制造的UTeKL动态信号采集分析系统。为与仿真工况一致,将激励振幅限制在±5 mm之间,实验装置示意图如图13所示。

图13 实验方案示意图Fig.13 Schematic diagram of experimental scheme
准零刚度隔振系统与线性隔振系统实验结果如图14所示。由图14可知,准零刚度隔振系统对比线性系统能有效降低加速度和速度的响应幅值,稳态区间下位移响应幅值下降了75%,加速度响应幅值下降了80%,隔振效果显著。

图14 准零刚度隔振系统与线性隔振系统对比Fig.14 Comparison between quasi-zero stiffness vibration isolation system and linear vibration isolation system
6 结论
本研究针对特种车辆低频振动问题,构建基于NCNS负刚度机构和PAM正刚度平台的新型磁环式准零刚度隔振系统,对其进行了动态特性研究,并开展了相应的验证实验。得出主要结论如下:
1)负刚度机构能实现良好的负刚度,并于通过调节上下磁环距离h和剩磁值B进行负刚度区间及承载力大小的调节,以应对不同载荷条件。
2)隔振系统具有典型的非线性静态大刚度-动态小刚度特性。与线性系统相比,新型磁环式准零刚度隔振系统的隔振频带向低频区拓宽71.9%,共振峰值降低65.7%,稳态区间下位移响应幅值下降75%,加速度响应幅值下降80%,动态隔振特性优异。
3)下一步研究将考虑基于动态多目标优化的隔振系统参数匹配策略,以及工程应用与实验。

