基于余弦-指数非线性混沌映射的射频隐身抗分选信号设计技术
贾金伟,韩壮志,刘利民,解辉
(陆军工程大学石家庄校区 电子与光学工程系,河北 石家庄 050003)
0 引言
现代雷达面临干扰、反辐射攻击等严重电子对抗威胁[1]。雷达射频隐身技术能够降低雷达信号及其参数被电子侦察系统截获和识别的概率,提高雷达电子防御能力[2-3]。通常,雷达告警接收机等宽带实时电子侦察设备的侦测过程可分为信号截获、分选和识别3个阶段。与之对应,雷达射频隐身[4]主要有抗截获[5-7]、抗分选[8]和抗识别3类手段。其中,抗分选就是使电子侦察系统无法从随机交错的脉冲流中分离出各个雷达脉冲序列,是对抗电子侦察系统的一个重要突破点[9]。从两个方面对信号分选技术进行梳理:
1)一方面,从对信号的分选处理流程来分析。信号分选主要分为预分选和主分选两个过程。预分选是通过脉冲的载波频率(Radio Frequency,RF)、脉冲宽度(Pulse Width,PW)、到达方向(Direction of Arrival,DOA)对脉冲进行分类,实现对高密度脉冲流的稀释。主分选是辐射源信号分选的核心,通常是通过对各个脉冲的到达时间(Time of Arrival,TOA)进行处理,进而得到电磁环境中各个辐射源的脉冲重复间隔(Pulse Repetition Interval,PRI)及其调制方式[10]。所以,要削弱电子侦察系统对信号的分选,首先要对抗基于TOA的主分选。
2)另一个方面,从对信号分选的研究方向来分析。雷达辐射源信号分选技术主要有3个研究方向:基于脉间调制特征的雷达辐射源分选、基于脉内调制特征的雷达辐射源分选和基于机器学习的雷达辐射源分选[11]。基于脉间调制特征的雷达辐射源分选主要是基于脉冲TOA对信号PRI进行分选。基于脉内调制特征的雷达辐射源分选主要是通过提取更稳定、更细微、参数交叠更少、区分度更高的脉内调制特征来解决信号分选问题。基于机器学习的雷达辐射源分选是利用机器学习在数据分析、分类及预测等领域的特长对信号进行分选。虽然在每一个研究方向都有一大批研究成果,但应用于雷达告警接收机等宽带实时电子侦察设备时均存在不同程度的不足。基于脉内调制特征的雷达辐射源分选需要提取脉内更加细致的特征,所以此类方法计算量普遍较大,且抗噪性表现较差,难以适应电磁环境的复杂变化。基于机器学习的雷达辐射源分选的不足是需要预先获取大量非合作辐射源信号样本进行训练集,在实际应用中有较大难度。同时机器学习中的信号分选模型需要经过较长时间的训练才能收敛,难以满足战场实时性要求。因此,宽带实时电子侦察设备仍以基于脉间调制特征的雷达辐射源分选方法为主,结合与业内信号分选工程实践领域专家讨论交流的成果,序列差值直方图(Sequential Difference Histogram,SDIF)算法及其改进算法是信号分选工程实践领域广泛使用的核心算法。所以,抗分选主要是对抗基于TOA的SDIF分选算法。
当前,抗分选研究主要聚焦于抗分选信号设计技术。主要包括干扰脉冲抗分选[12-15]、抖动PRI抗分选[14,16-17]和PRI优化抗分选[18-19]等方式。上述方法虽然取得了一定的效果,但信号在设计时没有以分选失效原理作为基础,制约了信号的设计效率。
本文研究PRI分选算法中经典SDIF算法的失效原理,并以此为基础,运用一种改进的一维混沌系统,设计射频隐身抗分选信号,并通过仿真验证信号的抗分选性能。。
1 抗分选信号设计原理
抗分选信号设计原理主要是通过对信号分选算法的研究,分析得出分选失效机理,进而为抗分选信号的设计提供理论支撑,提高信号抗分选设计的效率和成功率。
1.1 基于SDIF的分选算法
雷达信号源分选,又称雷达辐射源信号去交错,是指从随机交错的脉冲流中分离出各个雷达脉冲列的过程,本质是上是信号各个脉冲的参数匹配问题。在实际的工程领域内,最常用的是直方图分选方法。直方图分选方法是借鉴统计学原理对辐射源信号的PRI值进行估计。通过统计TOA的差值,形成TOA差值直方图,然后设置合适的分选门限和分选策略。工程上常用的改进算法主要有累计差值直方图(Cumulative Difference Histogram,CDIF)算法和SDIF算法两种。
从本质上讲,SDIF和CDIF算法都属于TOA差值直方图分选算法。两种分选算法都是按照一定的规则对脉冲的TOA差值进行统计,分析得出PRI估计值,然后根据PRI估计值进行脉冲序列搜索,将辐射源脉冲序列提取出来[20-21]。与传统的直方图分选算法相比,SDIF和CDIF算法大幅度降低了计算量,满足实时性的要求,可以对PRI固定、PRI参差和抖动的辐射源信号进行分选,在工程领域中得到了广泛应用[22-24]。
与CDIF算法相比,SDIF算法具有以下优点:一方面SDIF算法不累积不同级别的直方图统计值,只统计分析当前级别的直方图,同时取消了2倍PRI检测,减少了计算量、提高了处理速度;另一方面,SDIF算法对门限函数进行了优化改进,与子谐波检测相配合,避免了虚假检测的发生。因此,SDIF算法的应用更为广泛。SDIF信号分选算法流程如图1所示。

图1 SDIF信号分选算法Fig.1 SDIF signal sorting algorithm
由图1可知,SDIF分选算法主要包括对TOA差值直方图的分析和脉冲序列搜索两部分。TOA差值直方图分析主要是用来估计PRI值。运用直方图统计的方法将从1阶开始对逐级TOA差值次数进行统计。如果TOA差值统计次数存在超出检测门限的峰值,那么峰值对应的TOA差值除以TOA差值统计级数就是可能存在的PRI值。SDIF算法的门限函数为
Tthre(τ)=a(E-C)e-τ/kN
(1)
式中:τ表示PRI值;a是可调常数,一般由脉冲丢失率确定;E是脉冲总数;k是[0,1]内的常数;N是直方图统计的小区间个数。
在SDIF分选算法对信号的实际分选过程中,为避免截获接收机对脉冲TOA测量误差的影响,同时增强算法对抖动信号的分选性能,所以在SDIF及其改进的分选算法中,设置了信号PRI值T的容差ε,即PRI小盒。小盒的上、下限分别为
Tmax=T+ε
(2)
Tmin=T-ε
(3)
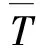
(4)
式中:xi为容差内单个Ti对应的脉冲数量;S为容差内邻近PRI值T1,T2,…,Tn对应的脉冲数量总和。
1.2 分选失效原理
1.2.1 1阶直方图的分选失效原理分析
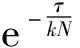
1.2.1.1 信号PRI值由1个增加为有限多个
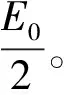
根据式(1),PRI的值τ=τ0时,算法的门限值为
Tthre(τ0)=a(E0-1)e-τ0/kN
(5)
PRI的值τ=τ1时,算法的门限值为
Tthre(τ1)=a(E0-1)e-τ1/kN
(6)
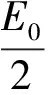
(7)
由于E0表示脉冲总数,通常有成千上万个,E0≫1。所以,式(7)简化为
(8)
所以,对式(8)取自然对数后,可得τ′为
τ′=kNln (2a)
(9)


τ′=kNln (na)
(10)
因此,当信号的PRI值增为有限个,SDIF算法无法分选出PRI小于临界值kNln(na)的信号脉冲。
1.2.1.2 信号PRI值服从区间分布
假设脉冲数量仍有E0,PRI值为区间分布,即τ∈[τmin,τmax]。因为在雷达领域需要统筹考虑发射信号的设计与回波信号的处理两个方面,所以雷达信号PRI值不会是完全的随机无序分布,通常采用多个PRI值贯序重复发射的方式。因此,在本节内以信号PRI值服从均匀分布进行讨论。对于区间内任一确定的τ,其脉冲数量E′为
(11)
式中:τmax和τmin为分布区间的最大值和最小值;z为区间分布内PRI值的最小间隔。PRI的值为τ′时,算法的门限计算公式如式(1)所示。
当Tthre(τ′)=E′时,
(12)
所以,式(12)简化为
(13)
因此,求解出分选失效的PRI临界值τ′为
(14)
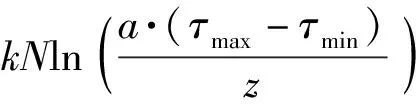
综上所述,在1阶直方图的分选失效原理分析中,若信号PRI值服从区间分布,在区间长度大于区间间隔的20倍时,区间内PRI值对应的脉冲数量均小于分选算法的门限值,SDIF算法分选失效。
1.2.2 多阶直方图的分选失效原理
SDIF分选算法在1阶直方图中存在多个过门限的PRI值时,需要统计2阶、3阶至高阶直方图,进而得出PRI估计值,所以同样需要对2阶至高阶直方图的分选失效原理进行分析。
门限函数如式(1),在2阶至多阶直方图中,只是直方图阶数C发生变化,与脉冲总数E相比,E≫C,所以门限公式近似无变化。因此,信号PRI值服从区间分布的时候,1.2.1节中1阶直方图对于SDIF算法分选失效原理的分析仍然适用。
通过第1.2节的分析讨论,当雷达信号PRI值服从长度为PRI最小间隔20倍以上的区间分布时,信号脉冲在各阶TOA差值直方图的累积量均小于分选算法门限,将导致分选算法失效。
1.3 关于抗分选信号设计原理的讨论
信号分选是指从随机交错的脉冲流中分离出各个辐射源脉冲列的过程,其本质是利用脉冲流中各脉冲之间的相关性,将属于同一个辐射源的脉冲序列相互匹配,进而实现信号分选。
根据第1.2节的分析,在雷达信号PRI值服从长度为PRI最小间隔20倍以上的区间分布时,降低了脉冲流中同一辐射源各脉冲之间的相关性,使得同一辐射源的各脉冲之间呈现弱相关性,进而导致信号脉冲在各阶TOA差值直方图的累积量均小于分选算法门限。
因此,为进一步减少脉冲序列之间的相关性,强化其随机性,基于前文失效机理,利用强随机性的混沌序列对信号PRI进行调制,提高雷达信号抗分选性能。
2 基于CE混沌映射的信号设计
2.1 混沌模型
混沌系统是一种存在确定表达式的非线性系统,表达式经过多次迭代,系统会表现出很强的随机性、初值敏感性和不可预测性。由系统产生的混沌信号在时域和频域分布上类似于噪声,具有较宽的频带和长期的不可预测性,主要分为一维混沌系统、二维混沌系统和高维混沌系统[25-30]。与随机系统不同的是,由于混沌映射表达式是确定的,所以混沌系统也是确定的。因此,混沌系统产生的混沌信号既具有类似于噪声的随机性又具有混沌的确定性。类似于噪声的随机性增强了信号的抗分选性能,所以在符合第1节抗分选信号设计原理的基础上,运用混沌系统对信号的PRI进行调制,信号的抗分选性能亦有所提升。
考虑到系统对序列生成的要求和工程实践中对混沌系统复杂度、运算量的限制,一维混沌系统由于其高效、快捷被广泛使用。典型的一维混沌映射有Logistic映射、Chebyshev映射、Cubic映射,各映射对应的表达式分别如式(15)~式(17)所示:
xn+1=rxn(1-xn),xn∈[0,1]
(15)
xn+1=cos (parccos (xn)),xn∈[-1,1]
(16)
(17)
式中:r为Logistic映射的控制系数,r∈[0,4],当r≥3.57时,系统处于混沌状态[31];p为Chebyshev映射的控制系数,当p≥2时,系统处于混沌状态[32];q为 Cubic映射的控制系数,当q≥2.3时,系统处于混沌状态[33]。3种映射处于混沌状态时,均表现出比较低的混沌状态,不利于抗分选信号的设计。为此,受到典型的Logistic映射启发,本文设计一种基于余弦-指数的一维非线性混沌映射,混沌映射主体是三角函数余弦函数,余弦函数内部包含πrxnexn(1+x)和π(exn+x3)两部分,第1部分πrxnexn(1+x)是产生混沌序列的主体,第2部分π(exn+x3)主要是通过指数项和高次项进一步增强第1部分所产生混沌序列的随机性和不可预测性,如式(18)所示:
(18)
引入cos函数的目的是为了将混沌映射的输出值控制在[-1,1]之间,这样可以将信号的PRI中心值与混沌映射的输出中心值0相对应,映射输出值1和-1可以对应任意的PRI变化范围极限。第2部分的指数项πexn消除了初始值不能为0的限制,使得混沌序列的产生更加灵活,且系统是否进入混沌状态不再受控制系数值的限制,能够更快地进入混沌状态,如图2所示。

图2 本文所提出的混沌映射分岔图和序列点图Fig.2 The chaotic mapping bifurcation diagram and sequence point diagram proposed in this paper
2.2 基于CE混沌映射的调制信号
根据第1节抗分选信号设计原理,当雷达信号PRI值服从长度为PRI最小间隔20倍以上的区间分布时,信号脉冲在各阶TOA差值直方图的累积量均小于分选算法门限,将导致分选算法失效。因此,信号设计原理为设计信号指明了PRI捷变需服从的区间长度,运用强随机性的混沌序列对信号PRI进行调制时,PRI捷变的区间长度至少大于区间最小间隔的20倍。
信号的PRI值T根据CE混沌映射产生的序列进行调制,调制函数如式(19)所示:
Tn=T0+xn·ΔT
(19)
式中:T0是信号PRI中心值;ΔT是信号PRI最大变化量。调制后的PRI值序列仍具有混沌序列的随机性,但如图3红色圈所示,混沌映射调制的PRI值序列存在多值窄间隔效应,即序列中存在多个相邻的脉冲PRI值之间间隔较小,导致相邻的脉冲落入同一个脉冲分选容限内。
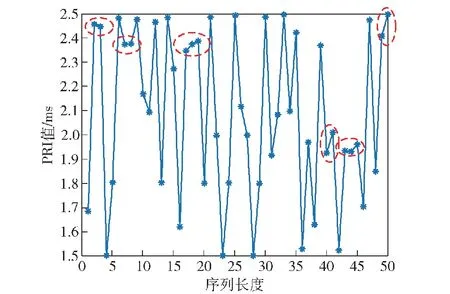
图3 PRI调制后的多值窄间隔效应图Fig.3 Plot of multi-valued narrow interval effect after PRI modulation
因此,在混沌序列对PRI值进行调制之前,需要对混沌序列的生成方法进行改进,以消除多值窄间隔效应。在混沌映射每生成一个序列值xn,首先要对xn及上一个值xn-1进行间隔判断,若间隔满足要求,则保留该值xn,将xn代入混沌映射表达式进行下一步的迭代产生xn+1,再判断xn+1与xn之间的间隔,依次类推;若间隔不满足要求,则舍弃xn,判断xn-1与由xn迭代产生的xn+1之间的间隔是否满足要求,若满足间隔要求,保留xn+1,若不满足间隔要求,则舍弃xn+1,比较xn-1与xn+2,直至得到满足要求的混沌序列值。同时,为了滤除部分集中在序列值边界的点,对满足间隔要求的序列点值增加了临界值判断步骤xn+Δx<1和xn-Δx>-1。具体的信号PRI序列生成流程如图4所示。
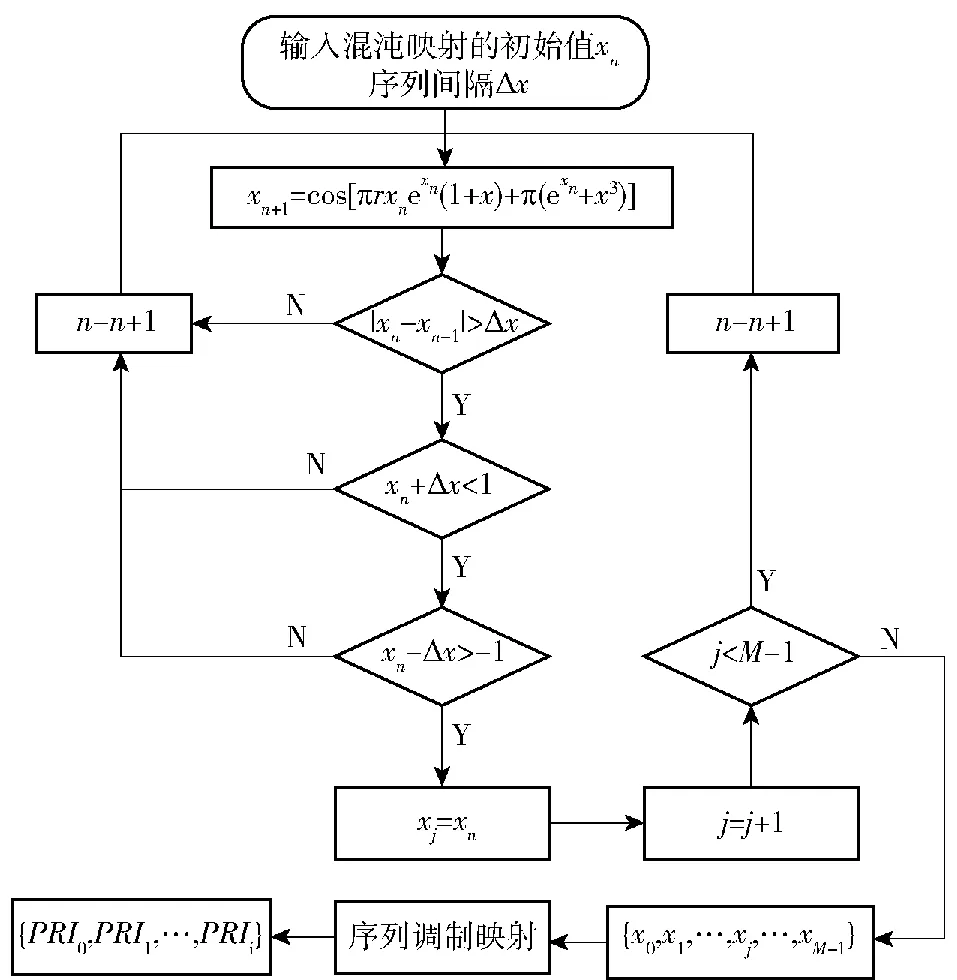
图4 PRI序列生成流程图Fig.4 Flow chart of PRI sequence generation
3 仿真验证
3.1 混沌序列的性能仿真
3.1.1 混沌映射性能分析
为了进一步说明本文所提出的CE混沌映射的优点,选用典型的一维混沌映射Logistic映射、Chebyshev映射、Cubic映射与本文所提映射对比,从混沌映射的分岔图、最大李雅普诺夫指数(LE)、近似熵、平衡性方面进行分析比较:
1)混沌映射的分岔现象是映射进入混沌状态的标志之一,通过描绘映射的分岔图可以直观地观察到映射的混沌区域和映射中的控制参数对混沌的影响。下面根据Logistic映射、Chebyshev映射、Cubic映射和本文所提映射4种映射的表达式绘制分岔图,如图5所示。
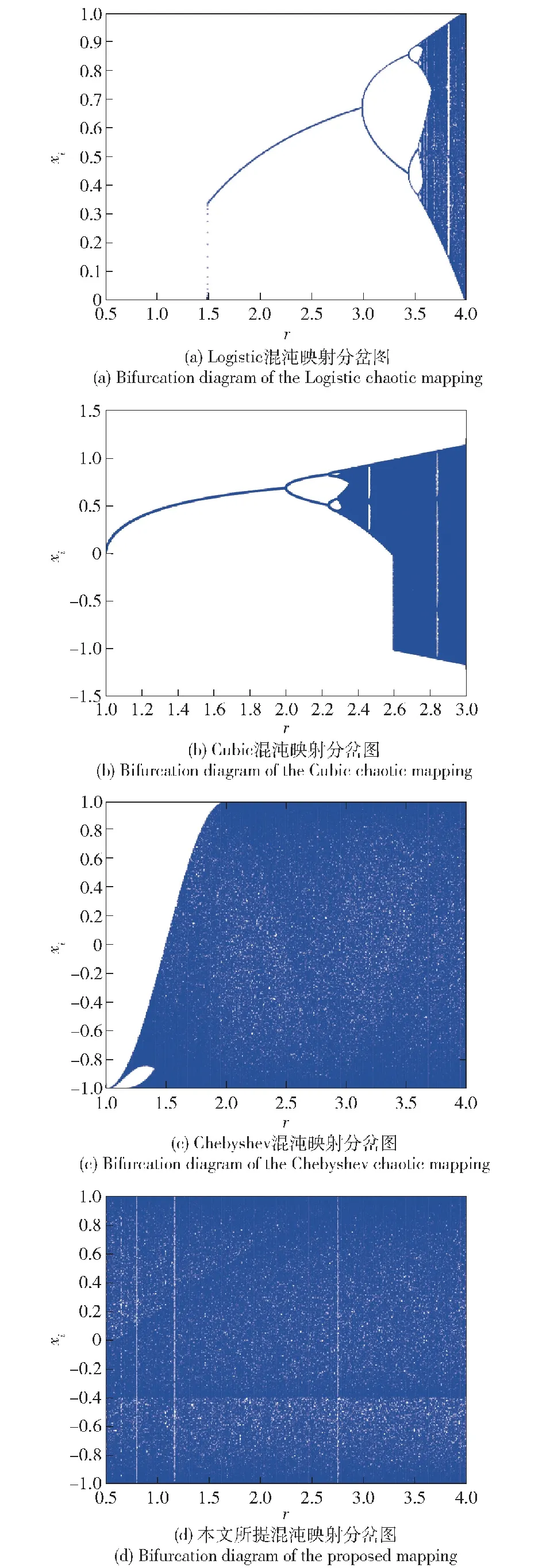
图5 4种混沌映射分岔图Fig.5 Bifurcation diagrams of four chaotic mappings
由图5所示:Logistic映射只有在分形系数r≥3.57时,系统才会进入混沌状态,当0≤r<3.57时,系统处于周期状态;Cubic映射在分形系数r≥2.3时,系统进入混沌状态,当0≤r<2.3时,系统处于周期状态;Chebyshev映射在分形系数r≥1.5时,系统进入混沌状态,当0≤r<1.5时,系统处于周期状态;本文所提出的CE混沌映射不受分形系数的影响,分岔图中的各点在图中分布更加均匀。
2)最大 LE是用来评估混沌序列的随机性,其定义如式(20)所示:
(20)
式中:f′(xi)表示混沌映射f(xi)=xn+1的1阶导数。当最大李雅普诺夫指数大于0时,表示系统处于混沌状态,其值越大表示系统产生的混沌序列随机性越强。下面绘制上述4种具有不同分形系数的混沌映射LE变化曲线,如图6所示。
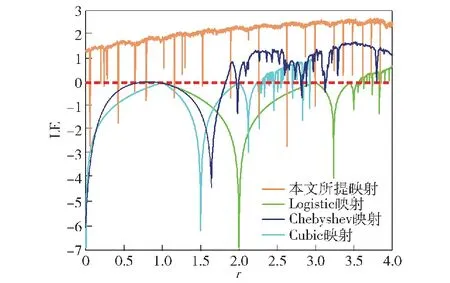
图6 不同混沌映射的LE对比Fig.6 Lyapunov index comparison diagram of different chaotic mappings
由图6可知,Logistic、Chebyshev以及Cubic 3种映射LE并不是一直大于0,表明了3种系统并不是一直处于混沌状态。以Logistic映射为例,只有当r≥3.57时,系统才处于混沌状态。本文所提出的混沌映射在分形系数变化区间[0,4]中,其LE除了个别点小于0,其他均大于0,避免了分形系数的限制。同时,LE大于另外3种一维混沌映射,表明本文所提的CE混沌映射生成的混沌序列比另外3种一维混沌映射生成的混沌序列具有更强的随机性。
3)近似熵主要是衡量由混沌映射生成混沌序列的复杂性。近似熵值越大代表序列具有更高的复杂性。在相同的仿真条件下计算上述4种映射的近似熵,其中分形系数取值从0.5到4.0以步长为0.5变化,序列长度设置为10 000。得到的结果如表2所示。由表中的计算结果可知,当系统没有进入混沌状态时,近似熵的值极小甚至为0。例如,当r=0.5和r=1.0时,Logistic、Chebyshev以及Cubic 3种映射的近似熵值在10-5或10-7数量级,Chebyshev映射在r=1.0时,近似熵值为0。而本文所提的混沌映射在分形系数变化区间内,均保持大于1的近似熵值,表明该映射产生的序列具有更高的复杂性。

表2 4种不同混沌映射的近似熵值随分形系数的变化Table 2 The approximate entropy of four different chaotic mappings varies with fractal coefficients
4)载波的压缩性能与序列的平衡性密切相关。如果混沌映射生成的序列是非平衡的,会导致载波泄露,造成信息丢失和干扰。平衡性与序列长度有关,通常认为其值小于0.01即满足要求。平衡性计算公式如式(21)所示:
(21)
通过对式(15)~式(18)的分析以及结合对混沌映射的运用背景,本文序列的区间设置在[-1,1]内,所以,式(21)中X为序列中0的个数,Y为序列中1和-1的个数。序列长度值设置为[500,10 000],其他的仿真参数不变,得到平衡性结果如图7所示。
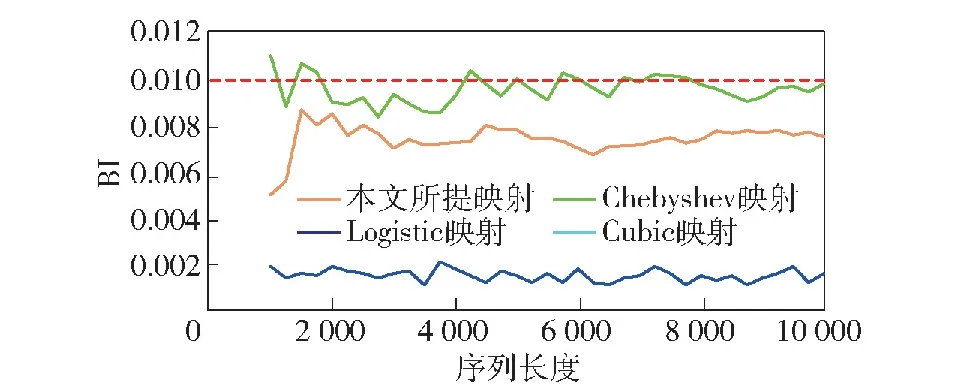
图7 不同混沌映射的平衡性对比图Fig.7 Contrast diagram of balance of different chaotic mappings
由图7可知,Cubic映射生成的序列平衡性数值随着序列长度的变化远大于临界值0.01,会导致信息泄露,信号的载波压缩性能较差。Chebyshev映射生成的序列平衡性能与本文提出的混沌映射所生成的序列相对接近,但是Chebyshev映射生成的序列在个别长度仍会出现平衡性数值超过0.01的情况。本文提出的混沌序列与Logistic混沌序列平衡性数值均小于0.01,表明二者序列的平衡性更好。
3.1.2 PRI序列性能分析
如图8(a)和图8(b)所示,通过本文提出的混沌映射对信号PRI直接进行调制时存在多值窄间隔效应,这不利于PRI值的跳变,极易导致相邻的PRI值落入相同的PRI容差范围内,所以提出了混沌映射宽间隔调制PRI的方法。仿真具体参数如下:PRI中心值为2 ms,PRI变化范围为1 000 μs,分选算法的PRI容差为200 μs,即相邻的两个信号脉冲之间的PRI至少相差100 μs,混沌序列先迭代 1 000次,从1 001次开始调制,以排除混沌系统的初值影响。为便于仿真分析,混沌序列长度设置为50。仿真结果如图9所示。
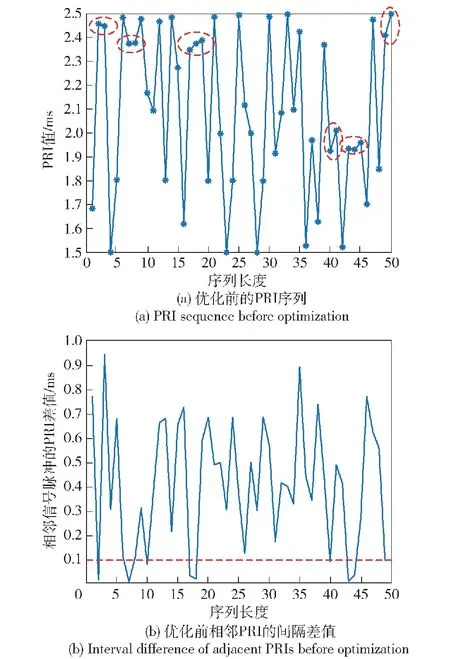
图8 优化前的PRI序列及相邻PRI的间隔变化Fig.8 PRI sequence before optimization and the interval change diagram of adjacent PRIs

图9 优化后的PRI序列及相邻PRI的间隔变化Fig.9 The optimized PRI sequence and the interval variation diagram of adjacent PRIs
由图9可知,本文所提出的方法优化了PRI序列的生成方法,消除了多值窄间隔效应,很好地满足了PRI差值间隔要求,增强了信号的抗分选性能。经过对图8和图9的仿真结果的分析,可以看到本文设计信号的灵活性。一方面,运用混沌序列对信号的PRI进行调制可以充分利用混沌系统的初值敏感性、分形系数敏感性,为信号PRI值提供了更广泛的变化范围。另一方面,对于信号PRI在不同工作条件下的设计具有更大的灵活性。PRI序列可以根据设计的信号总长度一次生成,也可以截成几段多次生成,这样得到的PRI序列同样是不同的。
3.2 信号设计原理仿真验证
信号设计原理指出当所设计的雷达信号PRI值服从长度为PRI最小间隔20倍以上的区间分布时,信号分选失效。因此,在设计信号时,PRI区间长度至少应大于20倍最小间隔。为验证信号设计原理对于设计信号的正确性和重要意义,本节进行对比仿真。仿真参数设置如下:信号共计1 000个脉冲,TOA测量误差为50 ns。信号的PRI中心值为 1 250 μs,PRI区间最小间隔为2 μs,PRI捷变的区间长度分别为最小间隔的20倍和15倍,即PRI区间为[1 230 μs,1 270 μs]和[1 235 μs,1 265 μs]。1阶直方图分析范围为0~2 500 μs,直方图统计间隔为0.5 μs。SDIF算法统计门限如式(1)所示,式中N=5000、k=0.1、a=0.8。SDIF算法分选结果如图10所示。
由图10(a)所示,当信号PRI的区间长度大于等于20倍的区间最小间隔时,区间内任意的PRI值对应的脉冲统计数量均小于SDIF的门限值,SDIF算法分选失效。同时,图10(a)亦可说明本文设计的信号在PRI抖动幅度只有20 μs,抖动量只有1.6%的小抖动幅度下仍具有抗分选能力。由图10(b)所示,当信号PRI的区间长度小于20倍的区间最小间隔时,区间内个别的信号脉冲统计数量超过门限值,能够被信号分选算法成功分选。本次仿真验证了信号设计原理的正确性,证明了设计原理为抗分选信号设计提供有力的理论支撑。
3.3 信号的抗分选性能仿真
仿真参数设置如下:信号共计1 000个脉冲,TOA测量误差为50 ns。信号的PRI中心值为2 ms,PRI变化范围为1 000 μs,1阶直方图分析范围为 0~2 500 μs,直方图统计间隔为0.5 μs。SDIF统计门限如式(1)所示,式中N=5 000、k=0.1、a=0.8。SDIF分选结果如图11所示。
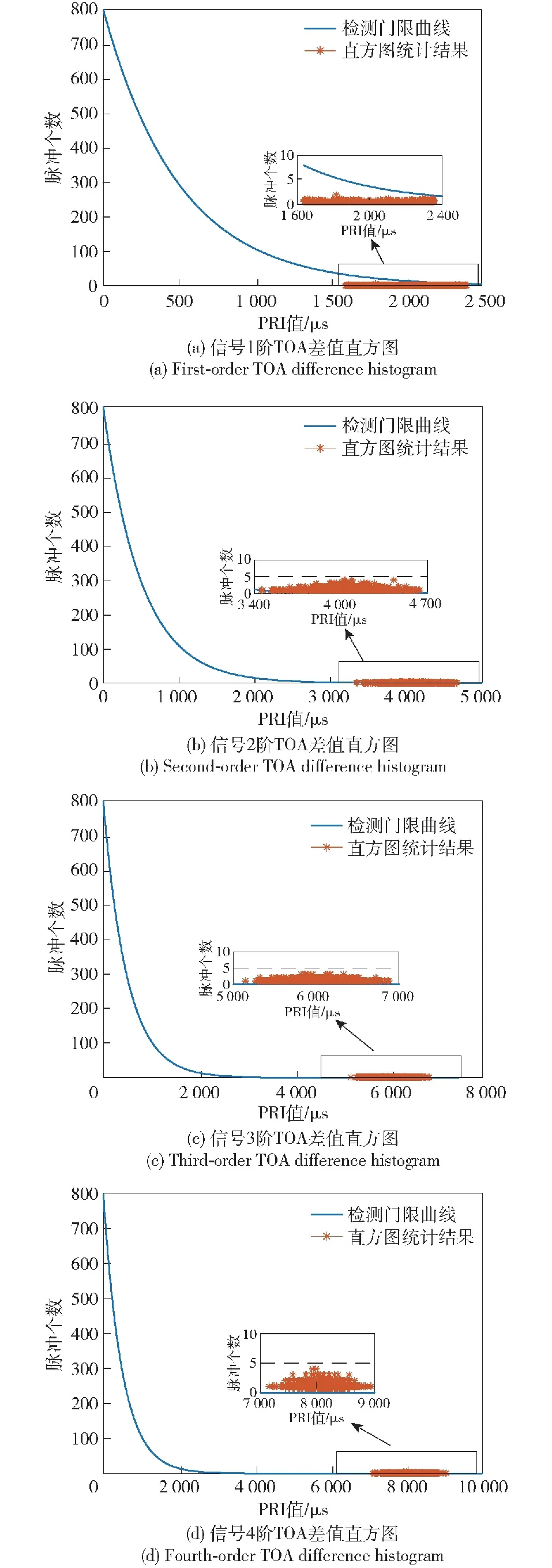
图11 1阶~4阶TOA差值直方图Fig.11 First-order to fourth-order TOA difference histograms
由图11(a)所示,在1阶SDIF直方图分选算法中根本没有超过门限的信号,所以可以实现抗分选。图11(b)~图11(d)表明,在2阶、3阶、4阶SDIF直方图分选算法中虽然有超过门限的信号脉冲,但累计数量均没有超过5个,所以信号脉冲不会进入分选流程。综合分析图11(a)~图11(d),经过本文所提出的混沌映射调制的信号可以实现抗分选的效果。
3.4 与PRI随机抖动信号抗分选对比仿真
在信号抗分选领域,PRI随机抖动信号也被认为是抗分选性能较好的信号之一[16]。本节以PRI随机抖动信号为例,与本文设计的信号就抗分选能力进行对比。抖动信号的PRI中心值为2 ms,抖动量为1 ms,即抖动信号的PRI区间为[1 500 μs,2 500 μs]。PRI随机抖动信号是PRI在[1 500 μs,2 500 μs]区间内服从随机分布。本文设计的信号是PRI在[1 500 μs,2 500 μs]区间内由混沌序列调制产生。本次待分选信号共有1 000个脉冲,仿真结果如图12所示。
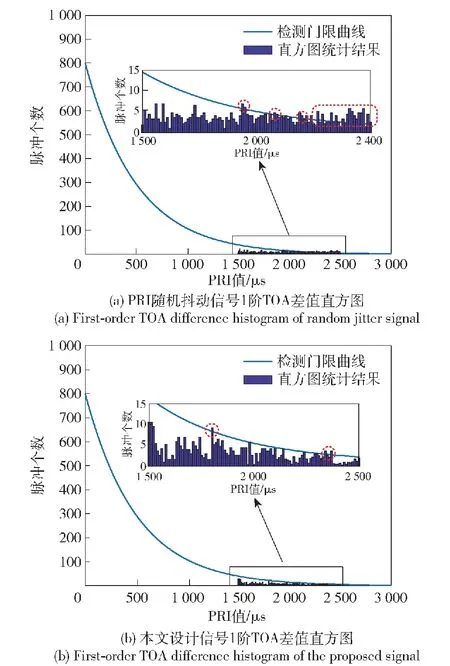
图12 抗分选性能对比仿真图Fig.12 Comparison simulation diagram of anti-sorting performance
如图12所示,图12(a)中PRI随机抖动信号直方图在红色圈所标记的地方超过分选算法的检测门限,信号极易被SDIF算法分选,图12(b)中虽然也存在信号TOA差值直方图超过分选算法门限的情形,但对比二者可以发现,在本文分析的信号设计原理指导下,由混沌序列调制的信号在直方图中仅有极少的信号直方图超过门限,而PRI随机抖动信号的直方图出现很多超过门限的情形,表明本文设计的信号在抗分选性能方面优于PRI随机抖动信号。
4 结论
为了加强雷达的射频隐身能力,本文对抗分选信号的设计原理及设计方法进行分析研究。得出以下主要结论:
1)详细研究SDIF分选算法,提出基于SDIF门限函数的抗分选信号设计原理。原理指出:当雷达信号PRI值服从长度为PRI最小间隔20倍以上的区间分布时,信号脉冲在各阶TOA差值直方图的累积量均小于分选算法门限。
2)设计了一种新型映射,该映射生成的序列在复杂性和随机性方面均显著优于经典一维混沌映射所生成的序列。
3)在抗分选信号设计原理的基础上,结合本文的混沌映射设计了一种宽间隔PRI信号。仿真结果表明,该信号具有更大的灵活性,满足了抗分选的要求,提高了信号的抗分选性能,为抗分选信号的设计提供了一种重要途径。

