多目标空地异构无人系统协同任务分配方法
范博洋,赵高鹏,薄煜明,吴祥
(南京理工大学 自动化学院,江苏 南京 210094)
0 引言
在复杂的战场环境中,功能有限的单一种类无人装备因工作方式、工作空间、载荷性能等因素限制,无法单独完成复杂多样的作战任务[1]。如旋翼无人机(UAV)具有快速灵活、视野开阔、受环境影响较小等优点,但其受限于自身载荷较小、续航时间短等不足,在大范围多目标的侦察任务中需要UAV集群的协同工作。地面无人车(UGV)具有载荷能力强、续航时间长等优点,但其受地形环境限制较大,侦察视野有限[2]。而空地异构无人系统结合空地无人平台各自优势协同作战,是适应未来战场的必然选择。因此,研究空地异构无人系统的协同任务分配具有现实意义。
无人系统协同任务分配是指考虑多目标任务和无人平台自身功能,对系统内无人装备的任务进行优化配置,使无人系统以最小代价协同完成任务[3]。无人系统的异构通常分为两类:一个是结构上的异构,主要由无人平台自身的因素造成,如运动能力、载荷能力的不同或能源动力限制等导致无人装备执行任务的空间和范围不同;另一个是功能上的异构,主要由无人平台搭载的有效载荷造成,如传感器种类或武器性能不同等因素导致无人装备所能执行任务的种类不同[4-7]。由于无人系统协同任务分配可以视为多旅行商问题,本质上是NP-hard问题[8],具有多种异构性质的因素会导致约束数量的增加,从而导致求解任务分配的计算量显著增加,特别是对于大规模问题。
目前,对两种不同类型的异构无人系统任务分配问题均有大量的研究。对于结构上的异构系统,Murray等[9]研究了异构机器人投递系统的任务分配,地面车辆和UAV分别从仓库出发向多个目标点投送物资后返回,由UAV发挥速度优势,地面车辆来弥补UAV航程和载荷能力的不足。Ha等[10]研究了地面车辆搭载UAV进行物资投递的任务分配,对于符合UAV航程约束的目标点,由地面车辆在相邻的目标点释放并回收UAV来完成投递任务,发挥UAV的速度优势,但该方法并不涉及同时使用多无人机(UAVs)的分配以及UAV降落点的选择。Bae等[6-7]研究了由行动速度不同的一组机器人组成的异构系统,对机器人从不同仓库出发向多个目标执行投递任务后再返回的任务分配问题提出了一种启发式的优化算法。Chen等[11]研究了异构UAVs对区域的协同覆盖,由于UAV的速度和传感器性能的差别导致了可覆盖区域大小不同,对不同覆盖区域的分配问题提出了一种基于整数线性规划的方法。Chen等[12]同样研究了异构UAVs对区域的协同覆盖,提出用密度聚类的方法为UAV的覆盖区域进行划分。Banfi等[13]研究了一种UGVs-UAVs任务分配框架,设计一个图神经网络估计UGVs-UAVs的分组和完成任务的代价,并使用混合整数线性规划对估计结果进行实际任务分配用以训练网络。对于功能上的异构系统,Arbanas等[14]研究了一种由UGV搭载一架UAV的异构无人系统,UGV具有收放UAV的能力,UAV从空中引导UGV进行避障。Shima等[15]和Edison等[16]研究了UAVs对多个地面目标协同执行受时序优先级约束的确认、攻击和毁伤评估3种任务的任务分配,考虑了时间、资源、可飞路径等多项约束。Feo-Flushing等[17]研究了将任务拆分为多个不同类型的子任务,分配给功能不同的多个机器人来执行,分别提出启发式和精确的算法来解决任务分配问题。Zhao等[18]研究了一种异构UAVs系统,不同类型的UAV具有执行不同任务的能力,对应多个目标需要执行多种任务,因此提出一种基于强化学习的方法解决了任务分配的问题。Chen等[19]提出一种多目标蚁群优化算法解决异构UAVs系统的任务分配问题。
现有的异构无人系统任务分配研究主要聚焦对无人平台各自合理分配,将无人系统任务分配看作多个无人平台的分工,彼此之间少有协作,尤其忽略了无人平台彼此之间的关联对任务分配结果的影响。例如关于UGV回收UAV集群位置的自主选择,这将使UGV与UAV的任务分配具有耦合因素,更能体现异构无人系统的协同与合作。
针对以上问题,本文研究UGV与多架旋翼UAV组成空地异构无人系统对作战区域内的多个目标进行协同侦察与打击的任务分配问题。该空地异构无人系统既包含结构上的异构,又包含功能上的异构。由UAV执行侦察任务,UGV在执行打击任务的同时需要在合适的地点释放、回收UAV,使得整个系统在最短的时间有效完成任务。在目标数量较多的环境下,本文先将作战区域内目标点聚类划分为若干子任务区域,并对子区域间进行任务分配。再在子区域内将UAV的任务分配模型与UGV的任务分配模型相结合,考虑二者之间的耦合,在给出任务分配的同时,还确定了UGV收放UAV的位置,使得空地异构无人系统的任务分配结果符合约束条件。本文的研究思路如图1所示,贡献主要包括两个方面:1) 建立了空地异构无人系统协同任务分配模型;2)提出一种结合聚类算法和启发式算法的多目标空地异构无人系统协同任务分配方法,求解对大范围、多目标、可回收的空地异构无人系统任务分配。
1 协同任务分配问题模型
1.1 问题描述
假设空地异构无人系统的作战场景为较大范围内具有数量较多的待侦察和待打击目标。UGV续航能力强并可以携带攻击武器,其在执行任务的过程中能量不会耗尽,而UAV的续航能力有限,只具有侦察载荷。本文假设无人系统拥有战前情报支援,可以获得战场卫星地图以及可靠的目标位置。UGVG={g}与UAVsU={u1,u2,…}对作战区域内多目标点T={t1,t2,…}进行协同侦察与打击,作战区域内目标点的位置、数量以及待执行任务类型等信息都是已知的,其中全部目标点均为待侦察目标Ts⊆T,部分特定的目标点为待打击目标Ta⊆T。
考虑空地异构无人系统的特点,作战过程如图2所示,各UAV的飞行路径由不同颜色区分。UGV搭载UAV进入作战区域,并自主决定释放点tre释放多架UAV,由UAV对分配的目标点依次进行侦察,同时UGV向已被侦察的待打击目标点依次运动并进行火力打击,UAV执行完作战区域内的侦察任务后前往降落点tl降落回UGV。在整个作战过程中,UGV以速度vg在地面行驶,UAV以速度vu匀速飞行,飞行高度为hu。无人系统在作战区域内的候选降落点Tland=(Ta∪tre)中自主选择UAV的降落点tl∈Tland。
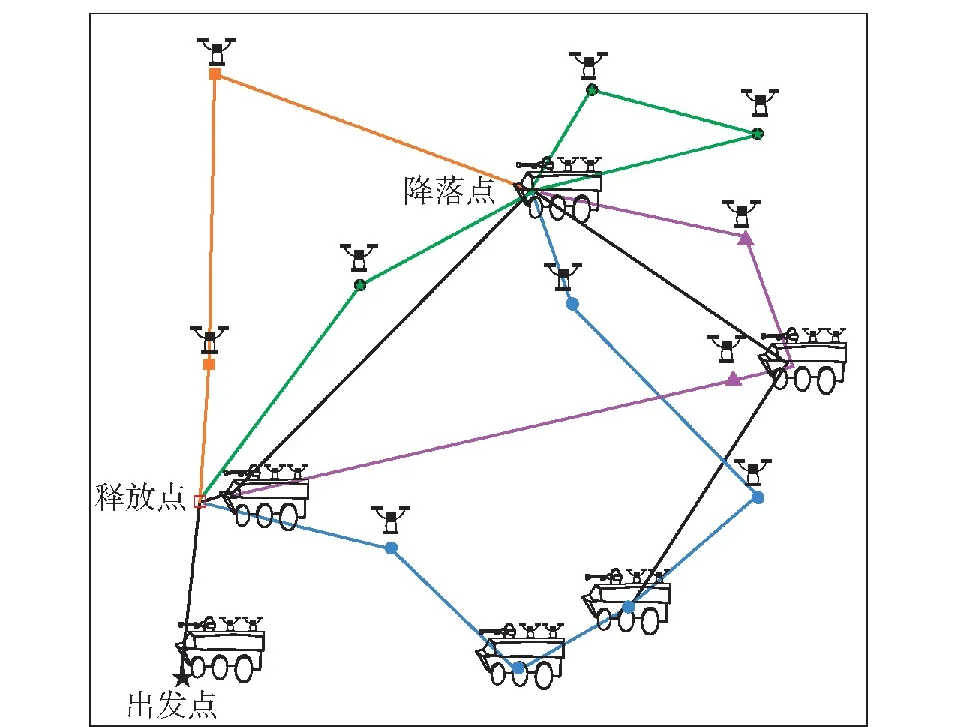
图2 多目标空地异构无人系统协同作战过程示意图Fig.2 Schematic diagram of collaborative operation process of multi-target air-ground heterogeneousunmanned system
多目标空地异构无人系统协同任务分配问题可以描述成多旅行商问题的形式,每一个任务分配方案即是该多旅行商问题的一个解,表示为指派空地异构无人系统中的各个无人装备对不同数量的目标点执行不同类型任务的时序序列。本文将空地异构无人系统的协同任务分配模型拆分为UAVs任务分配模型和UGV任务分配模型,对其分别求解,并同时考虑二者间的耦合成分,即UGV收放UAV的位置和时间。本文将无人装备在目标点间的运动估计简化为无障碍的直线运动。
1.2 问题建模
1.2.1 UAVs任务分配模型
为最小化各UAV协同执行任务及返回降落点所使用的总时间,UAVs任务分配模型的目标函数如 式(1)所示:
(1)
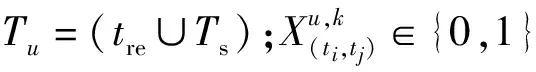
UAV的航程约束如式(2)所示,UAV从起飞执行任务到安全降落所使用时间不能超过其最大续航时间。
(2)
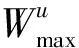
UAV的侦察任务约束条件如式(3)和式(4)所示,所有待侦察的目标都需要被侦察,且只需侦察一次。
(3)
(4)
式中:Ns为待侦察的目标数量。
UAV的降落约束如式(5)~式(7)所示,所有出动的UAV都要安全降落,且UGV到达降落点时间不能晚于UAV。
(5)
(6)
(7)
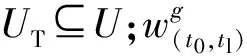
1.2.2 UGV任务分配模型
为最小化UGV执行任务所使用的总时间,UGV任务分配模型的目标函数如式(8):
(8)
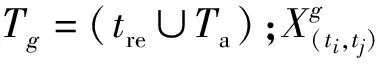
UGV的回收约束如式(9)所示,UGV要先于UAV到达降落点。
∀u∈UT,Jwait≥0
(9)
UGV的打击任务约束如式(10)和式(11)所示,所有待攻击的目标都需要被攻击,且只需攻击一次。
(10)
(11)
式中:Nd为待攻击的目标数量。
目标点的任务时序约束如式(12)所示,对任意待攻击的目标,都须先由UAV进行侦察后,UGV再执行攻击任务。
(12)
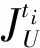
2 多目标空地异构无人系统协同任务分配方法
采用两步法对多目标空地异构无人系统协同任务分配问题进行求解:
1)使用密度最大值聚类方法[20]将作战区域按目标密度进行划分,得到n个子任务区域{C1,C2,…,Cn}。再将子任务区域的任务分配问题近似为UGV遍历各区域的排序,其优化目标为最小化UGV遍历各区域所使用的时间。使用子区域内密度值最大点来代表区域位置,可以利用UGV任务分配模型,使用混合粒子群算法对UGV在子任务区域间转移的任务分配问题进行求解,得到最优解PC={1,2,…,n}为UGV在子任务区域间执行任务的次序。
多目标空地异构无人系统协同任务分配的流程图如图3所示,图中itCC、itCM分别是子区域间任务分配的当前迭代次数和最大迭代次数,itUC、itUM是UAV任务分配的当前迭代次数和最大迭代次数,itGC、itGM是UGV任务分配的当前迭代次数和最大迭代次数。
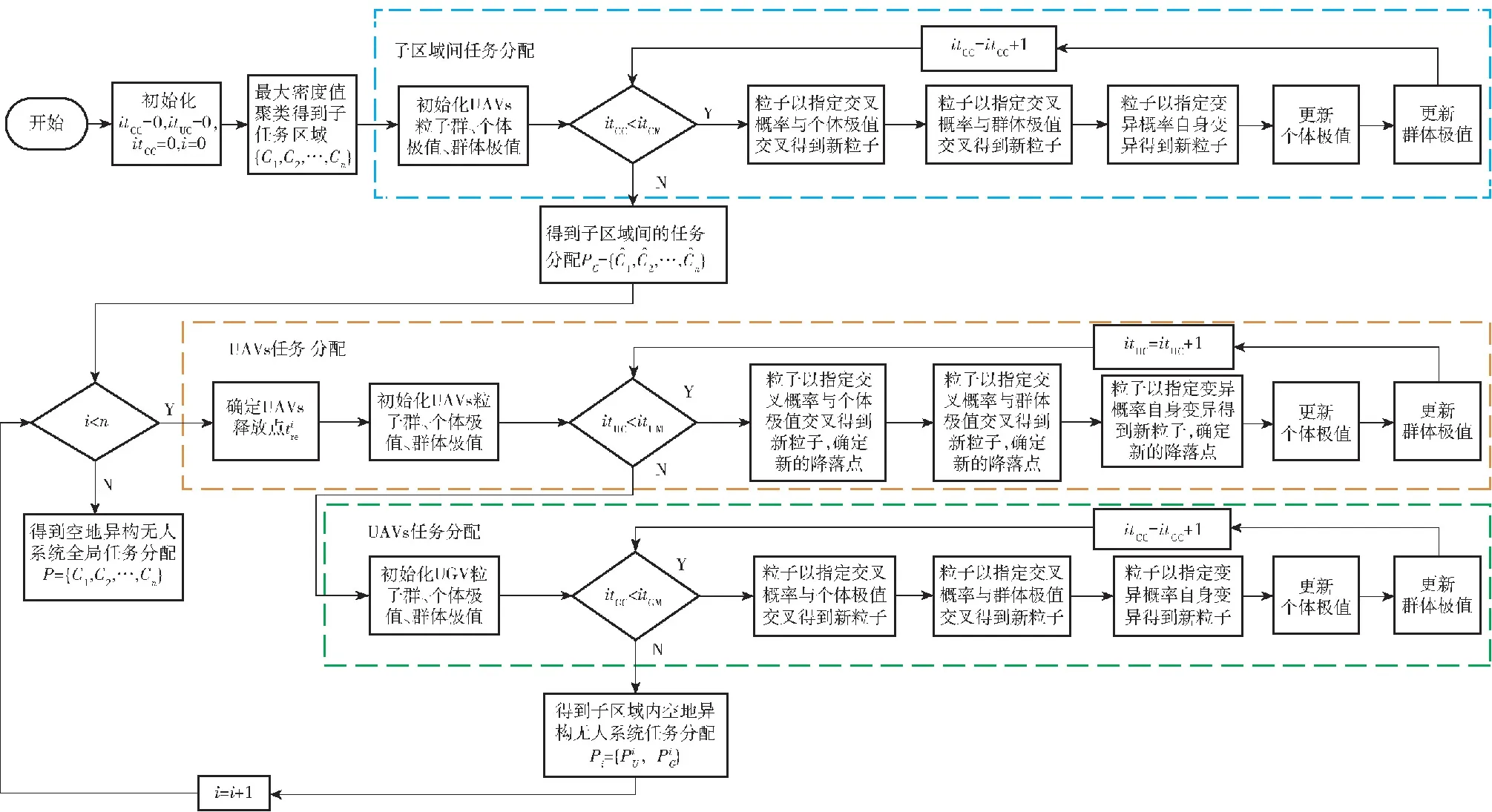
图3 多目标空地异构无人系统协同任务分配方法流程图Fig.3 Process of the task allocation method for multi-target air-ground heterogeneous unmanned system
2.1 子任务区域划分
在面向大范围多目标的复杂战场环境中,UAV有限的航程是限制空地异构无人系统完成任务能力的重要约束。在目标分布不均衡、存在多个密集目标群和稀疏目标点的作战场景下,划分子任务区域,将密集目标群和稀疏目标点区分开来,使用UGV携带UAV在区域间机动转移,减少UAV在稀疏目标点间的往返,有效的提高空地异构无人系统在航程约束下进行任务分配的能力。密度值最大聚类以空间区域的目标稠密程度作为发现簇的依据,能够有效的发现任意形状的簇,对于稀疏目标点可以单独划分,符合本文分离密集目标群和稀疏目标点的需要。该方法可以自动发现簇的数量,无需人工确定,其参数选择取决于密度阈值的设定,与目标点的实际分布无关。
2.1.1 密度最大值聚类
定义目标点tp与tq间的距离dist(tp,tq)为欧式距离,tp,tq∈T。目标点tp的邻域N(tp,ε)为以tp为核心、半径ε区域内所包含的目标点,即
N(tp,ε)={tq|dist(tp,tq)≤ε}
(13)
目标点tp的密度ρp定义为tp的邻域N(tp,ε)内包含所有目标的数量,即
ρ(tp)=|N(tp,ε)|
(14)
定义最大密度值点为
tmax={tp|tp∈T;∀tq∈T,ρ(tp)≥ρ(tq)}
(15)
定义按与最大密度值点距离排列的目标点序列为
Smax={tp,tq,…,tn|dist(tmax,tp)≤
dist(tmax,tq)≤…≤dist(tmax,tn)}
(16)
定义簇Ch与Cm间距离为两个簇中最近两个目标点之间的距离,即
dist(Ch,Cm)=min(dist(tp,tk))
(17)
式中:tp∈Ch;tk∈Cm。
密度最大值聚类分为两步:

ρ(tp)≥minDens,tp∈Smax
(18)
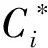
2) 合并基本簇。对第1步得到的基本簇集C*,将簇间距离小于簇距离阈值minDist的簇合并为一个簇,即
(19)
最终得到簇集C={C1,C2,…}。
2.1.2 参数选择
密度值最大聚类的参数包括:邻域半径ε、密度阈值minDens和簇距离阈值minDist。其中邻域半径和密度阈值决定基本簇的产生,在本文假设的作战场景下,一定范围内目标数量超过一个阈值则可以视为一个重要阵地,应当被划分为同一个任务区域。簇距离阈值决定如何合并基本簇,同时也决定如何划分稀疏目标点,该参数的选取与UAV的性能相关联,本文中验证实验的参数由多次实验调整取得。
2.2 混合粒子群优化算法
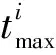
2.2.1 适应度值设计
2.2.1.1 对子任务区域的任务分配
粒子适应度值表示为UGV完成在各子区域间转移所用时间之和,各子区域的位置由区域内密度值最大的任务点代表:
(20)
式中:Tmax⊆T为各子任务区域内密度值最大的任务点的集合;pathG(ti,tj)为UGV从目标ti到目标tj所需时间。
2.2.1.2 对UAV的任务分配
粒子适应度值表示为各UAV完成被分配的任务所用时间与到达降落点所用时间之和。

(21)
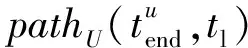
2.2.1.3 对UGV的任务分配
粒子适应度值表示为UGV完成被分配的任务所用时间与等待全部UAV降落完成所用时间之和:
(22)
式中:costwait为UGV等待全部UAV降落的时间。
2.2.2 粒子表示
粒子表示采用整数编码的形式,每一个粒子代表多目标空地异构无人系统协同任务分配的一种方案,包括系统中全部UGV和UAV的任务时序序列,该粒子须满足任务约束条件式(3)、式(4)、式(10)和式(11)。例如,一个包含一辆UGV和4架UAV的空地异构无人系统,待分配的侦察目标为16个,序号为1~16,其中目标[4,7,10,13]同时为待打击的目标,则表示一种任务分配方案的粒子如图4 所示。

图4 粒子表示方法Fig.4 A sample of the particle code
2.2.3 交叉操作
粒子通过与极值交叉得到新的粒子,交叉方法采用整数交叉法。首先选择交叉位置和交叉片段大小,然后将粒子与极值的交叉位置上的值进行交换。产生的新粒子可能会出现目标重复分配及目标缺失,因此还需对新粒子进行调整。在新粒子中保留由交叉位置得到的新分配目标点,对在非交叉位置上存在的与新分配目标点重复的目标点,用缺失的目标点进行替换。当存在多个重复目标点时,被替换位置与替换目标点使用随机匹配,使得新粒子满足任务约束条件式(3)、式(4)、式(10)和式(11)。假定随机选取交叉位置为第4个UAV的第2个目标,交叉片段大小为2,操作方法如图5所示。
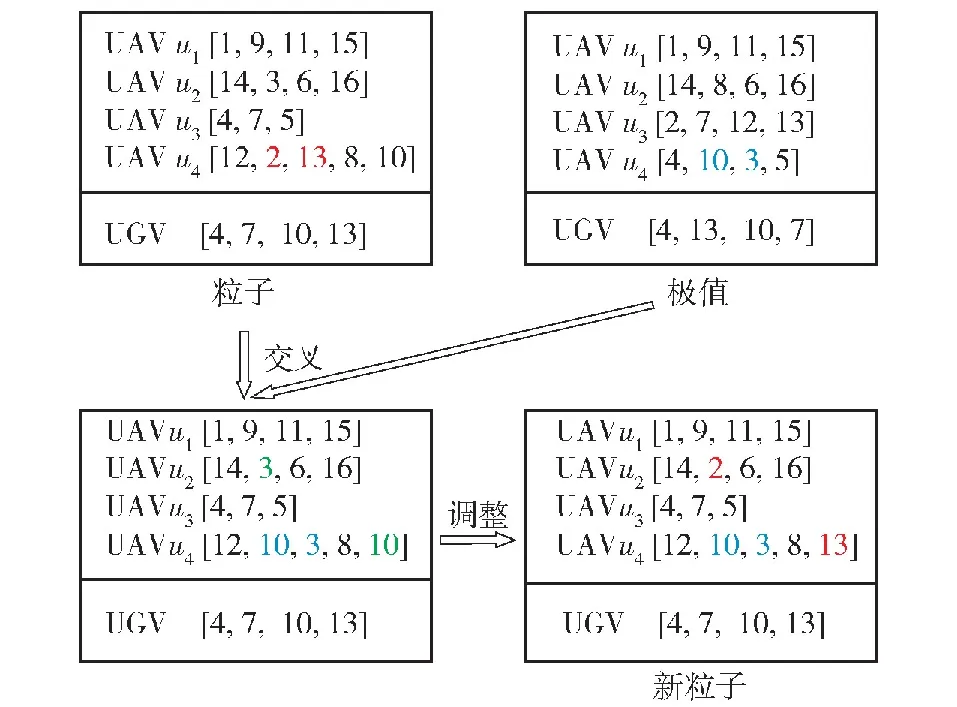
图5 交叉操作方法Fig.5 A sample of the crossover operation
2.2.4 变异操作
粒子通过自身变异得到新的粒子,变异方法采用粒子某个任务序列中的两目标次序互换。首先选择变异位置,然后把两个变异位置互换,显然新粒子满足任务约束条件式(3)、式(4)、式(10)和式(11)。假定选择的变异位置为第2个UAV的第2位和第4位,操作方法如图6所示。
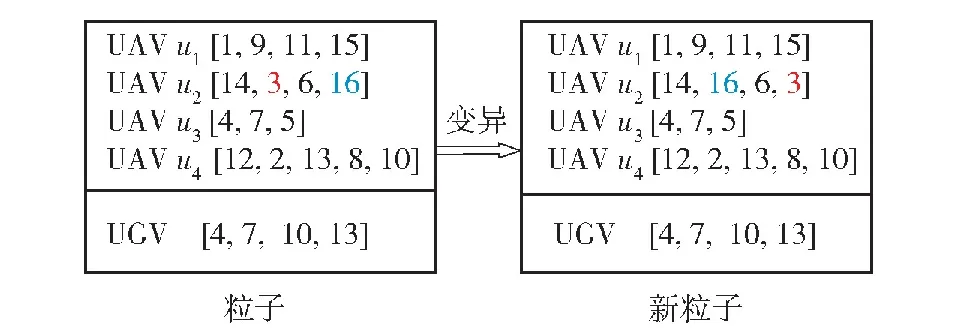
图6 变异操作方法Fig.6 A sample of the mutation operation
2.2.5 粒子更新策略
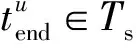

对UGV任务分配时,只有当新粒子的适应度值小于旧粒子且新粒子满足回收约束条件式(9)和任务时序约束条件式(12)时才更新粒子。
对子任务区域任务分配时,只有当新粒子的适应度值小于旧粒子才更新粒子。
2.2.6 极值更新策略
极值更新分为个体极值更新和群体极值更新:
1) 个体极值更新:当新粒子的适应度值小于旧粒子极值的适应度时,更新新粒子为个体极值。
2) 群体极值更新:在不同阶段的任务分配中使用混合粒子群算法,群体极值更新策略不同:
① UAV任务分配:在个体极值中符合UAV的航程约束条件式(2)的解未搜索到,且所有个体极值中最小适应度值小于群体极值的适应度值时,更新该个体极值为群体极值;在个体极值中搜索到符合UAV的航程约束条件式(2)的解,但群体极值不符合航程约束时,更新符合航程约束条件式(2)的所有个体极值中适应度值最小的个体极值为群体极值;当群体极值符合航程约束条件式(2),且所有符合航程约束条件式(2)的个体极值中最小适应度值小于旧群体极值的适应度值时,更新该个体极值为群体极值。
② UGV任务分配和子任务区域任务分配:只有当所有个体极值中最小适应度值小于群体极值的适应度值时,才更新该个体极值为群体极值。
3 仿真实验
为验证本文所述方法,在12 000 m×12 000 m场景下验证聚类划分子任务区域的效果,在6 000 m×6 000 m和12 000 m×12 000m两种不同的场景中对由一辆UGV搭载4架UAV组成的空地异构无人系统进行多目标协同任务分配,并分析结果。其中6 000 m×6 000 m场景主要验证在较小范围内多目标空地异构无人系统协同任务分配的能力;12 000 m×12 000 m场景验证在较大范围内存在偏离密集目标区域的稀疏目标点的情况下,结合子任务区域划分的多目标空地异构无人系统协同任务分配方法的能力。目标点坐标使用均匀分布随机生成,得到的目标区域既有多个密集的目标群,也有稀疏的目标点,能够近似模拟真实场景中重要区域部署兵力较多、非重要区域部署兵力较少的兵力部署的特点。假设半径1 000 m范围内有5个目标点的区域为一个重要阵地。UGV的速度为20 km/h,UAV的速度为30 km/h,最大飞行时间为30 min。计算机配置为AMD RyzenTM7 PRO 4750G@3.6 GHz,32 GB内存,采用Ubuntu 20.04操作系统。
3.1 聚类效果评估
在12 000 m×12 000 m作战场景下使用均匀分布随机生成50个目标点,图7给出了使用密度值最大聚类进行子任务区域划分的效果。
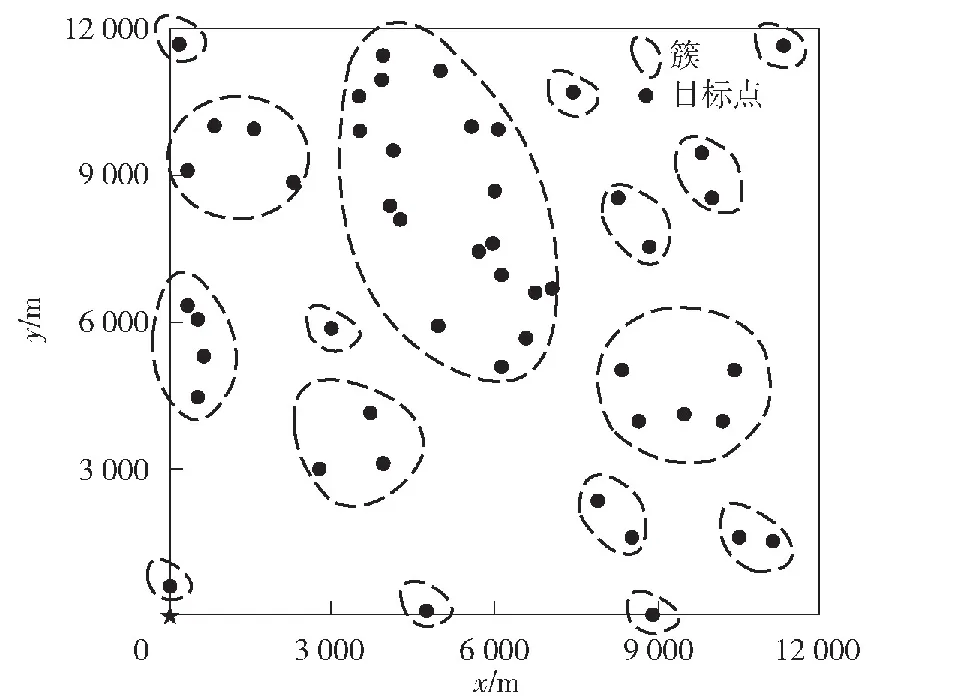
图7 密度值最大聚类效果图Fig.7 Result of density peak clustering
本文使用Davies-Bouldin指数(DBI)为评价标准:
(23)
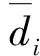
DBI值越小,簇内的目标点分布越紧密,簇间的最小距离越大,这符合本文对子区域划分的要求。
表1给出了在12 000 m×12 000 m作战场景下使用密度值最大聚类、DBSCAN和k-means算法进行聚类的效果评估。其中密度值最大聚类的邻域半径、密度阈值由重要阵地的假设得到,簇距离阈值由多次实验获得;DBSCAN算法采用保留噪声点的方式,其密度阈值由多次实验获得;k-means算法随机选择初始中心点。可以看出,密度值最大聚类可以得到子区域内目标点分布更紧密、子区域间距离更大的任务区域划分。

表1 12 000 m×12 000 m范围聚类划分结果对比Table 1 Comparison of clustering results in the range of 12 000 m×12 000 m
3.2 较小范围内的任务分配仿真
6 000 m×6 000 m范围内的目标分布如图8所示,随机分布50个目标点个目标点由蓝色点标出,其中有17个随机点为待打击目标,由黑色方框标记。黑色点为UGV的出发点。
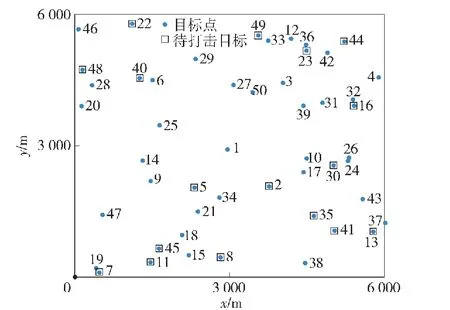
图8 6 000 m×6 000 m范围内目标分布图Fig.8 Target distribution map in the range of 6 000 m×6 000 m
多目标空地异构无人系统协同任务分配方法的参数如表2所示。多目标空地异构无人系统协同任务分配结果如表3和图9所示。

表2 6 000 m×6 000 m范围协同任务分配方法参数Table 2 Parameters of thecollaborative task allocation method in the range of 6 000 m×6 000 m

表3 6 000 m×6 000 m范围协同任务分配结果Table 3 Collaborative task allocation in the range of 6 000 m×6 000 m
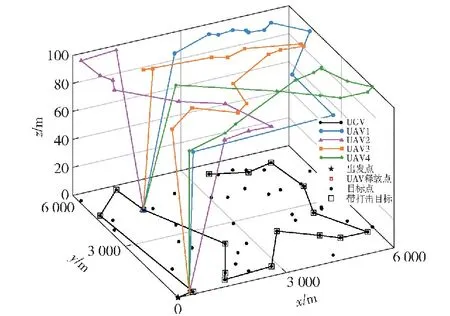
图9 6 000 m×6 000 m范围内协同任务分配示意图Fig.9 Schematic diagram of the collaborative taskallocation in the range of 6 000 m×6 000 m
由于区域内目标点的分布较为密集,密度值最大聚类算法将整个任务区域划分为一个子区域。规划的UAVs释放点在距离目标点[19]的50 m处,坐标为(365 m,106 m),降落点为目标点40的位置,UGV等待UAVs降落时间Jwait=5.36 s,各UAV的飞行时间为[1 718.11 s,1 340.85 s,1 562.53 s,1 643.87 s],各子区域内的任务分配结果满足UAVs的航程约束式(2)、侦察任务约束式(3)和式(4)、降落约束式(5)~式(7)、UGV的回收约束式(9)、打击任务约束式(10)和式(11)以及目标点的任务时序约束式(12)。
图9为协同任务分配结果的示意图。各UAV飞行时间的收敛曲线如图10所示,从图中可以看出混合粒子群优化算法在第555次迭代中得到满足航程约束式(2)的解,在1 800次迭代后基本收敛到稳定值。整个多目标空地异构无人系统协同任务分配计算用时859.9 s。

图10 各UAV飞行时间曲线Fig.10 Flight time curves of UAVs
3.3 较大范围内的任务分配仿真
12 000 m×12 000 m范围内的目标分布如图11所示,随机分布50个目标点由蓝色点标出,其中有17个随机点为待打击目标,由黑色方框标记。黑色点为UGV的出发点。
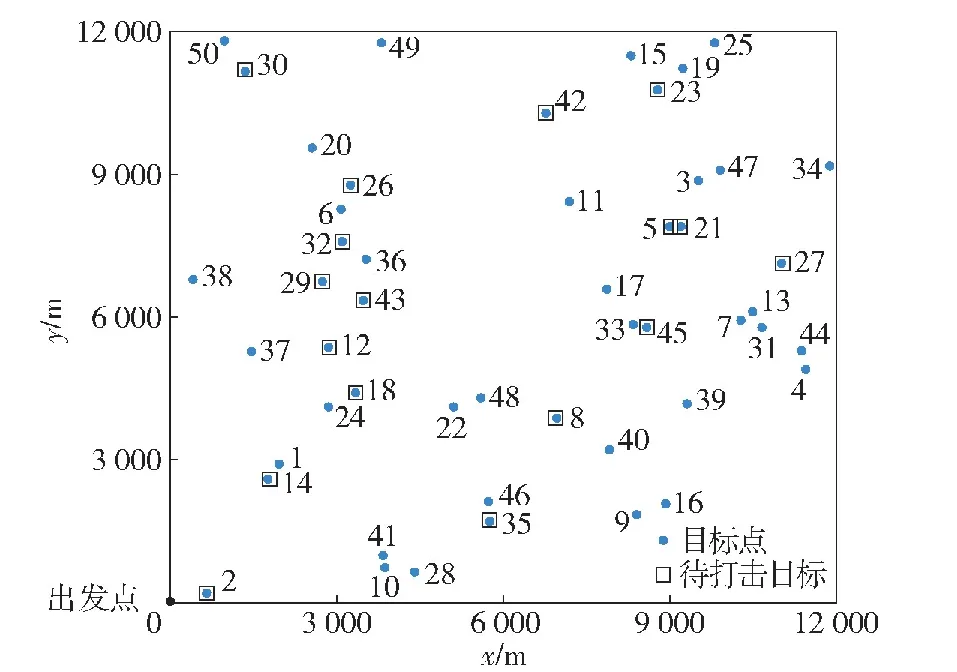
图11 12 000 m×12 000 m范围内目标分布图Fig.11 Target distribution map in the range of 12 000 m×12 000 m
若不对作战区域进行划分,混合粒子群优化算法的参数如表4所示。任务分配结果如表5所示,各UAV的飞行时间为[3 401.53 s,2 884.75 s,2 491.79 s,2 704.78 s],超过其最大续航时间,违反了UAVs的航程约束条件式(2),任务分配失败。
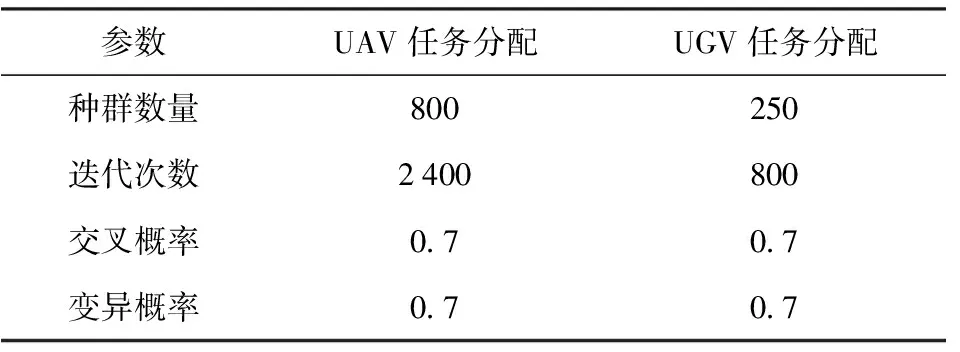
表4 12 000 m×12 000 m范围不划分子任务区域的协同任务分配方法参数Table 4 Parameters of the task allocation method without clustering in the range of 12 000 m×12 000 m
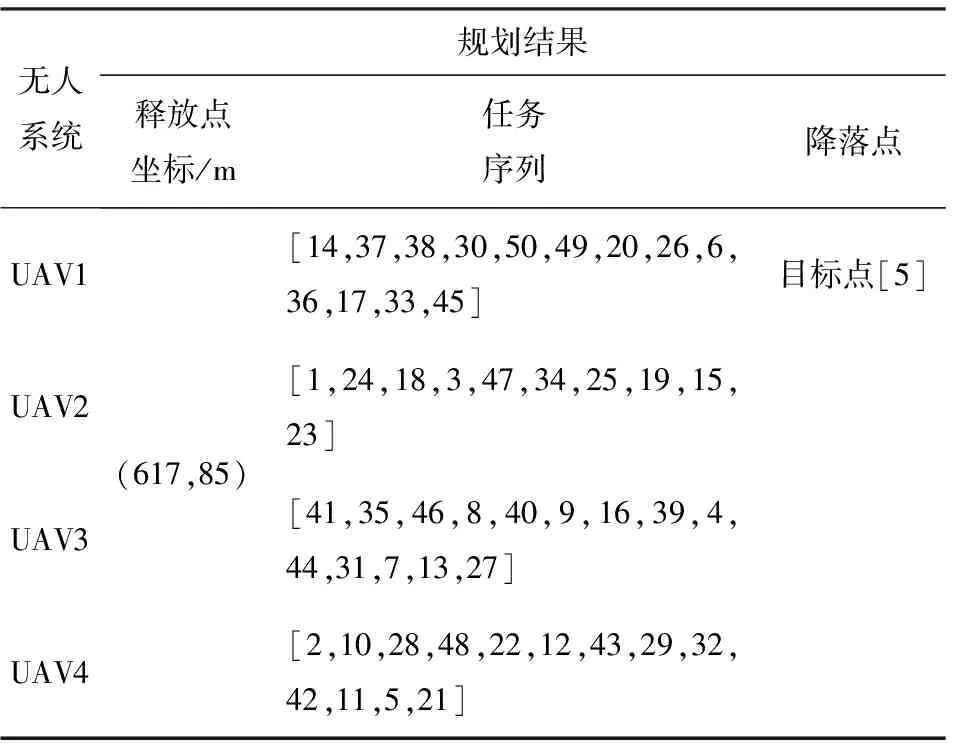
表5 12 000 m×12 000 m范围不聚类划分子任务区域的协同任务分配结果Table 5 Task allocation result without clustering in the range of 12 000 m×12 000 m
结合密度值最大聚类算法对作战区域进行划分,空地异构无人系统协同任务分配方法的参数如表6所示。密度值最大聚类将作战区域划分为 16个子任务区域,子任务区域的划分和任务分配结果如图12所示。

表6 12 000 m×12 000 m范围协同任务分配方法参数Table 6 Parameters of the collaborative task allocation method in the range of 12 000 m×12 000 m
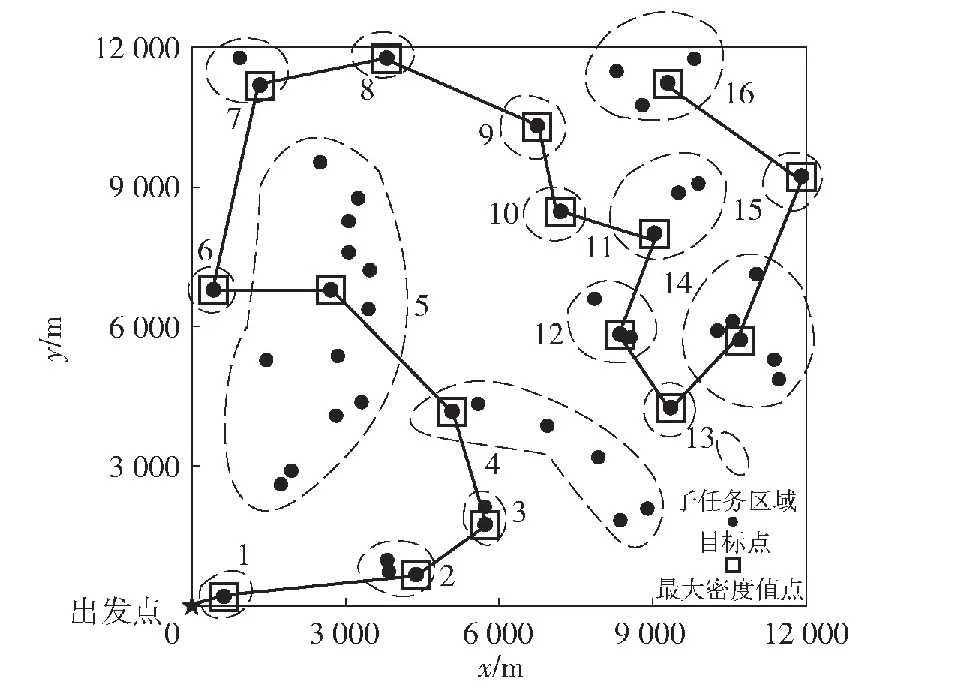
图12 子任务区域的划分和任务分配Fig.12 Clustering and task allocation

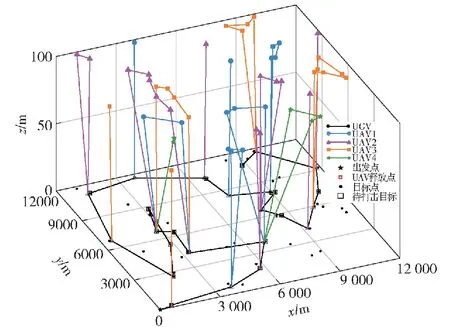
图13 12 000 m×12 000 m范围内多目标空地异构无人系统协同任务分配示意图Fig.13 Schematic diagram of the collaborative task allocation for multi-target air-ground heterogeneous unmanned system in the range of 12 000 m×12 000 m
图13为多目标空地异构无人系统协同任务分配结果的示意图。整个协同任务分配计算用时277.93 s。
4 结论
本文首先基于多目标、大面积的战场环境假设,构建空地异构无人系统协同任务分配模型,提出一种多目标空地异构无人系统协同任务分配方法,最后通过两种不同的环境中的仿真实验,证明了本文方法的有效性。得出以下主要结论:
1) 在较小作战环境内,本文方法能够满足约束条件,有效地为空地异构无人系统进行协同任务分配。
2) 在较大作战环境内,由于约束条件限制,UAVs无法在一次出动中完成设定任务,本文方法通过结合密度值最大聚类、混合粒子群优化算法,将整个战场划分为多个子任务区域,并为空地异构无人系统在区域间转移和区域内作战进行协同任务分配,使其满足约束条件。

