电磁能与炸药联合加载药型罩基础理论
豆剑豪,贾鑫,梁争峰,黄正祥,薛标
(1.西安近代化学研究所,陕西 西安 710000;2.南京理工大学 机械工程学院,江苏 南京 210094)
0 引言
破甲弹通过聚能装药爆炸后压垮药型罩形成的金属聚能射流来对装甲目标进行毁伤[1]。为了提升聚能装药的威力,国内外学者进行了大量研究,徐文龙等[2]提出一种超聚能结构,并通过数值模拟和试验进行了验证,超聚能结构下射流的有效质量及侵彻能力远大于传统聚能射流。张昊等[3]和苏成海等[4]对活性材料射流侵彻混凝土进行了研究,以提高射流侵彻开孔和后效效应。Kemmoukhe等[5-6]对改变药型罩结构来提高聚能装药威力进行了研究。郑宇等[7]对双层药型罩的射流形成进行了研究分析。杨丽等[8]对带隔板装药的杆式射流成型及侵彻特性进行研究,以提高射流威力。但根据聚能装药的作用原理,如图1所示(β为压垮角),聚能装药在爆轰过程中爆轰产物向四周飞散,非毁伤元驱动方向的装药几乎没有利用,很难将较多的爆轰能量集中于某一特定方向,同时圆柱部分装药主要用于传递爆轰和调整波形,炸药能量没有加载至药型罩上,因此现阶段传统聚能装药形成的射流对炸药能量利用率较低。现有国内外公开资料表明,聚能装药对钢靶的最大侵彻威力为 10倍装药直径[9],很难再通过提高炸药爆速、爆压或改变药型罩结构及材料的手段来进一步提升聚能装药的侵彻威力。
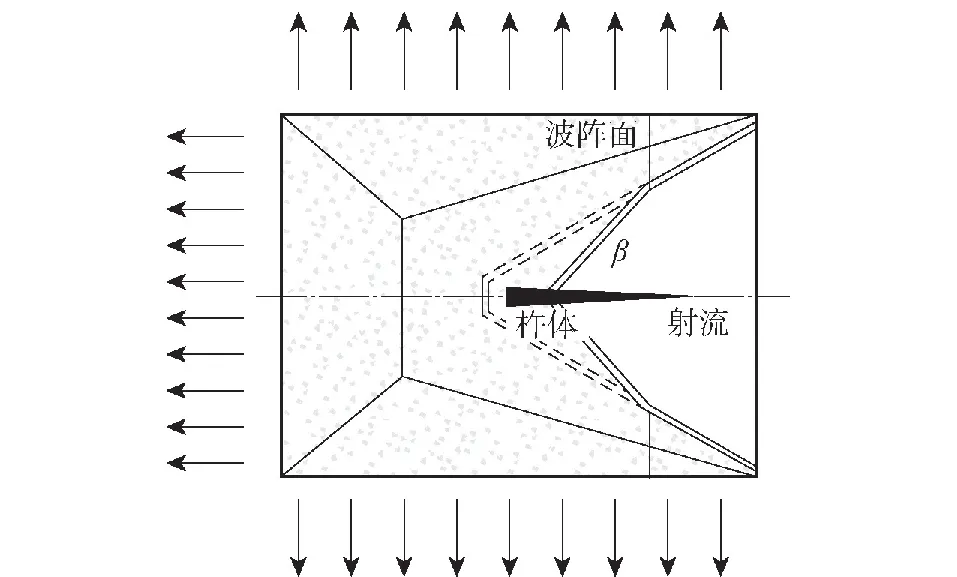
图1 传统聚能装药原理Fig.1 Schematic diagram of traditional shaped charge
爆磁压缩发生器(FCG)是一种能够把炸药化学能转化成电磁能的脉冲能源装置[10-11],其基本概念是通过炸药爆轰驱动电枢压缩定子产生磁场,将化学能转化为电磁能,从而在负载中实现脉冲电流和电磁能量的放大。自前苏联的A.D.Caxapov和美国的J.L.Folwer提出FCG以来[12],至今被国内外大量研究。国内中国流体物理研究所和国防科技大学自上世纪60年代开始研究[11],已于2000年研制的8-6型FCG可在5.2 μH电感性负载上产生 100 kA 的脉冲电流,储能达25 kJ,脉宽17 μs。孙奇志等[13]于2009年设计的EMG-125型螺线型发生器可以在25 nH的负载上输出大于3 MA的电流,电磁能量放大50倍。夏明等[14]利用FCG作为初始能源,成功加载薄壁金属管变形。可见FCG技术相对成熟,能够实现对炸药能量的转化。
本文基于Dou等[15-17]以及Grace等[18]对电磁加载药型罩的研究以及FCG原理,提出一种电磁与炸药联合加载药型罩的原理结构,如图2所示。图2中,S1、S2为闭合开关,R1、L1分别为传输线路的电阻和电感,C为电容器,I为传输线路电流。该结构将原聚能装药的圆柱部分炸药设计为FCG结构,该部分炸药一方面用于压缩磁场放大电流,实现炸药能向电磁能的转化,另一方面传递爆轰波,引爆炸药2,爆轰加载药型罩。通过上述方法,将炸药1的部分能量也用于加载药型罩,提高成型射流的速度和威力以及对炸药能量的利用率。本文建立了炸药与电磁共同加载药型罩的简单理论模型,并对φ56 mm装药结构进行联合加载设计,计算了炸药和电磁共同加载下的射流成型,并通过理论分析了联合加载时序对射流成型的影响。

图2 炸药与电磁联合加载原理示意图Fig.2 Schematic diagram of the combined loading principle of explosives and electromagnetic force
1 联合加载下射流成型理论模型
1.1 加载原理及基本假设
炸药与电磁联合加载的电路与原理示意图如图2所示,炸药1为原聚能装药的圆柱部分装药。电磁的初始能源由电容器C提供,左端虚线框内为FCG结构。加载共分为两个阶段:
1)第1阶段为初始磁通形成阶段,闭合放电开关S1,电容器对整个回路放电,电路包括传输线路电阻R1和电感L1,FCG的等效电阻R2和电感L2,药型罩装置(负载)的电阻R3和电感L3。此时电流较小,电磁力无法压垮药型罩。当电流到达电流峰值后,闭合开关S2,进入第2阶段。
2)第2阶段为磁通压缩阶段,药型罩在电磁力及炸药的加载下压垮成型。此时电容器被短路,由FCG向负载供能,在闭合开关S2的同时控制炸药起爆,起爆点位于圆柱部底端轴线处。炸药1爆轰后驱动电枢向外运动,根据磁场冻结效应,极短时间内定子线圈与电枢之间的磁通量几乎不变,空间被压缩导致磁感应强度增大,电流被放大,放大的电流在药型罩上产生垂直于药型罩表面指向里的电磁力。同时爆轰波在炸药1中向右传播,引爆炸药2,炸药2 爆炸后,爆轰压力作用药型罩上与电磁力共同加载药型罩向轴线压垮。当电枢完全膨胀,FCG的电感不再减小时,电流增加到最大值。存储在电感中的电磁能继续向负载放电,此时的电路为RL电路,电流不断减小,电磁力与炸药爆轰压力继续共同加载药型罩,驱动药型罩在轴线处碰撞形成射流,最后电路断开,联合加载结束。
炸药爆轰会产生破坏效应,在试验或应用中应考虑爆轰的破坏,可在电路中设置隔爆装置,降低爆轰波的在电路器件中的传播,在电路被破坏前完成加载。本文只进行初步的理论研究,因此在建立理论模型前,先做出一些基本假设:
1) 在磁爆加载过程中,电路、炸药、磁场和力场互相不影响。
2) 电路加载过程中,药型罩装置与FCG之间的磁场变化相互独立,互不影响。
3) 在电路作用过程中,除了理论模型设计的关键参数外,其余各元件为理想元件。
4) 炸药能够理想传爆及爆轰,爆轰波以平面波的方式传播。
5) 不考虑炸药爆轰对电路的破坏。
1.2 炸药爆轰压力
传统炸药加载下的药型罩压垮理论已经相对成熟,这里采用有效装药的绝热压缩方法计算炸药爆轰压力[1]。假设炸药瞬时爆轰,且稀疏波沿装药表面的内法线方向向爆炸产物内部传播,爆轰产物是以稀疏波初始交界面为刚性边界进行定向膨胀的,药型罩向轴线压垮运动时,有效装药部分向内绝热膨胀做功。有效装药可以用装药剖面图的各个角平分线来确定,如图3所示,MN平分∠PMQ,△MQN围成的区域即为该装药结构下的有效装药,故为了不减小原有装药结构下形成的射流威力,在采用图2所示结构时,炸药2的装药长度不能小于PM。
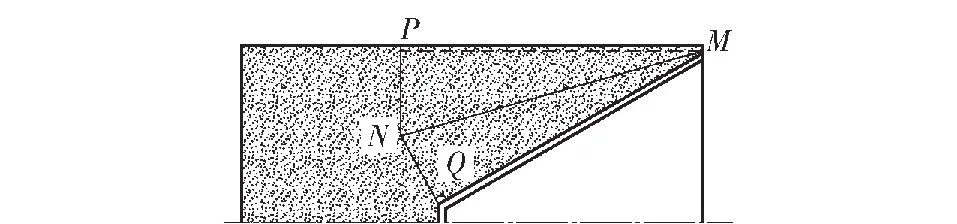
图3 有效装药示意图Fig.3 Schematic diagram of effective charge
根据有效装药绝热膨胀的假设,作用于药型罩微元表面的压力pi[1]应满足:
(1)
式中:p0i为爆轰产物的初始压力;V0i为药型罩微元对应的有效装药的初始体积;Vi为爆轰产物所占体积;γ为绝热系数,一般的猛炸药可取3。瞬时爆轰后,爆轰产物的初始压力可近似取为
(2)
式中:pCJ为炸药的CJ压力;ρe为装药密度;D为爆速。
1.3 FCG理论模型
在加载第1阶段,加载电路相当于RLC电路,电流可用式(3)[15]表达:
(3)

ψ=I0L20=NΦ=IL2
(4)
式中:N为线圈匝数;Φ为单匝线圈的磁通量;L2[19]可表达为
(5)
μ0为真空磁导率,rc为定子线圈半径,ra为电枢半径,f为电感修正系数,
(6)
l为线圈长度;K为计算动态电感时的体积修正系数,
(7)
假定磁感应强度在空间内均匀分布[13],因此空间内的磁感应强度B为
(8)
式中:S为定子线圈与电枢间空腔的剖面积。
在磁通压缩的第2阶段,炸药爆炸,电枢在爆轰压力作用下向外膨胀,此时作用在电枢上的有向外的爆轰压力以及向内的磁压,磁压力模型[20]为
(9)
式中:θ为电枢膨胀角,即电枢向外膨胀时与轴线的夹角,如图4所示。在炸药爆轰的初始时刻,θ=0°。
4、各国应通过下述行动表明其致力于加强核安保的信心:参加国际同行评审,宣布核材料总量,承诺自愿共享最佳实践以及支持加强国际原子能机构在核安保领域的作用。

图4 FCG作用过程Fig.4 Process of FCG
电枢在爆轰压力和磁压共同作用下的运动方程为
(10)
式中:mi、vi和si分别为第i个电枢微元的质量、速度和面积;pdi和pyi分别为第i个电枢微元受到的爆轰压力和电磁力。
磁通压缩的第2阶段,开关S2闭合,电容器被短路,FCG作为供能源,此时的电路方程为
(11)
式中:α为磁通损耗系数,根据试验结果来拟合,一般取0.7~0.97。由于药型罩装置的电感远小于FCG电感,为了简化模型,不考虑药型罩的电感变化,且利用修正系数来近似替代电阻的热效应,动态电阻Rc=cR,c为修正系数[21]。将式(11)积分,即可得磁通压缩阶段的电流表达式:
(12)
1.4 压垮速度计算
记炸药1的长度为l1,炸药2的长度为l2,中间的间隔为l3,炸药1开始爆轰的时刻ts=(l1+l3)/D,此时药型罩可能已经在电磁力的作用下开始压垮,假定爆轰波速度无衰减,爆轰波追赶上压垮微元时,微元的运动距离为h1,此时对应的时刻即为爆轰压力与电磁力共同压垮药型罩的时刻:
(13)
式中:x为该微元距离顶端微元的轴向距离。药型罩微元的运动方程为
(14)

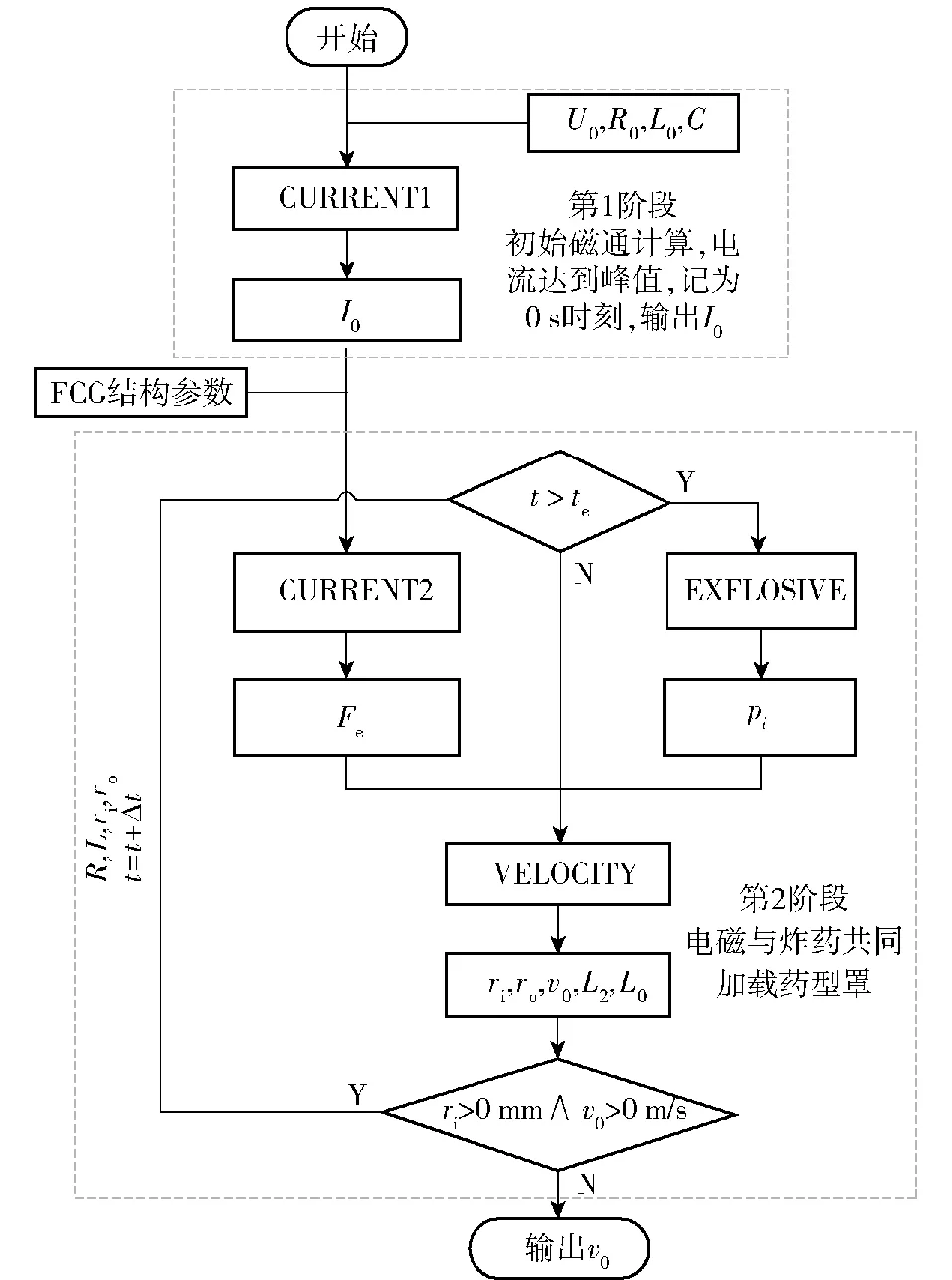
图5 计算联合加载下药型罩压垮速度流程图Fig.5 Flow chart of calculating the collapse velocity of the liner under combined loading
图5中,CURRENT1、CURRENT2、EXPLOSIVE、VELOCITY为自编的计算程序,根据式(1)~式(14)编写,输入初始的电压U0、电阻R0以及电感L0后,程序CURRENT1计算出加载第1阶段的峰值电流I0,输入至CURRENT2中,并且以初始FCG参数为初始输入条件,计算得到t时刻的电流值,进而求得作用在微元上的电磁力Fe。同时判断爆轰波是否传递至罩微元,若t>te,则由EXPLOSIVE计算出作用在罩微元上的爆轰压力pi,与电磁力Fe共同输入至VELOCITY程序中,求解t时刻微元新的位置(ri,ro)以及此时的压垮速度v0,反之则电磁力Fe单独加载药型罩。接着将得到的新的电阻电感以及微元位置反馈到下一步的计算中,作为下一个时间步的输入条件,依次循环直到计算结束。循环是否结束的判断依据是微元是否运动至轴线处(ri>0 m)且压垮速度是否大于0 m/s (v0>0 m/s)。当ri≥0 m 时,微元正常压垮至轴线处发生碰撞,输出此时刻的压垮速度即为在轴线处碰撞的压垮速度v0;当v0≤0 m/s时,说明电磁力太小不能克服材料的屈服应力导致运动停止,计算结束,输出压垮速度v0=0 m/s,以及此刻的微元位置。
1.5 射流成型理论
将坐标系建立在碰撞点Q上,从驻点坐标系来看药型罩的压垮过程,可以看见药型罩沿着母线方向向轴线压垮,记地球坐标系下的压垮速度为v0,驻点移动速度为v1,驻点坐标系下的压垮速度为v2,v0、v1和v2的关系如图6所示。图6中η为联合加载下药型罩微元的抛射角,可由其定义来计算。
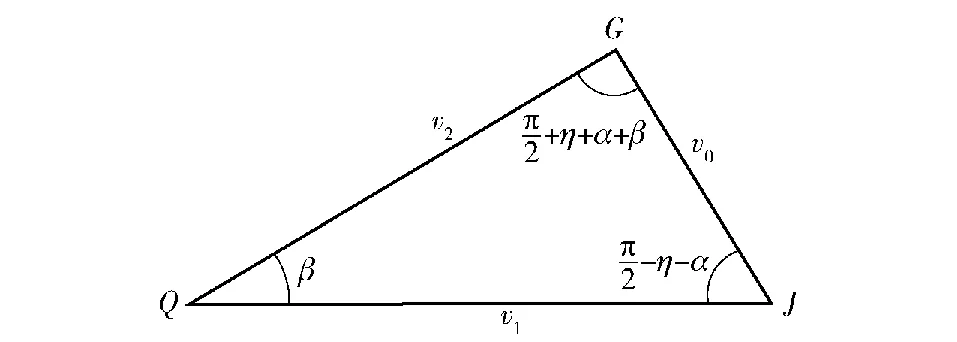
图6 驻点坐标系下的速度关系Fig.6 Velocity diagram in stationary point coordinate system
展示的速度之间的夹角由几何关系得到,各个速度之间的关系由正弦定理得到:
(15)
根据伯努利方程以及电磁加载特性[16],联合加载下射流和杵体的表达式为
(16)
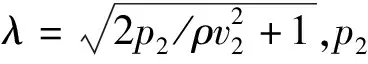
2 联合加载下药型罩形成射流分析
以φ56 mm装药为例,对联合加载进行计算分析。将原装药结构用于联合加载,φ56 mm装药结构如图7[21]所示,外径为56 mm,装药高度73.3 mm,药型罩壁厚为1 mm,锥角为60°,所使用的炸药为无壳8701,装药质量203 g,装药密度1.713 g/cm3,其爆速为7 980 m/s。
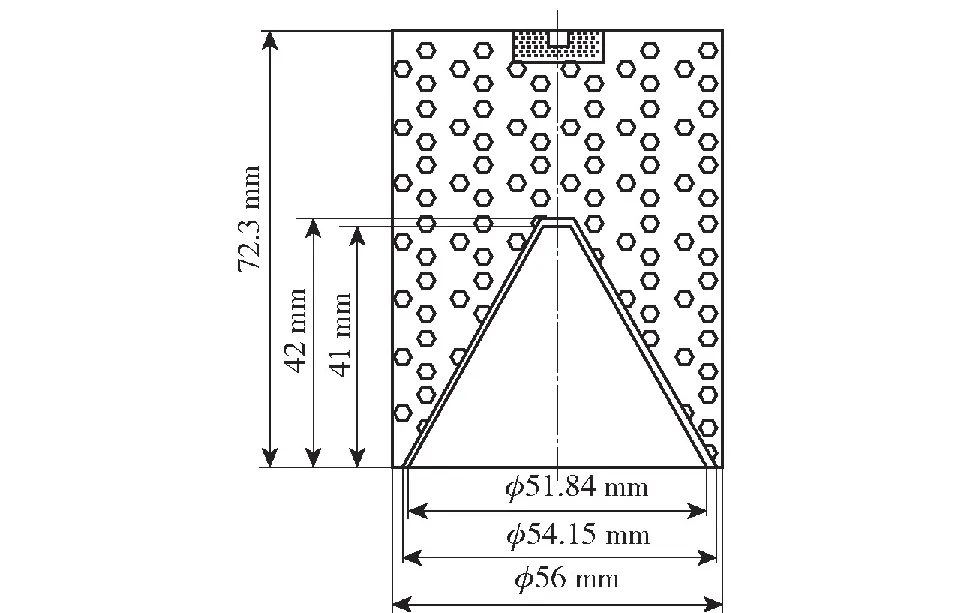
图7 φ56 mm聚能装药结构[21]Fig.7 φ56 mm shaped charge structure[21]
联合加载结构如图8所示,将基准装药分为炸药1和炸药2两部分,装药直径保持不变,都为56 mm,对应长度l1=20 mm、l2=53.3 mm,药型罩结构保持一致,电枢直径ra=31 mm,厚度为3 mm,定子线圈的缠绕半径rc=50 mm,选取导线直径ds=2 mm,因此线圈的匝数N=l1/ds=10。给定初始电路参数为加载电压U=20 kV,电容C=50 μF,连接导线电阻R1=0.1 mΩ,电感L1=0.1 μH,经计算FCG的电阻和电感分别为R2=2.2 mΩ、L2=4.1 μH,负载的电阻和电感分别为R3=0.01 mΩ、L1=9.4 nH。可以看出,相较于连接导线,FCG的电阻电感较大,负载的电阻电感可以忽略不计,在加载条件不变情况下,FCG的结构是影响加载电流的关键。
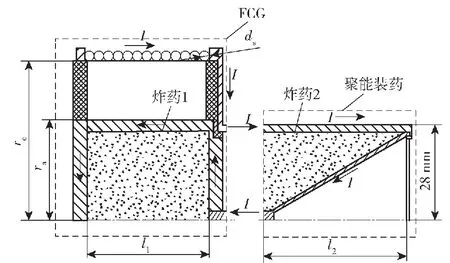
图8 联合加载装药结构Fig.8 Charge structure under combined loading
动态电阻的修正系数取5.7[21],忽略磁通损耗,在上述加载结构以及条件下,第1阶段加载的电流峰值为66.5 kA。到达电流峰值后,闭合开关S2短路电容器,同时引爆炸药,开始爆磁压缩阶段。记此时的时刻为0 μs时刻,磁通压缩阶段的电流以及FCG的电感变化如图9所示。在炸药爆轰的初始阶段,电枢的膨胀速度较低,电感变化较慢且减小的幅度较小,故炸药能量对电磁能的转化较慢,在10 μs前电流增加缓慢。随着FCG电感不断减小,电流增加速率变快,在14 μs时,FCG电感减小到最小值时,电流增大到最大值,图9中所示电流峰值为 1 739.6 kA。理想情况下,FCG电感减小到无限接近于0 μH,随后开始加载第3阶段,FCG中存储的电磁能对电路放电,电流不断减小,直到加载结束。
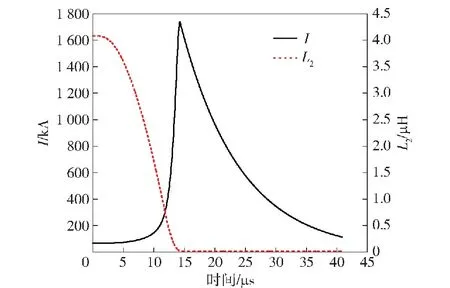
图9 磁通压缩阶段电流以及FCG电感变化Fig.9 Current and FCG inductance changes in the magnetic flux compression stage
取药型罩微元长度为1 mm,共42个微元,由药型罩的顶端至底端依次编号为1~42,药型罩在炸药加载和电磁炸药联合加载下的压垮速度和形成的射流速度分别如图10和图11所示,药型罩微元在联合加载下压垮至轴线的时间如图12所示。
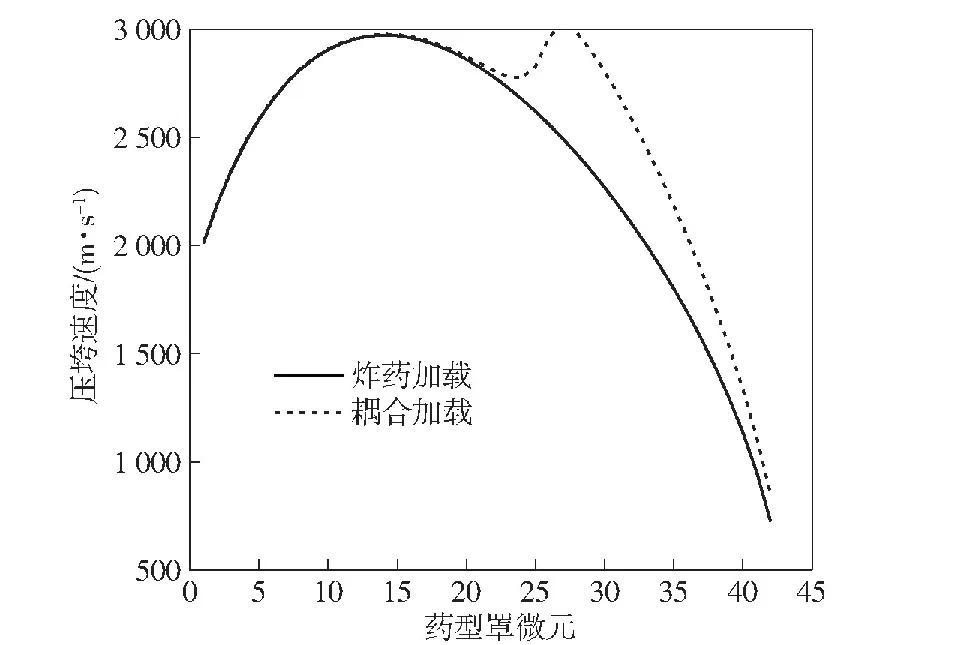
图10 不同加载方式下压垮速度对比Fig.10 Comparison of collapse velocities of different loading methods
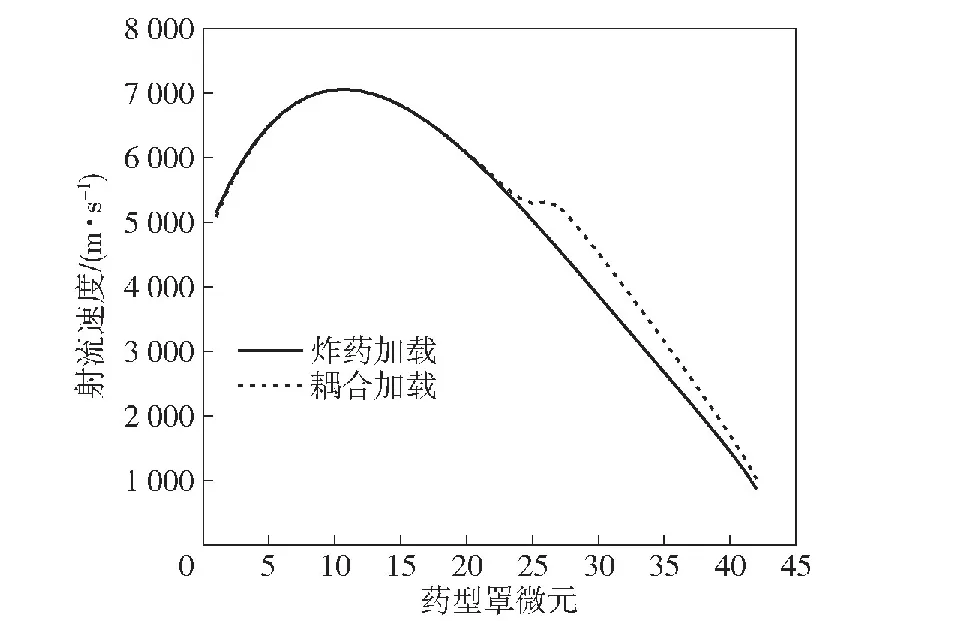
图11 不同加载方式下射流速度对比Fig.11 Comparison of jet velocities of different loading methods
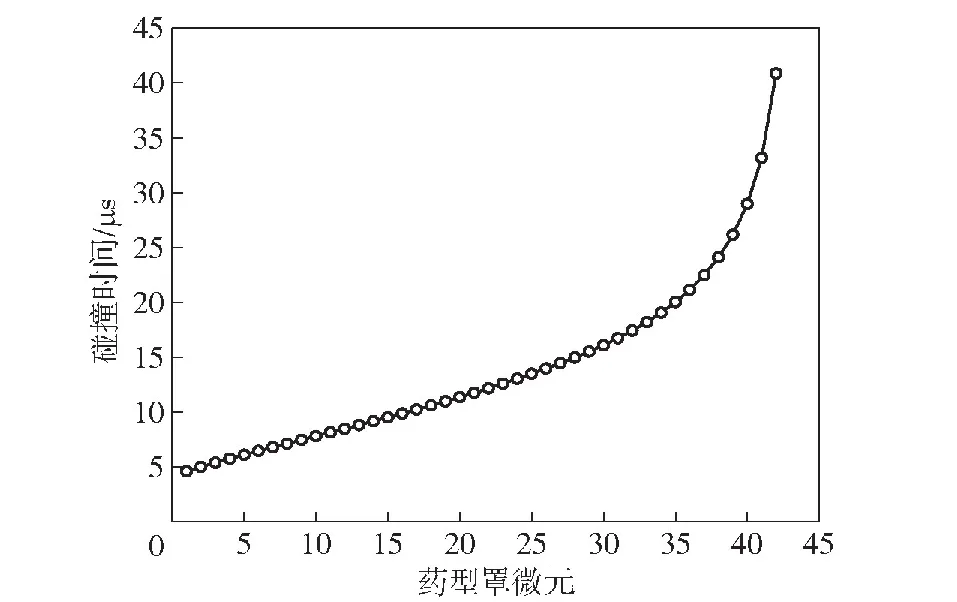
图12 微元压垮至轴线时间Fig.12 Time of elements collapsing to the axis
两种加载方式下的头部压垮速度和射流速度的变化趋势几乎一致,由图12所示,药型罩头部微元压垮至轴线的时刻在10 μs之前,而由图9可见,在10 μs之前电流较小,在压垮过程中作用在微元上的电磁力远小于爆轰力,电磁能未能完全作用于微元上,电磁力对头部微元的压垮速度的影响可忽略不计,故联合加载下头部微元的压垮速度和射流速度与炸药加载几乎一致。对于较靠后的微元,在压垮过程中,电磁力较大,在微元压垮至轴线前,大部分电磁能已经作用在微元上,故联合加载下的微元压垮速度和射流速度要高于炸药加载。
经计算,炸药加载下药型罩形成射流的动能为116 kJ,8701炸药单位体积的能量为9.5 J/mm3,故炸药总能量为1 373 kJ,对炸药能量的利用率为8.4%。在上述结构的联合加载下,射流动能为139 kJ,初始电容器的能量为10 kJ,相较于炸药能量可以忽略不计,因此联合加载下射流动能提高了19.8%,对炸药的能量利用率为10.1%,相对提高了20.2%。
3 联合加载时序对射流成型的影响
电磁能与炸药的联合加载是涉及电场、磁场、炸药爆轰的复杂过程,药型罩结构、装药结构、初始加载能量、加载时序等因素都会影响射流的成型状态,为研究联合加载下射流的成型机制,需要对各影响因素进行分析,这里选择对联合加载时序对射流成型的影响进行分析。
在上述计算中,由于药型罩头部附近微元的压垮时间与电流峰值时间未联合,头部微元速度相较于传统加载无明显提升。为了提高联合加载下药型罩头部微元的压垮速度以及射流速度,需要对联合加载时序进行调整,本文提出两种方案,一是通过改变联合加载结构,减小电流上升时间,二是将炸药2延时爆轰。下面分别对这两种优化方案下的射流成型进行计算。
3.1 减小电流上升时间
由式(11)可知,电流上升速率与FCG电感变化相关,而电感变化速率,取决于炸药能量、爆速、电枢厚度以及电枢和线圈的半径,这里通过只改变线圈缠绕半径,即rc的大小来改变电流上升时间。计算算例以及电流计算结果如表1所示,表1中下标0表示加载0 μs时刻的值,tu为电流上升时间,Imax为电流峰值,加载阶段的电流如图13所示。随着线圈缠绕半径的减小,FCG的初始电阻和电感都相对减小,在电容器电压和电容不变的情况下,第1阶段的电流峰值会随之增大。由于定子线圈的半径减小,电枢膨胀时间缩短,因此磁通压缩阶段的电流上升时间减小,但由于FCG初始电感的减小,导致FCG的电感在电路总电感中比重较小,因此放大后的电流峰值会相对减小。
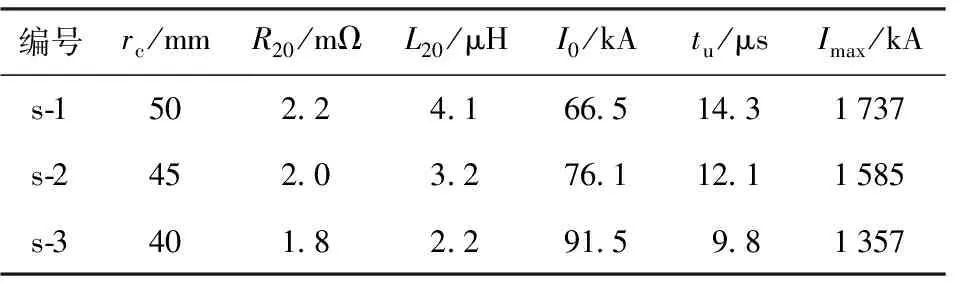
表1 计算算例Table 1 Numerical examples

图13 不同算例的电流比较Fig.13 Current comparison of different examples
随后计算了微元的压垮速度和射流速度,其中压垮速度以及第10、第20、第30和第40个微元的压垮速度对比如图14和图15所示,算例s-0为炸药加载。由图14可以看出,3种算例下,联合加载下药型罩微元的头部的压垮速度与炸药加载几乎一致,而随着微元位置的后移,结合图15,在第10个微元处,算例s-3的压垮速度最先开始有明显的增大,随后在第15个微元处,算例s-2的压垮速度有明显增大。对于第20个微元,算例s-3的压垮速度最大而s-1的压垮速度最小,说明了随着电流上升时间的减小,电磁力对药型罩头部微元的加载作用增大,在微元压垮至轴线前,更多的电磁能作用于微元上,相较于算例s-0,电磁力使得更多药型罩微元的压垮速度增大。对于后续微元,如图15所示的第30 和第40个微元,压垮速度随着电流上升时间的减小先增加后减小,这是因为底端微元压垮至轴线前,绝大部分电磁能已经作用,而电流峰值的降低,导致作用于底端微元的电磁能量减少,故压垮速度降低。
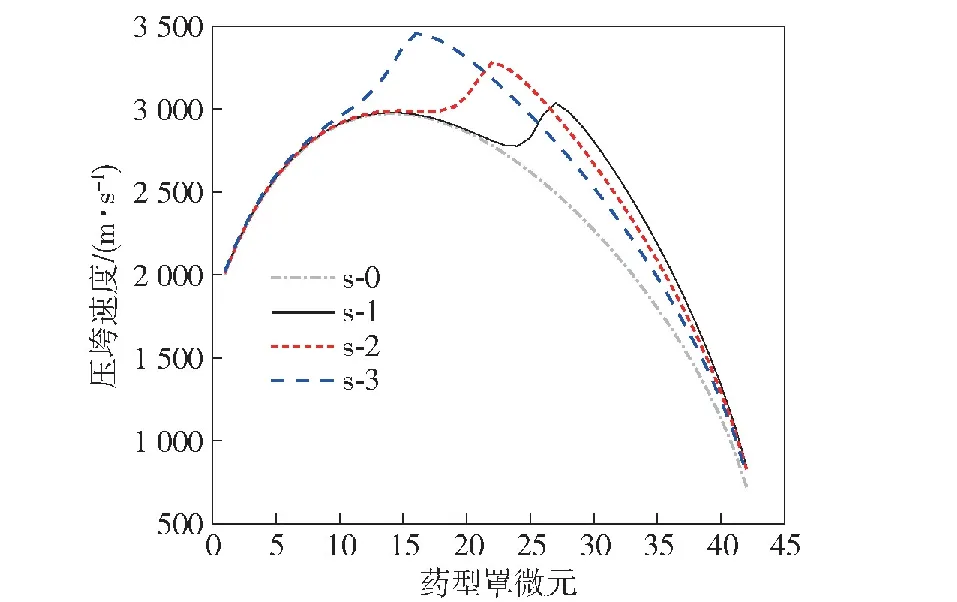
图14 不同算例的压垮速度对比Fig.14 Comparison of collapse velocities of different examples
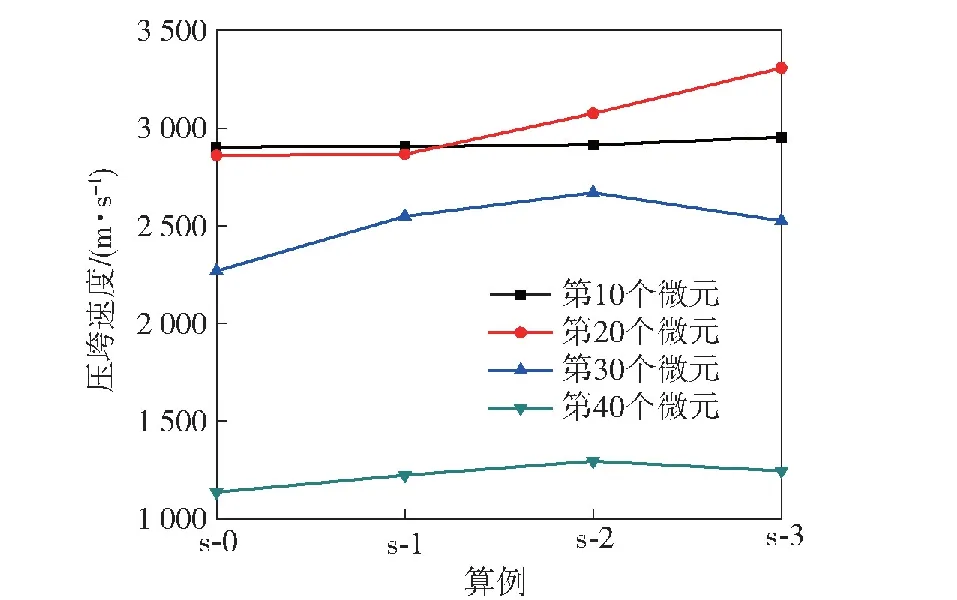
图15 不同微元的压垮速度对比Fig.15 Comparison of collapse velocities of different elements
图16展示了各微元形成的射流速度,图17为第10、第20、第30和第40个微元的射流速度对比,可以看出电流上升时间对射流速度的影响规律与压垮速度相同,由于压垮角的变化,射流速度对微元位置的变化相较于压垮速度出现了延迟,如第10个微元时,算例s-3的压垮速度相比于其他算例已经有明显的增大,但射流速度仍与其他算例几乎相同,在第13个微元时,才出现明显的增大。
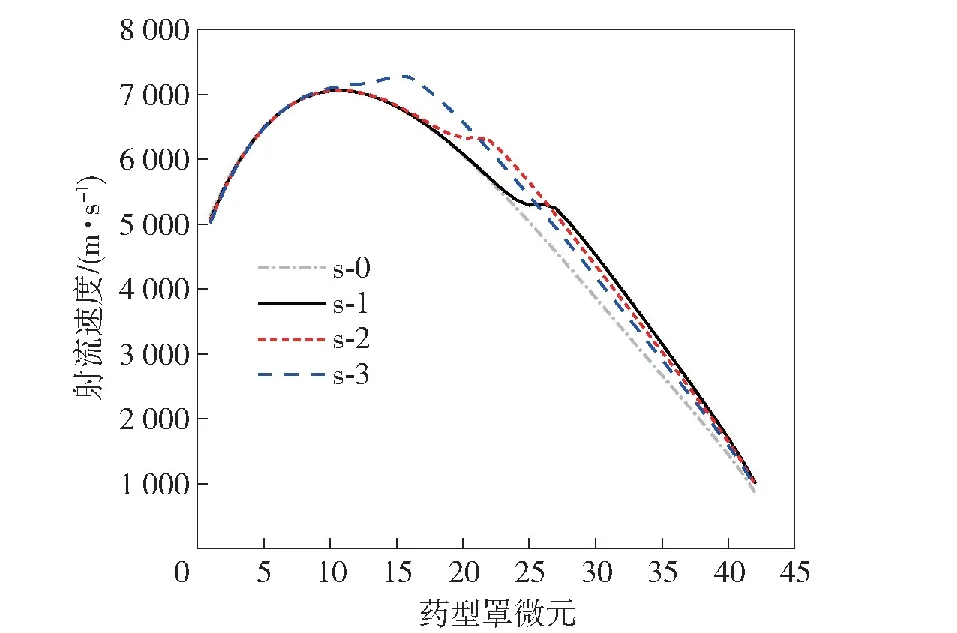
图16 不同算例的射流速度对比Fig.16 Comparison of jet velocities in different examples
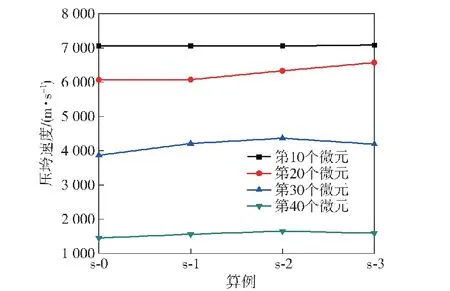
图17 不同微元的射流速度对比Fig.17 Comparison of jet velocities of different elements
算例s-2和s-3计算下的射流动能分别为 143 kJ 和144 kJ,3种算例下形成的射流动能都大于炸药加载下的射流动能,虽然随着电流上升时间的减小,药型罩顶端微元的速度有显著增加,但同时因为电流峰值的减小,相较于算例s-1,算例s-2和s-3的射流动能并没有显著增加。
3.2 炸药延时引爆
以算例s-1为基准,假定炸药2能延时起爆,由表1可知,算例s-2和算例s-3的电流上升时间相较与算例s-1分别减少了2.2 μs和4.5 μs,作为对比,假定炸药2分别相对于算例s-1延时起爆2.2 μs和 4.5 μs,记为s-2-1和s-3-1,相当于电流上升时间减小而电流峰值不变。计算得到的药型罩微元压垮速度和射流速度如图18和图19所示。算例s-2-1和s-3-1的药型罩的压垮速度和射流速度随微元的变化趋势与其对应的算例s-2和s-3一致,但数值上较大,说明了炸药2延时起爆后,电流集中的时间区间与药型罩顶端微元的压垮时间吻合较好,使得电磁能更多地作用于靠近药型罩顶端的微元。加载算例s-2-1和s-3-1的电流峰值分别大于算例s-2和s-3,所以微元的压垮速度和射流速度均增大。
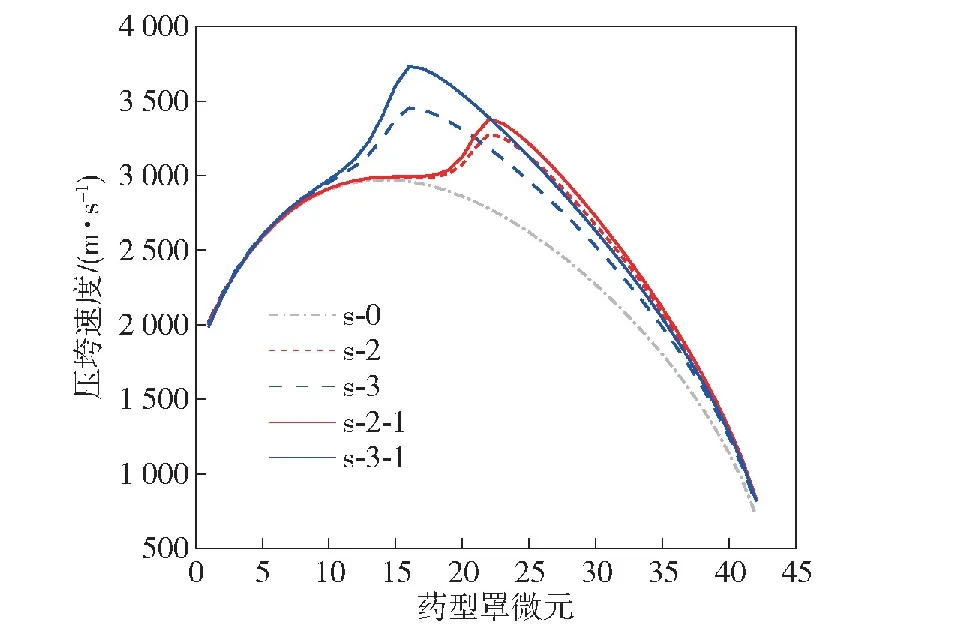
图18 压垮速度对比Fig.18 Comparison of collapse velocities

图19 射流速度对比Fig.19 Comparison of jet velocities
表2统计了所有算例下的射流动能以及对炸药的能量利用率,可以看出,相同炸药能量下,联合加载下形成的射流速度和动能都高于炸药加载,其中算例s-3-1,通过炸药延时起爆的方法,使得电流作用时间与炸药爆轰的作用时间联合更好,加载药型罩得到的射流动能最大(156 kJ),相对于炸药加载,射流动能提高了34.5%,对炸药的能量利用率相对提高了36%。

表2 射流动能和能量利用率Table 2 Kinetic energy and energy utilization rate of jet
4 结论
本文基于FCG原理,将原聚能装药结构中的圆柱部分装药设计为FCG结构,炸药1能量转换为电磁能后,与炸药2共同加载药型罩,同时建立了联合加载药型罩的理论模型,并通过理论计算了φ56 mm装药结构下联合加载的射流成型。得到主要结论如下:
1) 建立了电磁能与炸药联合加载药型罩的理论模型,理论计算结果表明,联合加载能够提高部分药型罩的压垮速度和射流速度,传统φ56 mm聚能装药形成的射流动能为116 kJ,联合加载下形成的射流动能为139 kJ,提高了19.8%,对炸药的能量利用率提高了20.2%。
2) 电磁能与炸药能量作用时序对射流成型有较大影响,在本文算例下,当电流的上升时间减小或者炸药爆轰作用时间延后时,联合加载下药型罩头部微元的压垮速度和射流速度增加,电磁能作用更多的药型罩微元,药型罩形成的射流动能相应增加。在本文算例中,通过改变电流与炸药的联合作用时序,形成射流动能最大为156 kJ,相较于传统炸药加载,提高了34.5%,对炸药的能量利用率提高了36%。

