基于滑动多周期FFT的调频引信抗扫频干扰方法
周文,郝新红,董二娃,陈彦君
(北京理工大学 机电动态控制重点实验室,北京 100081)
0 引言
引信作为一种弹药终端毁伤控制系统,直接决定了武器系统能否发挥出最佳毁伤效能,在现代战争及地区防御中占据重要地位[1]。作为引信的一个重要组成类型,调频引信由于其具有定距精度高、结构简单等特点,已在常规弹药中得到广泛应用[2]。而在日趋复杂的战场电磁环境中,诸如扫频干扰[3-4]等人为电子干扰手段对调频引信等无线电体制引信造成了巨大威胁[5-7]。
在无线电引信抗干扰方面,近些年已有学者展开了相关研究[8-14]。文献[8]提出基于熵特征与支持向量机的信号识别方法,通过提取检波信号的香农熵和奇异谱熵,结合支持向量机分类器,达到了较高的目标信号识别正确率;文献[10]利用调频信号在分数阶域的聚集性,提出一种基于分数阶傅里叶变换的调频引信定距方法。但上述方法所需计算量较大,对计算资源要求较高。文献[13]提出基于时序及相关检测的抗干扰方法,依据弹目接近过程中谐波峰值从高到低依序出现的规律,进行两路谐波时序逻辑判决,但在低信噪比条件下表现不够理想。
针对调频引信抗扫频干扰问题,本文提出一种滑动多周期快速傅里叶变换(FFT)谐波包络提取的处理方法。该方法通过多周期FFT相干积累抑制扫频干扰信号,并在相邻处理窗口间滑动更新一个调制周期长度的数据,降低差频信号不规则区带来的影响,能在扫频干扰下有效提取目标差频信号的谐波包络,明显优于调频引信单周期FFT谐波包络提取方法。
1 扫频干扰下调频引信失效机理
1.1 调频引信模型
调频引信的基本工作过程为:调制信号控制压控振荡器产生频率周期线性变化的射频信号,一路通过发射天线辐射出去,另一路送入本地混频器。接收天线接收到的回波信号通过低噪声放大器后与混频器中的本地参考信号进行混频处理,经模数转换器(ADC)采样后通过FFT提取差频的不同谐波包络,根据差频频率Δf的大小与距离的对应关系,完成预定炸高的设置。常见调频引信的主要工作过程如图1所示。
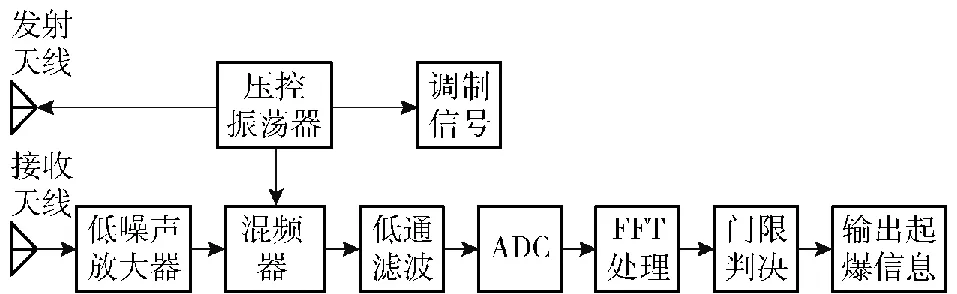
图1 调频引信工作原理Fig.1 Working mechanism of the FM fuze
以锯齿波线性调频引信为例,设发射信号幅值为At,初始频率为f0,调制周期为Tm,调制频率为fm,调制带宽为B,调频斜率为β,发射信号xt(t)可表示为

(1)
式中:n为当前时刻对应的周期数。
设真实目标回波经过的路径时延为τ,信号幅值为Ar,则回波信号xr(t)可表示为

(2)
忽略非规则区影响,经过混频器处理,单个调制周期内的差频信号xΔf(t)可表示为
(3)
对单个周期内的差频信号进行FFT处理,结果如图2所示,路径时延τ在单个周期内可视为常数,所得各次谐波系数的模可近似表示为

图2 单周期FFT处理结果Fig.2 Single-cycle FFT processing results

(4)
进一步可得距离分辨率ΔR为
(5)
根据式(4),差频频率随路径时延τ线性变化,在不同距离处,离对应差频频率最近的谐波系数幅值包络最大;对于单次谐波系数,其距离维包络表现为sinc函数,sinc函数零点为相关峰的峰值点,位于差频频率所对应弹目距离处。由式(5)可知,相关峰宽度与距离分辨率ΔR相关,其大小由发射信号调制带宽决定。
1.2 扫频干扰模型
干扰机扫频带宽能覆盖引信工作频带,扫频干扰信号的频率在扫频带宽内按一定规律步进,并在每个步进频点上驻留一定时间,当驻留频点进入引信工作带宽内,将对引信产生干扰效果[15-18]。如图3所示,干扰机采取扫频干扰方式,f为信号频率,t为当前时间,扫频初始频率为fj1,相邻频点间步进频率为Δfj,总扫频点数为G,每个频点的驻留时间为Δtj,扫频周期为Tj,则1个扫频周期内的干扰信号频率fj可表示为

图3 扫频干扰模型Fig.3 Frequency sweep jamming model
fj=fj1+(g-1)Δfj,g=1,2,…,G
(6)
进一步可得干扰信号xj(t):
xj(t)=Ajej(2πfjgt)·Pg(t)
(7)
(8)
1.3 扫频干扰下失效机理分析
一般来说,扫频干扰的驻留时间Δtj均大于引信信号调制周期,扫频干扰信号进入引信接收通道,并于本地参考信号混频后输出信号在1个调制周期内可表示为
(9)
Δfj=f0-fj+β(t-(n-1)Tm)
(10)
设低通滤波器的截止频率为fLP,经过低通滤波器后,能进入信号处理系统的干扰信号频带范围为
-fLP≤Δfj≤fLP
(11)
如图4所示,当干扰信号频率进入引信信号带宽内,干扰信号与本地参考信号混频后,所得差频信号可看作一段线性调频信号,有效长度由低通滤波器的截止频率fLP决定。

图4 扫频干扰下失效机理Fig.4 Failure mechanism under frequency sweeping jamming
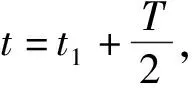

图5 干扰信号差频频谱Fig.5 Spectrum of beat signals under frequency sweeping jamming

(12)
式中:
(13)
为菲涅尔积分公式,积分限为
(14)
由图5可以看出,扫频干扰信号差频频谱覆盖整个引信信号处理带宽,由于干扰信号能量一般高于真实目标回波信号,当扫频干扰信号进入后,将对真实目标回波差频信号的频谱产生压制式遮盖效果,影响调频引信基于提取谐波包络特征的炸高判定效果,从而引起早炸或瞎火。
2 滑动多周期FFT处理方法
2.1 多周期FFT处理方法
利用发射信号在各个调制周期内具有强相干性,而干扰信号与本地参考信号非相干的特点,提出多周期FFT处理方法。考虑扫频干扰信号的影响,位于相关器两端的本地参考信号Sl(t)与混合接收信号Sr(t)可分别表示为
Sl(t)=xt(t)
(15)
Sr(t)=xr(t)+xj(t)
(16)
对Q个周期长度的相关器输出信号做傅里叶变换,各次谐波的系数由XQTm(f)表示:
(17)
进行变量替换t=t2+(q-1)Tm,根据积分的可加性,式(17)可改写为
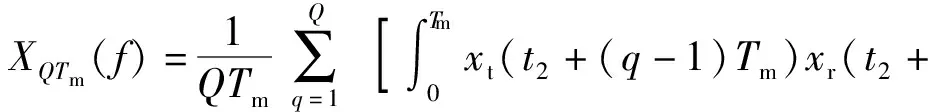
(18)
设式(18)中第1项为Xtr(f),由于发射信号与真实回波信号在各个调制周期内具有强相干性,Xtr(f)取模进一步简化为
(19)
设式(18)中第2项为Xtj(f),由于干扰信号与本地参考信号非相干,不同周期内的同一频率分量间存在相位差,因此在进行多周期积累时存在失配损失,Xtj(f)取模进一步简化为
(20)
当且仅当Q=1时,等号成立,Uq(f)表示第q个周期的差频信号频谱。
由以上分析可知,经过多周期FFT处理,真实目标回波差频信号分量的主要特征没有变化,固定次谐波的距离维包络依旧表现为sinc包络,但在频率轴方向上频率分辨率提高到单周期FFT处理结果的Q倍;干扰对应的差频分量在不同周期间存在相位失配,因此会抑制干扰效果。
2.2 滑动数据更新方法
考虑到在高速相对运动过程中,一个距离分辨单元内的信号调制周期数有限,若每次处理取多个周期数据,下一次处理数据全部更新,这会对谐波包络提取造成降采样的效果,将不利于后续判决处理。为了解决这个问题,借鉴短时傅里叶变换时频分析方法的思想,提出滑动多周期FFT谐波包络提取方法。
主要过程如图6所示,由于每个周期中的差频信号均存在一段非规则区,为保证每个数据处理窗口中非规则区带来的影响水平相同,因此将滑动更新数据的时间长度设置为调制周期的整数倍。为了得到更为细致的谐波包络,滑动更新数据的时间长度应尽可能短,因此,相邻处理窗口中原始数据滑动更新1个调制周期长度的数据较为合理。当Q=1时,滑动多周期FFT方法退化为传统单周期FFT方法。

图6 滑动多周期FFT处理流程Fig.6 Sliding multi-cycle FFT processing flow
设整个交会过程中采集的目标回波中频输出信号长度为Tall,进行Q个调制周期长度的滑动多周期FFT处理后(见图7),数据处理窗口总数i由式(21)决定:

i=Tall-Tm(Q-1)Tm

图7 滑动多周期FFT处理结果Fig.7 Sliding multi-cycle FFT processing results
(21)
式中:⎣·」表示向下取整。整个数据处理过程所得谐波频率矩阵X(f)可表示为
X(f)=[X1(f)X2(f)X3(f) …Xi(f)]
(22)
在Q取值较小时,可将数据处理窗口内的时延τ视为常数,此时Xi(f)可由式(19)近似表示。当Q值较大或弹目相对速度较大时,式(19)的准确性将变差。
由图7(a)可以看出,真实目标回波中频输出信号经过8个周期长度滑动多周期FFT处理后,所得时频矩阵的分布特征与式(19)描述一致,距离分辨单元在时频矩阵上线性分布,呈现出一个明显的时频脊。随着相对距离减小,对应差频频率随之减小,相邻分辨单元对应的谐波频率相差8次谐波;由图7(b)可以看出,在未施加扫频干扰的条件下,8个周期长度滑动多周期FFT处理所得距离维谐波包络依然为sinc函数的形状。
3 仿真及实验验证
3.1 仿真验证
为了验证上述分析,增加扫频干扰进行仿真验证,仿真参数设置如表1所示。

表1 仿真参数Table 1 Simulation parameters
对仿真所得差频数据分别进行单周期FFT及本文所提滑动多周期FFT方法处理,分别绘制仅目标信号作用下、仅干扰信号作用下及目标与干扰信号同时作用下的交会过程时频矩阵和距离维包络,所得结果如图8和图9所示。
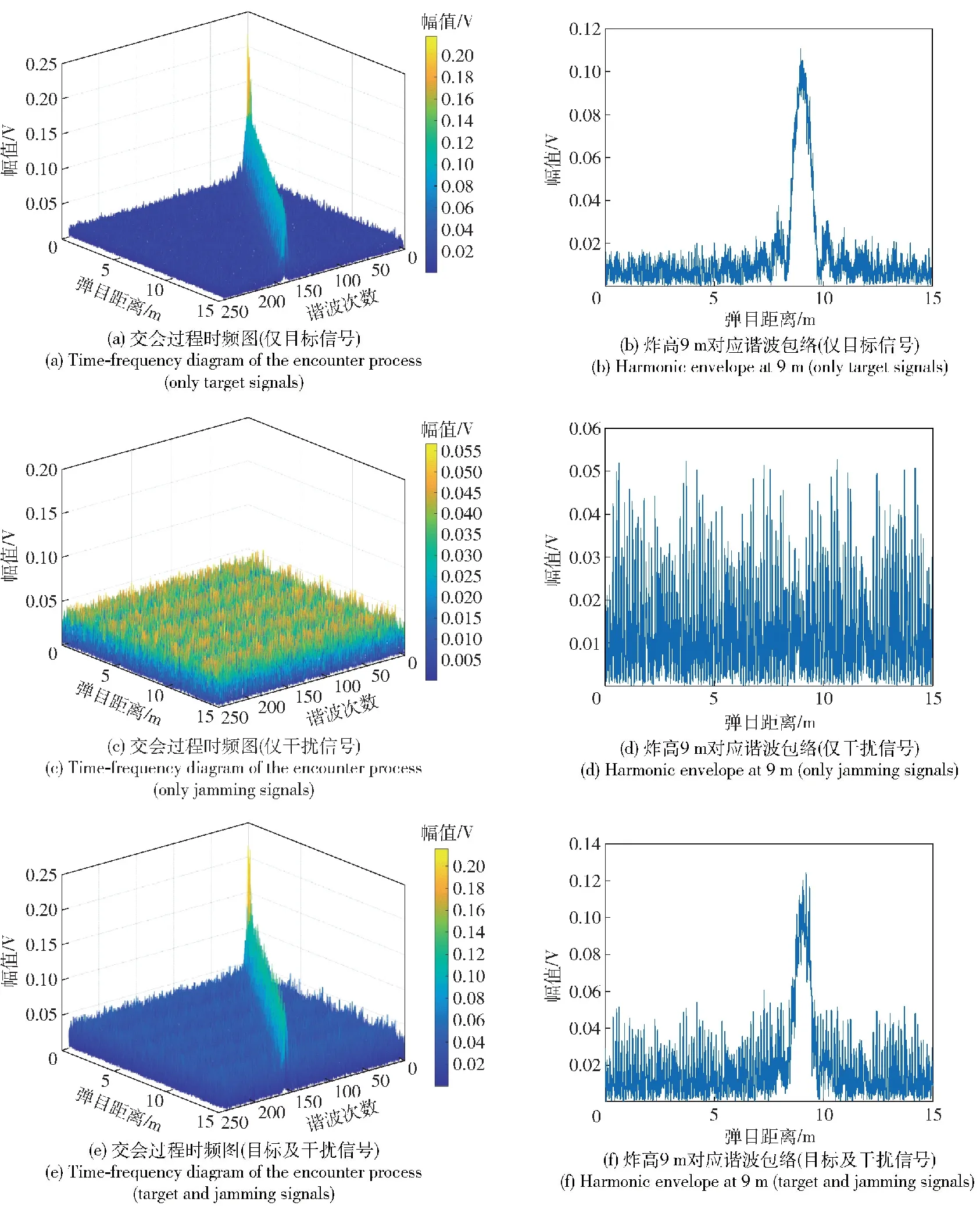
图9 仿真数据滑动多周期FFT处理结果Fig.9 Sliding multi-cycle FFT processing results of simulated data
由图8(a)及图8(b)可以看出,仅目标信号作用下,差频信号由单周期FFT处理后,所得时频脊较为明显,距离维相关峰高于背景噪声;由图9(a)及图9(b)可以看出,进行8个周期长度滑动多周期FFT处理后,背景噪声得到了有效抑制,距离维相关峰的sinc包络特征更加显著。
由图8(c)及图8(d)可以看出,仅干扰信号作用下,差频信号由单周期FFT处理后,全局时频分布中包含大量异常峰值,峰值大小高于目标信号相关峰水平;由图9(c)及图9(d)可以看出,进行8个周期长度滑动多周期FFT处理后,干扰信号带来的异常峰值已低于目标信号相关峰水平。
由图8(e)可以看出,在目标信号及干扰信号的同时作用下,由单周期FFT处理后所得时频矩阵,其各次谐波中均混入大量由干扰信号带来的虚假峰值,真实目标回波所对应的时频脊被遮盖;由图8(f)可以看出,9 m对应谐波包络中真实目标相关峰掩盖在干扰信号中,对门限判决产生不利影响。
由图9(e)可以看出,进行8个周期长度滑动多周期FFT处理后,时频矩阵中由干扰信号带来的虚假峰值被大幅压低,可以清楚观察到真实目标回波所对应的时频脊;由图9(f)可以看出,通过滑动多周期FFT有效压制干扰信号后,距离维谐波包络中再次出现明显的相关峰。
峰值旁瓣比(PSLR)是衡量无线电信号抗干扰能力的一项重要指标[19-20],其数值越小,表示抗干扰性能越好。为进一步进行抗干扰效果指标度量,采用PSLR对在不同JSR条件下不同周期长度滑动多周期FFT处理结果的抗干扰性能(见图10)进行表征:

图10 滑动多周期FFT处理后PSLR结果Fig.10 PSLR results of sliding multi-cycle FFT processing
(23)
式中:PPSLR为PSLR;Pside为最大旁瓣功率;Ppeak为峰值响应功率。
由图10可以看出:当JSR较低时(如JSR=9 dB),在一定范围内,随着周期数Q的增加,在不同JSR条件下的PSLR均有明显下降;当Q值较大时,PSLR下降幅度有限;当JSR较高时(如JSR=21 dB),随着周期数Q的增加,PSLR的改善幅度较为有限,当Q取值高于8时,PSLR没有得到明显改善。从前文分析可知,当Q取值过大,Q个周期内的回波数据相干性变差,会影响滑动多周期FFT方法的处理效果,根据仿真结果,建议周期数Q的取值范围为2~16。
Q的增大也会带来计算量的增加,对实时性会造成一定影响,如表2所示,给出了不同处理周期数Q对应的计算时间(基于美国Xilinx公司Spartan-6系列FPGA的测试结果)。一般来说,引信信号处理的延迟应控制在毫秒量级,因此,综合考虑最优抗干扰性能与实时性的平衡,本文选用Q值为8。

表2 不同周期数所需计算时间Table 2 Calculation time required for different cycles
3.2 实验验证
为了进一步验证基于公式推导及仿真分析的正确性,现基于某引信样机进行实测数据采集及分析。实验场景如图11所示。主要实验过程为:设置目标散射截面积(RCS)为1 m2的金属平板,运动平台从12 m运动到8 m位置处,交会速度1 m/s,采集交会过程引信差频输出信号。

图11 实验场景示意图Fig.11 Schematic diagram of the test setup
将采集的差频数据分别进行单周期FFT及本文所提滑动多周期FFT方法处理,提取并绘制交会过程时频矩阵及9 m炸高对应谐波的距离维包络,所得结果如图12和图13所示。

图12 实测数据单周期FFT处理结果Fig.12 Single-cycle FFT processing results of measured data

图13 实测数据滑动多周期FFT处理结果Fig.13 Sliding multi-cycle FFT processing results of measured data
由图12和图13可以看出:由单周期FFT处理后所提取的时频矩阵无法看出主要频率分量随距离的线性变化关系,相关峰不明显,低于由扫频干扰带来的干扰信号谱线高度。采用本文所提滑动多周期FFT处理方法,提取的时频分布图可以明显看出时频线性对应关系,并且9 m炸高谐波包络的相关峰特征明显,有利于下一级判决处理。
4 结论
为提高调频引信对抗扫频干扰的能力,本文在分析扫频干扰下调频引信失效机理的基础上,提出一种滑动多周期FFT处理方法,通过仿真及实测结果验证了该方法的有效性。得出的主要结论如下:
1) 扫频干扰信号能覆盖调频引信工作带宽,对真实目标回波差频信号的频谱产生压制效果,对目标判决造成不利影响。
2) 通过在数据处理窗口进行多周期FFT相参积累,可以实现对扫频干扰的有效抑制,PSLR得到显著改善。
3) 在相邻处理窗口中滑动更新部分数据,可以获得更为细致的距离维包络,有利于下一步目标判决处理。
4) 本文所提方法的算法复杂度低,能够满足引信的实时性要求。

