图论中若干经典问题

武育杰　王浩　王宏立　王晓

关键词：图论；四色问题；中国邮递员问题；哈密尔顿图

中图分类号：O157.5 文献标识码：A

文章编号：1009-3044（2023）14-0106-03

1 引言

图是一个具有二元代数结构特征的数学模型，由顶点集和边集构成，顶点表示研究对象，边表示研究对象之间的关系。凡是涉及研究对象及其关系的问题都可以用“图”来建立其拓扑数学结构。图论作为理论工具，在复杂网络系统、多智能体、分子结构和能量、生物基因谱分析、大数据分析以及社交网络等诸多领域中都有着广泛的应用。

图论作为数学学科的一个分支，已经有200余年的历史。公认的图论第一篇论文是由瑞士数学家欧拉在1736 发表的关于哥尼斯堡七桥问题的论文[1]。在哥尼斯堡七桥问题中，将各个独立的陆地区域视为顶点，每一座桥视为连接两个顶点的边，便构造了一个既简洁又直观的图。1847年Kirchhoff运用图论作为工具，成功地解决了电路理论中求解联立方程的问题，引进了“树”的概念，树是图论也是计算机理论中最基本并且是应用最多的概念之一[1]。1857年Cayley 在有机化学领域利用图论中的树为工具，解决了计算饱和氢化物同分异构体的数目的问题，这使得图论在化学领域也发挥了重要作用。1936年，匈牙利数学家Konig出版了图论的第一部专著《有限图与无限图理论》，这是图论发展史上最重要的里程碑，它标志着图论已成为一个具有完整体系的数学分支[2]。

现实世界中许多问题都可以用图来描述其数学拓扑结构，通讯网、交通网、社团网、化学分子结构、生物基因图谱、大规模集成电路都可以用图来建立其数学模型框架。在理论研究上，图论主要分为结构图论、极值图论、代数图论、随机图论、拓扑图论等几个主要模块，这几个方面相互促进相互影响，共同促进图论的发展。

一个好的数学问题应该具有描述的简洁性、结论的出乎意料性、应用上的一般性。图论中的四色问题、欧拉图问题和哈密尔顿问题就完整地具备这些特征。由四色问题衍生出图的着色理论，已成为结构图论中最经典的部分[3]；中国邮递员问题来源于欧拉图问题，是中国学者研究图论的典型结果之一[4]；哈密尔顿图问题也称为周游世界问题，是一个经典的NP-困难问题，对NP问题的研究起到了重要的促进作用[5]。通过对图论中一些经典问题的起源、发展及影响的概述，可以促进图论知识的普及，吸引更多研究者深入研究图论理论及其应用。

2 图论的起源——哥尼斯堡七桥问题

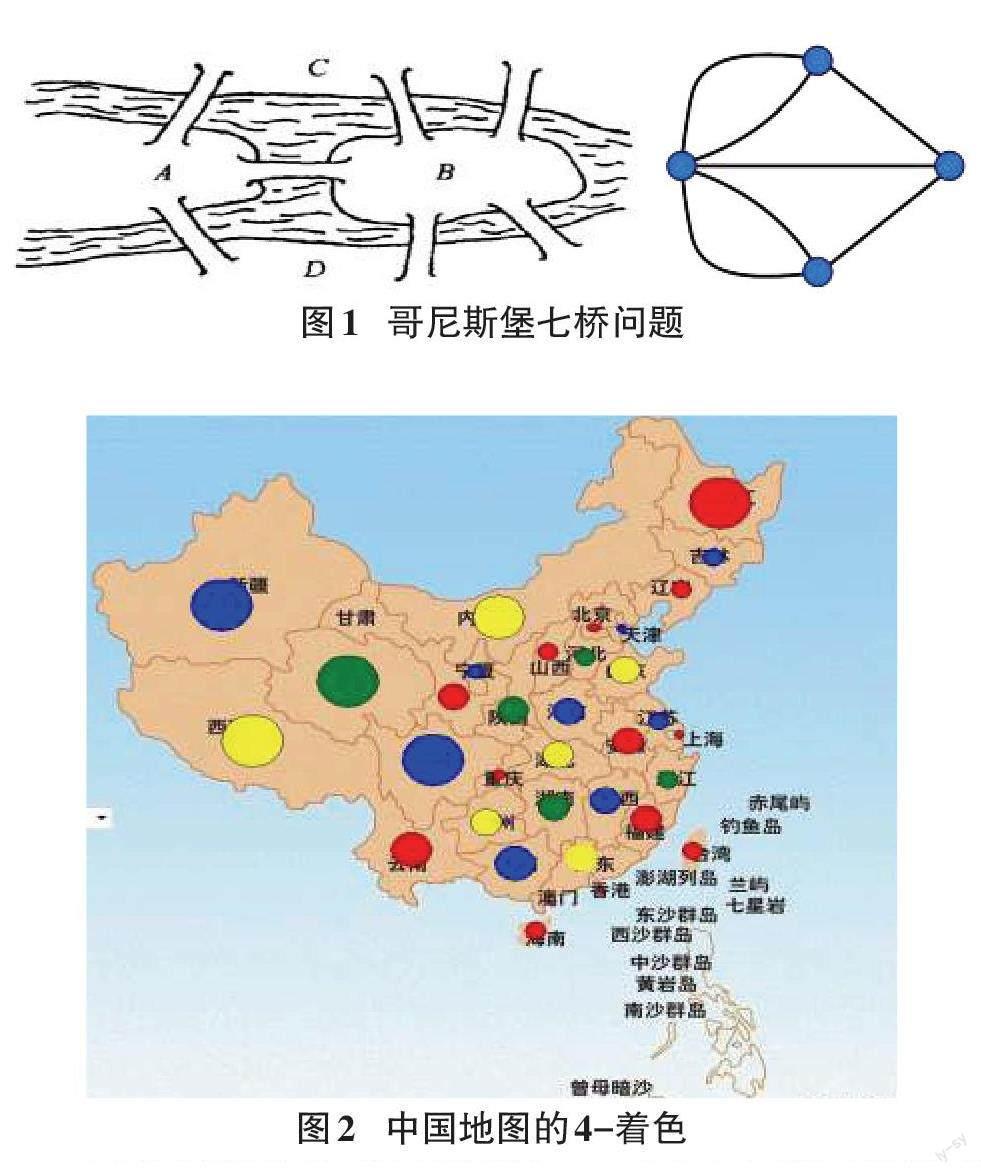
十八世纪的哥尼斯堡（現为俄罗斯的加里宁格勒），普列戈利亚河横穿其中，河上有七座桥，连接着A、B、C、D四块陆地，如图1所示。当地流传着一个著名的游戏谜题：能否从某块陆地出发，恰好把每座桥走一次，最后又回到原地？1735年几名大学生给当时的数学家欧拉写信，请教这个问题。一年之后，欧拉证明了哥尼斯堡七桥问题是无解的，并引入了图的概念，由此开创了图论这一新的数学分支。

欧拉将A、B、C、D四块陆地看作顶点，连接它们的桥看作边，七桥问题就转化为图1中右边的图是否有经过每一条边恰好一次的回路的问题。这样的回路称为欧拉回路，欧拉证明了图论中最古老的定理（欧拉定理）：无奇度顶点的连通图存在欧拉回路且可分解成边不交的圈。同时，欧拉处理七桥问题的方法也蕴含着拓扑学的思想，拓扑学只关注图形形状的连接性，而并不关注自身的具体的大小和距离。交通网络图、通信网络图、社交网络图等都是以图为基本结构来建立现实问题的数学拓扑模型。

山东师范大学的管梅谷教授在20世纪60年代提出一个运筹学问题：邮递员每天从邮局出发，走遍该地区所有的街道再返回邮局，他如何安排送信路线可以使所走的总路程最短？这个问题被称为中国邮递员问题，其数学描述为：在赋权图中找一条回路，使得过每条边至少一次，且边的权之和最小，即为带权最优欧拉回路问题。管梅谷给出了奇偶点图上作业法，求解中国邮递员问题。1985年Edmonds给出了中国邮递员问题的多项式算法[6]。

由欧拉定理可知欧拉图的边可以分解为边不交的圈，但是最少可以分解成多少个边不交的圈呢？Hajos曾给出猜想（被称为Hajos猜想）：n个顶点的欧拉图至多可以分解为n/2个边不交的圈[7]。1966年，Erd?s、Goodman和Posa将此猜想弱化，猜想存在常数c使得n个顶点的欧拉图可分解成cn个边不交的圈。这两个猜想被Pyber认为是“out of reach at present”。

认哥尼斯堡七桥问题为起源，欧拉引出了“图”这一数学模型结构，构建了图论的雏形。随着中国邮递员问题、欧拉图的圈分解问题等的出现，进一步促进了图论的发展。

3 图论发展的动力——四色问题

四色问题曾和费马猜想（1994年已由英国数学家证明，被称为费马大定理）、哥德巴赫猜想被称为世界三大数学猜想。1852 年Morgan 教授的一位学生问他，能否证明：只需四种颜色就可以给任意地图的每个国家着色，使得任意有共同边界的国家所着的颜色不同。把地图看作一个平面图，国界看作是边，不同国界的相交处看作是顶点，每个国家的区域就是面，则上述问题就是：任意一个平面图最多用四种颜色给每个面着色，就可以使得有任何有公共边的面所着的颜色都不同。如图2，用4种颜色就可以把中国地图各个相邻的省份区分开。

1872年，英国数学家Cayley正式向伦敦数学学会提出了四色问题。自此以后，四色问题逐渐成为世界数学界关注的研究对象，吸引了一批优秀的数学家不断地进行探索。一百多年来，这个看似简单的问题，却让许多一流的数学家“折戟沉沙”。后人评价德国著名数学家Minkowski（曾是爱因斯坦的老师），最让他尴尬的不是他曾骂爱因斯坦是“懒虫”，而是他被四色问题挂在了黑板上。

1878年到1880年之间，数学家Kempe和Tait先后发表了关于四色问题的论文，宣布四色问题已获得证明。大家都认为四色问题从此也就解决了，然而十年后，人们却发现这两人的证明都是错误的。1890年Heawood给出了Kempe证明中的一个反例（即为著名的Heawood 图），从而推翻他的证明，并且利用Heawood的方法却可以很容易就得到平面图的5-色定理。Tait证明的错误之处是他认为3-正则且3-连通的平面是哈密尔顿图（有一个圈包含图中所有的顶点）。1946年，数学家Tutte给出了一个3-正则且3- 连通的平面图不是哈密尔顿图，从而彻底宣告了Tait 证明中的错误是无法修补的。虽然Kempe和Tait关于四色问题的证明是错误的，但是他们二人均为之后四色问题的证明奠定了基础，并为之后图论的发展做出了不可磨灭的贡献。

20世纪以后，数学家关于四色问题的探索基本上是沿着Kempe 的思路进行。1936 年，美國数学家Franklin证明了22个面以内的平面图都是4-可面着色的。沿用此思路，四色问题在1950年被改进到了35个面，随后又被改进到了50个面。1976年，美国数学家Appel和Haken与计算机专家Kock三人合作完成了四色问题的证明[8-9]，这也开创了利用计算机来证明数学重大问题的先河。1994年，Seymour在第22届国际数学家大会上做了1小时报告，报告的主题就是关于四色问题的证明。

给出Tait证明四色问题反例的数学家Tutte，一直致力于研究从纯粹数学的角度来证明四色问题，希望找到纯推理的方法来证明。为此，Tutte创立了整数流理论[10]，从更大的框架内来研究四色问题。Tutte提出了三个整数流猜想，形成了整数流研究的核心问题。目前，整数流理论已成为图论研究的前沿问题之一。

4 图论的NP-困难问题——哈密尔顿图

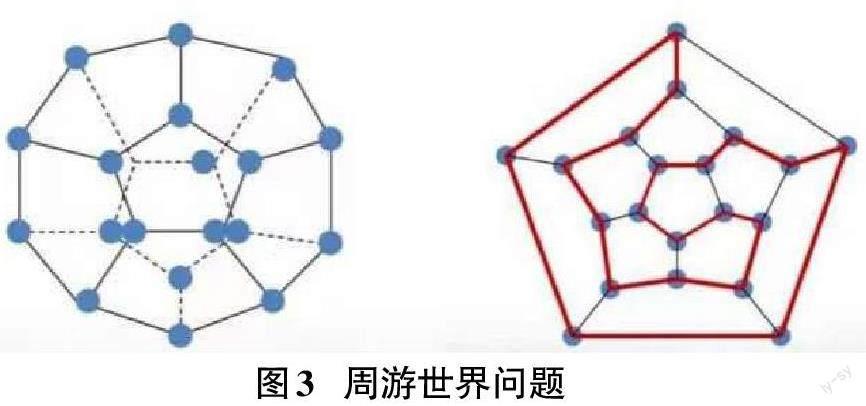
1856年爱尔兰数学家哈密尔顿（他也是第一个给出复数的代数表示的数学家）设计了一个游戏：给定一个十二面体（如图3所示），每个点代表一个城市，每条棱代表两个城市之间的一条路，是否存在从某一城市出发，经过每座城市恰好一次，最后又回到出发点？此问题也称为周游世界问题。十二面体的20个点的拓扑结构可以用图3中右图的平面图来表示，周游世界问题是有满足条件的走法的，即图中存在一个圈恰好包含每个顶点一次，这样的圈称为哈密尔顿圈，含有哈密尔顿圈的图称为哈密尔顿图。

更一般化的周游世界问题，或者称为旅行商问题，即一个旅行商从公司出发，访问若干指定城市，最后返回公司，要求设计最优旅行路线（行程最短或费用最小）。数学抽象描述为：在赋权图中找一条回路使得过每个点恰好一次且边的权之和最小，即寻找赋权最优哈密顿圈[5]。

不同于欧拉图，目前还没有一个判定图是哈密尔顿图的非平凡的等价条件，这也是图论中最重要的未解决问题之一。1952年，Dirac给出了判定哈密尔顿图的度型条件；1960年，Ore给出了改进的度型条件；1972年，Chvátal给出了判定哈密尔顿图的度序列条件；1976年Bondy和Chvátal给出了判定哈密尔顿图的闭包条件[1]。

从算法角度看，判定图的哈密尔顿性是NP-困难的。研究世纪猜想——NP问题，哈密尔顿图即为一个很好的突破口。通常判定一个图是否含有哈密顿圈都是用穷举的方法。Rubin利用推演的方法给出了一个可优化的搜索步骤寻找图中的哈密尔顿圈，An?gluin和Valiant利用概率方法设计了一种寻找哈密尔顿圈的非常有用的方法。

从应用的角度看，从工业铺路到农业灌溉，从航空路线到海底侦察，从国家的发展到公司的运输都要用到哈密顿图的基础数学模型结构。对哈密尔顿图的研究已经显得越来越重要，利用哈密尔顿图的研究结果，可以大大提高工作的效率和节约发展成本，为可持续发展提供重要支持。

5 结束语

国内著名图论学者范更华教授曾讲过，以蒸汽机为标志的工业革命促进了以微积分为基础的连续数学的发展，以计算机为标志的信息革命将极大地促进离散数学的发展，而图论则是离散数学最主要的分支之一。现实世界中许多问题都可以用图来描述其数学拓扑结构，四色问题、中国邮递员问题和周游世界问题都是图论中的经典问题，在图论学科的发展过程中起着至关重要的作用。综述图论中经典问题的发展历史，可促进图论知识的普及，吸引更多研究者深入研究图论理论知识及其在现实中的应用。