浅谈图论与线性代数的联系
孙燕玲
(济南大学 泉城学院基础教学部,山东 蓬莱 265600)
浅谈图论与线性代数的联系
孙燕玲
(济南大学 泉城学院基础教学部,山东 蓬莱 265600)
图论是数学的一个重要分支,它的应用也十分广泛,与此同时它与其他的数学分支也有着重要的联系,本文主要讨论图论与线性代数的联系,我们将运用线性代数中的内容解决图论中的问题。
图论;邻接矩阵;线性代数
1引言
图论在近二十年来发展十分迅速,应用也比较广泛,主要是研究图的相关性质。图论是指由点和点与点之间的连线所形成的图形,将这些图形中的点和线赋予一些特定的意义,用这些点和线来描述事物间的关系,点指的是事物,线代表事物间的关系。
文章所涉及的只是图论中的一些基本概念和理论,在方法上应用线性代数中的内容来研究图的一些性质。用线性代数中矩阵表示一个图的各种关系,不仅是给出图的一种表示方法,而且可以充分利用矩阵代数中的各种运算,来研究图的结构特征及性质,且便于计算机处理。用矩阵表示图,必须首先将图的顶点、边等分别按照某种顺序排列,然后并按照这种顺序依次给定惟一标号,使其成为标号图,最后给出其矩阵表示。用矩阵表示一个图的各种关系,不仅是给出图的一种表示方法,而且可以充分利用矩阵代数中的各种运算,来研究图的结构特征及性质,这样便于用计算机处理图。
2利用邻接矩阵的乘法解决图论中路径问题
定义1设G=〈V,E〉是一个简单有向图,V={v1,v2…,vn}A(G)=(aij)n×n,其中:
称A(G)为G的邻接矩阵。简记为A。


注:用A的幂求不同长度通路(回路)的总数,下面我们通过一个例子来说明相应的问题。
例1 设G=〈V,E〉为简单有向图,如下图所示,写出G的邻接矩阵A,算出A2,A3,A4且确定v1到v2有多少条长度为3的路?v1到v3有多少条长度为2的路?v2到自身长度为3和长度为4的回路各多少条?
解:邻接矩阵A和A2,A3,A4如下:




3利用行列式解决图论中生成树的问题
定义2设G=〈V,E〉是无向图,V={v1,v2…,vp}E={e1,e2…eq}M(G)=(mij)p×q

称M(G)为无向图G的完全关联矩阵。简记为M。
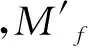

例2 求下面图形的所有生成树。
根据定义可以得出右图中的完全关联矩阵为
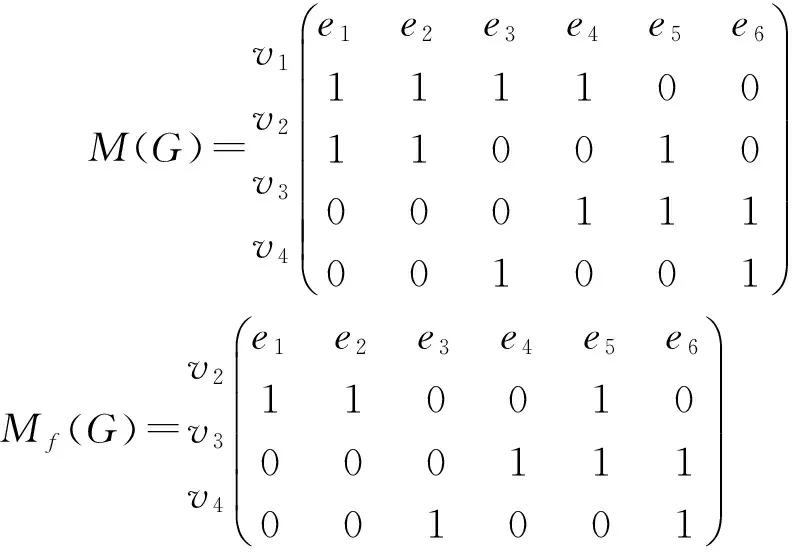
4用秩解决图论中图的连通性的问题
定理3若G为有向连通图,B为G的关联矩阵, 则秩(B)=n-1。
证:将关联矩阵B的各行全部加到第k行,则第k行为零向量。记新得到的矩阵为B′, 则秩(Bk)=秩(B′)=秩(B)=n-1。
定理4设Bk为有向图D的基本关联矩阵,且C={e1,e2…,ek}是D中的一回路,则回路C的各边对应的矩阵Bk的各列必线性相关.
证:设C由边e1,e2,…ek组成,C对应的关联矩阵B的各列向量为a1,a2,…ak,则可验证a1+a2+…ak=0,故a1,a2,…ak线性相关。
推论若有向图G的子图H含有回路,则H对应于任一基本关联矩阵Bk的列向量组线性相关。
将矩阵和图论联系起来,能够更简单的理解图论的知识,对于理解题目的涵义也有影响。将图论问题转化为矩阵问题,在前人总结的经验基础上进一步深化,将矩阵的知识运用恰当对于我们解决图论问题也比较便利,给我们提供了解决图论问题的另外一条思路,使得我们需要解决的问题得以简化。因此,研究图论和线性代数之间的关系意义重大。
[1]卜月华.图论及其应用[M].南京:东南大学出版社,2002.
[2]刘亚国.图论邻接矩阵的运用[J].沂州师范学院学报,2008,(4).
[3]贾进章,刘 进.基于邻接矩阵图的连通性判定性原则[J].2003,(2).
[责任编辑鲍艳]
DiscussionontheRelationbetweenGraphTheoryandLinearAlgebra
SUN Yan-ling
(CommonCoursesTeachingDepartmentofQuanzhouCollege,JinanUniversity,PenglaiShandong265600,China)
Graph theory is an important branch of mathematics and widely used, at the same time it has important connection with other branches of mathematics. This paper mainly discusses the relation between graph theory and linear algebra, and we will use contents in linear algebra to solve the problem in graph theory.
graph theory; adjacency matrix; linear algebra
2014-05-12
孙燕玲(1987-),女,山东蓬莱人,济南大学泉城学院基础教学部助教,硕士研究生,主要从事图论与组合优化研究。
O151.2
A
1009-9042(2014)06-0092-02

