基于多薄壁圆管套装假设的圆轴扭转切应力-变形量分析

张居敏，王 鹏，邓在京

（华中农业大学 工学院，湖北 武汉 430070）

受扭圆轴的切应力-变形量理论公式在材料力学、工程力学等力学课程中占有重要地位，也是教学重难点［1-4］.当前教材都采用楔形微体理论导出这些公式［5-9］，方法过于单一，过程有点抽象，初学者不易接受.

文 献［1-4］给出了楔形微体理论在实际教学中的具体教法建议，指出了平面假设在该理论中的核心性地位.文献［10］试图用能量法推导受扭圆轴的切应力-变形量理论公式，该方法理论价值高，但比较抽象、复杂，不便于课堂教学.

笔者以薄壁圆管的切应力-变形量理论及公式为基础，基于多个薄壁圆管套装假设，推导了厚壁圆管的切应力-变形量公式，并指出厚壁圆管的切应力-变形量公式完全适用于薄壁圆管，最后以薄壁圆管为例阐述了切应变γ角的物理含义及具体测量方法，为剪切胡克定律公式的正确性提供了实验验证方法 .研究结果有助于提升圆轴扭转理论的内在逻辑关系，有助于课堂教学.

文内涉及的所有轴和圆管，其材质及受力都与教材文献［5-9］中圆轴扭转切应力-变形量理论公式的适用对象相同，即满足：均匀性、连续性、各向同性、线性小变形等诸多条件.

1 薄壁圆管

1.1 扭转切应力薄壁圆管扭转切应力分析在材料力学、工程力学等教材中一般都有讲解［5-9］，为保持本文整体上的独立可读性与完整性，并方便论文后半部分对其引用，现做简要介绍.

圆管外圆半径与内圆半径的平均值称为平均半径，用R0表示；圆管厚度即外圆半径与内圆半径的差值用δ表示，通常把δ/R0≤1/10的圆管称为薄壁圆管，否则为厚壁圆管.设某薄壁圆管两端受到扭矩T的作用，受扭前后分别如图1所示.在图1b中沿垂直轴线的1-1截面假想截断后取左边半圆管为研究对象，并让左边仍然保持截断前的静力学平衡状态.设左边环形断茬面上受到均匀切应力τ的作用，如图1c所示，由于壁很薄，可以近似认为切应力沿壁厚均匀分布.

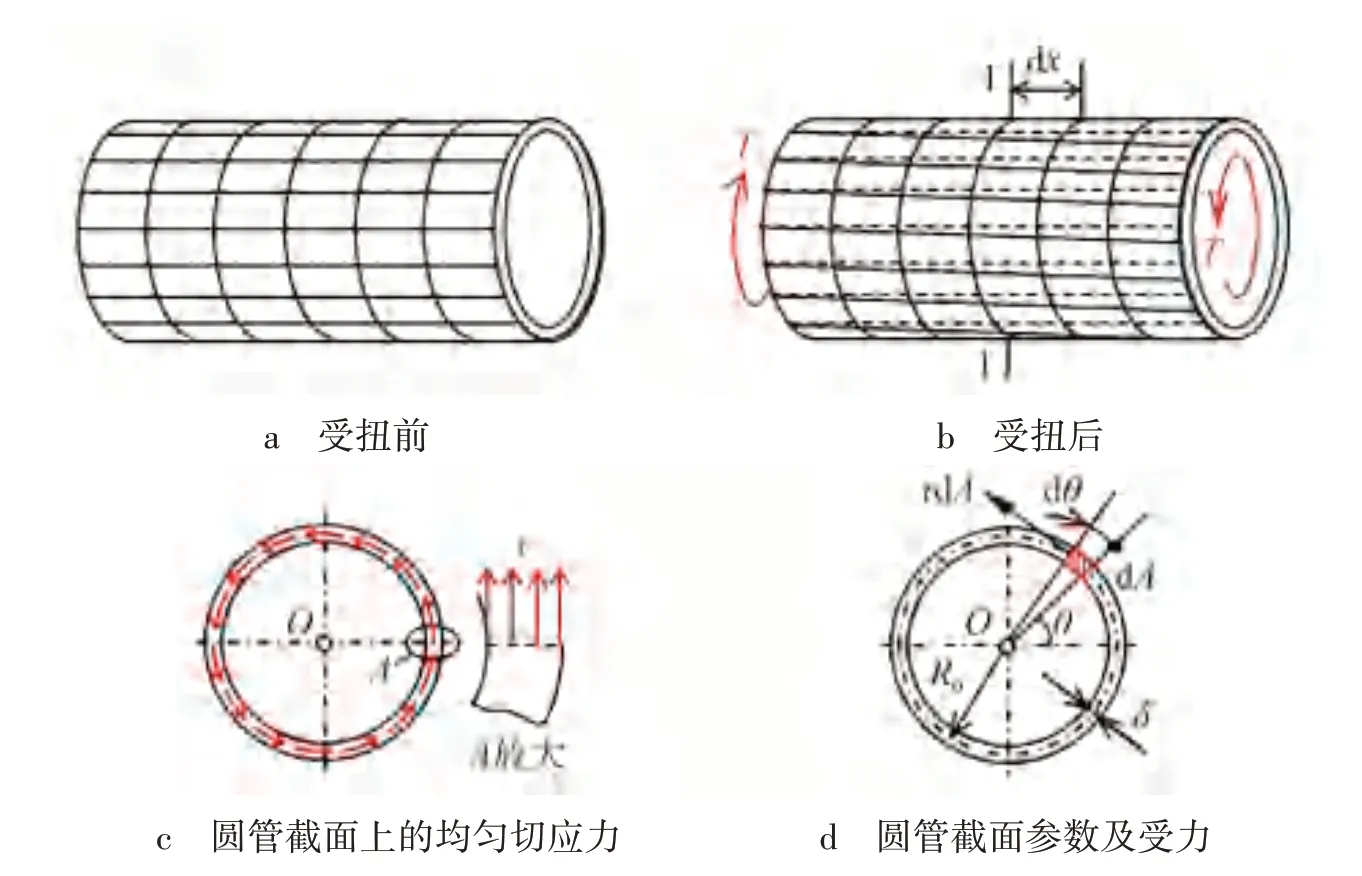
图1 薄壁圆管受扭前后对比及横截面上切应力分布

图1中T表示圆管两端面上受到的扭矩；R0表示圆管平均半径；δ表示圆管厚度.

在图1c中，环形切应力流形成的力系向截面圆心O点简化，力系主矢为零（对称），主矩等于外扭矩T.如图1d所示，

这就是薄壁圆管受扭时横截面上切应力计算公式.

1.2 扭转变形在图1b中，沿1-1截面右侧截取长度为dx的一段圆环，放大后如图2a所示.设受扭后圆环右端面相对于左端面转过的角度为dφ，微体abcd距离观察者最近，设该微体上边缘转过的角度为γ，如图2b所示（已再次放大）.微体abcd受扭后为abc＇d＇.根据观察知道γ角（即切应变）很小，于是有

图2 薄壁圆管扭转变形

式（2）带入剪切胡克定律公式即τ=G·γ，则有τ=GR0·，带入式（1）得

式（3）反应了薄壁圆管扭转时的变形情况，等号左边为薄壁圆管单位长度扭转角.

2 厚壁圆管

2.1 扭转变形如图3所示，假设厚壁圆管是多个薄壁圆管的套装组合，其受扭处都存在一个垂直于轴线的刚性圆片，刚性圆片与各薄壁圆管都焊接在一起，外部扭矩作用在刚性圆片上，刚性圆片把外部扭矩分配到各套装薄壁圆管上.各薄壁圆管对应的单位长度扭转角都由式（3）确定，由于各薄壁圆管都焊接在刚性圆片上，所以受扭后其变形步调一致，即单位长度扭转角必然相等，于是由式（3）得

图3 厚壁圆管扭转

其中，T1，T2，T3，…，Tn分别表示第1，2，3，…，n个薄壁圆管端面上受到的刚性圆片分配的扭矩；R1，R2，R3，…，Rn分别表示第1，2，3，…，n个薄壁圆管的平均半径；dR表示各薄壁圆管的统一厚度.

2.2 扭转切应力厚壁圆管由多个薄壁圆管套装而成，设其中第i个薄壁圆管横截面上的切应力为τi，由式（1）得

式（5）为厚壁圆管扭转时的变形量即单位长度扭转角计算公式；式（7）和（8）同属切应力计算公式，这些公式与教材上基于楔形微体理论推导出的公式相同［5-9］.这种相同性并非偶然，因为2 种推理方法都满足扭转平面假设，即圆轴受扭变形后横截面仍然保持平面，其形状、大小、间距都不改变，而且半径仍然为直线段［5-9］.笔者把厚壁圆管看作由多个薄壁圆管套装在一起，这些薄壁圆管受扭后变形步调一致，即单位长度扭转角相同，所以各薄壁圆管之间没有相对运动，也就没有摩擦力.或者说不计摩擦，把厚壁圆管直接看作由多个光滑的薄壁圆管套装在一起.

另外，扭转平面假设提到圆轴受扭后形状、大小、间距都不变，即直径不变、轴向长度不变，说明直径方向和轴线方向的正应变都为零，由公式σ=E·ε（即正应力等于弹性模量乘以正应变）可知：这2 个方向的正应力都为零.再由公式σ=F/A（即正应力等于拉力或压力除以受力面积）可知，受扭后圆轴在直径方向和轴线方向都不受力，说明将厚壁圆管看作由多个薄壁圆管套装在一起时，各薄壁圆管之间不存在直径方向上的相互压力或拉力，没有压力就没有摩擦力，即各薄壁圆管相互之间没有摩擦力.

3 厚壁圆管切应力-变形量公式对薄壁圆管的适用性分析

薄壁圆管切应力-变形量计算由式（1）和（3）确定；厚壁圆管切应力-变形量计算由式（5）、（7）和（8）确定.实际上式（5）和（8）不但适用于厚壁圆管，也适用于薄壁圆管.

例1 设某薄壁圆管平均半径为R0，壁厚为δ，两端受到扭矩T作用.试分别按薄壁圆管和厚壁圆管计算切应力-变形量，并比较2种算法的差距.

解 令δ/R0=λ即δ=λR0，λ为常数.按厚壁圆管处理时内外直径及IP、WP依次为

其中，ξτ表示2种算法应力差值在厚壁圆管最大切应力中所占百分比.

再由式（3）和（5）得2种算法的单位长度扭转角

由式（9）和（10）可知，λ趋近零时ξτ，ξφ也都趋近零.这说明薄壁圆管管壁越来越薄时，无论用薄壁圆管公式还是用厚壁圆管公式，由此计算出的切应力及单位长度扭转角差距都会越来越小.表1 列出了不同λ值时的ξτ和ξφ值，进一步证实了此观点.

表1 不同λ值时的ξτ、ξφ值

由于假设薄壁圆管扭转切应力沿壁厚均匀分布，所以管壁越薄则薄壁圆管的切应力-变形量公式就越准确.厚壁圆管的切应力-变形量公式是由积分得到的：把圆管划分为无穷多个厚度无限趋近零的薄壁圆管，再依次用薄壁圆管公式计算切应力-变形量，然后叠加.因此有理由认为，厚壁圆管切应力-变形量公式也适用于薄壁圆管，而且计算精度更高.

例2 两圆管套装在一起，内管内外直径依次为d、d1，外管内外直径依次为d1、D.两圆管长度相等、切变模量都为G，两圆管左端面焊接在同一个刚性端盖上、右端面焊接在另一个刚性端盖上，在两端刚性端盖上各加一个旋向相反的扭矩T.求：1）右端盖相对于左端盖绕圆管轴线转过的角度；2）圆管的最大切应力.

解 1）内外圆管右端面相对于左端面绕轴线转过的角度相同，所以两者的单位长度扭转角相同.由式（5）得

其中，T1和T2分别表示内、外圆管受到的扭矩，IP1和IP2分别表示内、外圆管的极惯性矩

从例2计算结果即式（12）和（13）可知，2个圆管套装后的单位长度扭转角和最大切应力，等同于套装后整体上作为一个圆管的单位长度扭转角和最大切应力.同理，多个圆管套装后整体上等同于一个圆管，或者说一个厚壁圆管可以分解为多个（甚至无穷多个）薄壁圆管的套装组合.例2 间接验证了“基于多个薄壁圆管套装假设的圆轴扭转切应力-变形量分析”理论及公式的正确性.

4 用薄壁圆管扭转实验检验剪切胡克定律的正确性

设某薄壁圆管两端受到扭矩T作用，如图4a 所示，受扭前圆管表面平行于轴线的母线如图中虚线所示，受扭后母线如图中实线所示，变为螺旋线.薄壁圆管切应变即γ角如图4a所示，大小由式（2）确定.由式（2）可知，切应变γ角实际上就是母线在薄壁圆管受扭后所形成螺旋线的螺旋角正切值，由于其很小，故γ角近似等于其正切值.如图4b所示，在直角三角形ABC中，AB边代表薄壁圆管的轴向长度L，令BC=R0·φ，φ角表示受扭后薄壁圆管右端面相对于左端面绕轴线转过的角度，结合式（2），则有

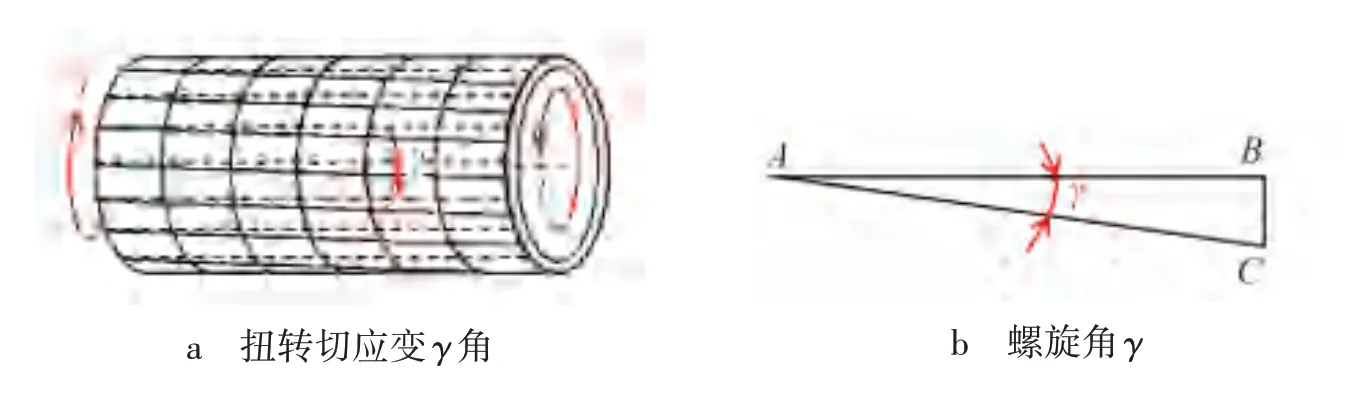
图4 薄壁圆管扭转后的切应变γ角

当φ=2π 时，L就等于螺旋线的螺距H，即γ≈tanγ=可以想象，螺距H相对于平均半径R0而言是很大的.

当前教材一般都没有给出切应变参数的测量方法，也没有给出切应变与切应力之间符合正比例关系即剪切胡克定律公式的正确性验证方法，而是直接理所当然地给出剪切胡克定律公式并加以引用［5-9］.由于缺乏必要的验证性实验，而让切应变这一物理参数显得很抽象，甚至有初学者怀疑该参数的实际可测性.从式（14）即切应变γ角的表达式可以看出，该参数看得见、摸得着，是可以实际测量的.

若把图4b所示直角三角形ABC纸片粘贴在图4a所示薄壁圆管的圆柱面上，让直角边AB与受扭前圆柱母线重合，则贴合后斜边AC就与薄壁圆管受扭后母线形成的螺旋线重合.

材料力学课程实验一般有2 个：拉伸和扭转.建议把扭转试验中的实心圆轴改为薄壁圆管或另外增加薄壁圆管扭转实验.在可行性方面，文献［11］报道了用百分表测量铝制薄壁圆管剪切模量G的方法；文献［12］提到对圆管两端加柱塞，以辅助装夹圆管.式（1）为薄壁圆管受扭后横截面上切应力τ的计算公式；式（14）为薄壁圆管受扭后切应变γ角的计算公式.由剪切胡克定律可知τ与γ成正比，比例系数即为材料的切变模量G.因此，可以用薄壁圆管扭转实验测量切应变γ角和切应力τ各自的具体值、可以检验剪切胡克定律的正确性、可以测量材料的切变模量G.如果再结合材料力学中拉伸实验所测的弹性模量E、泊松比μ的值［13］，还可以检验参数G、E、μ三者之间的关系，即式（15）的正确性.

5 用薄壁圆管辅助证明切应力互等定理

设某薄壁圆管两端受到扭矩T作用，如图1b 所示，沿1-1 截面假想截取长度为dx的圆环微段，放大后如图2a 所示.再假想割取距观察者最近的微体abcd，该微体割取前后受力平衡，如图5所示（微体已放大）.微体左、右两侧面受到的切应力τ大小由式（1）确定、方向则相反，切应力乘以侧面面积得切力，于是左、右两侧面的切力大小相等、方向相反，形成顺时针力偶.为使微体受力平衡，顶面和底面必有反向切力形成逆时针力偶，设顶面和底面的切应力为τ1，则有

图5 切应力互等定理

即

其中，dx，dy，δ分别表示微体的长度、宽度和厚度；dv表示微体体积，dv=dx·dy·δ.

式（16）即为切应力互等定理表达式，即在微体互垂截面上，垂直于截面交线的切应力大小相等，方向都指向或背离交线.图5中微体左、右两侧面上的切应力τ由式（1）确定；顶面和底面上的切应力τ1是通过静力学平衡理论求解得到.如果τ1不存在即τ1=0，则微体将不再受力平衡而必将加速运动，这与客观现实不相符，因此τ1必然存在.对微体列静力学平衡方程，求解得τ1=τ，从而得出切应力互等定理.整个逻辑推理过程理顺成章，很有说服力，易于被初学者接受.有些教材在完全忽略图1b、图2a情况下直接在绪论中利用图5所示微体证明切应力互等定理［7-8］，此做法可能不便于学生自主学习.

6 小 结

1）以薄壁圆管的切应力-变形量理论公式为基础，把厚壁圆管和实心圆轴看作是由多个薄壁圆管套装在一起，由此导出了厚壁圆管和实心圆轴的切应力-变形量公式，结果与教材中基于楔形微体理论导出的公式相同.

2）厚壁圆管的切应力-变形量公式也适用于薄壁圆管，而且计算精度更高.

3）对于当前材料力学课程中的扭转实验，建议用薄壁圆管替代实心圆轴，或另外增加薄壁圆管扭转实验.这样可以验证剪切胡克定律的正确性，可以测量切应力、切应变及材料切变模量G.切应变γ角是薄壁圆管母线在圆管受扭后所形成螺旋线的螺旋角.

4）建议用受扭薄壁圆管辅助证明切应力互等定理，否则会让证明过程中涉及到的微体成为无本之木、无源之水，初学者甚至会怀疑这种微体在工程实际中的客观存在性.