主成分分析的改进及其在疫情后住宿餐饮业中的应用

何秀丽，米 鹏

（河海大学 理学院，江苏 南京 210098）

统计学是机器学习和大数据发展的基础.主成分分析，是统计学中一种重要的综合评价方法［1］.利用统计软件解释大数据的基本思想是一项新的研究热点，借助计算机模拟技术，解决了统计学中的一个常见问题.通过经济实例演示，加深了学生对大数据处理思想和方法的理解.

主成分分析是一种提取重要信息和主要信息同时防止信息损失的方法，以此达到降维的目的.目前，主要被应用在经济、教育和人口等方面，一些欧美统计学家将其应用在人脸识别和医学等领域，并取得了较好的结果.主成分的提取是此方法的核心，目前常用非线性方法和恰当的核函数来提取主成分.一组变量，如果存在相关关系，就可以采用主成分法来处理.主成分法就是通过正交旋转将这些变量变为数量更少的变量，对这些变量的信息进行浓缩.在实际问题中，可以化繁为简，将多指标问题尽可能压缩、降维，使得各维度之间线性无关，其中方差较小的那些维度上的数据被剔除，因此能够简单直接地处理问题.具体来说，选择n个看起来都很重要的指标，对其分析过程有可能过于繁琐.此时，需要利用主成分法进行信息浓缩.指标间常见的关系是线性关系，通过主成分分析后，得到的指标数可能远小于n.降维后的主成分指标覆盖了最初的指标信息，简化了分析变量（即从n维降到远小于n维），同时也不丢失精度［2］.近些年来，主成分分析法也在多方面得到了应用.钱赟［3］通过主成分预测了股票初始价格和收盘价格；吴明娟［4］将主成分应用于癌症基因图谱中的测序；侯娟［5］将主成分应用于山西省的土地绩效评价，并对该省的土地利用提出了合理建议.

一个国家的餐饮和住宿受到文化、地域、居民生活水平、消费水平和消费习惯等诸多因素的影响，最近三年又受到疫情的影响，而这些因素之间又相互影响，比如，因为疫情，人们的工资水平和消费水平会显著降低.从样本数据出发，介绍主成分思想和改进后的方法步骤，并将此方法应用于近两年国内的餐饮和住宿，介绍疫情对此行业的影响.

1 主成分思想及改进方法

其几何意义是，ti是第i主成分的方向，而yi是x在该方向的投影，其方差D(λi)反映了在该方向的分散程度.

步骤3找出R的特征值和特征向量.计算出所有p个结果后（理论上有p个特征值），将其由大到小排序λ1≥λ2≥…≥λp≥0，然后单位化得ei(i=1，2，…，p).

步骤4针对主成分找出贡献率及累计贡献率，分别为

算出累计贡献率达到85%～95%的特征值λ1，λ2，…，λm，对应的主成分为第1，2，…，m(m＜p)主成分.

步骤5计算主成分的荷载.通过如下式子即可求出

以上即为所有主成分的计算步骤.需要注意的是，提取主成分时，要确保累计贡献率达到一定值，这是此方法是否可行的判断标准，要求降维后的信息依然能够使用，并保持一定水平，这样其实际意义也有合理的解释.如果得到的只有空谈的数字而没有实际意义，那么结果也没有任何说服力.

2 改进后的方法的实现和应用

2020年初，新冠疫情席卷全球，受影响最大的是实体经济.利用主成分方法，观察疫情暴发以来中国的住宿餐饮业出现的变化.使用的综合评价以及基于主成分分析的研究方法，部分参考张鹏［8］、解素文［9］、洪素珍［10］等文献.根据2020年中国统计年鉴，选择按注册类型和行业分限额以上住宿企业和餐饮企业主要指标（以下简称住宿业指标和餐饮业指标）2 类数据，取自中国统计年鉴第十七章住宿第二、四节数据.由以上四组、两类数据，利用统计软件，使用主成分分析法，分析2020 疫情发生后各项主要指标对各类型的住宿和餐饮在经济上的影响变化［11］，并通过主成分法对这些重要指标进行降维，讨论了几项主要指标的重要程度，并分析了各类型企业在经历疫情后的综合经济状况及变化.

最初有14维32个样本，可以看出此数据量的差异非常大.选择了4组数据，这里以2020和2021年的住宿业指标为例，这14维的指标分别为：法人企业（个）、从业人数（人）、营业额、客房收入、餐费收入、资产总计、流动资产合计、固定资产净额、负债合计、所有者权益合计、营业收入、营业成本、税金（后12个变量单位为亿元）及附加以及利润总额（亿元），分别用x1，x2，…，x14表示.而32个类型的企业分别为内资企业、国有企业、集体企业、股份合作企业、一般旅馆、民宿服务、露营地及其他住宿业等.餐饮业与住宿业的指标大同小异，接下来进行主成分分析.

取2020 年住宿业的输出结果为例作解释，其他数据将展示但不做解释.表1 展示了所有变量间的相关性，即相关矩阵.这也对应了之前在提取栏选择的“相关性分析”.利用此选项可以知道变量之间相关性，如果数值过低那么不利于主成分分析，不能较好地降维，即使得出了主成分，也不能较好地解释其主成分意义.因此，一般情况下，当原始数据之间的相关性大部分能够大于0.3 则有较好的结果.如表1 所示，大部分变量的相关达到了0.9 以上，说明有较强的相关性，主成分分析能有理想的结果.由于原始数据单位不统一，个、人、亿万元等单位，所以选择“相关性分析”，此方式能够标准化数据.这样得到的数据更有说服力，避免不同的数量级数据出现在同一模型中.

表1 相关矩阵

表2展示了公因子方差.反映变量对于原数据的解释能力，值越大则解释能力越强，其功能类似于特征值，数值越大，其在主成分中所占比重越大.一般情况下，值大于0.5则说明可以解释原始数据.如表1所示，该问题下各个变量的公因子方差都接近于1，大部分都大于0.9，说明每个变量的解释能力都很强，可以较好地代表原始数据.

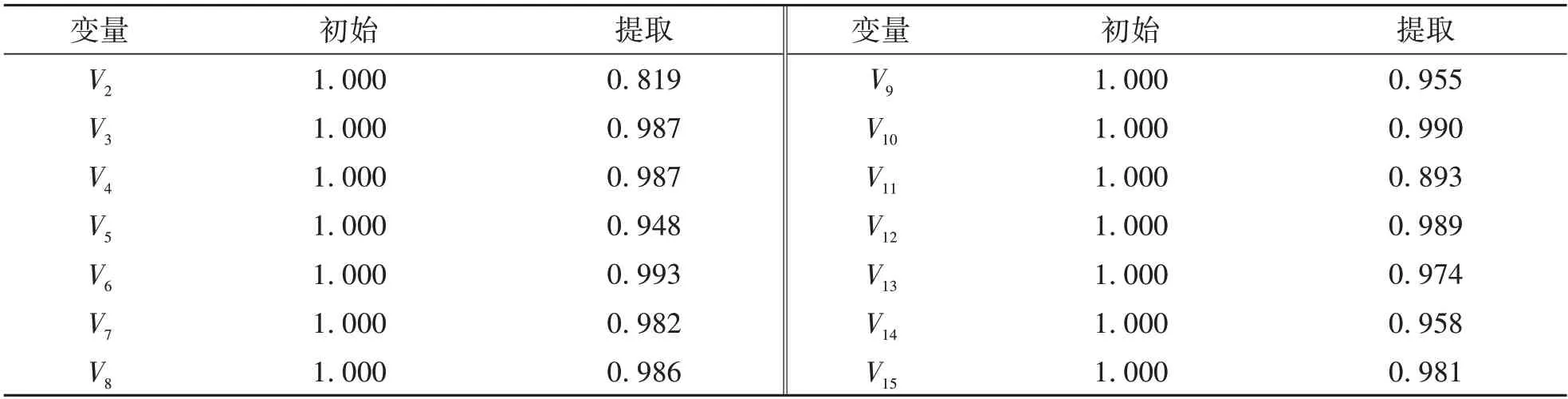
表2 公因子方差

表3 为KMO 和巴特利特球形度检验，此项指标刻画变量之间的关联程度，其中KMO值若大于等于0.60 或者显著性水平值小于等于0.05 则说明变量之间的关联程度较大，由其作主成分也能得到较好的结果.表3所示的KMO值为0.796而且显著性水平也非常小，达到了预期要求，说明该问题有较好的相关性，能够得到有价值的结果.

表3 KMO和巴特利特球形度检验

表4为总方差解释.该表展示了主成分、对应特征值、累计贡献率.可看出，特征值大于1的主成分以及主成分累计贡献率达到预期要求的80%的数量.表4 仅显示一个主成分，其贡献率就达到了96.02%，非常高.一个指标就可以代表14 维的原始数据，效果也非常好，也侧面说明了该问题的主成分分析很有价值.

表4 总方差解释

图1 为“碎石图”，为表4 中14 个主成分对应的特征值，可以看到仅仅第一主成分的特征值比例比较大，已经可以代表所有原始变量.

图1 碎石图

表5为成分矩阵，展示了从大到小排序的所有变量.通过成分数据计算主成分表达式，然后将样本值代入计算即可.2个主成分可分别解释为营业成本大类和营业额大类，对其造成影响的各因素都可计入其中.这份数据可以对此行业的经济状况作出评估.

表5 成分矩阵

由于2020 年住宿业的数据仅得出一个主成分，则不能生成载荷图，即成分图.但通过2020 年餐饮业数据得到了2 个主成分，如图2 所示，该图展示了14 个变量可以被分为2 个大类，即2 个主成分.2 个主成分越聚在一起，则说明越相关.可以看到，大部分的住宿企业，受到疫情暴发的影响较大.人们外出减少，娱乐减少，多数人居家办公，减少了旅游、出差，自然也就减少了住宿业的收入，其综合评价也随之降低.例如旅游饭店类型的企业，综合评价指标降低了0.2，股份有限责任公司降低了0.1，其中影院就属于股份有限责任公司.这些企业，受疫情影响停工停产，客户减少，业务减少，资金流转不过来，直至破产.旅游饭店之类的企业，在疫情期间甚至没有生意，为了生存只有关门，或者拓展业务.当然，仍有部分类型的企业不减反增，例如国有企业增加了0.02，主要是国家的防疫政策对国有企业的补偿措施到位，所以没有遭受过大的经济波动.

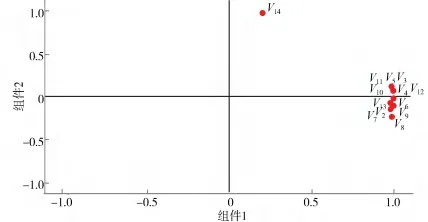
图2 2个主成分（2020餐饮）

餐饮业的变化与住宿业类似.受到疫情暴发的影响，餐饮业运营成本显著提高，餐饮消费更为保守，外出就餐人数和次数减少.为了生存，商家不得不拓展业务，选择转型加入外卖服务，比如入驻外卖平台，加入线上销售等方式，外卖所占比额逐渐增加.疫情后的餐饮和住宿被动重新洗牌，一方面餐饮和住宿公司要加强服务场所防控管理，另一方面政府需要重塑消费者信心，帮企业渡过难关，提高其抗风险的能力.