高空大型无人机下投探空观测资料分析
高 涛,郭 然,刘振宇,孙 夏,王博坤
(1.海南省气象探测中心,海南 海口 570203;2.中国气象局气象探测中心,北京 100000;3.海南省南海气象防灾减灾重点实验室,海南 海口 570203)
台风是全球发生频率最高、影响最严重的自然灾害之一,我国东南沿海地区饱受台风袭扰,造成了社会、经济上的严重损失[1-2].卫星、雷达等传统的台风遥感观测技术,缺乏对台风内部结构及其演变的深入认识,是限制台风强度及台风路径预报准确性的主要因素[3-4].为此,国内外开始探索使用飞机对台风进行抵近观测,通过下投探空获取高分辨率的三维温度、湿度、风向、风速、气压等观测资料.美国最早在1943年进行了有人飞机穿越台风飞行观测[5],20 世纪 90 年代开始进行机载下投探空台风观测试验,2010年启用了目前全球最先进的高空大型无人机“全球鹰(Global Hawk)”,至2018 年“全球鹰”已开展47 次观测,投放约2 700 枚下投探空仪[6],获取台风内部的温湿压风等观测数据,并在数值模式中应用,明显提高了数值预报的精度,美国目前已建立了较为完善的大型无人机气象探测业务[7];中国台湾2003—2012 年实施了为期10 年的代号为“追风计划”的“侵台台风之飞机侦察及下投探空观测试验(Dropwindsonde Observation for Typhoon Surveillancenear the Taiwan Region,DOTSTAR)”,针对西北太平洋49个台风完成了64航次有人飞行观测任务,投放1 051 个下投探空仪[8],获取资料同化到数值模式后对台风路径预报能力有较显著提升[9];中国大陆在2008年首次使用小型无人机飞抵距离台风中心约100 km处进行观测并成功回收无人机,验证了小型无人机具有探测台风边界层气象要素的能力[10-11],2009 年首次进行了有人飞机探测台风试验,在台风“莫拉克”和“天鹅”之间云系相对薄弱的地方飞行并下投探空仪,同化下投探空资料后,0~48 h台风路径预报误差比原来减少18%[12].
2020 年6—8 月份,中国气象局在海南组织实施海燕计划首次试验,成功使用高空大型无人机翼龙-10 对2003 号台风"森拉克"进行抵近观测,正式翻开了我国使用高空大型无人机进行气象观测的篇章.此次试验使用的无人机飞行高度大于10 km,飞行速度500 km·h-1,探测航程大于2 000 km,具备高空、高速、长航时气象探测能力,搭载了下投探空系统和毫米波测云雷达,相对于小型无人机在探测高度、探测范围和探测能力上具有明显优势.
下投探空仪在高空、高速环境下投放在我国尚属首次,其探测性能有待验证.国内海上高分辨率垂直探空资料非常匮乏,与再分析资料的差异性分析结果有助于海上再分析资料的订正.本文使用2020 年8月2 日利用高空大型无人机对2003 号台风“森拉克”抵近观测获得的下投探空资料与常规探空资料以及再分析资料进行对比,以了解高空、高速条件下下投探空资料的可用性及其与海上再分析资料的差异性,并讨论可能影响下投探空观测准确度的因素,为改进高空大型无人机下投探空观测提供参考.
1 资料与方法
1.1 下投探空资料下投探空资料来自“海燕计划”2020 年8 月2 日在海南进行的首次高空大型无人机观测试验,由于此次使用的无人机尚不具备稳定的“绕台”“穿台”能力,因此选择在距离台风中心约400 km 的外围云系进行探测.探空仪投放高度约10 000 m,从投放到落海的时间大约为15 min.探空仪具有较高的垂直分辨率,每1秒记录一次环境温度、相对湿度、气压,位势高度使用气压、温度和相对湿度计算得到,风向、风速以及经纬度、高度使用北斗和GPS 双模卫星导航定位信息计算得到.温度、相对湿度、气压基测最大允许误差分别为±0.3 ℃、±5 %和±1.5 hPa,定位最大允许误差水平方向为8 m,垂直方向为15 m.使用资料前,参考业务探空观测数据质控方法对数据进行了质量控制.此次试验持续3 小时58 分,获得有效探空数据27 组,总样本量13 805 条,图1 为全部下投探空观测数据各要素廓线图.
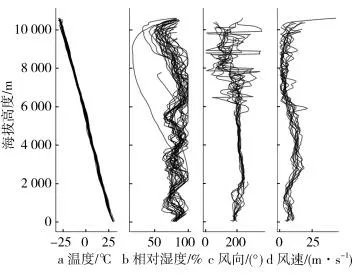
图1 下投探空数据廓线图
1.2 常规探空资料常规探空资料为试验当天邻近探空站(三亚站)秒级数据,观测要素包括温度、相对湿度、风向、风速、气压、位势高度.三亚站距离下投探空仪投放点最近约41 km,最远约256 km,三亚站观测时间为20:00,下投探空观测时间为15:35 至18:20.由于常规探空和下投探空存在时空差异,下垫面、云层分布等不一致,可能对对比结果产生影响,因此两种资料的对比分析结果仅作为下投探空资料可用性评估的参考.
1.3 再分析资料再分析资料为欧洲中期天气预报中心(ECWMF)的ERA5 资料,在时间和空间上与下投探空资料匹配,为了尽可能多地反映两种资料的细节差异,选用了ERA5在300 hPa 至1 000 hPa区间全部20 个标准气压层(300、350、400、450、500、550、600、650、700、750、775、800、825、850、875、900、925、950、975、1 000 hPa)的位势高度、温度、湿度、东西风速、南北风速(东西风速和南北风速换算成风向、风速)数据,水平分辨率为0.25°×0.25°,时间分辨率为1 h.
1.4 分析方法下投探空和常规探空资料按照100 m 的垂直分辨率进行线性插值,得到高度对应的数据序列;下投探空与ERA5 资料在时间和空间上进行对应:时间上,使用与下投探空同一小时的ERA5 资料;空间上,垂直方向使用线性插值方法得到下投探空在20个标准气压层的数据,使用三值滤波减小跳变值影响,水平方向使用反向距离权重法将ERA5资料插值到对应的探空仪位置上,从而得到三维空间上位置匹配的数据序列.
对比分析下投探空和常规探空以及下投探空和ERA5的一致性,指标选用误差(Bias)、平均绝对误差(MAE)、均方根误差(RMSE)、标准差(σ)比值、相关系数(R).误差为两者的差值,反映两者大小关系及误差大小;平均绝对误差是两者绝对误差的平均值,可以避免误差相互抵消的问题,能准确反映两者误差的大小,值越小说明两者误差越小;均方根误差为误差的平方与观测次数比值的平方根,对异常值反应敏感,值越小说明两者误差越小;标准差比值为标准差的比值,和相关系数一起反映了两者变化趋势的相似性,值越接近1 表示两者相似程度越高.计算相关系数时,由于风向角度的周期性,当两者风向差值的绝对值大于180°时,较小风向需向加360°[13].
式(1)-(5)中x、y表示参与计算的两组数据,xi(yi)表示第i次观测数据.
泰勒图能够直观反映两组数据之间的一致性程度.基于余弦定理,泰勒图将标准差、相关系数和均方根误差三种统计数据显示在一张图中.以其中一组数据为观测场,另一组数据为模拟场.从原点到各点的径向距离与标准差成正比,方位角给出两者的相关系数,距离观测点的距离表示两者的均方根误差.本文中,由于温度、湿度、风向、风速度量单位不同,为了比较两者不同要素间的一致性水平,需要对标准差和均方根误差进行无量纲化处理.无量纲标准差()为模拟场标准差与观测场标准差的比值,无量纲均方根误差(RMSE')为中心化均方根误差,需要注意的是,观测场的标准差是由其自身归一化的,因此总是绘制在距离原点一个单位的位置上[14].
无量纲标准差定义为:
无量纲均方根误差定义为:
式(6)、(7)中x表示观测场,y表示模拟场,xi(yi)表示第i次观测数据.
此外,在对比下投探空和EAR5 的湿度数据时,由于冰过饱和原因,需要将0 ℃以下的下投探空湿度数据转化为相对于冰相的湿度,转化公式为:
式中RHice表示冰相相对湿度,RH表示空气相对湿度,ew表示水面饱和水气压,ei表示冰面饱和水气压.ew和ei计算公式如下:
式中T为绝对零度,t为温度.
2 结果分析
2.1 下投探空与常规探空对比分析图2 为下投探空和常规探空各要素的泰勒图,常规探空数据为观测场,下投探空数据为模拟场.可见:下投探空温度分布集中,相关系数均在0.99 以上,标准差比值接近1,距观测点很近,两者呈现强相关性且误差小;湿度分布相对离散,相关系数主要集中在0~0.5之间,标准差比值较接近1,距离观测点较远,两者呈现弱相关性,误差明显大于温度;风向分布离散,相关系数主要介于0.6~0.9 之间,标准差比值接近1,距离观测点较近,两者呈现较强相关性,误差较小;风速分布更加离散,相关系数主要介于0.8~0.95之间,标准差比值整体接近1.5,距离观测点较近,两者相关性较强,误差水平与风向相当.
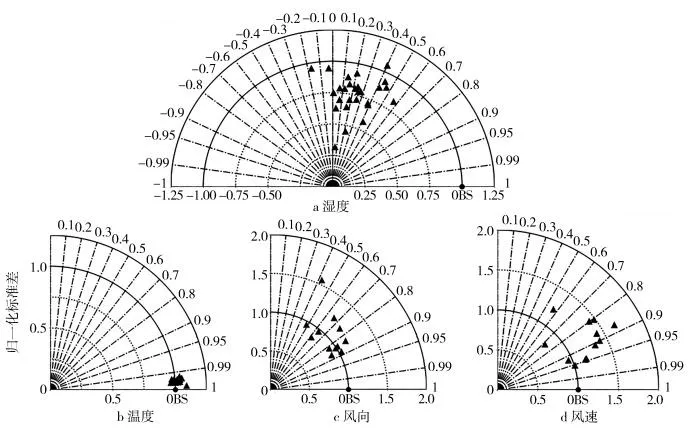
图2 下投探空和常规探空的泰勒图
图3 为下投探空和常规探空平均绝对误差廓线图,能更精确反映出两者误差大小情况.温度平均绝对误差小于2 ℃,湿度大部分小于10%,对流层中上层部分区间在10%~20%之间,风向大部分小于20°,近地面和对流层上层在20°~60°之间,对流层上层误差明显增大,风速整体上小于2 m·s-1,对流层中层部分区域在2~6 m·s-1之间.
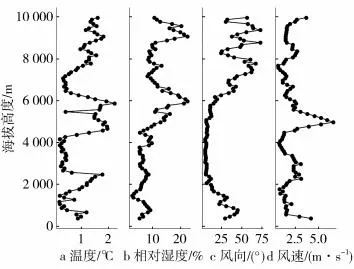
图3 下投探空和常规探空平均绝对误差廓线图
综合泰勒图(图2)和廓线图(图3)来看,各组下投探空之间温度、湿度分布更集中,一致性更好,风向、风速相对较差,风向有明显的离群值;下投探空和常规探空温度变化趋势相似度最高,风向、风速次之,湿度最低,温度、湿度、风速误差水平接近WMO《气象仪器和观测方法的指南》(WMO guide to meteorological instruments and methods of observation,WMO-No.8,the CIMO Guide)[15]的精度要求(温度0.4~1 ℃,湿度6%~15%,风速1~2 m·s-1),风向误差水平在1 700~6 000 m 的高度区间接近the CIMO Guide 的精度要求(风向5°~10°),1 700 m 以下主要受下垫面差异的影响,下投探空的下垫面为海洋,常规探空的下垫面为陆地,各要素在低海拔高度误差较大,风向风速表现明显;6 000 m 以上主要受探空仪高速下落造成下投探空测量误差的影响,这点将在2.3 节进行详细讨论.此外,由于时空差异,两个观测区域的云层分布可能不同,云层内外水汽含量差异较大,一定程度上造成湿度上的误差.
2.2 下投探空与ERA5 对比分析图4 为下投探空和ERA5 各要素的泰勒图,下投探空数据为观测场,ERA5数据为模拟场.可见:ERA5温度分布集中,相关系数均在0.99以上,标准差比值接近1,距观测点很近,两者呈现强相关性且误差小;湿度分布相对离散,相关系数主要集中在-0.6~0.4 之间,标准差比值较接近1,距离观测点较远,两者呈现弱相关甚至负相关,误差水平明显大于温度;风向分布离散,相关系数主要介于0.6~0.95之间,标准差比值接近1,距离观测点较近,两者呈现较强相关性,误差较小;风速分布离散度略好于风向,相关系数主要介于0.5~0.95 之间,标准差比值整体接近1,距离观测点较近,两者呈现较强相关性,误差水平与风向相当.
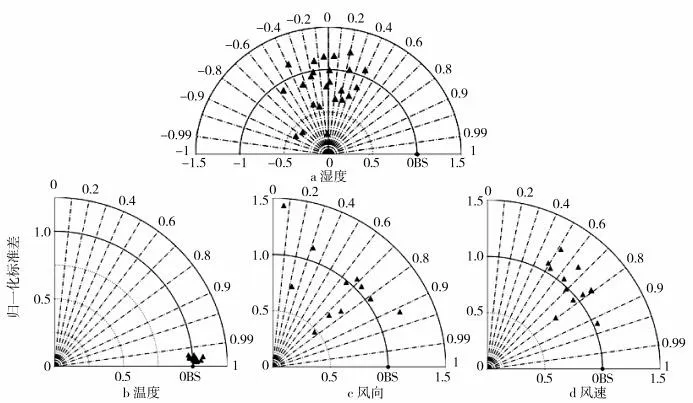
图4 下投探空和ERA5对比的泰勒图
计算各组下投探空和对应ERA5 在20 个标准气压层的误差并取平均,得出平均误差和平均绝对误差,廓线图如图5所示.
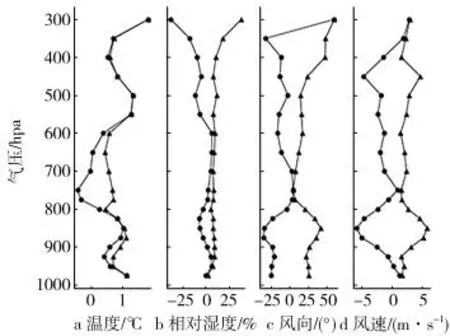
图5 下投探空和ERA5平均误差和平均绝对误差廓线
温度误差介于-0.4~1.8 ℃之间,大部分绝对误差小于1 ℃,在300 hPa达到最大值,随高度没有明显变化特征,基本为正误差,整体上下投探空大于ERA5;湿度误差介于-38%~7%之间,对流层中下层绝对误差小于7%,在300 hPa 达到最大值,对流层下层(1 000~800 hPa)没有明显大小关系,对流层中层(775~600 hPa)下投探空略大,对流层中上层(550~300 hPa)下投探空明显小于ERA5,整体上误差大小随高度增加而增大,对流层上层探空仪测量的湿度大部分偏干20%左右;风向误差介于-35°~60°之间,大部分绝对误差小于25°,对流层中下层和上层误差较大,在300 hPa 达到最大值,基本为负误差,整体上下投探空小于ERA5;风速误差介于在-5.8~2.8 m·s-1之间,除850 hPa外,绝对误差均小于5 m·s-1,对流层中下层误差较大,基本为负误差,整体上下投探空小于ERA5.
综合泰勒图(图4)和廓线图(图5)来看,下投探空和ERA5温度变化趋势相似度最高,误差基本在1 ℃以内,整体上下投探空大于ERA5;风向、风速变化趋势次之,对流层中下层和上层误差较大,风向误差基本在25°以内,风速基本在5 m·s-1以内,整体上风向、风速下投探空小于ERA5;湿度变化趋势相似度最低,除对流层上层外误差基本在7%以内,误差随高度增加而增大,对流层上层下投探空明显小于ERA5.
下投探空和ERA5之间的差异除了受再分析资料本身的估计偏差影响外(海上观测资料相对匮乏,海上再分析资料偏差偏大),还受下投探空仪本身测量准确度影响,包括探空仪降落速度变化、探空仪环境突变以及探空仪测量性能,具体在2.3节讨论.
2.3 下投探空观测准确性影响因素分析
2.3.1 下落速度图6 为全部27 个探空仪下落速度廓线图,每个子图对应1 个探空仪,横轴表示下落速度,纵轴表示对应海拔高度.下落速度在30~40 m·s-1左右时判定为未开伞,下落速度减小至10~20 m·s-1时判定为已开伞,通过对比开伞前后下投探空和ERA5的一致性变化,分析下落速度对下投探空观测数据的影响.
图7 为探空仪开伞前后下投探空和ERA5 不同观测要素的泰勒图(相关系数、标准差、均方根误差取平均值),下投探空为观测场,ERA5 为模拟场.可见:温度分布接近,相关系数均大于0.99,开伞前略大,开伞后标准差比值更接近于1,距离观测点更近,总体上开伞后一致性略好;湿度分布较远,开伞前相关系数约为-0.6,呈现负相关,开伞后相关系数为0.2 左右,相关性明显增强,开伞后的标准差比值更接近于1,距离观测点更近,开伞后一致性明显更好;风向分布相对较远,开伞前相关系数为0.2左右,呈现弱相关性,开伞后相关系数为0.35 左右,相关性有所增强,开伞前标准差比值更接近于1,但开伞后到观测点的距离减小明显,综合来看开伞后一致性更好;风速分布相对较远,开伞前相关系数约为0.3,呈弱相关,开伞后相关性明显增强,相关系数约为0.7,呈强相关,且开伞后标准差比值更接近1,距离观测点明显更近,综合来看开伞后一致性明显更好.
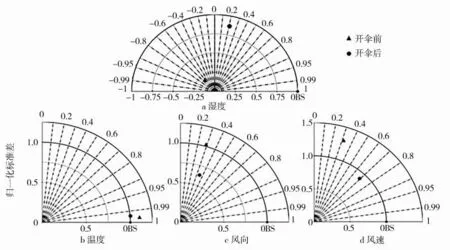
图7 开伞前后下投探空和ERA5各观测要素泰勒图
进一步分析(由于温度开伞前后变化不大,而湿度还受其他因素影响,此处仅进一步分析风向、风速),结合下落速度廓线(图6)和误差廓线(图5)来看,1~12组下投探空(含风向风速数据)大部分在6 000 m 左右开伞,相应的风向误差在6 000 m 以上显著增大,风速没有明显变化;将风向进行8 方位转化,将风速进行风力等级转化,计算开伞前后的一致率,结果如图8所示,开伞前风向、风速均有多组数据一致率为零,开伞后一致率明显提升,开伞前风向、风速平均一致率均为20%左右,开伞后分别提高到45%和35%左右,可见,探空仪以较小速度平稳下落时测得的风向、风速数据更准确.以同样的方法对比下投探空和常规探空可以得出相同结论.
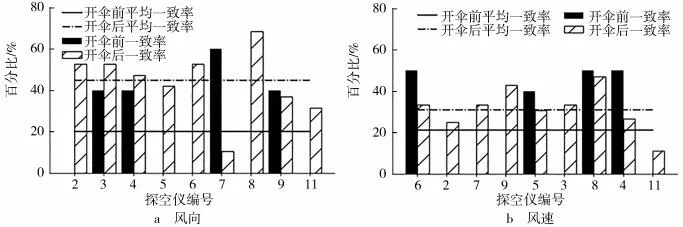
图8 开伞前后下投探空和ERA5风向、风速一致率对比
综上所述,开伞后各要素的一致性均优于开伞前,温度变化不大,湿度、风向、风速变化明显.这种变化与探空仪下落速度有关:湿度传感器响应速度较慢,测量存在滞后误差,高速下落的情况下滞后误差被放大;风向、风速由北斗和GPS 双模卫星导航定位信号获得,高速下落在一定程度上影响了定位精度[16],从而造成风向、风速的测量误差.
2.3.2 传感器测量性能高空(对流层上层和平流层)湿度观测存在较大误差,主要与湿度传感器低温灵敏度差、易冻结有关[17-18],在穿越云层时较为明显.探空仪进入云层时,随着周围水汽含量增加而湿度增加,出云后湿度传感器无法立即脱湿而产生湿滞效应,导致出云后短时间内的测量误差,高空低温云内结冰会加剧误差.此外,此次试验使用的湿度传感器测量范围为0~100%,对于大于100%的湿度无法测量,而对流层上层及平流层由于冰过饱和原因,实际存在湿度大于100%的情况.因此,在湿度传感器测量性能和测量范围的双重影响下,下投探空测量的湿度显著偏小,与唐南军等[19]的研究结果一致.
2.3.3 环境温度突变为了防止存放下投探空仪的吊舱结冰,吊舱配备了加热装置.探空仪投放高度10 000 m左右,环境温度达到-30 ℃,吊舱温度10 ℃左右;探空仪投放瞬间环境温度从10 ℃突变为-30 ℃,瞬间变化近40 ℃,可能在一定程度上影响湿度测量的准确度,具体影响程度有待进一步验证.
3 结论
本文利用2020 年大型高空无人机观测试验的下投探空资料和常规探空资料以及ERA5 再分析资料进行对比,采用误差、平均绝对误差、相关系数、标准差、均方根误差等统计方法,对温度、湿度、风向、风速四种观测要素进行了一致性分析,结果表明:
(1)各组下投探空之间,温度一致性最好,湿度次之,风向、风速相对较差;
(2)下投探空温度、湿度、风速误差水平接近WMO CIMO 的精度要求,在考虑探空仪下落速度和下垫面差异对风向测量影响的情况下,风向的误差水平也接近WMO CIMO的精度要求;
(3)ERA5 温度、中下层湿度与下投探空偏差较小,风向相差较大,风速在1 000~2 000 m 高度区间偏差较大,下投探空上层湿度明显偏干.
(4)下投探空湿度、风向、风速测量准确度受探空仪下落速度影响明显,湿度还可能受传感器测量性能、环境温度突变影响.后续试验可通过缩短开伞时间以降低探空仪高速下落带来的测量误差.
海上高分辨率垂直观测资料的获取对降水分布、台风内部结构及其演变的认识具有重要作用,高空大型无人机的应用无疑在该领域迈出了重要一步.以上结论仅基于一次试验观测数据,样本量较小,部分结论还有待系列观测试验及数据来进行验证.

