秒级探空数据随机误差评估

姚 雯 马 颖

(中国气象科学研究院灾害天气国家重点实验室/雷电物理和防护工程实验室, 北京 100081)



秒级探空数据随机误差评估

姚 雯*马 颖

(中国气象科学研究院灾害天气国家重点实验室/雷电物理和防护工程实验室, 北京 100081)

利用2007年6月和2008年6—7月国内GPS探空仪同步比对试验数据及2010年中国阳江国际探空系统比对试验数据，基于现有的探空仪随机误差的间接计算方法，深入分析不同的探空原始数据平滑处理程度对随机误差评估的影响。分析表明：现有的探空仪随机误差评估方法不能完全适用于秒级探空数据，特别是对风、平流层温度和对流层相对湿度这3个要素的随机误差的评估。在同步比对施放中，如果对探空原始数据的平滑处理程度一致，可以利用现有的随机误差评估方法，不会产生明显偏差；反之，如果平滑处理程度差异较大，则间接计算得出的随机误差会明显偏大。在比对施放方案中，为了更好地获取某种型号探空仪的随机误差，建议将多个同型号探空仪同球施放进行比对观测，避免作为参考仪器的其他型号探空仪自身的误差参与计算，影响待测探空仪随机误差的评估。同型号探空仪同球施放的探空仪越多，获取的有效统计数据越多，随机误差的分析越准确。

随机误差； 同步比对； 平滑处理程度

引 言

探空仪是一种测量地面至高空的大气温度、压力、相对湿度等气象要素的一次性使用仪器。测量仪器均存在测量误差。测量误差一般又分为系统误差和随机误差两种。探空仪要在日晒雨淋恶劣环境下动态测量高层稀薄大气，其测量的困难特别是确定其测量误差的困难比室内静态测量大得多。无论是国际还是国内，一种探空仪型号从研发到进入台站业务使用，除在室内通过静态校准确定各个测量参数的校准线外,还需要通过动态施放反复测定其误差[1-4]。无论是校准线测定还是动态测定，都需要有测量准确度相对较高的标准仪器作为参考,到目前为止，国际上尚未开发出一种令人满意的标准探空仪作为参考，只能通过同步比对施放获得各型号探空仪相互间的相对系统误差和随机误差[5-11]。近20年来，以数值预报初估场为参考，计算高空观测网的各型号探空仪的相对系统误差和随机误差的方法也越来越得到重视[12-13]，但目前世界气象组织(WMO)国际探空系统比对主要还是采用同步比对施放方法获得各国探空仪的性能[14-16]。

随着科学技术的发展和应用，探空仪的数据采集率、准确度以及系统的自动化程度有很大提高。现有的探空系统如我国业务使用的L波段探空系统、GPS探空系统以及正在研发的北斗探空系统，其数据采集率已由原有59-701探空系统的每分钟1组提高到每秒1组，敏感元件的各种误差也有大幅度减小[17-18]，因此，为测定现有探空仪的探测误差进行的比对施放方案、数据处理和计算统计方法也需要不断地改进和完善。从1989年的哈萨克斯坦到2010年的中国阳江国际探空比对， WMO一直利用Kurnosenko开发的评估软件来获取各国探空仪间的相对系统误差，并指定某种型号探空仪为标准，间接计算出其他厂家探空仪的随机误差[19]。该随机误差计算方法假设测量要素在样本足够多的情况下符合正态分布，并根据误差分解原理利用间接计算方法求取。针对分钟量级的探空数据，其随机误差评估结果，各探空仪厂商比较认可，但从2005年毛里求斯国际探空系统比对开始，各国研发的秒级GPS探空系统开始参与国际比对最终报告表明，这种间接计算方法对高空风数据随机误差的估计不尽人意[20]，在2010年中国阳江国际探空系统比对中，参与比对的探空系统均为秒级探空系统，其最终报告对随机误差的间接计算方法也进行了很大程度的改进[21]。因此，针对现有的随机误差间接计算方法能否完全适用于目前秒级探空系统，探空比对的方式和对探空比对数据处理的具体方法是否需要改进等问题，有必要对探空仪测量误差的概念和分析方法，在遵循WMO理念的基础上进行深入的探讨。

1 探空仪测量误差分类

探空仪是测量地面至高空的大气温度、气压、相对湿度和风的一次性使用仪器。即使是同一厂家、同一型号、同一批次的探空仪，由于元器件及生产工艺的细微差异，都会导致其观测数据出现或多或少的差异。仪器误差通常分为系统误差和随机误差两类，系统误差是指在一定的测量条件下，对同一个被测对象进行多次重复测量时，所得结果平均值与被测量的真值之差。由于在实际施放过程中还没有一种探空仪可以作为准确观测0～35 km大气的标准探空仪，大气的真实数据无法知道，因而每种探空仪观测数据偏离大气真值的系统误差目前还无法测定, 只能同步比对施放获取两种型号探空仪之间的相对系统误差。随机误差是指由于偶然或不确定因素(如由于外界环境变化)造成的每一次测量值的无规则变化。具体讲，如果在同一气球下同步比对施放两种探空仪，随观测时间的变化，其测量数据之间可能会存在一些差异。如果大量反复同步施放的是两种不同型号的探空仪，由此获得的探空廓线之间差异的平均值表示的是这两种探空仪之间的相对系统误差。如果同步比对的探空仪属于同一型号甚至还是同一批号，则其获得的探空廓线之间差异的平均值(即相对系统误差)会随着比对施放次数的增加逐步趋于零；但该型号探空仪观测数据的随机误差，由于原材料和生产工艺的些微差异，探空仪个体的具体误差特性等原因会存在不同程度的差异；或者在比对施放过程中由于传感器相对于太阳的取向以及仪器摆动等具体情况不同，也会造成个体之间的差异。虽然单次测量的随机误差没有规律，但多次测量的总体却服从统计规律，通过对测量数据的统计处理，能在一定程度上估计其对测量结果的影响程度。

为了掌握全球或各地区探空站网观测数据的时间和空间一致性程度，通过直接比对施放方法及时获取各种型号探空仪之间的相对系统误差是高空观测工作者的首要任务之一。除相对系统误差外，随机误差也一直是探空界和资料使用者关心的问题，由于用户每天得到的实际观测数据中都包含随机误差，且合理的评估方法获取的随机误差能一定程度反映同一型号探空仪的典型误差特征[20-21]，因此，测定每种探空仪型号观测数据的随机误差，为用户提供必要和可靠的误差信息，以便进一步了解每个高空站观测数据的可靠性也是高空观测工作者的重要职责。

2 探空仪误差的直接比对测定方法

目前在国际或多边探空系统比对中，比较常用的方法是通过多种型号探空仪的同步直接比对施放，并指定其中一种探空仪作为参考仪器，再测定其他型号探空仪与参考仪器之间的相对系统误差。至于随机误差的获取，由于国际比对工作量大，未采用同一型号探空仪自身双施放的方法测定，而是采用在直接比对各种探空仪之间的相对系统误差的同时，用间接计算方法将参考仪器的随机误差作为已知随机误差，再从已知与待测仪器之间的随机误差中分离出未知仪器的随机误差。从1989年哈萨克斯坦的国际探空系统比对到2010年中国阳江的国际探空系统比对中，WMO一直使用Kurnosenko开发的评估软件[19]。虽然软件也在不断完善，但对各参比探空仪在施放过程中的动态随机误差计算方法主要采用间接计算方法。从毛里求斯国际探空系统比对开始，秒级的高精度探空仪开始参加比对试验，其系统的数据采样率已经由以往的分钟级提高到秒级，空间采样率由几十米量级提高到米量级，能够得到探空路径中更多的温、湿、风数据，但也反映出气球摆动引起的变化细节，为了获取更接近于真实大气的情况，各厂家需要对探空原始测值数据进行订正和平滑处理。由于各个厂家的探空软件各自对高精度的探空原始数据进行了复杂程度不同的处理，即使原始测值没有差异，但经过不同厂家软件处理后的最终探空结果将会存在差异。毛里求斯国际比对报告中也明确指出，日本Meisei探空系统测定的GPS原始定位数据与芬兰Vaisala 等系统测得的原始定位数据很接近，而以Vaisala测得的风数据为参考，间接计算获得的Meisei系统的风向风速的随机误差很大，这与Meisei对原始数据的滤波方法有关，Meisei探空系统中风的随机误差偏大是由于其平滑程度与其他系统差异较大引起的[20]。这说明间接计算方法中，对秒级探空原始测值处理的方法造成的两个探空系统探测结果的差异对动态随机误差的计算有影响。2010年中国阳江国际探空系统比对的最终报告中也指出不同型号的探空仪在比对过程中，由于各种因素的变化引起的差异不会均匀分布[21]，因此，在中国阳江国际比对试验中对随机误差的间接计算方法有较大改动，要求用于间接计算采用的参考探空仪应选择对原始数据滤波程度为中等的仪器[20]，表明平滑程度对随机误差的估计密切相关。

3 方法与数据

3.1 探空仪随机误差的计算方法

国际探空系统比对试验中将探空仪比对数据差值的分布按正态分布处理，并假定各探空系统的动态随机误差独立不相关，用两种探空系统(参考和待测探空仪)各高度层观测差值的标准差分布估计待测探空仪的随机误差。待测探空仪的随机误差用间接计算方法获得，即将参考仪器的随机误差作为已知随机误差，再从待测与参考仪器之间的随机误差中分离出待测仪器的随机误差[20-21]。

如任意选取1个探空仪A和1个探空仪B进行同步比对施放，取得1 s间隔的比对观测数据。待测探空仪的随机误差分布情况按照一定的高度层间隔分别进行标准差统计来获得，用以表示该高度层上的秒级探空数据差异偏离差异平均值的离散程度(注下文图中均用各高度层观测差值的标准差来表征随机误差的分布情况)。本文标准差计算参照中国阳江国际探空系统比对的最终报告[21]按2 km高度间隔进行平均处理，由于高精度探空仪获取的是1 s间隔的比对观测数据，2 km高度间隔根据探空仪的升速，不同的施放过程在各高度层上获得的参与比对数据量会有不同(按照5～6 m/s升速计算，每2 km 高度约有300～400组比对数据参与该高度层的标准差计算)。

3.2 数 据

本文所使用的探空比对数据来源为WMO组织的中国阳江国际探空系统比对试验和中国气象局组织的国内探空仪性能比对试验。2010年7月12日—8月1日WMO在阳江组织第8届国际探空比对试验，来自中国、美国、日本、南非、韩国、德国、瑞士、法国、芬兰9个国家的GPS探空仪参加比对，共放球72次，获取各厂家秒级GPS探空数据。由于国际比对工作量大，没有采用同一型号探空仪同步施放的方法直接计算该型号探空仪的随机误差，而是以某一型号探空仪为参考，利用间接计算方法获取其他型号探空仪的随机误差。中国阳江国际探空系统比对最终报告发现尽管参比的高精度探空仪的相对系统误差相近，但利用间接计算方法获取的随机误差存在差异(图1a)。中国气象局2007年6月和2008年6—7月在北京、锡林浩特和阳江组织了3批次国产GPS探空仪与芬兰Vaisala RS92型探空仪同步比对试验，获取各厂家最原始的秒级探空数据。采用中国阳江国际探空系统比对报告中使用的随机误差计算方法对北京站17次参与同步比对试验的Vaisala RS92型探空仪的探空原始测值进行不同的数据平滑处理,分别用直接以及间接的方法对Vaisala RS92型探空仪的随机误差进行计算，分析发现，不同的数据处理方法对其随机误差的计算结果会有影响(图1b)。因此，本文利用中国气象局组织的中国阳江探空系统比对试验中选取2组比对试验的原始数据，其中1组数据为同型号的国产GPS高精度探空比对数据，另1组数据为Vaisala RS92型探空系统提供的原始数据举例分析，从不同侧面探讨秒级探空数据随机误差计算方法。

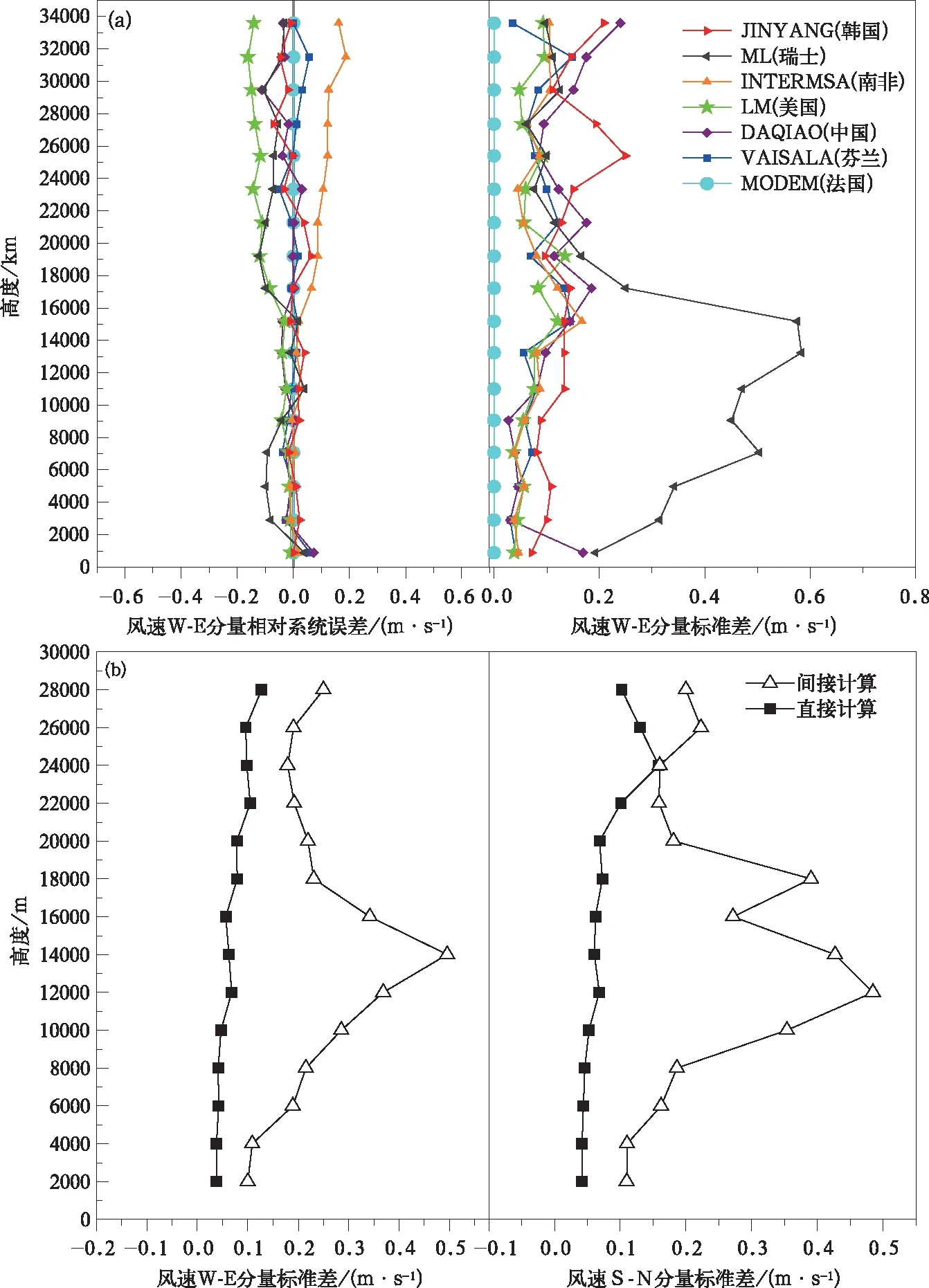
图1 不同厂家探空仪获取的风速相对系统误差及标准差(a)中国阳江国际探空系统比对试验不同国家探空仪风速相对系统误差及标准差(以法国MODEM为参考探空仪)，(b)国内探空比对试验北京站Vaisala RS92型探空仪直接和间接计算的风速标准差Fig.1 Standard deviation statistics of different types of radiosondes(a)systematic bias and standard deviations of wind speed differences relative to MODEM in 8th WMO Radiosonde Comparison at Yangjiang China，(b)standard deviation of upper-air wind speed of Vaisala RS92 GPS radiosondes in radiosonde comparison in Beijing China

4 探空仪风数据随机误差分析

本文对2008年7月17日中国阳江国际探空系统比对试验中3个国产GPS探空仪的一次同步比对施放取得的原始秒级探空数据，分别采用不同程度的平滑处理进一步说明平滑程度对随机误差计算的影响。图 2a 为一次比对施放的高空风W-E和S-N分量廓线。该廓线由3个同型号的国产GPS探空仪(用Ⅰ，Ⅱ，Ⅲ表示)挂在同一气球下同步施放获得。风的分量是从原始的GPS定位数据(1s间隔)经由同一数据处理软件经过30点滑动平均后计算得到。可以看到平滑处理后3条风廓线几乎完全重合(图2a)。

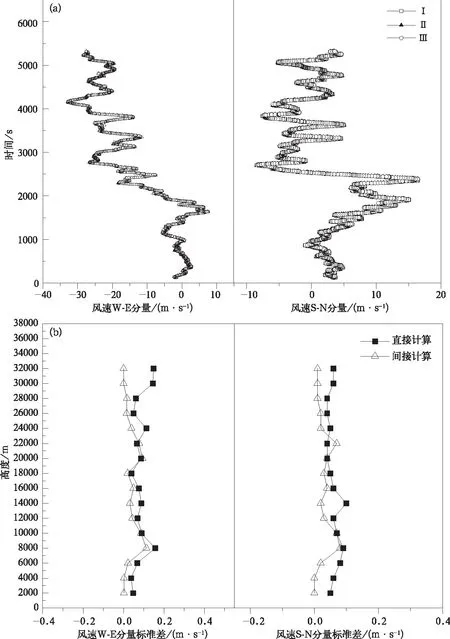
图2 3个同型号国产GPS探空仪经过30点滑动平均处理的高空风速廓线以及各高度层标准差(a)W-E,S-N分量风速廓线随时间分布,(b)按2 km间隔统计的风速标准差Fig.2 Upper-air wind speed profile and standard deviation of three same type of GPS radiosondes by 30 points data smoothing (a)W-E and S-N components of wind profile with time, (b)standard deviation of W-E and S-N components of wind by 2 km interval

参照中国阳江国际探空系统比对方法，对获取的探空比对数据从低到高分层分别进行统计，按2 km 高度间隔分别获取各高度层上的标准差(标准差计算公式略)。图2中风秒级数据均经过30点滑动平均处理。其中,图2b中直接计算表示用探空仪Ⅰ和探空仪Ⅱ的风速差值计算得到标准差，间接计算表示按照国际比对中的间接计算方法，以探空仪Ⅰ的风速标准差为参考，将探空仪Ⅲ与参考探空仪的风速差值的方差减去参考探空仪的方差，间接计算出探空仪Ⅲ的方差，从而得到其标准差。由图2b可知，在探空仪Ⅰ、探空仪Ⅱ和探空仪Ⅲ均经过相同的30点平滑处理下，直接计算与间接计算得到的标准差十分接近(这是1次比对施放数据的结果，如果是多次施放的平均结果，差异更小)，表明在平滑程度一致的情况下间接计算的标准差与直接计算的标准差没有明显差异。

图3采用同一份GPS探空仪原始秒数据资料，但探空仪Ⅰ和探空仪Ⅱ的原始数据采用15点滑动平均，保留了较多因上升过程中气球摆动引起的来回变化细节，而探空仪Ⅲ的原始数据仍采用30点滑动平均。结果探空仪Ⅰ和探空仪Ⅱ直接计算得到的标准差较图2结果略有增大，而间接计算得出的探空仪Ⅲ的标准差增大较多。由图3可见，尽管对探空仪Ⅲ的原始数据平滑程度没有改变，仍然采用30点平滑，但探空仪Ⅰ和探空仪Ⅱ的原始数据采用了15点平滑处理，使用同一计算方法间接计算得出的标准差的差异增大，这说明平滑程度的差异对间接计算风的标准差影响较大。

图3 3个同型号国产GPS探空仪经过15点和30点平滑处理后各高度层风速标准差Fig.3 Standard deviation of upper-air wind speed of three same types of GPS radiosondes by different data smoothing methods

同样，上述3个GPS探空仪原始定位数据，如果对探空仪Ⅰ和探空仪Ⅱ的原始数据平滑程度加大，作120点滑动平均，进一步减少上升过程中气球摆动引起的来回摆动细节，而探空仪Ⅲ的原始数据仍采用最初的30点滑动平均。结果探空仪Ⅰ和探空仪Ⅱ直接计算得到的标准差略有减小，而间接计算得出的探空仪Ⅲ的标准差仍然增大，说明平滑程度的差异对间接计算风的标准差影响大(图略)。

以上对同一原始数据采用不同程度的数据平滑处理结果表明，如果两个探空系统对原始数据的平滑程度一致，可以利用与一个已知标准差的探空仪同步比对的观测数据间接计算另一个探空仪的标准差而不会产生明显偏差。反之，如果两个探空系统对原始数据的平滑程度差异较大，则间接计算得出的标准差明显偏大。

虽然毛里求斯国际探空系统比对数据分析中已发现，具有秒级采样的GPS探空仪能清晰地反映出探空仪上升过程中来回摆动的细节，为了减少这种因气球摆动引起的探测要素波动，需要对原始探空测值进行平滑滤波处理，但当时各国都在试验平滑处理效果，没有统一的方法，对各探空仪的随机误差评估结果不尽人意。2010年中国阳江国际探空系统比对中，对评估方法进行了改进，采用2 km 和250 m 厚度层中的平均风[21]计算探空风数据的标准差，后者间接计算的标准差明显大于前者。再次表明，平滑滤波程度与标准差大小密切相关，数据越平滑，间接计算得到的标准差越小。

5 温度及相对湿度随机误差分析

常规探空记录表明温度廓线在对流层比较平滑，对流层顶以上摆动很大；相对湿度廓线在对流层摆动很大，而在对流层顶以上比较平滑，如果对原始的温度和相对湿度测值进行不同程度的平滑处理，则平滑程度对二者间接计算的标准差也会有影响。为了获得不同平滑程度对温度和相对湿度标准差的影响，将2008年6月4日中国阳江国际探空系统比对试验中3个Vaisala RS92型GPS探空仪(用Ⅰ′，Ⅱ′，Ⅲ′表示)提供的原始数据，按照原始测值、15点滑动平均、30点滑动平均进行不同程度的处理，原始数据的平滑程度越低，温度和相对湿度廓线保留的细节就越多，来回波动越明显；反之，平滑程度越高，3个Vaisala RS92探空仪得到的温度和相对湿度廓线越一致。

图4为3个Vaisala RS92型GPS探空仪在平滑程度一致的情况下计算得到的温度和相对湿度在各高度层的标准差分布。可以看到，未经平滑处理时温度和对流层相对湿度的标准差略微偏大；而在30点平滑处理时得出的标准差与15点平滑程度时得出的标准差差别较小。

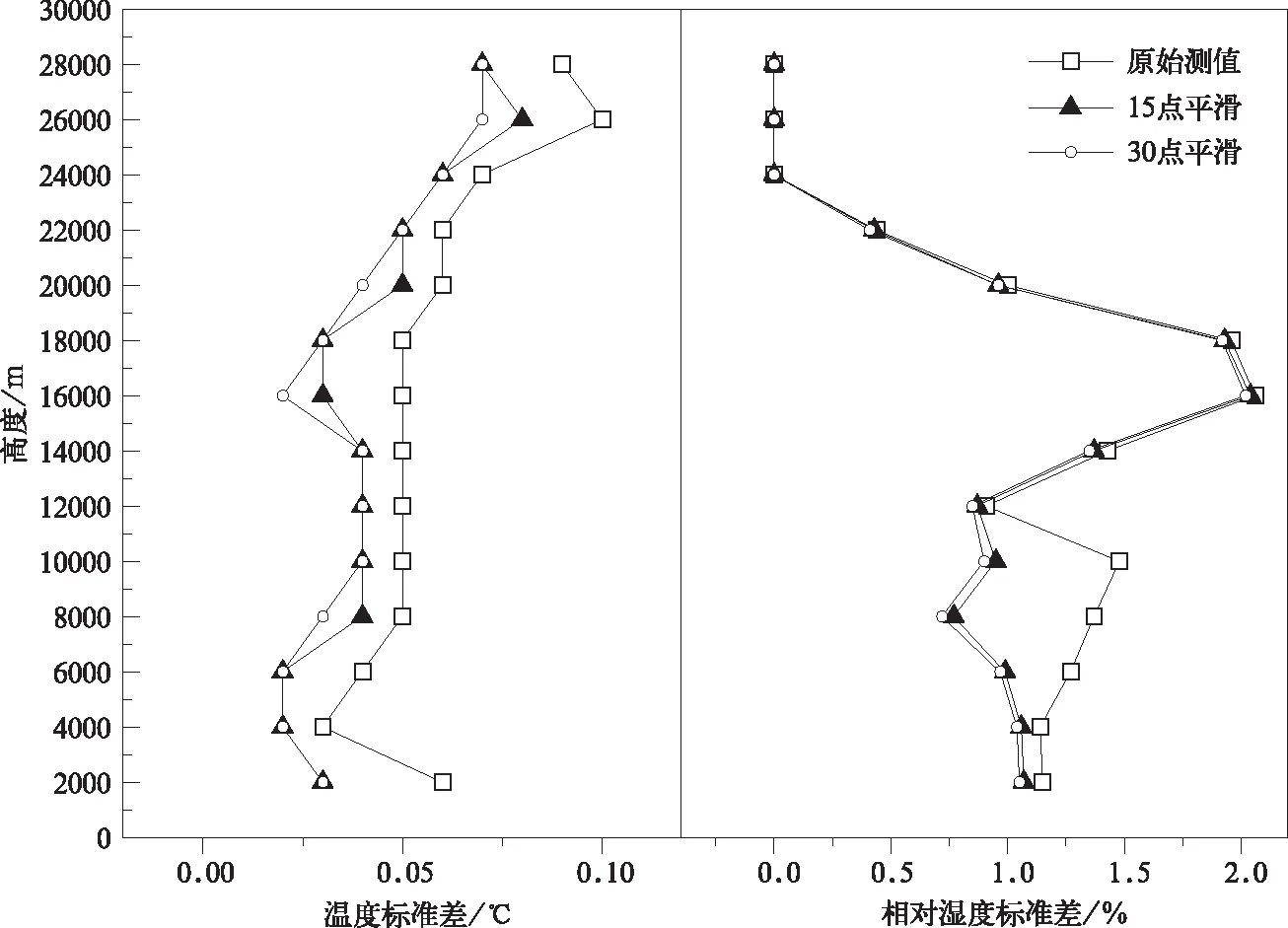
图4 不同的平滑程度下Vaisala RS92型GPS探空仪各高度层温度、相对湿度标准差Fig.4 Standard deviation of temperature and relative humidity of Vaisala RS92 GPS radiosondes by using different degree data smoothing methods

若探空仪Ⅰ′和探空仪Ⅱ′采用原始测值，探空仪Ⅲ′采用15点平滑，间接计算探空仪Ⅲ′的标准差(图5)。由图5可以看到，Ⅲ′的标准差明显偏大。当探空仪Ⅰ′和探空仪Ⅱ′原始数据采用30点平滑处理，探空仪Ⅲ′仍采用15点平滑，由间接计算得到的探空仪Ⅲ′的标准差也明显偏大(图略)。

为进一步比较平滑程度不一致对间接计算标准差的影响，图6给出利用直接计算方法得到的探空仪Ⅰ′与探空仪Ⅱ′的标准差。其中探空仪Ⅱ′保持15点滑动平滑，探空仪Ⅰ′分别采用原始测值、15点平滑和30点平滑处理(图6)。

可以看到，当2个探空仪原始数据平滑程度均适中时，即探空仪Ⅰ′与探空仪Ⅱ′均采用15点平滑，直接计算的标准差较小，当探空仪Ⅰ′采用不平滑处理或是30点平滑处理时, 探空仪Ⅱ′仍采用15点平滑，则直接计算的标准差明显增大许多。因此，如果再利用该标准差作为参考间接计算平滑程度没有变化的待测探空仪Ⅲ′的标准差，其结果也会有较大影响，只有平滑程度一致时，间接计算得出的标准差才最接近待测探空仪的实际标准差。同时由图6可见，平流层温度的标准差在平滑程度不同时变化很大，这就解释了中国阳江国际探空系统比对结果中不同国家的探空仪的温度在平流层处间接计算的随机误差出现明显差异的原因[21]。

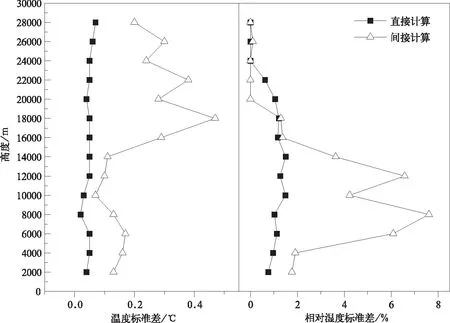
图5 3个Vaisala RS92型探空仪经过15点和30点平滑后各高度层温度、相对湿度标准差Fig.5 Comparison of standard deviation of temperature and relative humidity of Vaisala RS92 GPS radiosondes by using different data smoothing

图6 不同平滑程度对直接计算探空仪Ⅰ′和探空仪Ⅱ′各高度层温度、相对湿度标准差的影响Fig.6 Effects of different degree data smoothing methods on standard deviation of temperature and relative humidity of Ⅰ′ and Ⅱ′

6 结 论

本文通过对2007年6月和2008年6—7月国内GPS探空仪同步比对试验数据以及2010年中国阳江国际探空系统比对试验资料分析发现：

1) 秒级探空系统感应元件反应快，数据采样率高，但为了减少上升过程中气球摆动引起的探测要素波动，需要对原始探空测值进行平滑处理。如果对原始测值的平滑程度一致，可以利用间接计算方法获得待测探空仪的随机误差。如果对原始测值的平滑程度差异较大，则间接计算的随机误差会明显偏大。因此，现有的随机误差间接计算方法不能完全适用于秒级探空数据，特别是对于风、平流层温度和对流层相对湿度3个要素的随机误差的评估。

2) 为了获取某种型号探空仪的随机误差，建议将多个同型号探空仪挂在同一气球下进行同步比对试验，以避免作为参考的其他型号探空仪其自身的误差参与计算，影响待测探空仪的随机误差的估计。同型号探空仪同球施放的探空仪越多，获取的有效统计数据越多，随机误差的分析越准确。

3) 为了获取两种型号探空仪间的相对系统误差以及各自的随机误差，比对施放的方案中建议将两种型号探空仪(每种型号各2个或3个)挂在同一气球下进行同步比对观测，利用两种型号探空仪间的测量值差异统计相对系统误差，利用同种型号探空仪间的测量值差异分析该型号探空仪的随机误差。

4) 如果探空仪温、压、湿传感器的输出受测量电路影响小，也可以在同一探空仪上安放两个以上相同的传感器，同样可以减少施放代价并获取较多用于统计分析随机误差的比对数据。

致 谢：本文探空资料获取得到了中国气象局气象探测中心的大力协助，特此致谢!

[1] 黄炳勋.GZZ-7型探空仪热敏电阻温度元件的辐射误差和滞后误差.气象科学技术集刊,北京:气象出版社,1985:1-9.

[2] 黄炳勋.国内外常规高空观测技术发展近况综述.气象,2004，20(5)：3-9.

[3] Guo Yatian,Huang Bingxun,Hu Deyun,et al.Correction for Bias of Chinese Upper-air Measurements.WMO,TECO-2002,12(7),2002.

[4] 徐文静,郭亚田,黄炳勋.GTS 探空仪碳湿敏元件性能测试数据分析及相对湿度订正.气象科技,2007,35(3):423-428.

[5] 姚雯，马颖，徐文静.L波段电子探空仪相对湿度误差研究及其应用.应用气象学报,2008,19(3):356-361.

[6] 姚雯,马颖,黄炳勋,等.利用GPS定位资料分析L波段雷达测风性能.应用气象学报,2009,20(2):195-202.

[7] 姚雯,马颖.用GPS定位数据研究L波段雷达-数字探空仪系统的测高误差.气象,2009,35(2):88-93.

[8] 李伟,赵培涛,郭启云,等.国产GPS探空仪国际比对试验结果.应用气象学报,2011，22(4):453-462.

[9] 邢毅,张志萍,曹云昌,等.RS92型探空仪性能试验与分析.气象科技,2009，37(3):336-340.

[10] 李伟,邢毅,马舒庆,等.国产GTS1探空仪与VAISALA公司RS92探空仪对比分析.气象，2009，35(10):97-102.

[11] 马颖,姚雯,黄炳勋．59型探空仪与L波段电子探空仪温度和位势高度记录直接对比分析．应用气象学报,2010,21(2):214-220.

[12] 马颖,姚雯,黄炳勋.用初估场对比中芬探空仪温度和位势高度记录.应用气象学报,2011,22(3):336-345.

[13] 姚雯,马颖,王战,等.用数值预报初估场间接对比新疆两种型号探空系统.应用气象学报,2012,23(2):159-166.

[14] Ivanov A,Kats A,Kurnosenko S,et al.WMO International Radiosondes Comparison，PHASE 3，Final Report,WMO/TD-No.451，1991.

[15] Oakley T.Report by the Rapporteur on Radiosonde Compatibility Monitoring Part A:WMO Catalogue of Radiosondes and Upper-air Wind Systems in Use by Members.WMO/TD-No.886,1998.

[16] Reinaldo B da Silveira,Gilberto Fisch,Luiz A T Machado,et al.Executive Summary of the WMO Intercomparison of GPS Radiosondes.WMO/TD-No.1153,2003.

[17] Zhao Zhiqiang,Huang Bingxun.Some Step of Quality Control of Upper-air Network Data in China.WMO,TECO-2005,P3(4):2005.

[18] Li F.New Developments with Upper-air Sounding in China.WMO/TD-No.1354,Paper 2(1),2006.

[19] Kurnosenko S,Oakley T.Description and User Guide for the Radiosonde Comparison and Evaluation Software Package.WMO/TD-No.771,1996.

[20] Nash J,Smout R,Oakley T,et al.The WMO Intercomparison of Radiosonde Systems-Final Report.WMO/TD-No.1303,2006.

[21] Nash J,Oakley T,Võmel H,et al.WMO Intercomparison of High Quality Radiosonde Systems.WMO/TD-No.1580,2011.

Evaluation on the Random Error of Second Level Sounding Data

Yao Wen Ma Ying

(LaboratoryofLightningPhysicsandProtectionEngineering,StateKeyLaboratoryofSevereWeather,ChineseAcademyofMeteorologicalSciences,Beijing100081)

With the development of science and technology, the performance of sounding system，including the data acquisition rate, accuracy, reliability and automation are improved significantly. Comparison and statistical methods to estimate various errors are also needed to be improved. Relative system error and random error are concern variables of the sounding information users, errors evaluated by the reasonable method can reflect typical characteristics of error to same extent. So far, there have not a satisfactory standard radiosonde developed as a reference, relative system error and random error are obtained only through direct intercomparison simultaneously. The random error, it is not determined by dual-launching the same type of radiosondes because of the heavy workload. It is mainly used the indirect estimation method, that is the random error of the specify instrument used as a reference, and then the random error of unknown radiosonde is isolated from the variance between reference and unknown radiosondes. But whether the indirect calculation method of random error is suitable for the second level sounding data or not, the further discussion should be adopted. An overview of the random error is explained including the definition and determination method. And then two datasets are used to analyze the effect on the random error by different degree of data smoothing. One is the data of domestic GPS radiosondes comparison experiments in June 2007 and June-July 2008, the other dataset is the 8th WMO radiosonde comparison at Yangjiang China in 2010. The intercomparison analysis shows that the indirect calculation method of random error could not fully be applicable to the second level sounding data, especially for the estimation of random error of wind, temperature in stratospheric and relative humidity in tropospheric. The second level sounding data can detect the more detail caused by the swing of rising balloon, the raw data should be smoothed to reduce the impact of the above. If smoothing degrees of the original data compared are consistent, the indirect calculation method of random errors could be used suitably. The deviation is small, conversely, it might be problematical, which will produce large bias if it exists the difference in smoothing degree of the original data. In the scheme of direct intercomparision, in order to obtain the relative system error and random error of the different types of radiosonde systems, it is best to hang more than one of the same types of radiosonde in the same balloon to contrast synchronously, which can reduce the influence on evaluating the unknown radiosonde random error because of the own error of reference instrument. The more radiosondes of the same type are used, the more valid data could be obtained, the more accurate evaluation of random errors could be obtained.

random error; simultaneous intercomparison; degree of data smoothing

10.11898/1001-7313.20150509

国家自然科学基金项目(41105122)，国家重大科学仪器设备开发专项(2012YQ11020504)

姚雯,马颖. 秒级探空数据随机误差评估. 应用气象学报，2015，26(5)：600-609.

2015-03-04收到， 2015-05-19收到再改稿。

* email: yaowen@cams.cma.gov.cn