基于体积膨胀的固体推进剂粘弹性泊松比测量方法①

刘长猛,杨 轩,李念瑄,王 旭,吴 敏,张镇国*

(1.西安航天动力技术研究所 固体推进全国重点实验室,西安 710025;2.火箭军驻西安第一军事代表室,西安 710025)

0 引言

固体火箭发动机因其具有结构简单、维护方便、工作稳定、长期待命、启动迅速等特点,在导弹及航天动力系统中得到了普遍应用[1]。HTPB复合固体推进剂目前已在固体火箭发动机中得到广泛应用,其材料参数的准确性直接影响到药柱结构的安全裕度,甚至关系到发动机的工作成败。相关研究显示在内压载荷下,固体推进剂的粘弹性泊松比每相对变化1%,可导致药柱的应力-应变响应相对变化10%以上[2-3]。实际工程研制中,受测试手段、计算方法等因素限制,一般将固体推进剂的粘弹性泊松比作为常数处理,但随着导弹总体对固体发动机的性能要求越来越高,目前的粘弹性泊松比处理方法已经不能满足精细化设计的需求。因此,开展固体推进剂的粘弹性泊松比测试技术研究,准确揭示粘弹性泊松比的变化机理,对于支撑新一代固体火箭发动机研制具有重要意义。

国外早在20世纪60年代,SMITH等[4]便讨论了大变形条件下颗粒复合材料的体积变化与粘弹性泊松比的关系,并给出了粘弹性泊松比的计算公式。FARRIS[6]开展了推进剂拉伸过程中的体积膨胀率测量系列试验,但只将体积膨胀数据用于“脱湿”分析,并未将其用于讨论粘弹性泊松比的变化情况。国内方面,赵伯华等[7-9]推导出了拉伸松弛模量E(t)、体积松弛模量K(t)和粘弹性泊松比υ(t)之间的相互关系,并以E(t)、K(t)的实测结果,计算得到了一种改性双基推进剂的粘弹粘弹性泊松比。何铁山等[10]利用圆管发动机在固化降温后内孔的最大径向形变量,利用有限元计算程序拟合计算得到了药柱的粘弹性泊松比,但该方法成本较高,不适合于试件级测试。职世君等[11]推导得到了粘弹性泊松比随推进剂老化的变化规律,并将粘弹性泊松比引入老化参数,预估了某发动机装药贮存寿命。郑健等[12]采用接触测量方式获得了推进剂的横向应变,并结合其松弛模量间接得到了推进剂的粘弹性时变粘弹性泊松比。张晓等[13]通过准确测量载荷响应,利用有限元软件,对推进剂响应状态下的粘弹性泊松比进行了分段反演。申志彬等[14-15]推导了粘弹性泊松比的松弛型定义,提出了一种基于数字图像相关方法的固体推进剂粘弹性泊松比测量方法,能够将推进剂粘弹性泊松比的测量精度精确到千分位。李晔鑫等[16]利用快速建压试验系统模拟了低温下发动机点火升压过程,根据试验结果,反演得到了相应条件下的粘弹性泊松比。综上所述,固体推进剂粘弹性泊松比的理论研究已经较为成熟,但在测量研究方法方面主要为数字图像相关方法和数值反演法,其中数字图像相关方法未考虑试件形状因子对粘弹性泊松比的影响[8],数值反演法则需要研制圆管发动机,并开展固化降温试验,成本较高且缺乏明确的测量意义。尚缺乏一种可以不受试件形状因子影响的粘弹性泊松比测量方法。

本文搭建了一种基于体积膨胀的固体推进剂粘弹性泊松比测量系统,所测量的粘弹性泊松比不受试件形状因子影响,实现了固体推进剂粘弹性泊松比试件级的实时快捷测量,对固体发动机药柱结构完整性精细化分析具有重要实用意义。利用所搭建测量系统,开展了HTPB推进剂的粘弹性泊松比测试,获得了其在不同应变率及不同配方下的粘弹性泊松比变化规律。

1 测量系统及试验方案介绍

1.1 测量系统介绍

基于体积变化的固体推进剂粘弹性泊松比测量系统的核心在于获得试件受拉时的实时体积膨胀数据,根据体积膨胀数据再进一步分析其粘弹性泊松比的变化情况。本文参考FARRIS[6]的“脱湿”测试装置,搭建了固体推进剂粘弹性泊松比测量系统,其结构组成示意图如图1所示。该测量系统可以直接安装于现有拉伸机上,拉伸杆与拉伸机动横梁连接,由拉伸机动横梁提供位移载荷;试验腔室包含测试腔和参考腔两个腔室,两个腔室之间安装高精度压差传感器,用以测量测试腔和补偿腔之间的压差;推进剂试件两头在粘接夹具之后再装到测试腔内部的固定夹具上;参考腔用于提供气压参考基准并等于测试腔的初始气压值;为了高精度完成标定工作,专门设计了标定组件,标定组件主要由微调千分尺和微调内螺杆组成,通过拧动微调千分尺使内螺杆逐渐伸入测试腔,以达到改变测试腔体积的目的,拧入的距离可以由微调千分尺的刻度读取,该标定组件和测试腔连接处也设置了O型圈密封。测量系统实物如图2所示。

图1 测量系统的结构组成示意图Fig.1 Schematic diagram of measurement system1-Fixture;2-Specimen;3-Fixture;4-Micrometer;5-Pedestal;6-Displacement sensor;7-Moving beam of material testing machine; 8-Stretching rod;9-Internal screw;10-First pipe;11-Second pipe;12-Differential pressure transducer;13-Test chamber;14-Static beam of the material testing machine;15-Reference chamber.

图2 固体推进剂粘弹性泊松比测量系统Fig.2 Measurement system of viscoelastic Poisson's ratio of solid propellant

传统的拉伸试验一般采用标准哑铃型试件,但考虑到试验时其两端部分仍会出现体积膨胀,为了减少两端部分的影响。本文在哑铃型试件的基础上,切除两端部分,得到一种新型试件,并设计了匹配的夹具,传统哑铃型试件与新型试件及其配套夹具的效果图见图3,试件在测试腔中的装夹状态见图4。

图3 传统试件与新型试件及配套夹具对比Fig.3 Comparison between traditional specimen and new specimen and their fixture

图4 试件在测试腔中的装夹状态Fig.4 Clamping state of the specimen in the test chamber

1.2 测量原理

试验过程中,随着测试腔中的试件不断被拉伸,试件体积不断膨胀,测试腔内气体体积逐渐减小,气体压力逐渐升高,根据克拉伯龙方程[17]有

(p1+Δp)(V1+ΔV)=n1RT1=p1V1

(1)

式中p1为测试腔气体介质初始压强;Δp为测试腔内气体介质压强变化量;V1为测试腔气体介质初始体积;ΔV为测试腔内气体介质体积变化量;n1为测试腔内气体介质摩尔数;R为气体常数;T1为测腔内气体初始温度。

将式(1)进一步变换得到下式:

(2)

其中,参数k和c可以通过标定试验获得;Δp通过高精度光敏压差传感器直接测量得到。

根据文献[8],体积应变型粘弹性泊松比υ(t)的精确表达式为

(3)

其中,r为轴向应变速率,即

r=dε11/dt

(4)

则对于定速拉伸即r为常数的情况下,则有

(5)

式中的ΔV(ε11)值由式(2)获得。

根据式(5),可以看到推进剂的粘弹性泊松比与其体积膨胀率具有非常简约的微分关系,通过测量推进剂试件拉伸过程中的实时体积变化情况,即可计算得到实时的粘弹性泊松比变化情况,根据文献[8],基于式(5)得到的粘弹性泊松比精度可达3位有效数字。

1.3 试验方案介绍

本文主要研究常温常压下不同配方、不同应变率两个因素对HTPB推进剂粘弹性泊松比的影响规律。

试验考虑0.5、20、200 mm/min三种拉伸速率,试件总长为70 mm,则所对应的应变率分别为1.19×10-4、4.76×10-3、4.76×10-2s-1。采用三种HTPB推进剂试件,具体配方如表1所示,其中Al颗粒的粒径较小,粒径范围为10～30 μm,AP的粒径较大,粒径范围为100～300 μm。

表1 三种推进剂中各组分的体积分数Table 1 Volume fraction of each component of three propellants %

2 试验结果分析

2.1 推进剂拉伸过程中粘弹性泊松比典型变化规律

配方2在4.76×10-2s-1应变率下的典型膨胀率曲线和粘弹性泊松比曲线变化情况见图5。可以看到,粘弹性泊松比呈现出典型的S型曲线特征。应变较小时,粘弹性泊松比几乎保持不变,图5中应变从0增大到3.5%,粘弹性泊松比仅从0.499 0降低到0.497 4,该应变范围内试件的最大体积膨胀率为0.04%,表明细观尺度上推进剂中的AP、Al等增强体颗粒与HTPB基体的粘接界面还没有发生破坏;随着应变继续增大,推进剂的体积膨胀率开始显著增长,且增长速率越来越快,这表示在推进剂内部已经陆续出现“脱湿”,即增强体颗粒与基体的粘接界面逐步破坏,形成空穴、微裂纹等缺陷,粘弹性泊松比则表现为接近线性降低的特点;当推进剂内部的“脱湿”充分发展,随着应变继续增大,推进剂的体积膨胀率也近乎呈线性增长,这表示推进剂内部空穴增长速率达到了一个相对稳定值,此时推进剂的粘弹性泊松比接近下限,并保持相对稳定,对图5试验所使用的配方2推进剂来说,其粘弹性泊松比下限约为0.31,相对初始泊松比降低了38%。

图5 体积膨胀率与粘弹性泊松比的典型变化曲线Fig.5 Typical curves of volume dilatation and viscoelastic Poisson's ratio

2.2 应变率对粘弹性泊松比性能的影响

配方3在不同应变率下的体积膨胀率曲线见图6,对应的粘弹性泊松比曲线见图7。可以看到,粘弹性泊松比具有典型的率相关性,产生同样的应变,应变率越大,其粘弹性泊松比下降的越剧烈。结合图6可以看到,推进剂的体积膨胀率随着应变率的增大也逐渐增大,意味着其内部的“脱湿”损伤越厉害。

图6 不同应变率下的体积膨胀率Fig.6 Volume dilatation under different strain rates

图7 不同应变率下的粘弹性泊松比Fig.7 Viscoelastic Poisson's ratio under different strain rates

进一步发现,图7中在应变率为4.76×10-2s-1时,其末端粘弹性泊松比出现了几乎不变的现象。分析认为,推进剂内部颗粒的“脱湿”速率随着应变率的增大而增大,当应变率增加到某一临界值后,在试样被拉断前才会出现典型的“脱湿”速率达到上限不再增加的情况,即表现为体积膨胀随着应变增大几乎呈现线性增大,粘弹性泊松比几乎不变。

2.3 配方对粘弹性泊松比性能的影响

不同配方推进剂的体积膨胀率曲线见图8,对应的粘弹性泊松比曲线见图9。

图8 不同配方推进剂的体积膨胀率Fig.8 Volume dilatation of propellants with different formulations

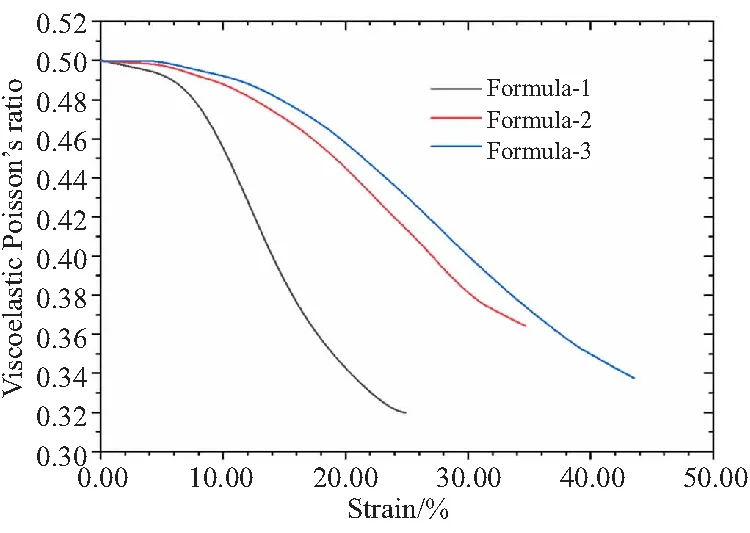
图9 不同配方推进剂的粘弹性泊松比Fig.9 Viscoelastic Poisson's ration of propellants with different formulations

由图9可以看到,粘弹性泊松比的变化情况与推进剂的配方关系密切,配方1的粘弹性泊松比下降的最快,这与其配方中粒径较大的AP的含量最高有关(AP含量达到了78%)。从图8中也可以看出,配方1对应的体积膨胀率也增大较快,结合文献[16]分析结论,“脱湿”首先在大颗粒界面发生,配方中AP的含量越高,其内部“脱湿”越容易发生,粘弹性泊松比越容易下降,相应固体颗粒对基体的增强能力越容易损失。而配方2和配方3的体积膨胀曲线和粘弹性泊松比变化曲线差别均较小,配方3的粘弹性泊松比下降的最慢,配方2和配方3中粒径较大的AP含量相同,但配方3中粒径较小的Al颗粒含量略高于配方3。

分析认为,推进剂中Al颗粒粒径较小,不容易发生“脱湿”,适度提高推进剂中的粒径较小的Al颗粒含量,可以利用其粒径较小不容易发生“脱湿”的特点,增强基体的力学性能,具体到粘弹性泊松比性能则表现为其随应变的降低速率减小。

3 结论

(1)HTPB推进剂的粘弹性泊松比具有明显的率相关特性,应变率越大,其粘弹性泊松比下降的越剧烈,也表明其内部的“脱湿”损伤越剧烈;

(2)HTPB推进剂的粘弹性泊松比变化规律与配方密切相关,配方中大颗粒的AP的含量越高,其内部“脱湿”越容易发生,粘弹性泊松比越容易下降,相应固体颗粒对基体的增强能力越容易损失;

(3)本文建立的测量系统可以实现固体推进剂试件级的粘弹性泊松比实时快捷测量,粘弹性泊松比测量数值的有效位数达到3位,且所测量的粘弹性泊松比不受试件形状因子的影响,可以为固体火箭发动机精细化设计提供有力支撑。