一种适用于柔性接头摆动寿命的预估方法①

潘 娟,万 诺,2*,郗冰洁,李 冰,屈转利,王 才,史宏斌,效天祺

(1.西安航天动力技术研究所,西安 710025;2.固体推进全国重点实验室,西安 710025;3.西安航天化学动力有限公司,西安 710025;4.中国人民解放军火箭军装备部驻西安地区第一军事代表室,西安 710025;5.西交利物浦大学,苏州 215000)

0 引言

固体火箭发动机喷管柔性接头可以通过连续全周大摆动提供偏向力,发动机推力控制系统的可靠性往往取决于喷管柔性接头的摆动可靠性。柔性接头不同振幅、频率的摆动形式组合能起到推力控制的作用,改变发动机的飞行姿态。柔性接头是由前后法兰、弹性件和增强件同心交替粘接组成的一个完整部件,在实际工作中要承受来自发动机燃烧室压强、喷管摆动时不对称的作动力及飞行过程中的加速度等复杂载荷[1-3]。在长期贮存、检测和工作过程中柔性接头会因多次机械载荷作用发生疲劳失效。因此,研究柔性接头不同摆动形式下的寿命具有重要意义。

柔性接头摆动时弹性件会发生拉、压、剪、拉剪、压剪等形变,弹性件或界面间应力集中区域易发生摆动损伤,多次摆动时损伤积累最终会导致柔性接头疲劳破损。在探究柔性接头摆动寿命时应首先关注柔性接头摆动损伤情况。刘勇琼等[4]利用有限元方法研究了柔性接头弹性件与增强件间界面上的最大拉应力及层间剪应力的分布情况。曹翠微等[5]通过仿真获得了不同容压下柔性接头摆动时弹性件表面的应力-应变分布情况。安春利等[6]模拟柔性接头的冷态摆动过程获得弹性件表面的应力,发现柔性接头粘接面破坏的主要因素为轴向柯西主应力过大。王春光等[7]仿真发现最外层弹性件的弹性比力矩最大,并发现低压摆动时弹性件表面的剪应力较大。在研究柔性摆动时,弹性件承受的较大拉应力或剪应力会导致柔性接头弹性件摆动损伤。此外,层间剪应力过大也会引起粘接界面破坏,这是导致柔性接头摆动失效的另一原因。在探究柔性接头摆动寿命时,主要关注弹性件受到的拉应力、剪应力及粘接界面的损伤情况。在柔性接头寿命预估方面,李太安等[8]使用ANSYS nCode-DesignLife对柔性接头弹性件进行疲劳分析,获得了柔性接头的疲劳寿命及破坏时柔性接头内部临界应力、应变等;张天华等[9]采用有限元模拟与橡胶疲劳实验相结合方法,有效预测了硫化天然橡胶(NR)哑铃型试样的疲劳寿命;刘建勋等[10]针对汽车减震元件的橡胶部位疲劳破坏问题,通过试验及仿真模拟实现橡胶产品结构的疲劳寿命预测。大部分学者的研究以分析橡胶构件的力学性能或疲劳寿命为主,对金属-橡胶层叠结构的疲劳损伤研究较少,尚未对柔性接头疲劳摆动寿命的预估计算。

本文基于疲劳损伤理论,探究不同应变幅值的载荷谱对柔性接头寿命的影响,通过仿真结果与试验结果对比,形成柔性接头疲劳摆动寿命预估方法。利用该方法可以快速预估柔性接头的摆动寿命,节省试验时间和成本,为柔性接头工作可靠性评价提供参考。

1 疲劳寿命预估原理

柔性接头摆动时产生疲劳裂纹的弹性件表面一般处于二轴平面应力、三向应变状态。疲劳裂纹的发生与承受应变、应力的平面有关,须考虑二轴平面应力的影响。

在多轴应变分析的疲劳理论[11]中最常采用最大主应变准则,认为疲劳裂纹产生于发生最大主应变幅的平面上。计算弹性应变εe、塑性应变εp、总应变ε分别为

(1)

(2)

式中E*为循环弹性模量(等于橡胶弹性模量E);K′为循环硬化系数;n′为循环硬化指数。

数学表达一般要把应力-应变同时放大2倍方便计算,因此应变幅-寿命关系为

(3)

式中σf′为疲劳强化系数;b为疲劳强化指数;εf′为疲劳延性系数;c为疲劳延性指数;2Nf为载荷半循环次数。

此外,还有最大剪应变准则,该准则在计算中认为疲劳裂纹产生于发生最大剪应变幅的平面上。适用于非金属材料疲劳寿命分析,公式推导得到:

(4)

式中 Δγ为剪应变。

在损伤积累过程中需应用平均应力修正,也基于式(4)计算出允许的半循环数2Nf。针对橡胶疲劳寿命分析有如下两种修正方法:

(1)Smith-Watson-Topper法。平均应力修正曲线认为疲劳寿命与应变幅、最大应力的乘积有关,σmax为迟滞环最大应力。公式如下:

(5)

(2)Morrow法。平均应力修正曲线则更为简单,σm为迟滞环平均应力。公式如下:

(6)

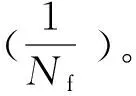
2 疲劳寿命预估方法确定

现代疲劳理论认为某点的应力-应变历程会引起橡胶材料疲劳破损,并以试样裂纹达到设定评估尺寸所承受的循环载荷次数来定义疲劳寿命。疲劳寿命预估中以有限元仿真的应力-应变结果为基础,计算该应变状态下单次循环加载造成的损伤,对损伤积累达到预置的裂纹宽度(一般为1 mm)获得疲劳寿命。

由于柔性接头结构复杂、制作成本较高,例行的柔性接头摆动寿命试验耗时久,考虑界面损伤问题提出一种具有普适性的柔性接头摆动寿命预估方法。FE-Safe是建立在有限元分析结果基础上的专业疲劳寿命计算软件,在金属和非金属领域均有广泛应用。通过有限元仿真获得试样在单个循环应变下的应力-应变分布情况,将仿真结果.odb文件导入FE-Safe/Rubber中,输入本构模型参数、S-N曲线,选择合适的疲劳算法和修正公式,按历程积累多次循环载荷下的损伤,得到试样的寿命预估结果。

2.1 柔性接头摆动寿命表征试样的选取

根据国内外对柔性接头表征试样的分析,本文在研究柔性接头弹性件摆动损伤时,弹性件承受拉应力采用哑铃试样表征,弹性件承受剪应力及橡胶-钢界面损伤情况采用四重片试样表征。

哑铃试样(Q/Gb 177—2003)如图1所示。柔性接头摆动时,弹性件发生剪切大变形,处于双向应力状态。利用平面应力状态研究法,根据柔性接头工作时的摆动角度,获得应力最大点的各应力状态可以计算出该点的正应力。在进行哑铃试样仿真时,以承受拉应力代替正应力,从而获得弹性件的预估寿命。

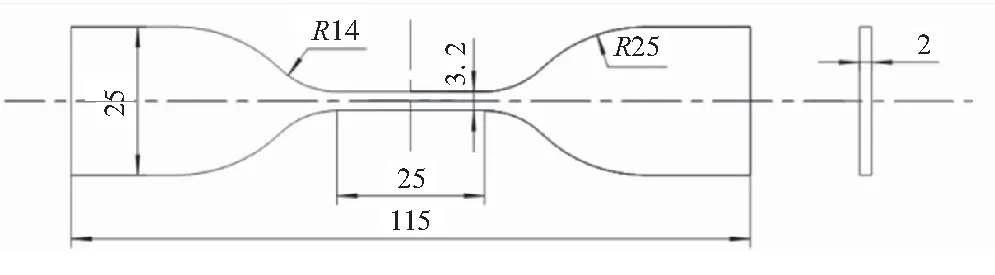
图1 哑铃试样(单位:mm)Fig.1 Dumb-bell specimen(Units:mm)

由于柔性接头为弹性件-增强件叠加结构粘接界面多,接头摆动时的界面损伤情况会影响其寿命。层间剪应力是导致界面损伤的主要因素,选用四重片试样(Q/Gb 58.1—1987)如图2所示,进行橡胶剪切形变仿真,获得橡胶受剪后的应力-应变情况,并分析界面损伤对试样疲劳寿命的影响。

图2 四重片试样(单位:mm)Fig.2 Four-piece specimen(Units:mm)

2.2 试样仿真参数设定

柔性接头一般在摆动时橡胶材料的剪切变形量100%～300%,考虑极端情况剪应变可达600%。采用该天然橡胶开展应力-应变关系试验[13-14],获得数据及拟合情况如图3所示。考虑模型拟合情况及计算收敛性,选用Yeoh本构模型描述弹性件的应力-应变关系。Yeoh模型参数及其他有限元仿真设定情况见表1。

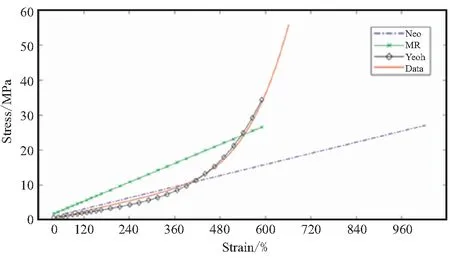
图3 天然橡胶剪切应力-应变关系Fig.3 Shear stress-strain curves of rubber

表1 有限元仿真参数设定Table 1 Main parameters of FEM

研究疲劳问题的S-N曲线方法(S为施加的应变幅值,一般以正弦波的循环应力或交变应力为主;N为断裂时的疲劳周数)简述如下:试验通常在一定频率、恒定振幅和一定的最小与最大载荷比R下进行,以获得断裂时的疲劳循环总周数。

本试验中,四重片结构中间钢层为受力点,根据不同拉伸量获得不同应变,其中L0为钢层的初始预设拉伸量,L为最大拉伸量。试验采用Zwick疲劳试验机,可加载50 Hz频率以内应变,对四重片试件进行预设应变后恒频率拉伸。采用四重片试样进行100%～400%应变条件下的循环拉伸,记录断裂次数如表2所示。

表2 天然橡胶的S-N曲线试验数据Table 2 S-N curve experimental results of rubber

试验获得的Nf为断裂寿命的1/2,根据平均应力修正法在后期计算中FE-Safe输入的N即为Nf的2倍。在软件中绘制出天然橡胶的S-N曲线(如图4所示),其方程拟合形式采用适合非金属疲劳寿命的三参数经验公式[15]:

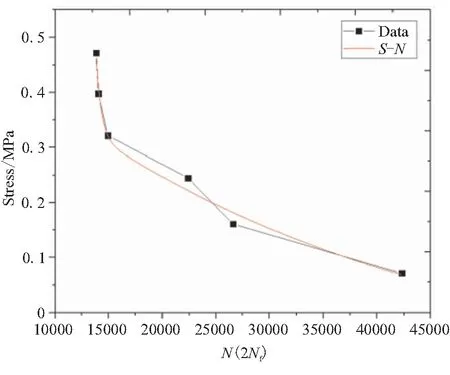
图4 S-N曲线Fig.4 S-N curves

N(S-S0)m=D

(7)

式中S0近似为疲劳极限;m、D为试验常数。

根据表2获得实验数据拟合幂函数曲线,得到试验常数m=0.697 8,D=7563。适应于天然橡胶材料的疲劳寿命预估的S-N曲线三参数公式为

N(S-S0)0.6978=7563

(8)

S-N曲线获得的方程和相关参数表征了材料的疲劳性能,在后续仿真计算中作为特性参数输入可以预估不同应力、应变条件下试件的疲劳寿命。

橡胶材料的本构模型参数和S-N曲线共同组成了适合本文计算模型的橡胶材料数据包,试件仿真疲劳寿命预估均采用该数据。在寿命预估时,试样三维模型的分析实体Subgroup设定为Whole,表示对所有单元整体结构进行分析计算。

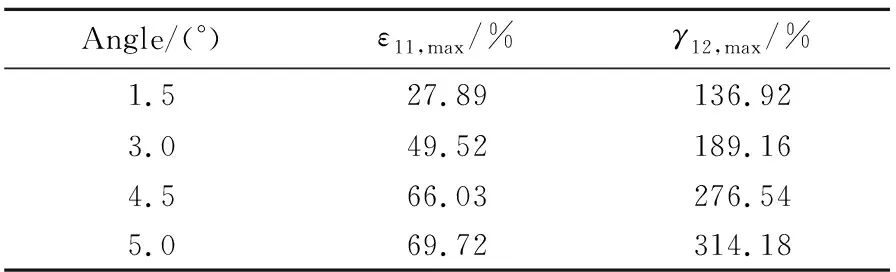
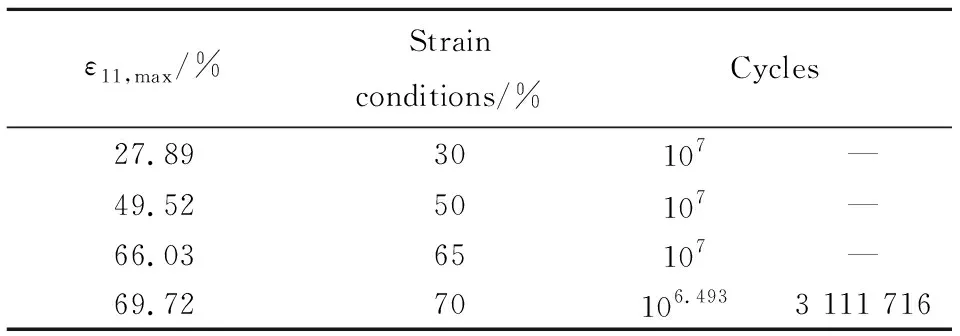
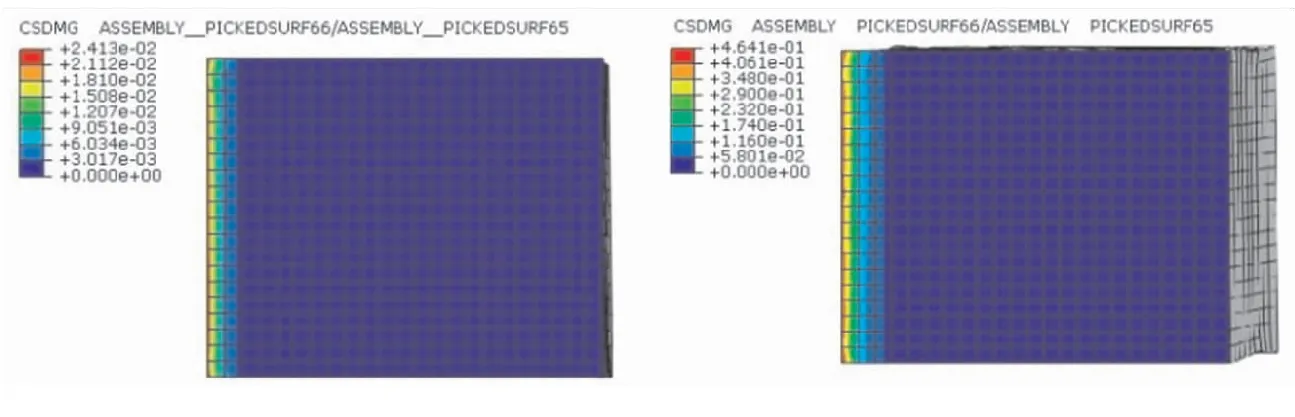
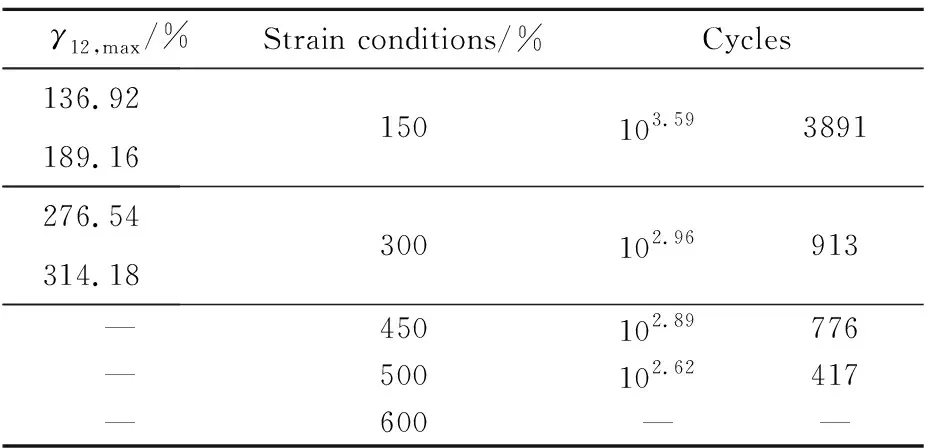
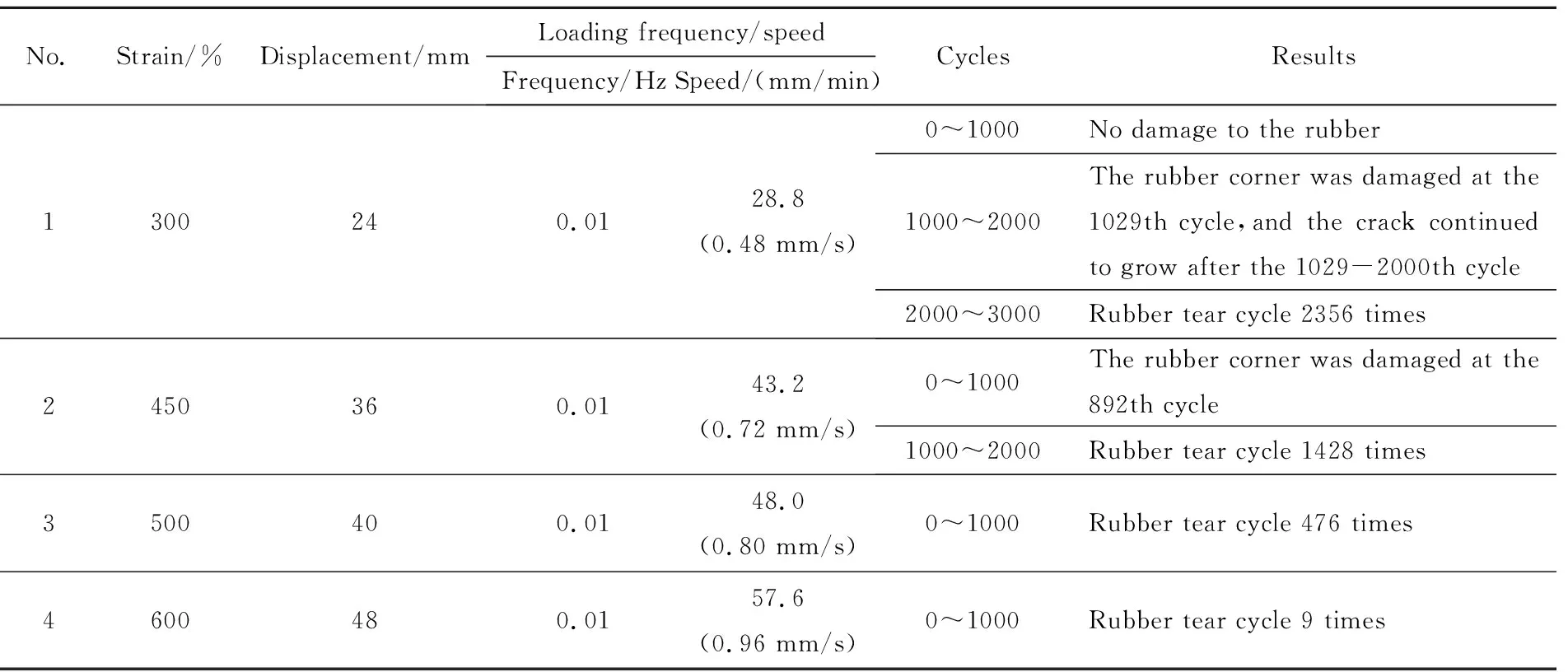
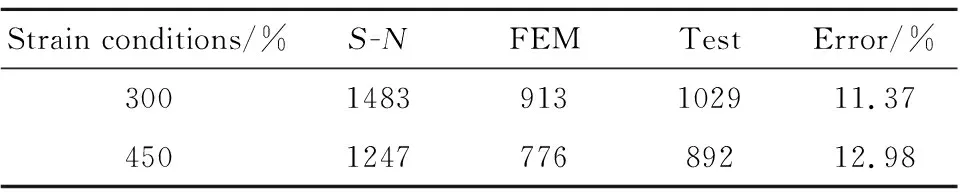
由于哑铃试样主要承受循环拉伸载荷,参考文献[11]中天然橡胶材料受拉的应变-疲劳寿命S-N曲线,预估时选择Principal Strain最大主应变法求解,采用简单的Morrow法进行平均应力修正,残余应力均为0。由于四重片橡胶试样的橡胶片主要受剪应力,采用双轴应变疲劳最大剪应变法(Max Shear Strain-Morrow)求解,钢材料结构单元选择Principal Strain-Morrow。试样表面精度对寿命也存在影响,Rubber单元的表面精度设定为0.25 μm

2.3 试样疲劳寿命预估工况的选取

在柔性接头疲劳寿命预估时,摆动不同角度弹性件单元会发生不同程度形变,产生不同的主应变和剪应变。以柔性接头摆动1.5°、3.0°、4.5°、5.0°为工作条件,通过有限元仿真获得靠近前法兰弹性件的主应变ε11。弹性件层间径向剪应变过大是导致界面脱粘的主要原因,仿真获得不同摆角下径向向剪应变γ12。获取不同摆角下弹性件的最大主应变、剪应变见表3,分别取近似值作为哑铃试样、四重片试样疲劳寿命预估的应变加载条件。

表3 弹性件最大主应变ε11,max、最大剪应变γ12,maxTable 3 ε11,max and γ12,max of rubber sheet

2.4 哑铃试样疲劳寿命的预估

分析某喷管柔性接头摆动1.5°～5°应变情况,按最大主应变对哑铃试样施加拉应变,哑铃试样载荷以先拉伸再恢复形变为一个循环进行有限元仿真,获得不同时刻的应力-应变情况。仿真得到寿命预估结果如表4所示,前3组由于应变小摆动107以上橡胶件仍不会出现裂纹,认为该条件下达到了无限寿命。

表4 哑铃试样疲劳寿命预估结果Table 4 Life calculation result of dumb-bell specimen

对哑铃试件应变为70%进行分析,该条件下的寿命预估云图如图5所示,在云图中预估寿命是以10的指数形式表示,发现最易发生疲劳失效部位为中间细长结构与扩张部分相连处。

图5 哑铃试样寿命预估云图Fig.5 Life expectancy contour of dumb-bell specimen

2.5 四重片橡胶试样疲劳寿命预估

本节采用四重片试样表征界面性能,预估试样在不同剪切应变下的寿命。柔性接头摆动1.5°～5°时,选取对应的剪切应变近似值为150%、300%进行仿真,为提高安全裕度增加450%、500%、600%应变的疲劳寿命预估。建立如图2四重片试样模型,按2.2节设定参数,在中间钢结构施加循环载荷,胶层界面采用接触面损伤模型计算[16-17],获得一个加载循环下试样的应力-应变及损伤结果。

由于四重片试件在承受循环剪应力时上下左右橡胶片受力情况一致,取单片橡胶为研究对象,在不同应变条件下,四重片试样橡胶片与钢结构间的接触面的损伤情况如图6所示。接触面的损伤程度用CSDMG表示,CSDMG损伤参数为0表示界面无损伤,1表示界面完全脱粘。由图6能看出,橡胶片边缘处为胶层损伤裂纹萌生位置,150%应变下胶层几乎无损伤,300%应变条件下,胶层的最大损伤参数不到0.5。450%和500%应变条件下,胶层的损伤参数达到0.6以上。600%应变条件下局部损伤参数达到1,一次循环加载就能导致局部胶层破损。随着应变的增大,胶层的损伤单元数增加,损伤面积扩大,且最容易发生胶层脱粘的位置相同。

(a)Strain 150% (b)Strain 300%

(c)Strain 450% (d)Strain 500% (e)Strain 600%图6 四重片试样损伤情况Fig.6 Interface damage of four-piece specimens

获得150%～500%不同应变下的疲劳预估如表5所示。600%应变过大,单次循环加载下胶层产生损伤,无寿命预估结果。对比表5不同剪切应变下的预估寿命结果发现,剪切应变越大,获得的四重片试样预估寿命结果越小。

表5 四重片试样寿命预估结果Table 5 Life calculation result of four-piece specimen

四重片试样加载应变300%、450%时,可视化寿命结果云图如图7所示。发现贴近中间层钢结构的界面最易发生破坏,该处能承受循环加载次数最小。

(a)Strain 300% (b)Strain 450%图7 四重片试样寿命预估云图Fig.7 Life expectancy contours of four-piece specimens

2.6 仿真结果分析及试样筛选

对比哑铃试样与四重片试样在相同摆角下的仿真寿命预估结果,发现四重片试样的预估寿命明显低于哑铃形试样。相同摆角下弹性件层间剪切应变导致的界面损伤对柔性接头疲劳寿命影响更大。因此,对柔性接头的寿命预估研究应以四重片试样进行表征。柔性接头摆动试验时,疲劳破损一般发生于全周期大摆角摆动情况下,分解运动后近似为橡胶剪切变形,四重片试样应用于疲劳试验更符合柔性接头摆动的试验形式。

3 四重片试样剪切疲劳试验

3.1 疲劳试验方法

剪切疲劳试验采用四重片结构,形状及尺寸如图2所示,中间层钢结构两端圆孔为试验机夹持器加载位置。在试验中,取形变量与橡胶厚度比值作为剪切应变量ε的近似值:

式中 Δl为线性位移;h为橡胶结构厚度。

试验采用Zwick疲劳试验机(如图8所示),可通过自主编程设定加载应变大小、调节加载频率、改变加载波形等。通过编程加载模拟柔性接头工作时橡胶件形变状态,以获得更加符合实际工况的柔性接头疲劳摆动寿命。

图8 疲劳试验机Fig.8 Fatigue tester

3.2 疲劳试验步骤

剪切疲劳试验加载时为一端固定,一端夹持器拉着试样中间层圆孔处进行往复运动。如加载300%应变时,夹持器一端固定,一端轴向位移24 mm,按原行程卸载至0,按加载-卸载为一循环,以此往复循环加载至橡胶材料发生疲劳破损,如图9所示。试验过程中要求平稳加载,夹持器按0.01 Hz匀速线性移动。在试验中记录橡胶破损时的循环加载次数,继续加载直至橡胶结构撕裂终止试验,描述试样损坏过程。

图9 试件夹装情况Fig.9 Installing state of the test piece

3.3 疲劳试验结果

在四重片剪切疲劳试验的4组试样具体加载要求及获得的疲劳循环次数见表6。试验结果以1000组循环拉伸分组进行拉伸结果描述,记录开始出现破损和橡胶完全撕裂的循环次数。试验完成后,4组四重片试样橡胶结构的撕裂状态如图10所示。

表6 试验条件及结果Table 6 Test conditions and results

(a)Strain 300% (b)Strain 450% (c)Strain 500% (d)Strain 600%图10 橡胶破损情况Fig.10 Pictures of damaged rubber

对比分析4组四重片剪切疲劳寿命试验结果,随着应变增加,橡胶结构的剪切疲劳寿命逐渐减小,但开始出现破损的位置几乎相同。300%应变条件下橡胶仍能在加低频载荷下保证千次以上循环加载才开始出现裂纹。至2356次循环橡胶完全撕裂。在柔性接头实际工作中,只有弹性件出现贯穿性裂纹,导致柔性接头漏气才会失效,故而根据试验结果300%应变情况下认为柔性接头能全周期大摆动安全工作2000次以上。第二组试验进行450%应变循环时,892次循环橡胶开始破损,1428次橡胶撕裂。500%应变条件下试验橡胶仍能正常工作476次,600%应变条件下由于应变过大,弹性件只能正常工作9个循环。

根据表6试验结果可以认为,300%应变条件下的柔性接头摆动寿命符合设计要求。当偶尔发生更大摆角摆动橡胶剪切应变达到500%时仍能安全工作476次,不会导致任务失败。当应变达到600%时,柔性接头很容易发生撕裂破损漏气,柔性接头为发动机俯仰偏航提供侧向力时摆动一定要处于弹性件600%剪切形变状态以内。

3.4 四重片剪切疲劳仿真与试验结果分析

仿真得到的寿命预估结果与试验中是裂纹刚刚萌生状态相对应,所以四重片剪切试验测试结果中300%、450%应变条件下开始出现破损的循环次数与四重片试样仿真预估寿命对比如表7所示,分别为根据S-N曲线预估寿命、使用有限元计算方法获得的预估寿命以及疲劳试验结果。

表7 寿命预估结果与试验结果对比Table 7 Comparison of life predictions with test results

对比S-N曲线预估结果与试验结果情况,S-N曲线预估循环寿命大于试验结果,这是因为S-N曲线仅考虑材料的疲劳性能,忽略材料受力形式、界面损伤等影响获得的预估寿命,这种预示方法简单,结果相差较大。

通过仿真与试验结果的情况对比,可以确定对于四重片结构橡胶寿命预估的结果误差在13%以内,误差较小,认为该寿命预估方法是可行的,且仿真结果可作为疲劳摆动测试的参考。

在仿真过程中,由于模型结构和材料参数能自主设定,复杂结构可以通过该仿真方法获得预估寿命,会节省试验时间,节约试验成本。在柔性接头摆动寿命研究时,可采用该方法进行寿命预估,为柔性接头摆动测试提供参考,从而指导柔性接头结构设计。

4 结论

本文通过分析固体火箭发动机喷管柔性接头摆动情况,对柔性接头弹性件和粘接界面的表征件开展疲劳摆动仿真计算、剪切疲劳试验,完成摆动寿命预估研究,得到如下结论:

(1)根据天然橡胶预置应变疲劳循环试验得到了材料的S-N曲线,根据三参数公式获得不考虑受力形式、界面损伤的预估寿命。

(2)根据柔性接头摆动时受载荷情况,对哑铃结构和四重片结构分别进行寿命预估仿真,发现应变越大,界面损伤程度越大,试样可以承受的循环载荷次数越少。通过两种试样寿命预估结果对比,选取四重片结构作为柔性接头的摆动疲劳特性研究的表征试样。

(3)采用四重片试样进行0.01 Hz下300%～600%剪切应变疲劳寿命试验,发现试验寿命结果与预估寿命结果误差在13%以内,从而验证了本文提出的寿命预估方法的正确性。

(4)通过对四重片试样疲劳寿命的研究,形成了适用于柔性接头绕摆心周期摆动寿命预估的研究方法,可为摆动测试提供参考。