面向高筋筒壳的结构优化设计和承载规律研究①

王法垚,马祥涛*,张登宇,朱英杰,郝 鹏,王 博

(1.大连理工大学 工程力学系,工业装备结构分析国家重点实验室,大连 116024;2.北京宇航系统工程研究所,北京 100076)

0 引言

加筋结构因其高比强度、比刚度等显著优势,常被用于如贮箱、各级间段等火箭的主体结构作为主承力部件。加筋筒壳结构占运载火箭干重极高,因此如何设计性能更加优秀的加筋壁板构型一直是各国航天工程师密切关注的核心问题之一。

国外得到广泛应用的加筋形式主要为蒙皮桁条、正置正交网格加筋筒壳、三角加筋筒壳及蜂窝夹层结构等。而我国的长征系列运载火箭经历了多阶段的连续发展,箭体直径从最初的2.25 m直径(CZ-1)增加至3.35 m直径(CZ-2C),进一步增加至5 m直径(CZ-5)。筒壳结构的构型形式也不断丰富,从最初的大面积采用蒙皮桁条结构发展至化铣斜置正交网格壁板、机铣正置正交网格壁板以及三角网格加筋[1]等。从国内外火箭结构构型的发展过程不难看出,随着材料与工艺水平的进步,也逐渐会涌现出更加适合需求的新一代结构构型。随着我国航天事业的稳步推进,以中国空间站、载人登月、火星探测及深空探测等为代表的重大航天工程正在陆续展开。重型运载火箭作为我国系列重大航天工程的基础,921登月火箭和CZ-9两款重型火箭[1-3]的型号研制工作也正在进行。箭体主承力舱段直径达10 m 级的CZ-9重型运载火箭,其轴压载荷将达4000 t级[4],主承力舱段将大量采用整体加筋、框桁加强的薄壁筒壳,以满足承载要求。为满足重型火箭型号“承载重型化、结构轻量化”的设计需求,火箭主体结构也亟需在保证服役可靠性的前提下进一步提升其承载效率。但是传统的蒙皮桁条、网格低筋等筒壳构型将无法满足大直径、大载荷加筋筒壳所带来的高承载效率要求。目前,随着国内在高精确挤压成形[5-9],金属增材制造[10-11]方面的快速进步,低成本、批量制造筋条高度大于50 mm 的大尺寸高筋筒壳结构也很快将成为现实,即将突破传统厚板铣削等工艺对于加筋壁板的筋高约束。这种高筋筒壳结构为下一代运载火箭筒壳选型提供了新的可能性,高筋筒壳有望凭借其高承载效率、强抗弯、抗侧向扰动能力以及强抗缺陷能力等优势,为下一代箭体筒壳选型提供支撑。因此,亟需面向型号的高承载效率需求,探究高筋筒壳构型的承载潜力,为新一代火箭结构提供参考。

伴随着航天筒壳结构的“轻质高承载”需求,国内外对薄壁结构构型的分析、设计及相关研究也显得愈发重要。其中,王博等[12-13]面向超大直径加筋筒壳结构提出了一种基于渐进均匀化的快速分析方法,并面向开口补强需求开展了结构尺寸-布局一体化设计。马祥涛等[14-15]基于不完全折减刚度法对加筋筒壳开展了考虑缺陷容忍性的快速优化设计。董曼红等[16]分析了网格加筋筒壳结构在不同工况下承载能力的变化规律,可进一步推导工程计算方法。梁珂等[17]将Koiter法与Newton弧长法结合,实现了网格加筋筒壳的承载稳定性特性分析。杨蓉等针对正交加筋筒壳和三角加筋筒壳开展了数值和实验研究,表明三角加筋筒壳承载能力要优于正交加筋筒壳[18]。王志祥等[19]针对蒙皮桁条结构开展了基于后屈曲分析的轻量化设计。吴栋等[20]基于Kriging代理模型和分步优化方法针对蒙皮桁条结构开展了优化设计,结果表明“Π”形桁条承载效率更高。郝鹏等[21]针对蒙皮桁条的减轻孔形状开展了优化设计,有效提升了结构承载效率。FAN等[22]基于能量壁垒方法对加筋筒壳开展了优化,实现了承载能力及抗缺陷能力的同步提升。TIAN等[23]采用振动相关技术实现了圆柱壳的快速优化设计。王博等[24]和乔丕忠等[25]对加筋筒壳结构的优化设计进行了全面的评述。但是上述对加筋筒壳开展的结构设计研究主要针对筋条高度低于30 mm且密布筋格的网格低筋筒壳或基于多部件焊接或铆接的蒙皮桁条筒壳结构,仍缺乏以新型高筋筒壳为研究对象的结构优化设计研究工作,导致高筋筒壳结构在优化设计及承载规律方面尚无较为全面的阐述。因此,亟需开展面向高筋筒壳的优化设计和承载规律研究。

本文介绍了加筋筒壳结构的承载力分析方法,以及包含聚类分析和斯皮尔曼相关性分析的结构承载规律研究方法,并以5 m直径筒壳结构为例,面向多种加筋构型,采用加点优化方法开展结构优化设计,对比不同构型的承载效率;基于优化结果及样本点数据,探究结构构型参数分布规律。

1 方法论

为探究加筋筒壳结构的承载规律,本研究在分析优化阶段拟采用显式动力学方法求解加筋筒壳结构的承载能力,在承载规律分析阶段采用斯皮尔曼相关性分析方法和聚类分析算法对加筋结构的构型参数分布开展数据分析。

1.1 加筋筒壳承载能力高精度分析方法

显式动力学方法是一种基于显式时间积分的非线性分析方法,可获得筒壳结构的极限承载力并且准确地模拟其后屈曲行为。其控制方程如式(1)所示:

(1)

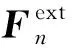
在给定初始增量步动力学状态a0、v0、u0后,基于显式的中心时间积分逐步推导下一个时间增量步的动力学状态。具体如下:

(2)

控制方程采用显式格式,故控制方程为条件收敛,收敛条件为

(3)

其中,

(4)

式中Le为结构单元的最小特征尺寸;cd为材料的波速。 从式(3)可发现,显式动力学的计算效率与所分析模型的最小单元尺寸相关,尤其是当模型中由于单元畸形或结构局部尺寸较小时,会导致模型的等效特征尺寸极小,从而使得整体的分析效率极为低下,对于复杂加筋筒壳,一般通过模型降阶、质量缩放等手段对显式动力学分析过程进行加速。

对于优化设计来说,显式动力学的优势一方面在于高保真度,其可以通过时域迭代精确模拟结构的准静态加载过程与后屈曲路径;另一方面在于可求解性。由于采用显式时间积分格式,因此该方法基本不会出现收敛性问题。但其劣势也很突出,由于显式格式的时间积分需要大量迭代导致其极其耗时,因此本文采用了基于代理模型的加点优化来提升优化效率。

1.2 斯皮尔曼相关性分析方法

斯皮尔曼相关性分析方法(Spearman Correlation Coefficient,SCC)是一种广泛用于测量变量单调相关性的统计学方法,该方法主要基于数据排序等级来评估向量间单调性关系的强度。经过分析后可以根据相关系数r和P值评估变量间单调性的相关程度。其中,相关系数r的取值范围为[-1,1],r为正代表向量的单调性为正相关,r为负数则代表向量的单调性为负相关;r的绝对值越接近1则代表相关性越强,越接近0则代表相关性越弱。P值为评估相关程度计算结果的显著程度系数,代表原假设成立的概率,在斯皮尔曼相关性分析中则表现为“向量间不存在单调相关性”这一假设的概率,因此P值越小则相关性的显著性越强,一般取0.05作为判断阈值,即P<0.05时则认为有显著证据接受相关性计算结果,当P>0.05时则认为不存在显著证据接受相关性计算结果。

1.3 聚类分析算法

聚类即按照某个特定标准把一个数据集分割成不同的类别,使得某一个类别内部的元素的某种特征尽量保持相似,而与其他类别的元素特征尽量产生差异,即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。

目前,较为主流的K-means聚类算法则为一种将欧氏距离作为基本特征度量的聚类方法,其分析流程如图1所示。

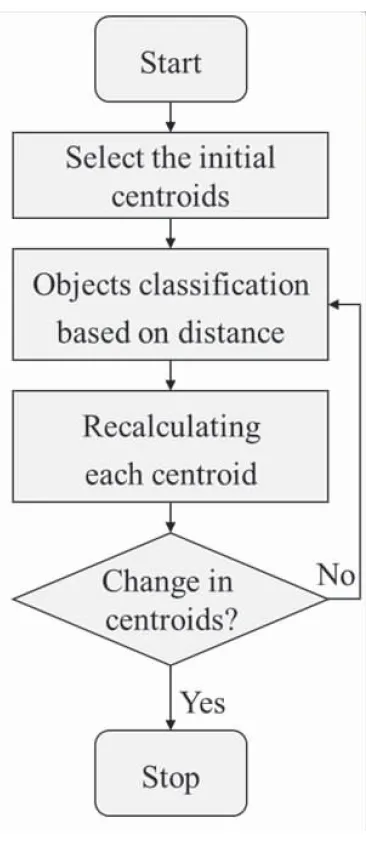
图1 K-means聚类算法框架Fig.1 Framework of K-means clustering algorithm

主要采用轮廓系数(Silhouette Cofficient,SC)来描述聚类结果的效果,轮廓系数描述了各样本点与类别内外距离的差异,其数值越大则代表各个样本与所在类别的中心点距离越近,说明聚类效果越好,反之则说明聚类效果越差。

K-means聚类算法优点在于其复杂度低,容易实施和理解,数据集较大时,其算法鲁棒性和分类效果较优;但其不足在于k值需要人工设置,初始聚类中心位置对分析结果有影响,局部异常值敏感性较高且对对非凸数据集效果不佳。为了避免初始聚类中心位置或k值对分析带来不良影响,本文中聚类分析均重复了5次至分析结果基本稳定,且多次改变k值。此外,本文数据集基于最优拉丁超立方抽样和高保真有限元分析得到,所以拟分析数据集不存在异常值,且在各结构参数维度上都近似为凸集,较为适合K-means聚类算法的应用。因此,本文采用K-means聚类算法面向高筋筒壳结构构型参数及承载特性开展聚类分析并总结具有高承载效率筒壳结构的参数分布特征。

2 常用加筋构型承载能力探究

作为一类新型加筋构型,高筋筒壳结构的承载潜力尚未被完全挖掘。因此,为探究高筋筒壳结构与传统低筋筒壳及蒙皮桁条结构的承载效率差异,本章以一个与CZ-5运载火箭燃料贮箱结构半径尺寸相当(直径5000 mm,高度4800 mm)的加筋筒壳为例,在相同材料体系、相同载荷条件前提下,面向三种不同的加筋构型(正置正交高筋筒壳、正置正交低筋筒壳、蒙皮桁条筒壳)开展结构参数优化,对比优化结果的承载能力,从而对比各加筋结构的承载效率。

本算例中,材料选用7050铝合金,弹性模量E为72 000 MPa,泊松比ν为0.3,密度ρ为2.82×10-6kg/mm3,屈服强度为455 MPa,强度极限为480 MPa,延伸率为12%。采用通用CAE软件Abaqus建立模型,单元选为四节点四边形线性减缩积分壳单元S4R。加筋筒壳下端面固定所有自由度,上端面的节点采用couple与中心处的参考点进行刚性耦合,并固定该参考点除轴向平动自由度外的其余五个自由度。经过网格收敛性研究,蒙皮处的单元尺寸选为30 mm,筋条高度方向划分2个单元。此外,经过加载速度收敛性研究,加载速度设置为100 mm/s。本文全部计算分析所采用的计算机配置具体如下:CPU,lntel(R) Xeon(R) Gold 6242R @3.10GHz;内存,256 GB/2933 MHz。单次几何非线性耗时约90 min,具体分析耗时会随单元与网格数量变化而上下波动。

采用通用优化软件Isight构建基于代理模型的优化框架,具体如图2所示。首先,在实验设计(Design of Experiment,DOE)阶段基于最优拉丁超立方抽样方法进行抽样,初始抽样规模为100个,并采用显式后屈曲分析获得结构承载能力。然后基于初始样本点数据建立径向基函数(Radial Basis Function,RBF)代理模型,并进一步基于代理模型采用多岛遗传优化方法进行寻优,岛数量与种群数量为10,进化代数为30代,其余参数均为Isight多岛遗传算法默认值。在优化结束后进行显式后屈曲分析,如果满足收敛条件则优化结束,否则将精细模型的计算结果加入至原样本点集中并重新建立代理模型,之后再次进入代理模型优化阶段,直至外层加点连续15代承载力无提升时,即认为满足外层的收敛性判断为止。

图2 基于代理模型的优化框架Fig.2 Framework of the surrogate-based optimization

优化列式如式(5)所示:

find:X=[ts,tr,numZ,numH,…]

Max:Fcritical

(5)

其中,优化目标为结构承载能力最大化,优化约束为结构质量Mass≤1500 kg,优化变量随着结构构型的不同而有所区别:(1)对于正置正交高/低筋筒壳,其优化变量具体包括蒙皮厚度ts、筋条高度hr、筋条厚度tr、纵筋数量numZ及环筋数量numH;(2)对于蒙皮桁条筒壳,其优化变量具体包括蒙皮厚度ts、外桁条数量numZ、中间框数量numH、外桁条厚度参数tup、tfuban及tdown、外桁条几何参数hall、hfuban及ldown、中间框厚度tzjk、中间框几何参数l1zjk、l2zjk及hzjk。几种加筋构型的构型参数具体如图3所示。

(a)Orthogonal cylindrical shell

(b)Skin-stringer cylindrical shell图3 加筋筒壳参数示意图Fig.3 Parameters of the stiffened shells

需要说明的是,由于旋压工艺加工外加筋结构更为合适,因此正置正交加筋筒壳均采用外加筋;蒙皮桁条结构中间框与外桁条采用Tie连接与主蒙皮耦合,设置容差为80 mm。

经过加点优化后,三种构型的优化迭代曲线均逐步趋于收敛,并最终得到优化解。优化迭代图如图4所示,设计变量上下限及得到的优化结果如表1所示。得到各构型的优化结果结构质量、承载能力和承载效率指标如表2所示。从表2可以发现,三种构型优化结果的结构质量均十分接近优化约束(1500 kg),说明所得到优化结果均已搜索到全局近似最优解。此外,在结构质量一致的情况下,正置正交高筋筒壳结构的承载能力显著优于低筋筒壳和蒙皮桁条筒壳结构,承载效率提升幅度为16.990%～54.741%。由于高筋筒壳结构放松了筋条高度的约束,导致筋条抗弯能力大幅提升,所以相对于传统构型产生了承载优势。优化结果说明高筋筒壳结构的承载潜力巨大,有望取代传统低筋构型成为新一代运载火箭主体结构选型。

图4 结构参数优化迭代路径Fig.4 Optimization iteration history of structural parameters

表1 设计变量上下限及优化结果Table 1 Lower and upper bounds and optimum values of design variables

表2 优化结果结构质量、承载能力及承载效率Table 2 Structural mass,collapse loads and load-carrying efficiency of optimized results

3 高筋筒壳承载规律探究

为了探究高筋筒壳结构的典型失效模式及承载规律,根据第二章高筋筒壳优化结果及DOE样本点,对典型高筋筒壳全加载过程的失效模式及承载规律进行讨论和分析。

最优结构的模型共包含75 816个单元和73 789个节点,其轴压位移-载荷曲线如图5所示。可以看出,高筋筒壳结构的主要失效过程:首先蒙皮在边界附近发生局部失稳;随后局部蒙皮与筋条进入塑性状态;然后纵向筋条发生局部失稳同时结构达到极限承载,进而伴随着筋条发生强度破坏;失稳波在筒壳表面快速扩散为整体波形,进而发生整体失效。其失效模式属于强度主导的局部弹塑性屈曲。

图5 最优正置正交高筋筒壳位移-载荷曲线(5倍变形放大)Fig.5 Axialload vs axialdisplacement curves of optimized cylindrical shell with high orthogonal ribs (deformation scale factor is 5)

为探究高筋筒壳的构型参数与结构承载效率的内在关系,本章基于聚类、相关性分析等数据分析方法,基于上章优化过程中的采点数据,挖掘结构参数与承载特征规律,进一步为工程人员提供设计指导。

首先面向上章中基于最优拉丁超立方抽样得到的100个初始采点数据开展分析。选择承载效率最高的10个结构(10个结构承载效率均高于24.0 kN/kg)。对其结构构型参数进行归一化处理,得到结果如图6所示。从图6可以发现,除了蒙皮厚度ts整体分布特征不明晰以外,其余高承载效率筒壳的结构参数均有较为明显的分布特征:筋条高度hr处于定义域中部,取值范围为37.6～67.0 mm;环筋数量numH较少而纵筋数量numZ较多,说明“疏环筋、密纵筋”是高承载效率筒壳结构的一项主要特征;筋条厚度tr处于定义域中上部,为6.2～11.8 mm;筋条厚度tr与蒙皮厚度ts的比值主要在1.8～4.0之间;筋条高度hr与蒙皮厚度ts的比值主要在10.1～24.0之间;所有结构的纵向筋条质量占全结构质量为50%～70%,说明纵向筋条为承力主体。

图6 高承载效率加筋筒壳结构参数归一化分布Fig.6 Normalized distribution of structural parameters of stiffened cylinder with high load-carrying efficiency

进一步基于K-means聚类算法对采样数据的结构质量与承载能力作为主要指标开展聚类分析,从而为后续分析提供具有高承载效率的结构构型数据集。基于K-means聚类算法开展无监督聚类分析,输入数据集为结构承载能力、结构质量及结构承载效率。分别设置类别数量k为2、3、4得到聚类结果如图7所示。

(a)Number of clusters k=2,SC factor=0.758 43

(b)Number of clusters k=3,SC factor=0.739 4

从图7可以发现,三种类别数量不同的聚类结果都主要按结构承载效率与质量对数据进行分类。且类别数量为2、3、4三种聚类结果得到的轮廓系数分别为0.764、0.738、0.690,轮廓系数随着类别数量的增加而逐渐降低,这说明过多的类别数量并不符合结构承载能力数据集合的分布规律。故在此采用类别数为2的聚类结果开展后续的统计分析。从图7(a)中可以发现,聚类结果主要按照结构质量及承载效率对结构进行分类,具体分为“高质量-高承载效率”(橙色)和“低质量-低承载效率”(蓝色)两类。而高承载效率即“轻质高承载”,是航天筒壳结构设计的主要目标。因此将对具有“高承载效率”特征的结构进行分析,从而剖析高承载效率的成因与机理。

首先基于Lilliefors检验对数据的承载效率指标进行正态分布检验,得到假设检验结果为h=0,符合正态分布,对应方差概率指标为0.4478,大于0.05,因此可以接受符合正态分布的原假设。进一步对高承载效率的结构构型参数-承载能力进行相关系数分析,得到结果如表3所示。

表3 结构承载效率与构型参数斯皮尔曼相关系数Table 3 Spearman correlation coefficient between structural load-carrying efficiency and configuration parameters

从表3中可以发现,除了承载效率与蒙皮厚度参数ts的显著性系数P值(0.114)大于接受阈值0.05,显著性不明显以外,其余构型参数与承载效率指标相关性分析的P值均小于0.05,可以认为自变量与因变量间存在显著的相关关系。其中,筋条厚度tr与筋条高度hr与承载效率的相关性系数分别为0.268与0.304,说明适当增加筋条高度与筋条厚度在一定程度上有利于加筋筒壳结构承载效率的提升,而纵筋数量numZ与环筋数量numH的相关性系数分别为0.744与-0.198,说明增加纵筋数量对提升结构承载效率作用最为明显,而增加环筋数量反而会降低结构的承载效率,因此应该选用“疏环筋、密纵筋”的加筋构型特征,这也与前述结论一致。

为了进一步验证不同半径高筋筒壳结构的承载规律,分别对直径为3350 mm,高度为3216 mm及直径为10 000 mm,高度为9600 mm的高筋筒壳结构开展承载规律分析,分析方法及分析流程与上文一致,得到结果如下:对于直径为3350 mm且承载效率较高的高筋筒壳结构而言,筋条高度hr取值范围为26.1～52.4 mm;筋条厚度tr取值范围为4.3～8.7 mm;筋条厚度tr与蒙皮厚度ts的比值主要在1.7～3.9之间;筋条高度hr与蒙皮厚度ts的比值主要在11.1～26.4之间。对于直径为10 000 mm且承载效率较高的高筋筒壳结构而言,筋条高度hr取值范围为88.7～144.2 mm;筋条厚度tr取值范围约为16.4～24.0 mm;筋条厚度tr与蒙皮厚度ts的比值主要在2.3～4.3之间;筋条高度hr与蒙皮厚度ts的比值主要在12.7～25.8之间。

通过不同直径高筋筒壳的横向对比可以发现,承载效率较高的高筋筒壳结构的构型参数存在以下分布特征:

(1)环筋分布较为稀疏,纵筋分布较密集,其中纵筋为承载主体;

(2)筒壳半径与筋条高度hr的比值主要在55.8～133.0之间,筋条高度hr与蒙皮厚度ts的比值主要在2.3～4.0之间;

(3)随着筒壳结构直径的增加,承载效率较高的结构中筋条的质量占比也不断增加。

4 结论

本文面向新型高筋筒壳结构承载潜力未知、承载规律不明的问题,通过加点优化、DOE分析、聚类分析及相关性分析等手段探究了高筋筒壳结构的承载潜力与承载规律,得出:

(1)相比于正交低筋、蒙皮桁条筒壳这两种传统构型,正交高筋筒壳结构承载效率存在显著优势,优化结果的提升幅度为16.990%～54.741%;

(2)具有高承载效率的高筋筒壳结构普遍呈现出“疏环筋、密纵筋”的构型特点,轴压下高筋筒壳结构承载主体为纵向筋条、蒙皮次之、环筋最末,增加纵向筋条数量对承载效率提升的作用最为显著;

(3)为提高高筋筒壳结构的承载效率,建议筒壳半径与筋条高度的比值在55.8～133.0之间,筋条高度与蒙皮厚度的比值在2.3～4.0之间,纵向筋条质量占全结构质量为50%～70%。

本文所关注的新型高筋筒壳结构及相关结论有望为未来重型运载火箭的主体结构设计提供参考。未来还需要结合高筋筒壳结构的构型特征与失效模式建立承载能力高效准确分析方法;考虑结构缺陷敏感性开展高筋筒壳结构抗缺陷设计,并开展轴压屈曲实验进一步验证高筋筒壳结构的承载优势。