球形封头开孔补强四种设计方法对比

孙 禹 华陆工程科技有限责任公司 西安 710065

压力容器的设计根据计算方法不同可以分为常规设计法和分析设计法。因为一般压力容器厚度方向尺寸远远小于另外两向尺寸，所以常规设计将压力容器简化为薄壳结构，以回转薄壳无力矩理论为基础，求得结构尺寸的解析解。经过多年的发展，常规设计理论已经日趋完善，目前工程领域中绝大多数压力容器均可以通过常规设计完成设计工作。近年来，随着计算机处理能力的不断提升，以有限单元法为理论基础的分析设计取得了很大的发展，在压力容器设计领域逐渐占有一席之地，尤其在常规设计无法解决的领域发挥了极大的作用，帮助设计人员完成设计工作，使得在复杂温度场、交变载荷等苛刻工况作用下的设备得以安全运行[1]。

壳体与接管相贯的结构在压力容器中最为常见，壳体开孔处的强度问题也直接影响设备的安全。常规设计对壳体的开孔补强主要采用等面积补强法；分析设计根据材料模型和结构响应不同可分为弹性分析和塑性分析，目前，国际上广泛应用的主要有应力分类法、极限载荷分析法、弹塑性应力分析法。本文分别使用上述方法对工程中的常见的球形封头及球形封头+接管结构进行计算，对比不同方法的设计裕量，以期对今后的设计工作提供帮助。

1 方法介绍

（1）等面积补强法主体思想即开孔挖去部分强度削弱，壳体和接管除去承受设计载荷以外的部分还会有多余的材料，削弱部分需要由接管及壳体多余部分面积来补充。

（2）应力分类法是将容器内产生的应力根据应力产生的内因进行分类。平衡载荷所需的应力为一次应力，满足变形协调所需的应力为二次应力或峰值应力。以等强度设计为原则，根据应力的危险性不同，对各应力设置不同的安全系数。应用等效线性化处理方法将应力分为薄膜应力、弯曲应力和峰值应力，再根据前述应力分类的方法判断应力类型，最后进行应力评定确定结构尺寸。我国目前暂用的分析设计标准JB 4732中使用的就是应力分类法[2]。

（3）极限载荷分析法认为，结构的高应力区达到材料屈服极限后，可由附近仍处于弹性区的材料帮助承载，当结构无法获得平衡解时，结构失效。极限载荷分析法的基本假设如下：

①材料应力-应变关系是理想弹塑性，即不考虑材料应变强化效应；

②采用小变形的应变-位移线性关系；

③满足基于变形前几何形状下的力平衡关系；

④满足Mises 屈服条件和关联流动法则。

在满足以上条件的前提下，采用数值分析技术进行计算，小的载荷增量再也不能获得平衡解时的载荷即为极限载荷。值得注意的是，根据极限载荷分析法所求得的解代表的位移和应变并无物理意义[3,4]。

（4）弹-塑性应力分析法的基本假设如下：

①采用材料的真实应力-应变曲线，即考虑材料应变强化或弱化效应；

②采用大变形的应变-位移非线性关系；

③满足基于变形后几何形状下的力平衡关系；

④满足Mises 屈服条件和关联流动法则。

在满足以上条件的前提下，采用数值分析技术进行计算，小的载荷增量再也不能获得平衡解时的载荷即为塑性垮塌载荷。该方法对材料的应变强化特性以及元件的变形所导致的应力重分布都在计算中直接计及，这与实际的结构行为比较接近。与极限载荷分析法和应力分类法相比，能较为精确地防止元件出现塑性垮塌失效[3,4]。

2 算例说明

本文旨在对比不同设计方法之间的特点，故不考虑材料强度随着厚度的增加而降低。文中计算所使用的材料许用应力均为189 MPa，屈服强度为345 MPa，抗拉强度为510 MPa，线弹性段的弹性模量为2.06×105MPa，泊松比为0.3。

ASME 标准规定极限载荷分析中理想弹塑性材料的屈服限应为设计应力强度的1.5 倍[5]，故本文计算模型中采用的理想弹塑性材料的理想屈服限为283.5 MPa，同时有限元程序中，使用KINH 选项定义材料服从von Mises 屈服准则、关联流动准则和等向强化准则，计算时关闭大变形选项，以满足小变形理论。

在进行弹塑性应力分析时，材料模型需要计及金属材料的应变强化特性，ASME 标准中给定了常用金属材料的应力-应变曲线模型，在已知材料屈服强度、抗拉强度、弹性模量的基础上，选择对应材料的参数值，使用该模型即可拟合出弹塑性分析所需的“真实”应力-应变曲线。此处的“真实”是相对于弹性材料和理想弹塑性材料而言，更接近金属材料实际本构关系的模型，并非实验获得的真实应力-应变曲线。使用前述参数拟合出弹塑性应力分析所使用的材料模型，见图1。将材料参数输入有限元软件中，同时定义材料服从von Mises 屈服准则和关联流动准则；计算时打开大变形选项，从而计及几何非线性的影响。

图1 弹塑性应力分析用应力-应变曲线

3 数值分析

以球形封头为例，球形封头内径为2000 mm，封头壁厚分别为10 mm，20 mm，60 mm，90 mm。分别使用解析法、应力分类法、极限载荷分析法和弹塑性应力分析法确定球形封头的最大允许载荷。

其中，极限载荷分析法和弹塑性应力分析法均是基于结构极限承载能力的方法，在设计合理的前提下，结构的极限承载能力均应大于结构所承受的载荷，所以，ASME 标准为节约计算成本，规定采用载荷-抗力系数法进行设计，即将设计载荷乘以安全系数作为输入的载荷值进行数值计算，如计算最终收敛，则所确定的结构是安全的，反之，则结构在设计载荷下不满足标准要求，需要调整结构尺寸重新进行计算。因为本文需要求得结构使用不同设计方法所确定的最大承载能力，所以采用塑性垮塌载荷法，即先使用较大的试探载荷，计算至不收敛，从而确定极限载荷，然后除以安全系数，从而确定结构可以承受的最大载荷值。

（1）解析法：根据式（1）可直接求得球形封头的最大允许载荷。

（2）应力分类法：建立有限元模型之后，施加试探载荷P0完成计算。然后沿封头壁厚方向做路径，提取薄膜应力值σ0，该应力为总体薄膜应力，根据标准规定应不大于材料许用应力。由于进行的是弹性计算，总体薄膜应力与载荷成正比，故可由式（2）计算得到封头的最大允许载荷。

（3）极限载荷分析法：建立有限元模型，施加试探载荷P0进行计算，直至计算不收敛为止。提取子步的时间值与P0相乘即为该子步对应的载荷值，最后计算收敛子步的载荷值即为结构的极限载荷，极限载荷除以安全系数1.5 即为最大允许载荷。

（4）弹塑性应力分析法：建立有限元模型，施加试探载荷P0进行计算，直至计算不收敛为止。提取子步的时间值与P0相乘即为该子步对应的载荷值，最后计算收敛子步的载荷值即为封头的垮塌载荷，垮塌载荷除以安全系数2.4 即为最大允许载荷。

按照上述方法分别计算四组球形封头算例的最大允许载荷值，结果见表1。P1、P2、P3、P4 分别代表解析法、应力分类法、极限载荷分析法和弹塑性应力分析法求得的最大允许载荷。

表1 球形封头最大允许载荷

为考察四种方法对于局部不连续结构的区别，在上述四组球形封头正中心开φ500 mm 的孔。为使接管补强作用和应力集中系数基本相当，每组算例接管壁厚、内外倒角尺寸与封头壁厚的比值均相同，各算例的结构尺寸见表2。

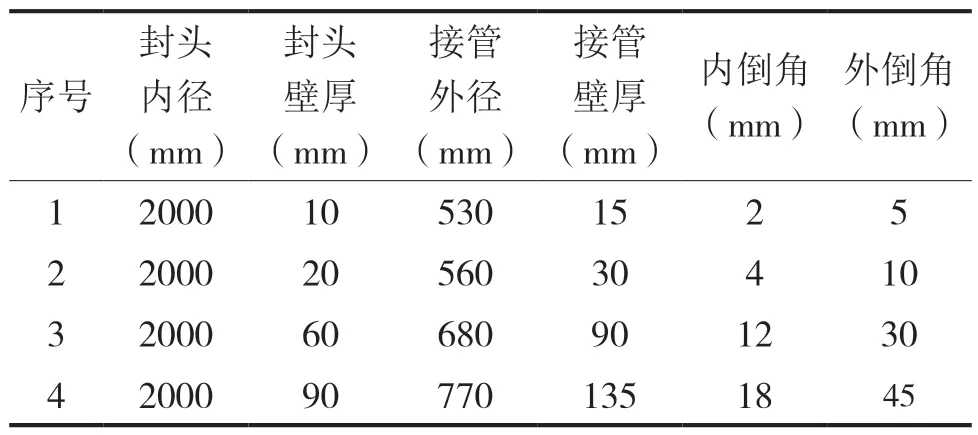
表2 球形封头+ 接管结构尺寸

对于球形封头+接管结构，无法直接获得最大允许载荷的解析解，本文通过试算的方法求得同时满足式（1）和等面积开孔补强法的最大允许载荷。

根据JB 4732 中表4-1 的典型情况应力分类方法，内压载荷在球壳接管附近引起的局部薄膜应力属于PL，引起的弯曲应力属于Q，本结构不承受交变载荷，所以无需考虑峰值应力F。使用应力分类法校核该结构的应力时，应同时满足SII=PL≤1.5KSm和SIV= PL+Q ≤3.0KSm。因为应力分类法的基本假设为弹性计算，故应力值与载荷为正比关系，所以将试探载荷值乘以许用应力和计算应力的比值可以直接反算出最大允许载荷，选择满足所有强度条件的最小载荷即为该结构的最大允许载荷，具体确定方法如下：

首先对结构施加试探载荷P0完成计算，然后选择多处路径进行应力线性化处理（路径示意见图2），确保获得最大局部薄膜应力σ1和最大局部薄膜加弯曲应力σ2，根据上述分析，最后可按式（3）求得最大允许载荷。

图2 路径示意图

分别计算球形封头+接管模型四组算例的最大允许载荷值，结果见表3。

表3 球形封头+ 接管模型的最大允许载荷

4 结果分析

在本文讨论的四种方法中，弹塑性应力分析法既考虑了材料非线性，又计及了几何非线性的影响，最能准确描绘结构的力学行为，求得的垮塌载荷最接近结构的极限承载能力。故以弹塑性应力分析法为基准，按式（4）计算另外三种方法求得最大允许载荷相对于弹塑性应力分析法求得载荷的相对误差。球形封头的最大允许载荷相对误差见表4，球形封头+接管模型的相对误差见表5。

表4 球形封头模型最大允许载荷相对误差百分比

表5 球形封头+ 接管模型最大允许载荷相对误差百分比

以壁厚与球壳半径之比t/R 为横坐标，以各方法求得最大允许载荷的相对误差为纵坐标绘图，其中，球形封头的计算结果见图3。

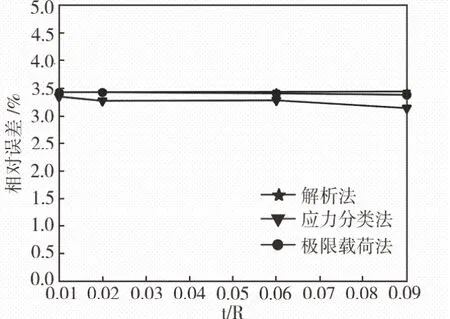
图3 球形封头模型相对误差

由图3 可知，对于总体连续的球壳而言，解析法、应力分类法和极限载荷法求得的极限载荷值基本一致，因为总体连续结构解析法和应力分类法均将总体薄膜应力限制在1 倍许用应力以内；极限载荷分析法认为总体应力达到屈服极限时结构失效，而屈服极限为1.5 倍的许用应力同时安全系数为1.5，所以，三种方法计算得到的极限载荷值非常接近。

在球壳模型中，解析法、应力分类法和极限载荷分析法计算所得最大允许载荷比弹塑性应力分析求得的最大允许载荷小3.5%左右，证明三种方法对于连续的薄壳结构而言都是偏于安全的。

球形封头+接管的计算结果见图4。

图4 球形封头+接管模型相对误差

由图4 可知，对于局部结构不连续的球形封头+接管模型而言，解析法、应力分类法和极限载荷分析法与弹塑性应力分析法的相对误差随着壳体厚径比增大逐渐减小，这说明随着壳体壁厚的增加三种方法设计裕量是逐渐减小的。

GB/T 150 的适用范围是≤35 MPa，当最大允许载荷由2.59 MPa 增加至32.55 MPa 时，均在标准适用范围内，解析法相对于弹塑性分析法的偏差由30.1887%减小至0.8227%。可见，在常规设计中，对于高温高压的厚壁容器应适当提高设计裕量，以避免设备在最大允许载荷附近服役的现象。

JB 4732 的适用范围是设计压力< 100 MPa的容器[6]。但是上述算例表明在最大允许载荷>22.18 MPa 时，应力分类法计算所得的承载能力已经大于弹塑性分析法，这说明仅从本文假定的算例来看，使用应力分类法设计是偏于危险的。

对于厚径比为0.09 的球壳+接管模型而言，解析法仅有0.8227%的裕量；应力分类法所允许的最大载荷大于弹塑性分析法确定的最大载荷，但是因为设计方法和材料性能均留有一定的安全系数，对比结构的垮塌载荷，以上两种方法均能保证结构安全服役，只是留有的设计裕量偏小。而对于同样尺寸的模型极限载荷法仍有7.5564%的裕量，说明当设备壁厚较厚时，可以考虑选择极限载荷法设计，从而在保证安全的前提下，有较为合适的设计裕量。

值得注意的是，上述进行的弹塑性分析仅能防止结构不发生垮塌失效，对于变形量限制较为严格的场合，应该提出适当的使用准则，从而防止结构在承载范围内因变形量过大而失效的情况发生。例如：成对法兰的泄露、塔器的挠度超标等。

5 结语

根据前述计算结果及论述，可得出以下结论：

（1）对于连续的薄壳结构，常规设计法、应力分类法、极限载荷分析法均能保证结构安全，且三种方法的计算结果基本一致。

（2）常规设计法以回转薄壳无力矩理论为基础，该方法的安全裕量随着厚径比的增大而逐渐减小，在使用常规设计法时，对于壁厚较大的设备应适当提高设计裕量。

（3）对于厚径比较大的设备而言，某些特定尺寸的结构使用应力分类法所留有的设计裕量可能偏小，此时宜考虑采用极限载荷分析法或者弹塑性分析法进行设计或者验证计算结果是否留有合适的设计裕量，以获得安全合理的结构。

（4）使用极限载荷法设计厚径比较大的设备时，有较为合理的设计裕量，且计算成本明显小于弹塑性分析法。