场地条件对高速铁路桥梁-轨道系统震后残余变形的影响

余建，周旺保,2，蒋丽忠,2，刘祥，冯玉林

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 中南大学 高速铁路建造技术国家工程研究中心，湖南 长沙，410075；3. 福建工程学院 土木工程学院，福建 福州，350118；4. 华东交通大学 土木建筑学院，江西 南昌，330013)

2008 年8 月1 日，中国开通了京津城际铁路，这是中国首条设计速度达到350 km/h的高速铁路。高速铁路具有安全性好、舒适性高以及耗时少等优点[1-3]，目前，中国的高速铁路建设快速发展，高铁网络在中国中部和东部地区开始了全面建设。截止2021年底，中国的高铁里程已达到4万km[4]。

目前，中国的高铁网络建设逐渐向西部地区拓展[5-6]。中国的西部地区地质条件复杂，断裂带分布密集，地震活动频繁。为了跨越复杂的地形，高速铁路往往建立在桥梁上，高铁桥梁累计全长可达到几百甚至上千公里。高铁桥梁途经地区的场地条件复杂，研究场地条件对高铁桥梁地震响应的影响将有利于高速铁路桥梁的设计、运营和维修。

场地条件对地震动的幅值和频谱特性均具有明显的影响作用，具体表现为对地震动幅值的放大和缩小，以及对地震反应谱形状的改变，场地条件能够直接影响建筑物破坏的严重程度。WOOD 在实地调查1906 年发生的美国旧金山大地震时发现，不同场地条件上的建筑物震害差异显著[7]。软弱地基上的建筑物损坏程度比坚硬地基上的严重，复杂场地的建筑物损坏程度比简单场地的严重；长周期结构在软弱地基上的震害较重，短周期结构在坚硬地基上的震害也较重。

世界各地的震害研究都与上述结论基本相同。胡聿贤等[8]在调查1970 年中国云南通海地震时发现，基岩地震动的幅值小，持续时间短；坚硬地基上的建筑物的震害轻，软弱地基上的建筑物震害严重。此外，胡聿贤等[8]在调查1975 年中国辽宁海城地震时发现软而厚的土层可以过滤地震动中的短周期成分，使长周期成分占据主导地位，进而导致长周期建筑物在地震中损伤严重。

为了区分不同的场地条件，各国把场地分类纳入到设计反应谱中。例如，中国的GB 50111—2006《铁路工程抗震设计规范》[9]按照土体剪切波速把场地依次分为I0 到Ⅳ类，美国的ASCE/SEI 7-05 规范[10]将场地土体由坚硬到软弱依次分为A到F共六类，每一类场地对应不同的设计反应谱形状，不同的设计反应谱将对应不同的结构响应。

这种方法能考虑场地条件对结构最大地震响应的影响，但无法考虑场地对结构残余地震响应的影响。因为反应谱法是一种弹性范围内的概念，不能用于分析结构的弹塑性变形，而结构的弹塑性变形是残余变形的主要来源。钢筋混凝土结构在经历强震作用后会产生一定的残余变形，残余变形是震后结构可修复能力的重要指标。高速铁路桥梁作为重要的交通基础设施以及生命线工程，需要保证其在强震作用下具有良好的可修复性。

因此有必要对不同场地条件下的高速铁路桥梁-轨道系统震后残余变形展开分析和比较。本文作者以带CRTS Ⅱ型板式无砟轨道结构的高速铁路多跨简支梁为研究对象，分析高速铁路桥梁-轨道系统的震后残余变形分布规律，提出一种描述震后残余变形的特征曲线，比较不同地震强度下场地条件对震后残余变形的影响，为震后高速铁路的设计、运营和维修提供参考依据。

1 有限元模型

本文采用的有限元模型包括：1) 基于ANSYS建立的高速铁路桥梁-轨道系统有限元模型，用于计算高速铁路桥梁-轨道系统的地震残余响应；2) 基于MATLAB软件建立的高速铁路桥梁-轨道-列车有限元模型，用于计算高速列车在震后轨道残余不平顺下的动力响应。

1.1 高速铁路桥梁-轨道系统

高速铁路桥梁-轨道系统(图1)由桥梁结构和轨道结构两部分组成。桥梁结构包括箱梁、支座、桥墩等结构。箱梁采用长度为32.5 m 的预应力混凝土箱梁，相邻主梁之间间隔0.1 m。桥墩采用圆端型实体桥墩，墩高范围为3～20 m，墩顶下方3 m以内的桥墩截面为渐变截面。当墩高小于等于14 m时，墩顶下方3 m外的桥墩截面相同；当墩高大于14 m 时，3 m 外为坡度1∶45 的渐变截面。每跨主梁底部设置有4 个支座，分别是1 个固定支座、2 个单向滑动支座以及1 个双向滑动支座；支座类型为盆式橡胶支座，4个支座的竖向极限承载力是5 000 kN，固定方向的水平极限承载力为1 000 kN，滑动方向的水平极限承载力是固定方向的10%。主梁和桥墩之间设置有防落梁装置，当墩梁相对位移达到20 cm时，防落梁装置开始发挥作用限制箱梁移动。

图1 高速铁路桥梁结构Fig. 1 Bridge structure of high-speed railway

轨道结构(图2)包括滑动层、底座板、摩擦板、端刺、CA砂浆层、轨道板、扣件、钢轨、剪力齿槽、剪切钢筋、侧向挡块等结构。滑动层由铺设在箱梁表面的土工布和塑料膜组成，滑动层可以实现底座板和箱梁之间的隔离，减小桥梁温度伸缩引起的轨道结构应力。滑动层的上方铺设有底座板，底座板是跨越梁缝的纵向连续钢筋混凝土结构；底座板的两端布置有摩擦板和倒T 型端刺，端刺的水平刚度很大，可以将轨道结构的列车制动力传入路基。底座板的上方铺设有砂浆层，砂浆层具有缓冲作用，能够减少轨道结构在列车荷载下的振动。砂浆层的上方是轨道板，轨道板的上方是扣件和钢轨，扣件的布置间隔是0.65 m，轨道板和钢轨都是纵向连续结构。在固定支座上方的箱梁和底座板之间设置有由凹槽和栓钉组成的剪力齿槽，剪力齿槽的纵向刚度很大，能够将列车制动力传递到桥墩上。在梁缝、端刺两侧的底座板和轨道板之间设置有剪切钢筋用以减小梁端转角引起局部不一致变形。底座板的两侧设置有侧向挡块用以限制底座板的横向、竖向移动以及轨道板的横向移动，侧向挡块的布置间距是6.5 m。

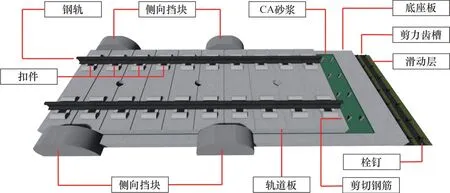
图2 高速铁路轨道结构Fig. 2 Track structure of high-speed railway

采用ANSYS 有限元模型建立高速铁路桥梁-轨道系统的有限元模型(以5跨简支梁为例，图3)。箱梁的截面刚度较大，在地震作用下基本保持弹性状态[11]，因此将箱梁模拟为弹性梁单元。根据文献[12]，高速铁路桥梁支座在地震作用下的力-位移曲线近似为理想弹塑性，因此将支座模拟为理想弹塑性弹簧单元。

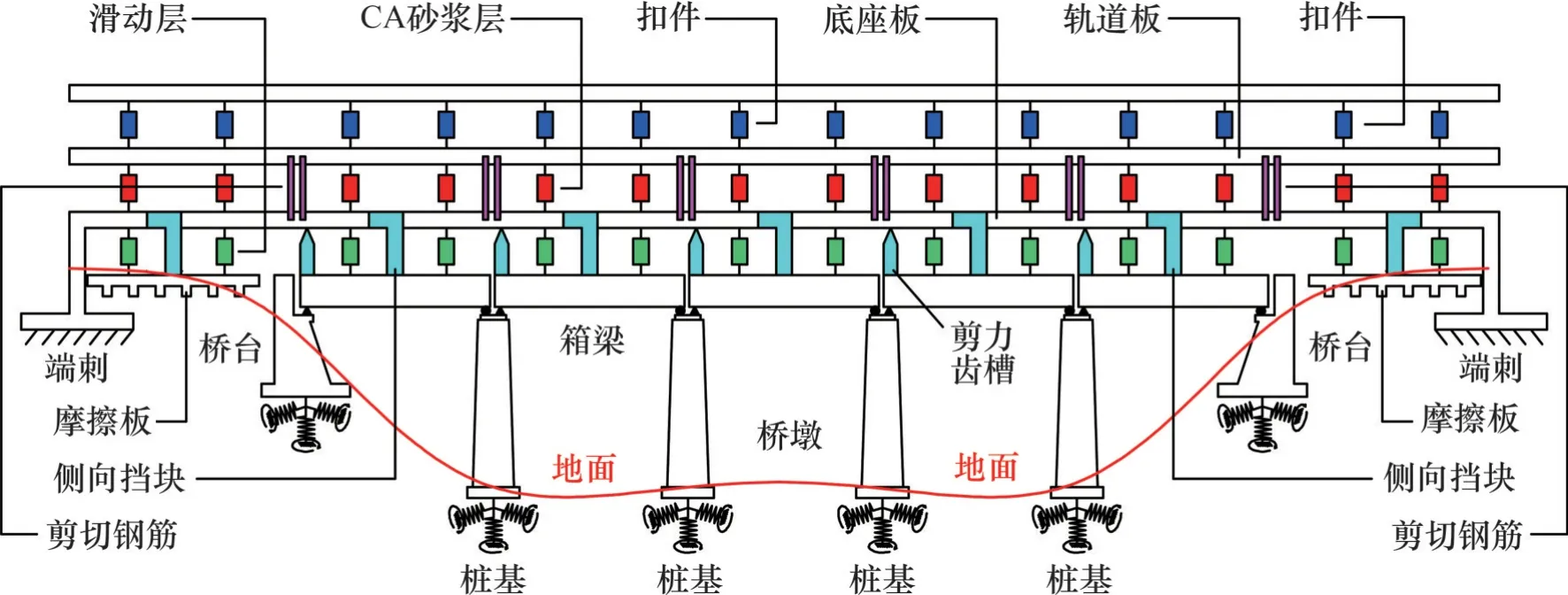
图3 高速铁路桥梁-轨道系统非线性三维耦合模型Fig. 3 Nonlinear three-dimensional coupling model of high-speed railway system

根据文献[11]，底座板、轨道板、钢轨、摩擦板在地震下不会发生明显损伤，因此将它们模拟为弹性梁单元。滑动层、CA砂浆层是纵向连续的层状结构，将它们等效为间隔0.65 m 的等间距理想弹塑性非线性弹簧单元，文献[13]给出了它们的力-位移曲线；将支座、端刺、防落梁装置、扣件、剪力齿槽、剪切钢筋、侧向挡块模拟为理想弹塑性非线性弹簧单元，文献[14-16]给出了它们的力-位移曲线。非线性弹簧单元的屈服力和屈服位移见表1，非线性弹簧单元的力-位移曲线见图4，弹性梁单元的材料参数和力学特性见表2。

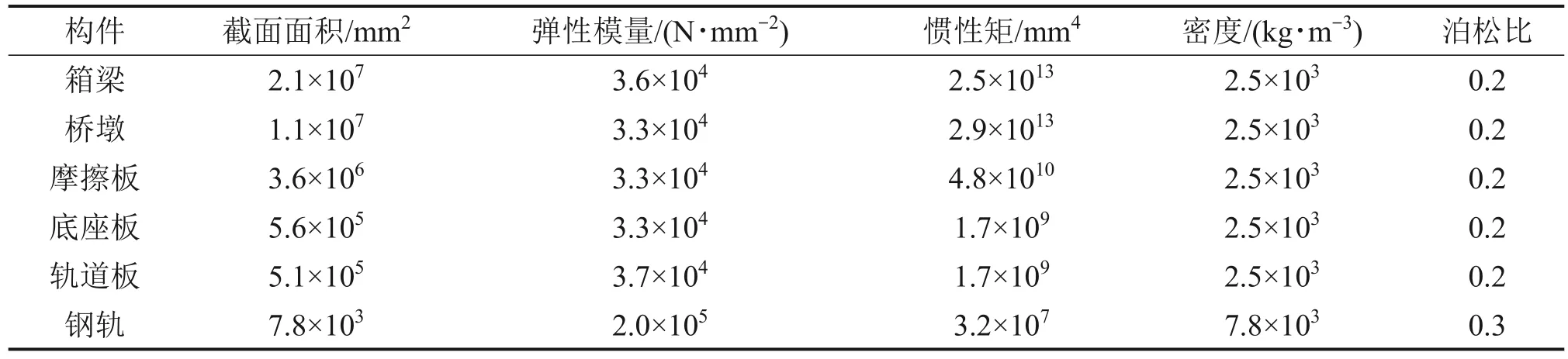
表2 结构的材料参数和力学特性Table 2 Material parameters and mechanical properties of structures

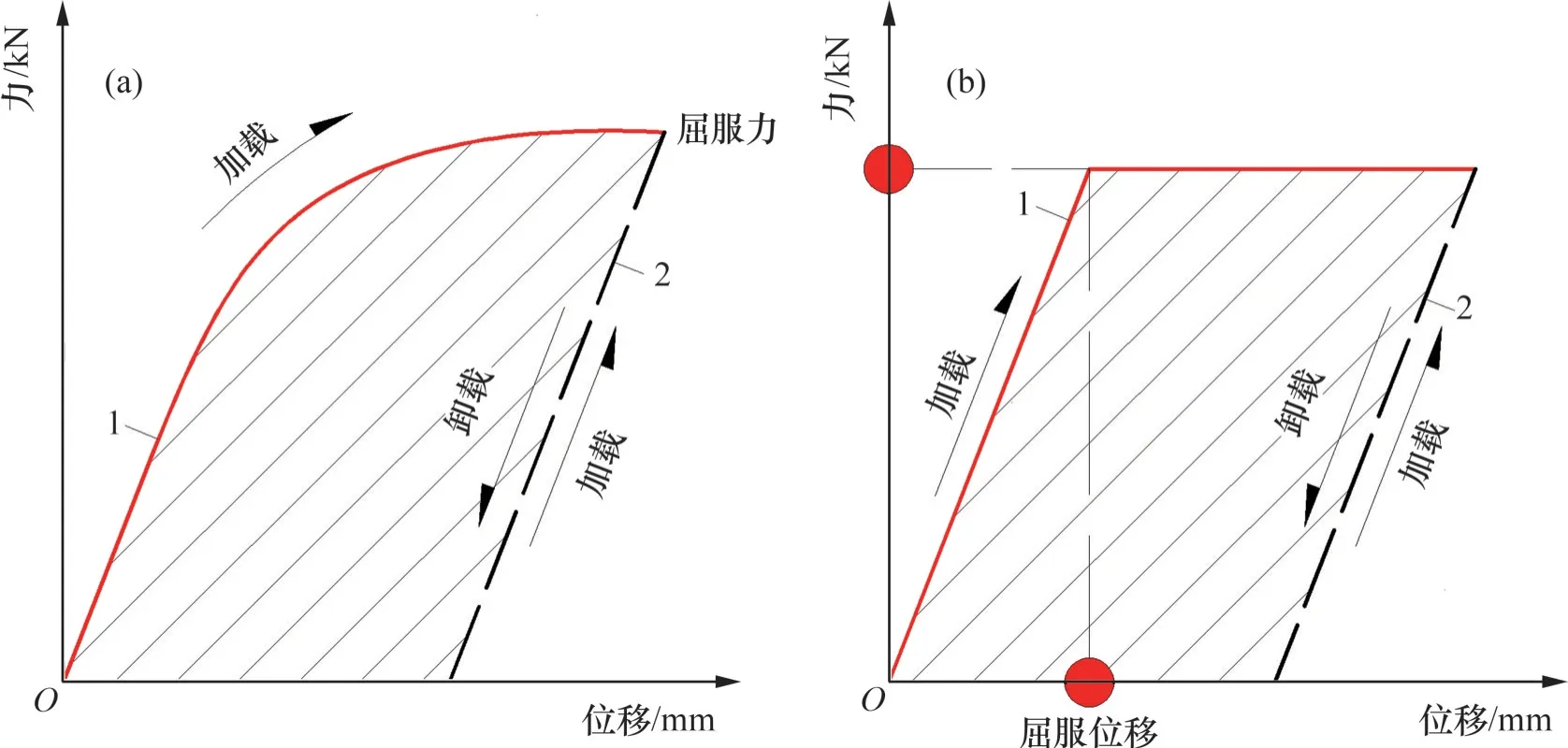
图4 非线性弹簧单元的力-位移曲线模型Fig. 4 Force-displacement curve model of nonlinear spring elements

桥墩在强震作用下会进入塑性状态，其非线性行为可以用弯矩-曲率曲线描述，文献[17]提供了高速铁路桥墩的弯矩-曲率曲线参数(图5)。广义梁单元能实现梁柱的弯矩-曲率定义，因此将桥墩模拟为广义梁单元。为了便于建模，箱梁和桥墩的单元长度都取0.65 m。此外，模型阻尼考虑为瑞丽阻尼，阻尼比取0.05。不考虑桩-土相互作用，模型的桥墩底部施加固定约束。迭代次数、收敛准则等按软件默认设置。

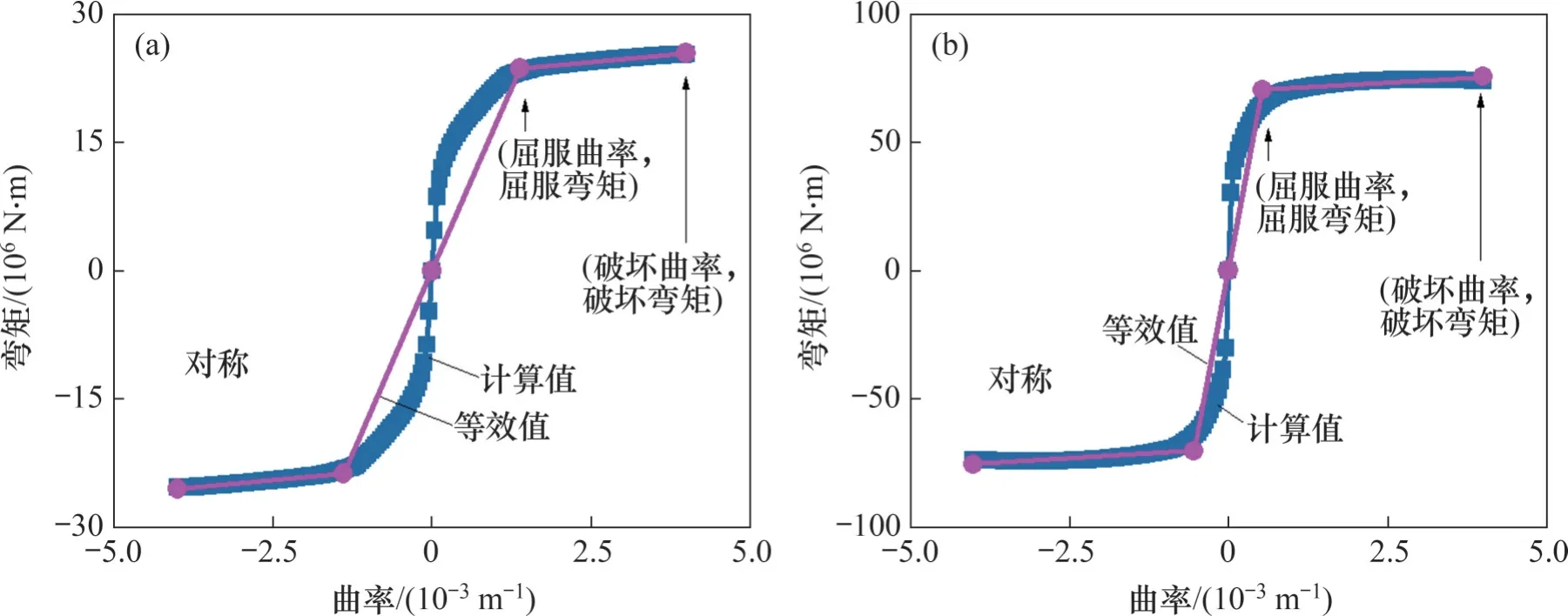
图5 桥墩弯矩-曲率曲线Fig. 5 Moment curvature curve of pier

1.2 高速铁路桥梁-轨道-列车系统

高速铁路桥梁-轨道-列车系统模型由列车模型、轨道模型和桥梁模型3个部分组成。列车模型由8 节车厢组成，每节车厢包括1 个车体、2 个转向架以及8个轮对。每个车体有yv，zv，φvx，φvy和φvz5 个自由度；每个转向架有yb，zb，φbx，φby和φbz5 个自由度；每个轮对有yw，zw，φwx和φwz4 个自由度；每节车厢一共具有31个自由度(图6)。各个符号下标中的v，b 和w 分别表示车体、转向架和轮对；x，y和z分别表示纵向、横向和竖向。

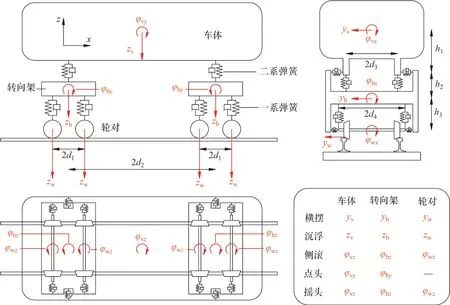
图6 高速铁路桥梁-轨道-列车系统线性三维耦合模型Fig. 6 Linear three-dimensional coupling model of high-speed railway bridge-track-train system

图6展示了列车模型的参数，其中d1表示同一转向架两轮对的半间距，d2表示前后转向架的半间距，d3表示二系悬挂的横向半间距，d4表示一系悬挂的横向半间距；h1表示车体重心与二系悬挂的距离，h2表示二系悬挂与转向架的距离，h3表示转向架与一系悬挂的距离；k和c分别表示弹簧的刚度和阻尼，下标的p 和s 分别表示一系和二系悬挂。参数的取值见表3[18-19]，表3中的m和I分别表示质量和惯性矩。

表3 列车模型参数Table 3 Parameters of train model

轮轨接触考虑为刀口接触[20]，即轮对踏面考虑为理想圆锥形，钢轨考虑为一铰点；轮轨之间的横向游隙设为10 mm，轮轨横向接触刚度取为1.6×107N/m。轮轨接触将产生法向力和蠕变力，采用赫兹接触理论[21]计算轮轨法向力，采用Kalker线性蠕变力模型[22]和Shen-Hedrick-Euristic非线性蠕变力模型[23]分别进行轮轨蠕变力的计算和校正。

此模型主要用于计算列车在震后轨道残余不平顺作用下的动力响应，因此对轨道模型和桥梁模型进行了简化。箱梁、底座板、轨道板、钢轨、桥墩模拟为弹性梁单元，梁单元的材料和截面特性见表2；支座、滑动层、CA 砂浆层扣件等效为间隔0.65 m的线性弹簧单元，弹簧单元的水平向线性刚度与表1 中的相同，竖向刚度取2.0×109N/m。模型中不考虑路基、摩擦板、端刺、侧向挡块、剪力齿槽和剪切钢筋等结构。详细的动力学方程以及矩阵拼装过程见文献[24-25]。

2 地震动输入

中国的《铁路工程抗震设计规范》[9]提供了在各种情况(不同的地震强度和震中距)下四类场地(I、Ⅱ、Ⅲ和Ⅳ类)的设计反应谱曲线。其中，I、Ⅱ、Ⅲ和Ⅳ类场地对应的土层类型分别为岩石、碎石、细砂和淤泥，对应的土层剪切波速vs范围分别为vs≥500 m/s， 500 m/s＞vs≥250 m/s， 250 m/s＞vs≥150 m/s，vs≤150 m/s。这有利于直接比较场地条件对于结构震后残余响应的影响，因此，本文采用设计反应谱来生成地震加速度时程。

《铁路工程抗震设计规范》[9]指出，9 度区地震活动频繁，该地区的工程结构需进行特殊设计。本文采用的高速铁路桥梁结构尺寸适用于8度区及以下地区，因此本文取8度区作为研究对象，地震的超越概率分别取为63%、10%和2%。高速铁路桥梁并非长周期结构，因此，本文不考虑中、远场地震的影响，震中距分组取为1组。结合上述参数，计算四类场地的设计反应谱(图7)。从图7 可以看到：场地的土层类型对于反应谱的形状有明显影响，土层越松软，反应谱曲线的平台段越长，这表明松软的土层可以放大地震动中的长周期成分，加剧结构的地震损伤。

图7 不同地震强度下四类场地的设计反应谱Fig. 7 Design response spectra of four sites under different earthquake intensities

通过自编的MATLAB 人工地震波计算程序，生成对应于图7(b)～(d)中各场地反应谱的人工地震波各100 条，共计1 200 条地震波(100×12=1 200)，其中一条人工地震波(场地类别为I类，超越概率为2%)的加速度时程以及反应谱如图8 所示。在每条地震波的尾部增加一段时长为10 s的零值段以模拟结构在地震后的自由振动过程。高速铁路桥梁-轨道系统有限元模型的墩高取14 m，简支梁的跨数取9。将调整过后的1 200 条地震动作为激励，对有限元模型开展非线性时程分析，提取最后一个荷载步的结构响应作为震后残余响应。

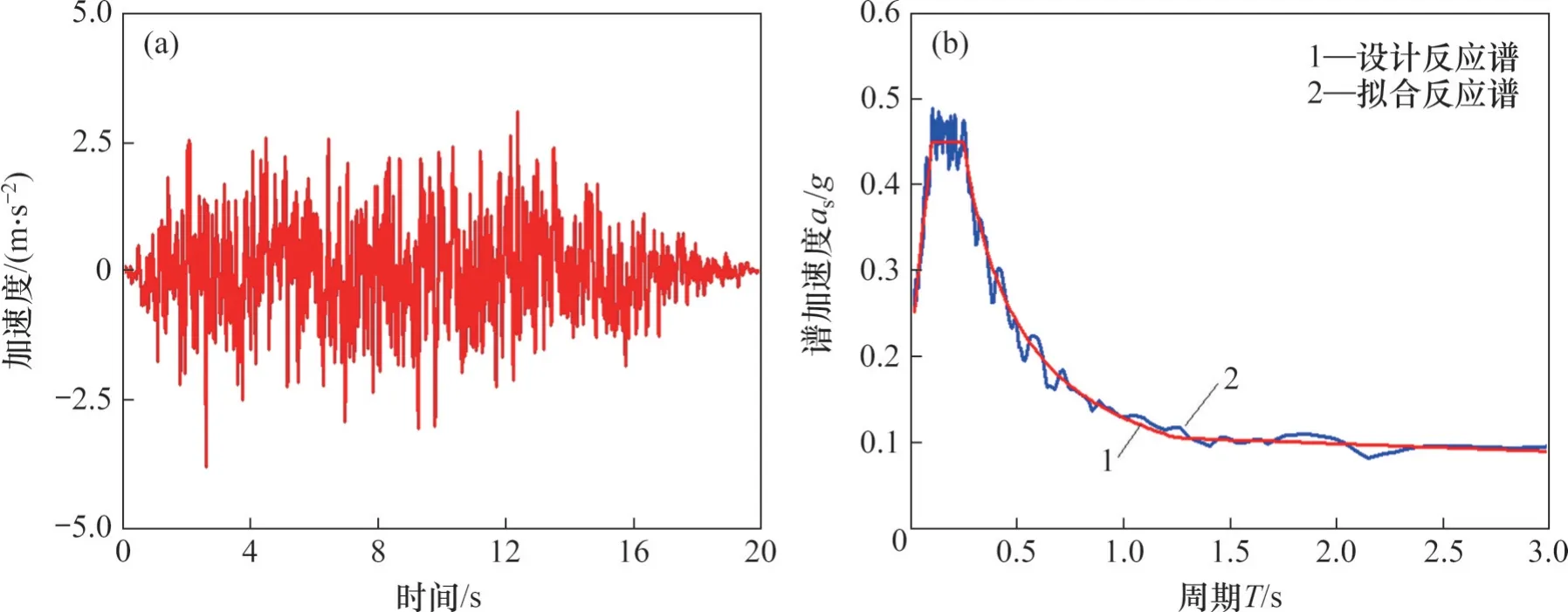
图8 罕遇地震下I类场地的人工地震动及其反应谱Fig. 8 Artificial ground motion and its response spectrum of site I under rare earthquakes

3 震后残余变形分布

研究高速铁路桥梁-轨道系统的震后残余变形分布是震后维修和运营的基础[26-28]。从I类场地的100 条地震动(罕遇地震)中随机选取2 条(图9)作为有限元模型的加速度激励，激励方向分别为横向和纵向，计算高速铁路桥梁-轨道系统的震后残余响应，残余响应的最大值见表4。

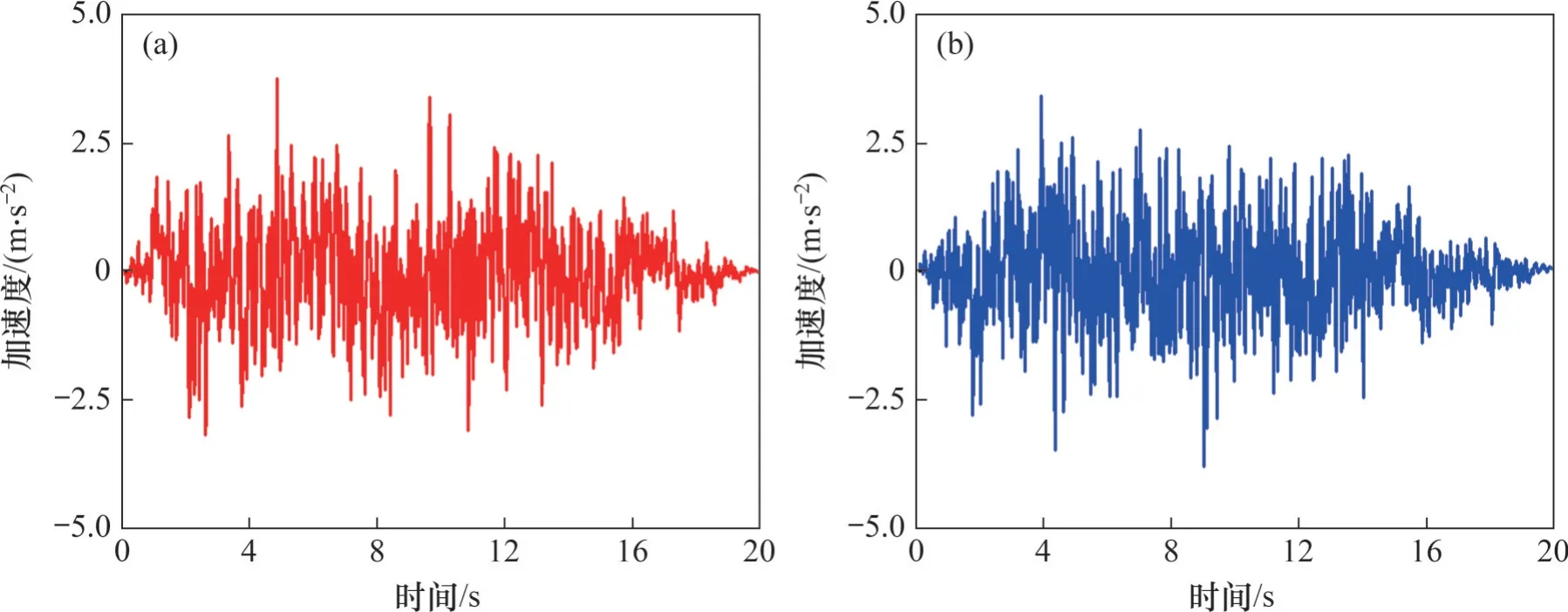
图9 随机抽取的2条人工地震动Fig. 9 Two randomly selected artificial ground motions

表4 高速铁路轨道桥梁-轨道系统最大地震残余响应Table 4 Maximum seismic residual response of high-speed railway bridge-track system

在横向地震作用下，支座的横向残余变形达到了25.77 mm(屈服变形2 mm)，这表明支座在震后发生了严重的横向变形，箱梁发生了明显横向位移；桥墩最大残余弯矩为9.29 MN·m(屈服弯矩约为75 MN·m)，这表明箱梁的横向位移引起了桥墩的偏心弯矩。端刺、剪力齿槽、侧向挡块的震后残余变形为0 mm，归其原因为这些结构的强度相对较大，在地震中没有发生损伤。滑动层、CA砂浆层、扣件、剪切钢筋的残余剪切变形为0，归其原因为连续布置的大刚度侧向挡块减少了底座板、轨道板之间的横向相对位移。

将箱梁、底座板、轨道板和钢轨节点的横向残余位移以及支座的横向残余变形同时绘制在图10 中，图10 的坐标零点对应于第一跨箱梁的起始点，红点之间的纵向间隔为32.6 m(箱梁长度32.5 m，加上0.1 m的箱梁间隙)，可以看到靠近两侧的节点位移和支座变形基本为0，中部的数值逐渐增大，这是由于底座板的两端布置有端刺，端刺锚固在路基之中，路基通过端刺和底座板对桥梁结构的横向运动施加了约束效应，这种约束效应随着桥梁里程增大而减小。

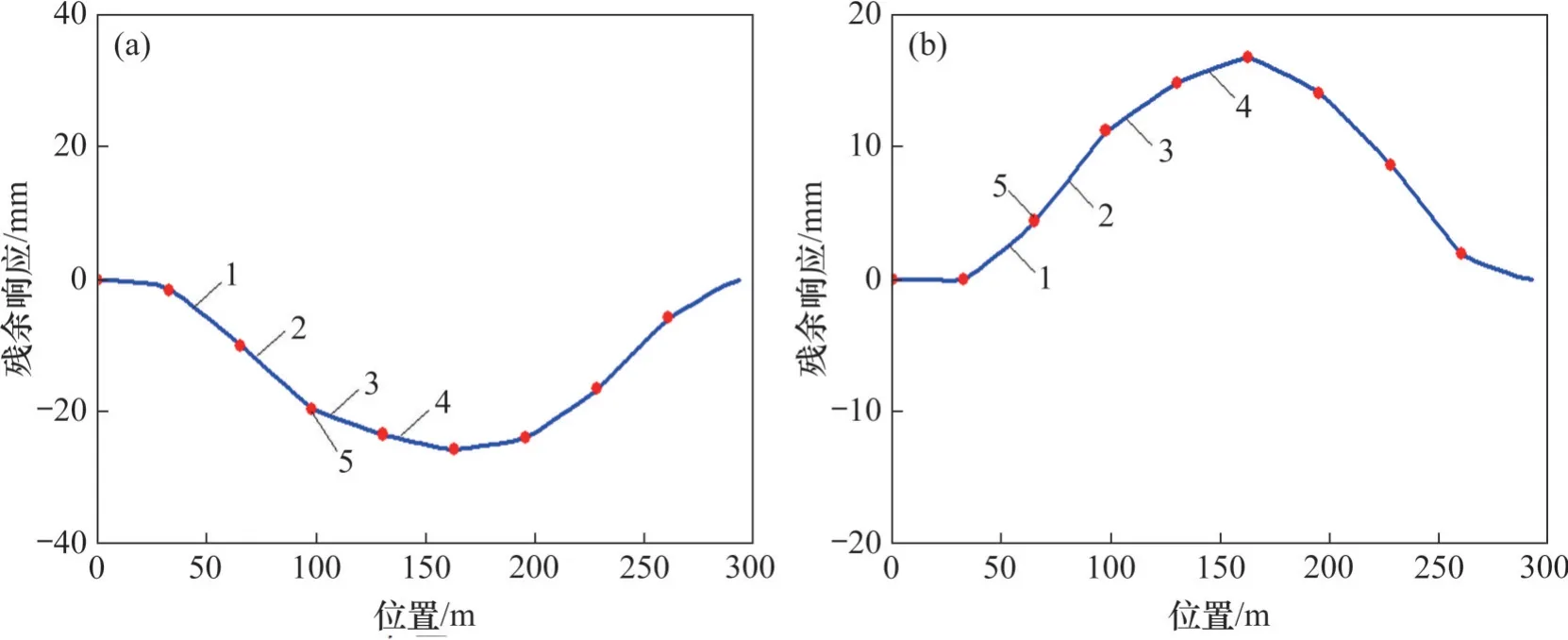
图10 不同地震波的横向残余响应Fig. 10 Transverse residual response of different seismic waves

箱梁、底座板、轨道板和钢轨节点的横向位移曲线基本重合，这表明箱梁、底座板、轨道板和钢轨彼此之间没有明显的残余相对位移；箱梁、底座板、轨道板和钢板的节点位移与支座变形基本相同，这表明横向地震后支座变形是高速铁路桥梁-轨道系统残余变形的主要来源，桥梁-轨道系统的震后维修应主要以支座更换以及箱梁、轨道复位为主。

在纵向地震作用下，各个构件的残余响应基本为0，归其原因为路基通过端刺和底座板对桥梁结构的纵向运动产生了显著的约束效应，因此，本文主要以横向地震作用下的高速铁路桥梁-轨道系统的震后残余变形作为研究对象。

4 震后钢轨残余位移的特征曲线

第3节的研究结果表明，箱梁、底座板、轨道板和钢轨节点的横向位移曲线基本重合，因此，震后钢轨残余位移曲线可以用来描述高速铁路桥梁-轨道系统的震后残余变形分布。基于震后钢轨残余位移的行车速度预测是高速铁路桥梁-轨道系统残余地震响应研究的重要组成部分[29-30]，然而从图10 可以看到，不同地震动作用后钢轨残余位移曲线的形状和幅值差异很大，这给震后行车速度阈值的确定带来困难。本节将基于短时傅里叶变换和假设检验原理，利用随机的震后钢轨残余位移曲线集合，构造一种确定的钢轨残余位移特征曲线，为震后行车模拟提供不平顺输入。

4.1 构造方法

若将震后钢轨残余位移曲线视为随机信号，则这种随机信号具有明显的非平稳特性。根据信号的统计特征是否随时间变化，信号可以分为平稳随机信号和非平稳随机信号。平稳信号的特征分析往往基于傅里叶变换，而非平稳信号的特征分析则需要依靠短时傅里叶变换、小波变换或者S变换等方法。其中，短时傅里叶变换因操作流程简单，物理意义明确，已在工程领域得到了广泛应用。

4.2 实例分析

以I类场地为例，地震的超越概率取2%，计算100条地震作用后的钢轨残余位移曲线Yi(图11(a))。将这些曲线作为样本，高速铁路桥梁-轨道系统震后钢轨残余位移特征曲线的构造步骤如下。

图11 震后钢轨残余位移特征曲线构造步骤Fig. 11 Construction steps of characteristic curve for rail residual displacement after earthquakes

1) 为了防止信号丢失，在钢轨残余位移曲线的两端分别增加长度为50 m的零值段。以图10(a)中的钢轨残余位移为例，图11(b)所示为加长后的钢轨残余位移。

2) 根据式(1)～(4)，不平顺数据点的采样间隔ΔL取0.25 m，空间采样频率为4，窗函数长度取51，计算100组钢轨残余位移曲线的演变功率谱密度。图11(c)所示为图11(b)中钢轨残余位移曲线的演变功率谱密度。

3) 根据式(5)～(9)，显著水平α取0.05，测试gi散点的正态性，测试结果见图11(d)。从图11(d)可以看到：在不同频率-空间坐标上100 个gi散点的J2计算值均为0，表明gi散点服从对数正态分布。

4) 根据式(10)～(13)，显著水平β取0.05，计算gi(f，x)的上界曲面gu(f，x)(图11(e))以及演变功率谱密度上界Gu(f，x)(图11(f))。可以看到，在频率区间0.01～0.1 m-1，演变功率谱密度的幅值较大；在大于0.1 m-1的频率范围内谱密度基本接近于0。这表明钢轨残余位移曲线以低频成分为主，其原因为连续布置的侧向挡块能够阻止轨道结构发生过大的局部变形，底座板、轨道板和钢轨在地震作用后没有明显的弯折现象[32-33]。

5) 根据式(14)～(16)，构造对应于Gu(f，x)的钢轨残余位移Yu(图11(g))，将其作为震后钢轨残余位移的特征曲线。

6) 基于2.2节的高速铁路桥梁-轨道-列车模型，将图11(a)中的Yi(i=1，…，100)和图11(g)中的Yu分别作为不平顺激励，列车的速度取为350 km/h，分别计算列车在Yi和Yu激励下的车体横向加速度ai和au(图11(h))。从图11(h)可以看到：au大于所有的ai散点，其原因为Gu是任意频率-空间坐标(f，x)上的演变功率谱密度上界，Gu对应的特征曲线能够激发更剧烈的列车振动，这表明了特征曲线构造方法的合理性。

5 场地条件对震后残余变形的影响

第3 节的研究表明，高速铁路桥梁-轨道系统震后残余变形的分布模式表现为支座变形以及由此引起的上部结构偏移，而第4节中用震后钢轨残余位移的特征曲线表示桥梁-轨道系统的残余响应。因此，本节将以震后支座残余变形和钢轨残余位移特征曲线为研究对象，分析场地条件对高速铁路桥梁-轨道系统震后残余变形的影响。

5.1 支座残余变形

将第2 节的1 200 条加速度时程作为激励，计算不同地震强度和不同场地条件下的支座残余变形(图12～15)。比较不同地震强度下的残余变形可以看到，在多遇地震作用下，支座残余变形基本为0；随着地震强度增大，支座残余变形迅速增大。归其原因为当地震动强度较小时，支座处于弹性状态，地震结束后箱梁可以自行复位；当地震动强度较大时，支座进入屈服状态，支座内力到达极限，支座损伤急剧增加。因此，在多遇地震作用下，高速铁路桥梁-轨道系统无需维修；在设计地震或罕遇地震作用下，支座受损严重，支座残余变形显著，需要展开维修。

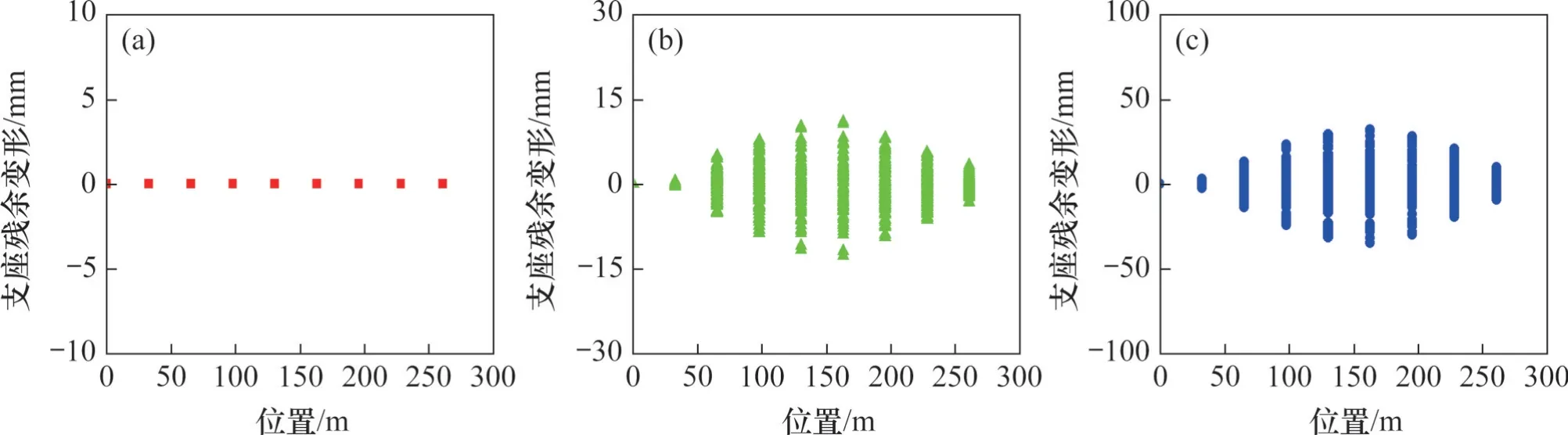
图12 不同地震强度条件下的支座残余变形(I类场地)Fig. 12 Residual deformation of bearing under different earthquake intensity conditions (site I)

图13 不同地震强度条件下的支座残余变形(Ⅱ类场地)Fig. 13 Residual deformation of bearing under different earthquake intensity conditions (site Ⅱ)

图14 不同地震强度条件下的支座残余变形(Ⅲ类场地)Fig. 14 Residual deformation of bearing under different earthquake intensity conditions (site Ⅲ)

图15 不同地震强度条件下的支座残余变形(Ⅳ类场地)Fig. 15 Residual deformation of bearing under different earthquake intensity conditions (site Ⅳ)

比较不同场地条件下的残余变形可以看到，随着场地类别的改变，支座残余变形明显增加，这表明随着土体柔软程度提升，支座残余变形增大。归其原因为柔软的土层可以在保留地震动短周期成分的基础上对长周期成分进行放大，柔软土层上的高速铁路桥梁-轨道系统响应更剧烈，导致更严重的支座损伤。

5.2 震后钢轨残余位移特征曲线

结合第4.2节的案例分析，计算不同地震强度和不同场地条件下的钢轨残余位移特征曲线(图16)。在多遇地震作用下，特征曲线的幅值基本为0；随着地震强度增大，特征曲线幅值的增长速度呈现出先慢后快的趋势。因此，在多遇地震作用下，震后高速列车运行无需减速；当地震强度大于多遇地震强度时，高速列车运行需要适当减速，减速程度应随地震强度增大而提高。随着场地类别的改变，特征曲线的幅值明显增加，这表明随着土体柔软程度提升，钢轨的震后横向偏移幅值增大。因此，在地震作用后高速列车由坚硬场地行驶至柔软场地时，需要适当减速。

图16 不同地震强度和不同场地条件下的钢轨残余位移特征曲线Fig. 16 Characteristic curves of rail residual displacement at different sites under different earthquake intensity conditions

6 结论

1) 在横向地震作用下，支座发生了严重的横向变形，箱梁发生了明显横向位移，端刺、剪力齿槽、侧向挡块的震后残余变形为0，滑动层、CA砂浆层、扣件、剪切钢筋的残余剪切变形为0。

2) 在横向地震作用下，箱梁、底座板、轨道板和钢轨彼此之间没有明显的残余相对位移，横向地震后支座变形是高速铁路桥梁-轨道系统残余变形的主要来源，桥梁-轨道系统的震后维修应主要以支座更换以及箱梁、轨道复位为主。在纵向地震作用后，各个构件的残余响应基本为0。

3) 在多遇地震作用下，支座残余变形基本为0；随着地震强度增大，支座残余变形迅速增大。在多遇地震作用下，高速铁路桥梁-轨道系统无需维修；在设计地震或罕遇地震作用下，支座受损严重，支座残余变形显著，需要展开维修。

4) 在多遇地震作用下，特征曲线的幅值基本为0；随着地震强度增大，特征曲线幅值的增长速度呈现出先慢后快的趋势。在多遇地震作用下，震后高速列车运行无需减速；当地震强度大于多遇地震强度时，高速列车运行需要适当减速，减速程度应随地震强度增大而提高。

5) 随着场地类别的改变，支座残余变形和特征曲线的幅值明显增加，在地震作用后高速列车由坚硬场地行驶至柔软场地时，需要适当减速。