A joint image compression and encryption scheme based on a novel coupled map lattice system and DNA operations∗#

Yuanyuan LI ,Xiaoqing YOU ,Jianquan LU ,Jungang LOU

1Department of Applied Mathematics,College of Science,Nanjing Forestry University,Nanjing 210037,China

2School of Cyber Science and Engineering,Southeast University,Nanjing 210096,China

3Department of Systems Science,School of Mathematics,Southeast University,Nanjing 210096,China

4Yangtze Delta Region (Huzhou) Institute of Intelligent Transportation,Huzhou University,Huzhou 313000,China

5School of Computer Science and Technology,Zhejiang Normal University,Jinhua 321004,China

Abstract: In this paper,an efficient image encryption scheme based on a novel mixed linear–nonlinear coupled map lattice (NMLNCML) system and DNA operations is presented.The proposed NMLNCML system strengthens the chaotic characteristics of the system,and is applicable for image encryption.The main advantages of the proposed method are embodied in its extensive key space;high sensitivity to secret keys;great resistance to chosenplaintext attack,statistical attack,and differential attack;and good robustness to noise and data loss.Our image cryptosystem adopts the architecture of scrambling,compression,and diffusion.First,a plain image is transformed to a sparsity coefficient matrix by discrete wavelet transform,and plaintext-related Arnold scrambling is performed on the coefficient matrix.Then,semi-tensor product (STP) compressive sensing is employed to compress and encrypt the coefficient matrix.Finally,the compressed coefficient matrix is diffused by DNA random encoding,DNA addition,and bit XOR operation.The NMLNCML system is applied to generate chaotic elements in the STP measurement matrix of compressive sensing and the pseudo-random sequence in DNA operations.An SHA-384 function is used to produce plaintext secret keys and thus makes the proposed encryption algorithm highly sensitive to the original image.Simulation results and performance analyses verify the security and effectiveness of our scheme.

Key words: Compressive sensing;Coupled map lattice (CML);DNA operations;Semi-tensor product

1 Introduction

Compressive sensing(CS)can compress and encrypt images simultaneously,so it is very suitable for digital image encryption(Rani et al.,2018;Testa et al.,2020;Chai et al.,2022b).CS uses a measurement matrix to compress high-dimensional sparse or compressible signals.The number of samples can be far less than the number of samples restricted by Nyquist’s sampling theorem,while the original signal can still be reconstructed from fewer samples(Donoho,2006).The compression sampling process can be considered as an encryption process,and the measurement matrix as a secret key has been proved to have sufficient computational security(Sreedhanya and Soman,2012;Fira,2015) to resist violent attacks (Wu CW et al.,2020).Some recent studies that investigated image encryption based on CS can be found in Zhou et al.(2021)and Chai et al.(2022a).However,the realization of CS on image encryption still faces the following three challenges:(1) An extremely large measurement matrix is still needed when encrypting large images,and it will waste a lot of bandwidth resources if all the elements of the measurement matrix are transmitted as secret keys;(2)CS is essentially a linear measurement process,so it cannot resist known-plaintext attacks(NPAs)or chosen-plaintext attacks(CPAs);(3)The CS reconstruction process is complicated and generally takes a long time.

For the first challenge,a classic solution is to combine chaotic cryptography with CS (Kafedziski and Stojanovski,2011;Li LX et al.,2020).The security measurement matrix is generated by a chaotic system.As long as the encrypter and decrypter negotiate the structure of the chaotic system,and the initial values of the chaotic system can be transmitted as secret keys,the time-consuming problem of transmitting each element of the measurement matrix can be solved(Shao et al.,2019).Therefore,the randomness of the chaotic system has a vital impact on the performance of an encryption system.

Impulsive coupled networks also have some applications in digital image processing technology(Li XD et al.,2019,2020).Research has shown that the information communication with a spatiotemporal chaotic system based on a coupled map lattice (CML) is more secure than that with a single map (Kaneko,1993;Wang Y et al.,2011;Wang XY and Wang,2012;Zhong and Xu,2015),because of its larger parameter space,better randomness,more chaotic sequences,and wider range of choices about the initial conditions (Zhang YQ and Wang,2014;Zhong and Xu,2015;Xu et al.,2016;Guo et al.,2018).Therefore,a CML system is applicable for secret key design in data protection,but the periodic windows in the bifurcation diagram of the CML system are still large and the spatial ergodicity of the randomness of time series is reduced.In addition,the small range of logistic map parameters restricts encryption schemes.Zhang YQ and Wang (2014)proposed a mixed linear–nonlinear coupled map lattice(MLNCML) system and obtained a larger range of parameters for chaotic behaviors,higher percentage of lattices in chaotic behaviors for most parameters,and fewer periodic windows in bifurcation diagrams for image encryption.

However,the range of logistic map parameters in MLNCML is not large enough,and the randomness of MLNCML is unstable.Therefore,we propose a novel mixed linear–nonlinear coupled map lattice (NMLNCML) system for our image encryption scheme,which further increases the range of logistic map parameters,improves the stability of chaotic features in Kolmogorov–Sinai entropy,and reduces the number of periodic windows in bifurcation diagrams.

In terms of the second challenge of CS,researchers have introduced plaintext keys and added scrambling and diffusion.Among them,DNA computation has been applied to the scrambling and diffusion process due to its great characteristics such as high parallelism,improved memory space,and very low power consumption (Song and Qiao,2015;Chai et al.,2017;Chen JX et al.,2018;Hu HH et al.,2018;Feng et al.,2019).Song and Qiao(2015)proposed an image encryption scheme by combining DNA coding technology with a CML system that uses a nonlinear logistic map.Chen JX et al.(2018)proposed a selfadaptive encryption algorithm using DNA random encoding and DNA XOR operations with a hyperchaotic Lorenz system.Hu HH et al.(2018) designed a parallel image encryption algorithm based on DNA sequence addition operation and complement operation,in which the chaotic sequence was generated by the integer chaotic system.Chen L et al.(2022) provided a medical privacy protection scheme based on chaos and DNA coding using two coupled chaotic systems to produce cryptographic primitives.These results illustrated that DNA computation could obtain good performance in image encryption.

Regarding the third challenge of CS for image encryption,Xie et al.(2016) initially proposed a model of semi-tensor product compressive sensing(STP-CS).The STP tool has been extensively applied to study Boolean networks,feedback shift registers,and some other problems(Lu et al.,2018,2021).The model breaks the dimension matching limit and thus reduces the space occupied by the measurement matrix.The STP-CS theory was then applied in image encryption for wireless body area networks by Li LX et al.(2019).As the size of the measurement matrix is reduced,the energy consumption of the sensor nodes in the network is reduced.Li LX et al.(2019) focused on the energy-saving characteristic of the STP-CS model,but here we use its parallel reconstruction feature to improve the decryption speed.

In this paper,we present a new scheme for image encryption that takes advantages of the NMLNCML system and DNA operations in CS.The proposed NMLNCML system strengthens the chaotic characteristics (e.g.,increased range of logistic map parameters,more stable randomness in Kolmogorov–Sinai entropy,and reduced number of periodic windows in bifurcation diagrams) of the system,which is very suitable for image encryption.We apply the NMLNCML system to generate the measurement matrix in CS and the pseudo-random sequence in DNA operations,which ensures the security of the encryption scheme.The STP-CS model with plaintext-related Arnold scrambling is used to effectively reduce the image redundancy information and measurement matrix storage,simultaneously implementing first-level encryption.The entire security is further enhanced by DNA random coding,DNA addition,and bit XOR operation.Simulation results show the effectiveness and superiority of the proposed image encryption scheme.

2 Proposed NMLNCML system

In our proposed scheme,an NMLNCML system withLlattices coupled by neighborhood links is defined as

wherei,j,kare different lattices (2≤i ≤L −1,1≤j,k ≤L),ηis the coupling parameter(0≤η ≤1),nis the time sequence (n=1,2,...),andf(x)is the logistic map satisfyingf(x)=μx(1−x) withμ ∈[3.56,4].Latticesjandkare both nonlinear neighbors of latticei,and the relationship amongi,j,andkis determined by an Arnold transform:

wherepandqare the parameters of Arnold mapping.

2.1 Kolmogorov–Sinai entropy

The NMLNCML system consists ofLlattices.For each lattice,it is a chaotic system,so the Lyapunov exponent(LE)(Wang XY and Liu,2020)values of each lattice can be computed.Without loss of generality,we apply Kolmogorov–Sinai entropy density(KED)hand Kolmogorov–Sinaientropy breadth(KEB)hu(Zhang YQ and Wang,2014) to describe the chaotic characteristics of the spatiotemporal chaotic system.hcan eliminate the influence of the number of lattices.The larger the value,the stronger the chaotic characteristics of the system.Whenhis 0,it means that the spatiotemporal chaotic system is behaving normally.huis employed to further describe the chaotic majority ofLlattices.The larger the value,the more lattices have chaotic behaviors,and thus the system exhibits stronger chaotic properties.

As in the MLNCML system (Zhang YQ and Wang,2014),we setL=100,p=12,andq=7 in our system.Figs.1 and 2 show the Kolmogorov–Sinai entropy comparisons between the proposed NMLNCML system and MLNCML system with differentμandηvalues.Figs.1b–1f and Figs.2b–2f show the chaotic situations of the MLNCML system from∊=0 to∊=0.8.

First,from Figs.1b–1f and Figs.2b–2f,it can be clearly seen that under different∊,the changes of Kolmogorov–Sinai entropy are not stable.The density and breadth of Kolmogorov–Sinai entropy in Figs.1c and 2c are lower than those in other subfigures,and the fluctuations are more intense.In the proposed NMLNCML system,the changes of Kolmogorov–Sinai entropy are stable (Figs.1a and 2a),because they are not affected by∊,which means that the chaotic property of the proposed system is more stable.Second,in the MLNCML system,the variation range of parameterμthat keeps the system in a chaotic state is [3.56,4],while in the NMLNCML system,the variation range ofμis [2.28,4],which is wider than that in the MLNCML system.Third,from the comparison between Fig.1a (Fig.2a) and Figs.1b–1f (Figs.2b–2f),it can be seen that the Kolmogorov–Sinai entropy of the proposed system is larger than that of the MLNCML system,and thus the chaotic property is stronger.In addition,without complex parameter selection,it is more user-friendly to set only the initial value of the chaotic lattice and the linear–nonlinear coupling parameterηto obtain the chaotic sequence.

Fig.1 Kolmogorov–Sinai entropy density comparison between the NMLNCML and MLNCML systems: (a)NMLNCML;(b) MLNCML (∊=0);(c) MLNCML (∊=0.2);(d) MLNCML (∊=0.4);(e) MLNCML (∊=0.6);(f)MLNCML (∊=0.8)

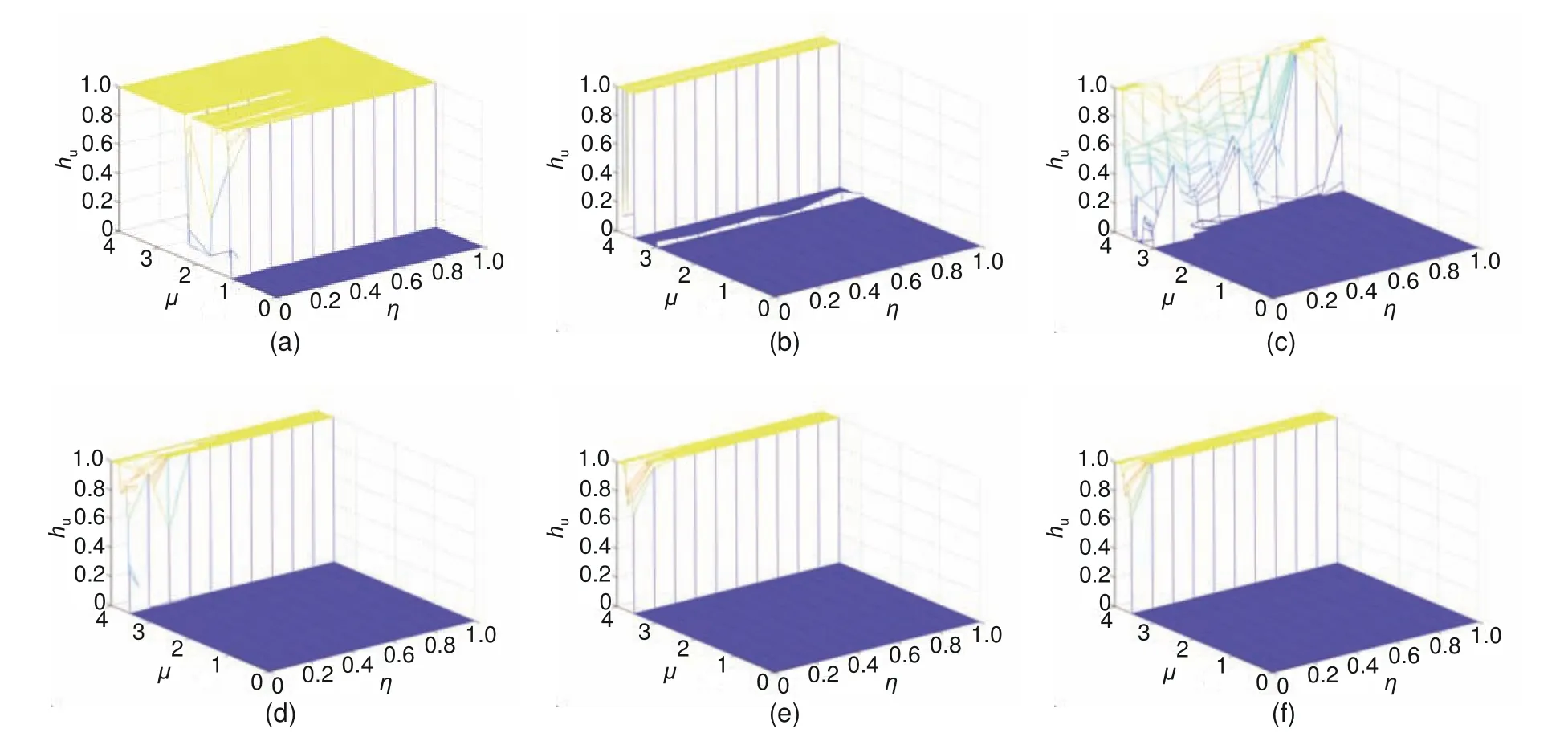
Fig.2 Kolmogorov–Sinai entropy breadth comparison between the NMLNCML and MLNCML systems: (a)NMLNCML;(b) MLNCML (∊=0);(c) MLNCML (∊=0.2);(d) MLNCML (∊=0.4);(e) MLNCML (∊=0.6);(f)MLNCML (∊=0.8)

2.2 Bifurcation diagrams

A bifurcation diagram describes a series of abrupt changes in the state of a dynamic system with the change of control parameters,such as the period-doubling bifurcation,which leads to chaos.Set the system parameters asL=100,p=12,q=7,and∊=0.5.Fig.3 shows the bifurcation diagrams of the MLNCML and NMLNCML systems withμ ∈[0,4] andη=0.3,0.5,0.7,0.9.From Figs.3b,3d,3f,and 3h,we can see that the MLNCML system contains many periodic windows whenμ ∈[0,3.56].Compared with the MLNCML system,although several values of parameterμmake the system non-chaotic in Figs.3a,3c,3e,and 3g,the range of optional parameterμin the NMLNCML has been enlarged from [3.56,4] to [2.28,4].Moreover,the number of periodic windows has decreased,and the chaos and ergodicity of the system have been significantly improved.

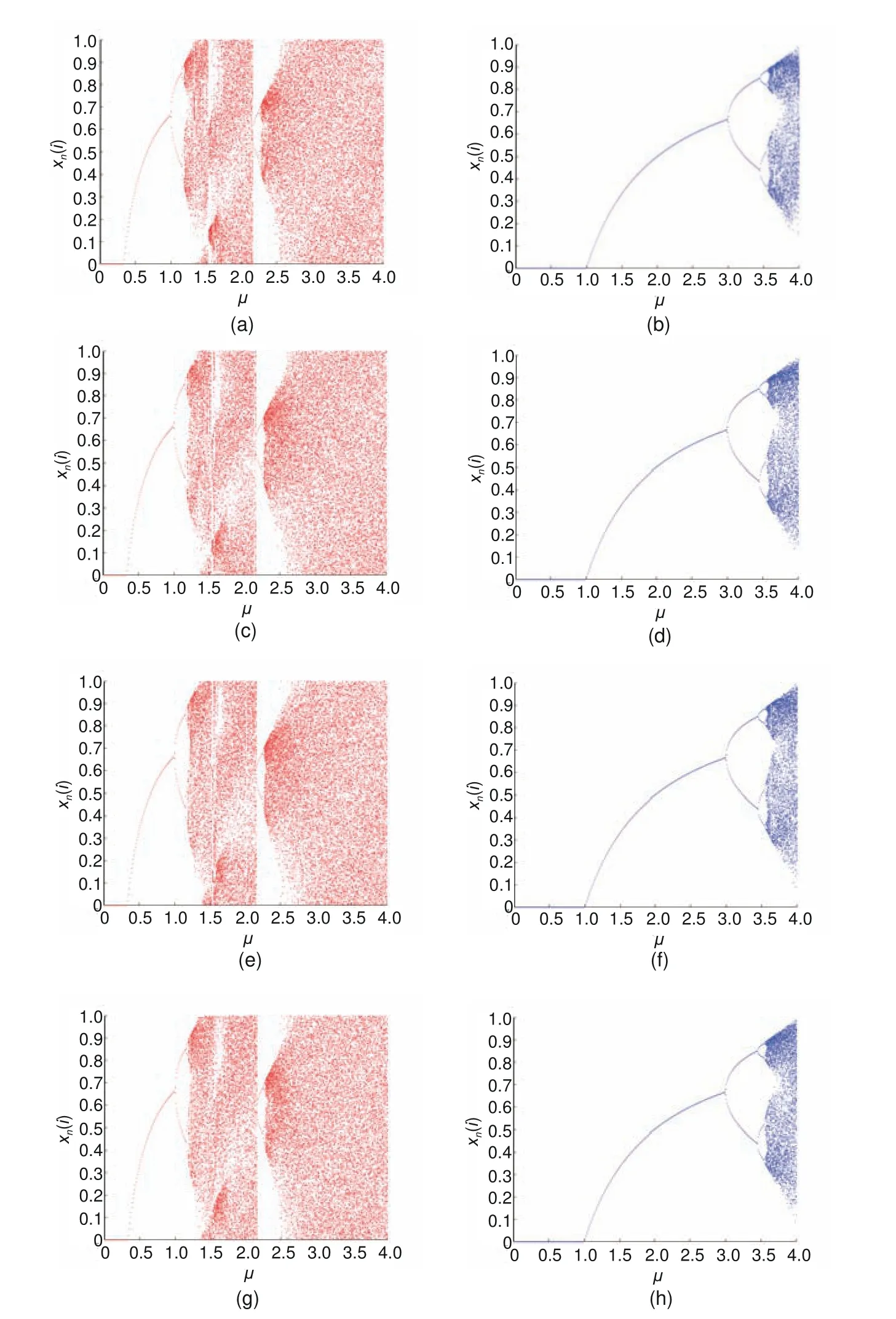
Fig.3 Bifurcation diagrams of the NMLNCML and MLNCML systems: (a) NMLNCML (η=0.3);(b)MLNCML (η=0.3);(c) NMLNCML (η=0.5);(d) MLNCML (η=0.5);(e) NMLNCML (η=0.7);(f) MLNCML(η=0.7);(g) NMLNCML (η=0.9);(h) MLNCML (η=0.9)

Because the forking of orbits in the NMLNCML system differs from that in the MLNCML system,we can further divide the value ofμin the NMLNCML system into two intervals,namely[0,1.5]and(1.5,4].It can be seen from Fig.3a that the NMLNCML system shows a similar bifurcation pattern whenμ ∈[0,1.5] with the MLNCML system whenμ ∈[0,4]from one period to two periods,to four periods,to eight periods,and so on.The explanation is that the direct weighting of the lattice and its linear–nonlinear neighbors accelerates the chaotic process of parameterμ,and the nonlinear modular operation harmonizes the distribution range of chaotic sequences,which enhances the ergodic property of the chaotic sequence.Due to the non-uniformity of the logistic functionf(x)and the further increase of parameterμ,some periodic windows still appear in the system whenμ ∈(1.5,4].This phenomenon is more obvious when increasingμto 2.16;that is,a new bifurcation of two periods to four periods appears in the NMLNCML system.However,due to the introduction of the coupling mode of the nonlinear modulus function,the distribution of the whole system is more uniform and the selection range of parameterμ,which causes the system to be chaotic,is expanded.The retention of nonlinear coupling parameterηinherits the chaotic behaviors of the MLNCML system.Parameterηincreases the randomness of the possible period of orbits,which leads to misleading and inconspicuous times of period-doubling bifurcation.The elimination of the coupling coefficient and the introduction of module operation changes the coupling method of the spatiotemporal chaotic system from linear coupling to nonlinear coupling,which further strengthens the chaotic characteristics of the system and greatly reduces the number of periodic windows of the spatiotemporal chaotic system.

3 Proposed image encryption algorithm

3.1 Plaintext-dependent key generation

To enhance the correlation between the plain image and the encryption scheme,an SHA-384 hash function is employed to generate the plaintextdependent keys.Taking a plain imagePas the input,the 48-decimal output of the hash functionHis computed.If one pixel value of the plain image changes,the hash value becomes much different.DividingHinto three parts to generate the real initial values for Arnold scrambling,Eq.(3) gives the computation process of the three parameterst,a,bin Arnold scrambling:

where parameterst0,a0,andb0are random positive integers given by a sender.Parametert0together with hash bits is used to produce the times of Arnold scramblingt.Parametersa0andb0as well as hash bits determine the real initial scrambling value of Arnold scrambling.Nrepresents the number of columns in the plain imageP.

3.2 Image compression and encryption algorithm

The whole flowchart of our encryption and decryption scheme is shown in Fig.4.The encryption algorithm conforms to the architecture of scrambling,compression,and diffusion.The detailed encryption process is introduced as follows:

Fig.4 Schematic diagram of the proposed encryption and decryption algorithm (DWT: discrete wavelet transform;STP-CS: semi-tensor product compressive sensing;NMLNCML: novel mixed linear–nonlinear coupled map lattice;IDWT: inverse discrete wavelet transform;SL0: smooth l0 norm)

Step 1:calculate the plaintext key parameterst,a,andbassociated with the original plain imageP1with size ofm×naccording to Eq.(3).

Step 2: perform discrete wavelet transform(DWT) on the plain image to obtain the sparsity coefficient matrixP2with the same size as plain imageP1via

Step 3: manipulate Arnold scrambling onP2to obtainP3of the same matrix size with parameterst,a,andbin step 1.Among them,parametertrepresents the number of times to perform Arnold scrambling,and parametersaandbare the scrambling parameters.

Step 4:iterate the NMLNCML system and generate chaotic sequences.As introduced in Section 2,first,set the initial values forx(1),x(2),...,x(L).Next,to ensure the chaos of the chaotic system,run the NMLNCML system (Npre+mn) times iteratively with the initial values,abandon the precedingNpretimes,and finally,Lpseudo-random sequences(x(1),x(2),...,x(L)) sampledmntimes are generated.The range of each sequencex(i) is (0,1) and these sequences are used in compression and diffusion in our encryption algorithm.In this study,we setNpreempirically to 1000.

The keysK1,K2,K3as well as a DNA initial valued(d ∈{“A,” “G,” “C,” “T”})set by the user are used as the real key values in the diffusion process.Among these keys,K1andK2are used to control the random encoding and decoding rules of DNA,whose values are 1–8.K3controls the binary XOR operation after DNA completion.dis the initial value in DNA addition.First,the compressed matrixP4in step 5 is decomposed to a binary sequence with sizem×8nand converted to the DNA sequenceP5with sizem×4nby random DNA encoding.For each two-bit transformation,the random coding rules are determined by the keyK1in Eq.(6).Then,DNA addition is performed on the encoded DNA sequenceP5to obtain the diffused DNA sequenceP6.A DNA addition rule is adopted and the addition is presented as in Eq.(10):

wherei=2,3,...,m×4nand “+” represents the DNA addition operation(Chen JX et al.,2018).Subsequently,the DNA sequenceP6is randomly decoding to a binary sequence with the keyK2in Eq.(7)and XORs the bits with the keyK3in Eq.(9)to obtain the final cipher imageP7.The image decryption process is the inverse of the encryption process.

3.3 Discussion

Our image encryption algorithm has the following merits.

First,a novel image compression–encryption algorithm based on STP-CS and DNA operations is introduced.The architecture of permutation,compression,and diffusion is adopted.The plain image is first converted into a coefficient matrix by DWT.Arnold scrambling is used to shuffle all elements of the coefficient matrix.Then the confused matrix is compressed by STP-CS,diffused by DNA operations and bit XOR operation,and the final cipher image is created.Because STP is introduced in CS,and the measurement matrix is smaller (in terms of a matrix’s dimension and the total number of elements in it) than the traditional CS,the computation overhead is reduced.Additionally,because of the structural properties of STP,the corresponding parallel reconstruction algorithm can further improve the speed of the decryption process.

In STP-CS,every column of the plain image is separately compressed,and thus,energy information is retained in each column.Energy leakage will occur,which reduces the security level of the algorithm.To solve this problem,DNA diffusion is added after the CS,which distributes energy uniformly in the whole cipher image.Therefore,the anti-statistical attack ability of the proposed encryption algorithm is improved and its security level is enhanced.

Second,a plaintext-dependent SHA-384 hash function is introduced to shuffle the sparse coeffi-cient matrix of the plain image.If any pixel in the original image changes,the hash value will be quite different.In permutation,the generation of initial scrambling parameters largely depends on the plain image,and different permutation processes will be obtained.Thus,our scheme can resist the CPAs and NPAs,which can compensate for the CS’s disadvantage.Because CS is a linear transform,the encryption schemes based on CS struggle to resist the CPAs and NPAs.

Third,an NMLNCML system is proposed with more stable structure and stronger randomness.Chaotic sequences generated by it are used in compression and diffusion processes of image encryption.The measurement matrix of STP-CS is obtained by the random sequence generated by one of the lattices and used in the compression process,and the keysK1,K2,andK3are attained by the arrangement and combination of sequences of other lattices and used in the DNA diffusion process.Compared with low-dimensional chaotic systems,high-dimensional spatiotemporal chaotic systems have more complex dynamics and more key parameters.Compared with the MLNCML system,the NMLNCML system is more stable and random.Thus,the corresponding image encryption scheme has a larger key space and a higher security level to resist brute-force attacks.

4 Simulation results

In this section,several simulations are carried out to realize the proposed image encryption algorithm and assess its performance.Three 512×512 gray images (Lena,Peppers,and Baboon images)are chosen as test images.All the simulations are conducted with MATLAB 2020a software on a personal computer with a 3.40 GHz CPU,8 GB RAM,and 64-bit Microsoft Windows 10.We use a two-level “Haar” wavelet to perform DWT.The initial values of key parameterst0,a0,andb0in Arnold scrambling are set to positive integers 52,12,and 7,respectively.The lattice numberLof the NMLNCML system is 10.Coupling parameterηis 0.8,andμin the logistic map is 3.99.Nonlinear neighbor parameters arep=7 andq=5.The initial values of each latticex(1),x(2),...,x(10) as part of keys in the NMLNCML system are 0.933 993 247 8,0.678 735 154 9,0.757 740 130 6,0.743 132 468 1,0.392 227 019 5,0.655 477 890 2,0.171 186 687 8,0.706 046 088 0,0.031 832 846 4,and 0.276 922 985 0.The DNA addition keyd0is selected as “C.” The reconstruction algorithm is smoothl0norm(SL0).

4.1 Encryption and decryption results

Fig.5 represents the simulation results of the Lena,Peppers,and Baboon images when the compression ratio CR=0.5(CR is the image volume ratio between the compressed cipher image and plain image).The size of the STP measurement matrix is 128×256.Figs.5a,5d,and 5g are three plain images of Lena,Peppers,and Baboon,respectively.Figs.5b,5e,and 5h are their corresponding cipher images.Figs.5c,5f,and 5i are the decrypted images.

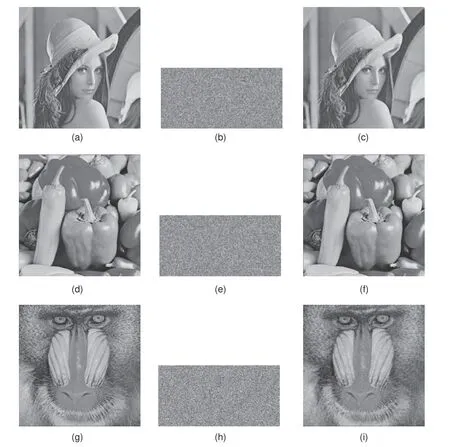
Fig.5 Results of encryption and decryption: (a) plain image Lena;(b) cipher image of (a);(c) decrypted image of (a);(d) plain image Peppers;(e) cipher image of (d);(f) decrypted image of (d);(g) plain image Baboon;(h) cipher image of (g);(i) decrypted image of (g)

As can be observed from Figs.5b,5e,and 5h,the cipher images are similar to noise images.There is no relationship between the original images and the corresponding cipher images,so we cannot obtain any useful information about the original images from the cipher images.Therefore,the proposed encryption algorithm can protect the original images.From Figs.5c,5f,5i,and their plain images,we can see that the decrypted images are similar to the original images.

To quantitatively measure the reconstruction quality of the decrypted image,the peak signal-tonoise ratio (PSNR) (Li LX et al.,2020) is used as an index to describe the similarity between the decrypted image and original image.The greater the value of the PSNR,the higher the quality of the decrypted image.

The PSNRs in Figs.5c,5f,and 5i with CR=0.5 are respectively 33.4462,33.7960,and 32.1523 dB,which are>30 dB,indicating the effectiveness of decryption.In summary,our algorithm has good encryption and decryption effect,and thus the cipher images could be safely transmitted and saved on public channels and networks.

4.2 Compression performance

To study the influence of CR on the quality of the decrypted image,we also use the PSNR to compute the reconstruction results with different CRs(0.25,0.50,and 0.75),as shown in Figs.S1 and S2 in the supplementary materials.Fig.S1 shows the encrypted images of Lena,Peppers,and Baboon with different CRs.Fig.S2 illustrates the reconstructed images with different CRs.The original images are shown in Figs.5a,5d,and 5g.As the CR decreases,the amount of the cipher image data that needs to be transmitted is reduced,but the quality of the decrypted image is also gradually degrading.However,from the last row in Fig.S2,even if the CR is 0.25,the details of the decrypted images are still clearly recognizable.In addition,Table 1 lists the PSNR values of our algorithm and other methods in Chen TH et al.(2016),Hu GQ et al.(2017),Li LX et al.(2019),and Gan et al.(2020) under the same CR(CR=0.5),and a 512×512 Lena image is chosen as the test image.From Table 1,we can see that the PSNR value in our cryptosystem is 33.4462 dB,which is greater than the values in Chen TH et al.(2016),Hu GQ et al.(2017),and Gan et al.(2020)and close to that in Li LX et al.(2019),indicating that our compressed encryption method has higher reconstruction quality.

Table 1 Comparison of PSNR values when CR=0.5

4.3 Robustness to noise and data loss

To test the robustness to noise and data loss,different intensities of Gaussian noise(GN)and salt and pepper noise (SPN) are added to the cipher image of Peppers (256×512 pixels,Fig.5e) first.Second,16×16,32×32,64×64,and 128×128 pixels are cropped for the cipher image of Peppers,and the corresponding decrypted images are shown in Figs.S3 and S4.

It can be seen from Figs.S3 and S4 that when GN (or SPN) with an intensity of 0.000 07 is added and 1/8 of the data are lost,the decrypted image can still be recognized.This shows that the encryption algorithm is robust to noise and data loss attacks.

4.4 Key space analysis

Generally speaking,an effective image encryption system should have enough key space to resist a brute-force attack.It was recommended in Alvarez and Li (2006) that the qualified keys of an image encryption system should be>2100≈1030to make all kinds of brute-force attacks invalid.For the suggested encryption method,secret keys are: (1) positive integerst,a,bdetermined by a 384-bit output of hash function and initial values oft0,a0,andb0;(2)the double-precision floating point initial state values of the NMLNCML systemx(1),x(2),...,x(10);(3) compressed quantization parameter valuesqmaxandqmin;(4) the DNA base symbol ofd0.In this study,we assume that the computational precision of the computer is 10−10,and the key space is,which is sufficiently large to withstand brute-force attacks.Table 2 gives the key space of different algorithms in Zhang YQ et al.(2016),Li LX et al.(2019),Wen et al.(2020),and Li XH et al.(2022).It can be seen that the key space in our scheme is much larger than that of other algorithms,but smaller than the key space in Li XH et al.(2022).

Table 2 Comparison of key space

4.5 Key sensitivity analysis

Key sensitivity is an essential indicator to verify the effectiveness of a cryptosystem,and it can be analyzed from two perspectives: (1) from the perspective of the decrypter,completely different cipher images should be obtained as a result of a slight difference in encryption keys;(2) from the perspective of the encrypter,the plain image should not be correctly recovered even if the decryption keys and encryption keys are nuanced.

The plain image Lena is used for demonstration when CR=0.5.For the first case of key sensitivity assessment,key sensitivity tests are performed during encryption.The correct encryption keys were introduced in Section 4.4 as (1) the 384-bit output of the hash of Lena is“7620c8d5c7eafdab5fc1c0ba1fc09947ce4645de44ba41 f9ed222968b9108fe92371a5e26f3130ab893a554380ff1 ee9,”t0=388,a0=12,b0=7;so,t=53,a=41,andb=84.(2)L(L=10) initial values of latticex(1),x(2),...,x(L) are respectively set as 0.933 993 247 8,0.678 735 154 9,0.757 740 130 6,0.743 132 468 1,0.392 227 019 5,0.655 477 890 2,0.171 186 687 8,0.706 046 088 0,0.031 832 846 4,and 0.276 922 985 0.(3) Compressed quantization parameter values areqmax=1.906 691 698 0,qmin=−2.295 009 277 4.(4)d0=“C.” These keys are used to generate the default cipher image shown in Fig.5b.Then,after a slight change of 10−10tox(1),x(2),x(5),x(9),andx(10),the comparison of the cipher images is shown in Fig.S5.The pixel difference ratios between the default cipher imageand other cipher images are computed and given in Table S1 in the supplementary materials.It can be seen that there is no similarity between the cipher images,and a small change in the encryption keys will cause>99.55% of pixels to become different in cipher images.

Next,we test the sensitivity of the key from the perspective of the decrypter for the second case.In the decryption process,we use the same key as in the encryption process.Fig.5c is the recovered image decrypted with the correct key,and Fig.S6 shows the images decrypted with subtly modified keys.The pixel differences between the disordered decipher images and the correct image are 99.8543%,99.8474%,99.8558%,99.8253%,and 99.8405%.

Considering the above two aspects,we can see that even a tiny interference of the keys will result in significant difference in the output of encryption or decryption,so the proposed encryption algorithm is highly sensitive to the secret key,and no valuable information about the key and plaintext will be leaked.

4.6 Statistical attack

Statistical attacks are used to analyze and decipher an encryption system by counting the characteristics of the cipher image in terms of histogram,pixel correlation,and information entropy (Zhang LY et al.,2018).The image histogram reflects the most basic statistical characteristics of the image.Correlation coefficientrxybetween adjacent pixels reflects the performance of the scrambling process in a cryptosystem.The lower the correlation between adjacent pixels of cipher images,the better the scrambling effect of the encryption algorithm.Information entropy is a vital indicator used to measure whether the gray value distribution in an image is uniform.The greater the information entropy of the image,the more uniform the gray value distribution of the image,and the greater the possibility of resisting entropy attacks.In theory,if the probability of each pixel value is equal,the maximum value of information entropy is ideally eight.

Fig.S7 shows the histogram information of the three original images and their corresponding cipher images(CR=0.5).It is obvious that the histograms of the cipher images are distributed uniformly over the interval [0,255] and are significantly different from those of the plain images.

In our simulation,3000 pairs of adjacent pixels are randomly selected from the horizontal,vertical,and diagonal directions,separately.Fig.S8 illustrates the correlation distributions of two adjacent pixels in the horizontal,vertical,and diagonal directions of the image Lena.Table S2 shows the results of the correlation coefficientrxyof the plain images and their corresponding cipher images.As can be observed,the correlation between adjacent pixels in the original image before encryption is very strong,but the correlation after encryption is greatly reduced.

Table S3 lists the information entropies of plain images and their corresponding cipher images when CR=0.5.It can be seen from this table that information entropies of cipher images are all>7.99 and have increased more than that of their plain images.Table S4 presents the comparison with other encryption algorithms,and a 512×512 Lena image is used to test the performance.From Table S4,one may derive that our cryptosystem has good performance compared with Gan et al.(2020),and has better performance than Li LX et al.(2019),Chai et al.(2020a),and Li XH et al.(2022).

The above results prove the strong randomness of different encrypted images,showing the negligibility of information leakage in encryption and further demonstrating that the proposed cryptosystem is secure enough to resist entropy attack.

4.7 Differential attack

In a differential attack,an attacker makes specific changes to the plain image and then compares the corresponding ciphertext to obtain clues about the secret keys.To resist differential attacks,encryption algorithms usually need to have good diffusion performance;that is,a small modification of the original image will bring about significant disturbance in the ciphertext.The number of pixel change rate (NPCR) and unified averaged changed intensity (UACI) (Chai et al.,2022a)are usually used as numerical indicators to evaluate the ability of encryption algorithms.

To test the resistance to a differential attack,the Lena,Peppers,and Baboon images are chosen,the first,last,and a random pixel of each are changed,and different cipher images are obtained with the same keys.Table S5 lists the NPCR and UACI results between different cipher images and their corresponding default cipher images.As can be seen from Table S5,the NPCR and UACI values under different conditions are close to the expected values 0.996 094 and 0.334 635(Wu Y et al.,2011),suggesting that the proposed encryption system has good diffusion properties expressly to resist the differential attack.

4.8 Known-and chosen-plaintext attack analyses

Our image encryption algorithm is designed to resist the CPA and NPA,because of the following two aspects:

On one hand,the Arnold scrambling process is related to the plain image.This is because the SHA-384 function and secret keys together determines the parameters of Arnold scrambling.When any bit of the plain image changes,even if the same secret key is used,different output of the SHA-384 function will be generated.Thus,the scrambling process is distinct,making it infeasible to decrypt other cipher images using the key streams retrieved with a welldesigned plain image from the attacker’s point of view.

On the other hand,because STP-CS is essentially a linear transform,a single STP-CS is unable to resist the CPA and NPA.This is because if an attacker selects an identity matrix as the plaintext,the information of the measurement matrix will be leaked.Therefore,we design the diffusion phase after compression.In the diffusion phase,we adopt chaotic sequence-controlled DNA random coding/decoding,DNA addition,and bit XOR operation,combined with the plaintext-related scrambling stage,to achieve one-time encryption,which is resistant to CPA and NPA.

4.9 Computational and complexity analyses

To evaluate the computational time of our image cryptosystem,tests are performed on 512×512 Lena,Peppers,and Baboon images.Simulations on different images are separately encrypted and decrypted 10 times by our algorithm when CR=0.5 and STP measurement matrices are with the dimension of 128×256.The total average encryption time is 1.9352 s and decryption time is 14.9216 s.Figs.S9 and S10,respectively,show the proportion of time spent in each phase of the encryption and decryption processes.The comparison results of the encryption time between our scheme and other methods for plain images of 512×512 are listed in Table S6.

For the execution time of our algorithm in Fig.S9,the most time-consuming encryption parts are DNA diffusion and Arnold scrambling.The time complexity of Arnold scrambling isO(tMN),wheret(t≤N) represents the number of scramblings,andMandNrepresent the numbers of rows and columns of an image,respectively.The DNA diffusion,which takes most of the time,includes DNA random encoding,DNA addition,DNA random decoding,and bit XOR operation.The time complexities are as follows: DNA random encoding,O(MN)+O(4MN);DNA addition,O(4MN);DNA random decoding,O(4MN)+O(MN);bit XOR operation,O(MN).Therefore,the time complexity of DNA diffusion isO(15MN).

The iterative process of chaotic systems,although running 263 144 steps,with the time complexity ofO(LMN),does not require too much time.One reason is that the chaotic system involves no computationally complex functions,such as the sine map used by Peng et al.(2021),cosine and exponential maps,etc.Another reason is that the number of coupled mapped grids set in our system is 10,which is relatively small.That means when the size of lattices is designed properly,the running speed of our algorithm could increase accordingly.From Table S6,we can see that our encryption algorithm is faster than Chai et al.(2020b),Gan et al.(2020),and Li XH et al.(2022),close to Li LX et al.(2019),and slower than Chai et al.(2020a),indicating the efficiency of the proposed algorithm.

In the decryption process,in addition to confusion and diffusion,the image reconstruction process occupies a larger proportion.This is because the SL0 algorithm takes a long time in the convergence phase.However,STP-CS can improve the signal recovery speed by grouping image coefficients,and each group can run the SL0 algorithm at the same time.By shortening the reconstruction time,the total speed of the proposed decryption algorithm is increased.As shown in Table S7,for a 512×512 Peppers image,when CR=0.5,we set the measurement matrix of different sizes,and record the time consumed for reconstruction.

As the size of the STP measurement matrix decreases,the time spent on the reconstruction algorithm also decreases.When the numbers of rows and columns of the measurement matrix are 1/8 of the traditional measurement matrix,the time of the reconstruction algorithm is about 1/4 of the traditional reconstruction algorithm.Therefore,the proposed algorithm is effective.

5 Conclusions

This paper proposed a new scheme for image encryption that took advantages of the NMLNCML system and DNA operations in CS.The proposed NMLNCML system continued the outstanding properties of the MLNCML system and further strengthened the chaotic characteristics(e.g.,increased range of the logistic map parameter,more stable randomness in Kolmogorov–Sinai entropy,and reduced number of periodic windows in bifurcation diagrams) of the MLNCML system,which was very suitable for image encryption.We employed the NMLNCML system to generate the measurement matrix in CS and the pseudo-random sequence in DNA operations,which ensured the security of the encryption scheme.The STP-CS model with plaintext-related Arnold scrambling was used to effectively reduce the image redundancy information and measurement matrix storage,which simultaneously implemented a first-level encryption.The entire security was further enhanced by DNA random coding,DNA addition,and bit XOR operation.In the decryption process,the introduction of STP also greatly reduced the decryption time.Simulation results and security analysis indicated that our cryptosystem has significant key space,high sensitivity to secret keys,great resistance to chosen-plaintext,statistical,and differential attacks,and good robustness to noise and data loss.In addition,the outstanding compression and encryption performance can promote secure image compression and transmission on public channels and networks.However,the speed of DNA encryption and STP reconstruction is relatively low in the proposed scheme.In our future research,we will study how to improve the efficiency of these two parts.

Contributors

Yuanyuan LI and Xiaoqing YOU designed the research.Yuanyuan LI,Xiaoqing YOU,Jianquan LU,and Jungang LOU processed the data.Yuanyuan LI,Xiaoqing YOU,and Jungang LOU drafted the paper.Jianquan LU helped organize the paper.Yuanyuan LI,Xiaoqing YOU,Jianquan LU,and Jungang LOU revised and finalized the paper.

Compliance with ethics guidelines

Yuanyuan LI,Xiaoqing YOU,Jianquan LU,and Jungang LOU declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

List of supplementary materials

Fig.S1 Cipher images under different compression ratios(CRs)

Fig.S2 Decrypted images under different CRs

Fig.S3 Cipher and decrypted images under different intensi

ties of Gaussian noise (GN) and salt and pepper noise (SPN)attacks

Fig.S4 Cipher and decrypted images under different degrees of data loss attacks

Fig.S5 Key sensitivity test in the first case

Fig.S6 Key sensitivity test in the second case

Fig.S7 Histogram information for plain and cipher images

Fig.S8 Correlation distributions of image Lena and its cipher image

Fig.S9 Time proportion of different encryption phases

Fig.S10 Time proportion of different decryption phases

Table S1 Differences between cipher images produced by slightly different keys

Table S2rxyof adjacent pixels in the plain and cipher images

Table S3 Information entropies of plain and cipher images

Table S4 Information entropy comparison among different methods

Table S5 Differential attack resistance of the proposed scheme

Table S6 Encryption time comparison among different methods

Table S7 Reconstruction time comparison among different semi-tensor product measurements