基于GM-RBF不定权组合模型的输电线塔杆倾斜预测分析与应用
王洪武, 李俊鹏, 张继伟, 黄 然, 朱 宇, 宋 宝
(1.云南电网有限责任公司 输电分公司,云南 昆明 650033; 2.云南电网有限责任公司 电力科学研究院,云南 昆明 650217; 3.北京空间飞行器总体设计部,北京 100094; 4.安徽理工大学 空间信息与测绘工程学院,安徽 淮南 232001)
输电线路塔杆是输电线路与地面搭接的构筑物,是电力系统的重要组成部分,其安全状态是影响电力系统运行的重要因素。输电线塔杆易因自然环境条件或人为破坏等因素发生沉降、倾斜,危及人们的生命财产安全,造成电力故障[1-3]。国内外诸多学者针对输电线塔杆倾斜姿态问题进行了一系列研究,文献[4-7]提出采用力学分析方法研究风对塔杆的影响,分析塔杆在风作用下的动态特性和稳定性状态;文献[8-11]提出利用各类传感器对塔杆的异常情况进行监测。但是缺少对塔杆的结构进行异常监测的方法和模型,而且只能间接反映塔体发生较大变形时的应力,不能及时发现负荷平衡参数、隐蔽故障(如塔体微小形变)或局部杆件的屈服失效。因此,建立一个输电线塔杆倾斜姿态预测模型,快速及时地获取塔杆的倾斜情况,并准确获得相关塔杆的具体位置成为电力系统亟待解决的问题。使用北斗高精度定位数据,构建铁塔预测模型及时准确地实时监测塔杆的倾斜姿态变化情况,来解决上述存在的问题十分必要。
本文使用北斗逆向网络载波相位差分技术(real-time kinematic,RTK)数据,基于不定权的灰色模型-径向基函数(grey model-radial basis function,GM-RBF)神经网络加权组合预测模型对铁塔姿态进行预测,不但避免了灰色模型(grey model,GM)预测方法存在的理论误差,提高了神经网络的训练速度和预测精度,更加减弱了定权加权组合模型对铁塔的倾斜姿态整体预测精度的影响。有利于精确地对电力铁塔倾斜进行全天候监控、预警,以满足电力信息化支撑功能的需求,保障输电线路的安全运行。
1 GM-RBF组合模型
1.1 GM模型
常见的灰度预测模型有GM(1,1)、GM(2,1)、DGM和Verhulst模型[12]。其中,GM(1,1)模型是一阶微分方程,只含有1个变量的灰色模型,适用于有较强指数规律的序列;另外3个预测模型适用于预测具有饱和的S形序列或者单调的摆动发展序列缺陷。
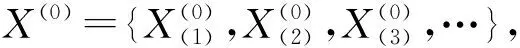
(1)

(2)
其中:a为预测系统的发展系数;b为灰度作用量。
因此,可得到GM(1,1)的时间响应函数为:
(3)
最后通过累减得到预测值为:
(4)
1.2 径向基函数神经网络
径向基函数(radial basis function,RBF)神经网络是一种具有单隐层的3层前馈网络的神经网络,其网络结构如图1所示。

图1 RBF网络结构
RBF神经网络是一种性能良好的前向网络,其激励函数一般是高斯函数。具有最佳逼近、训练简洁、学习收敛速度快以及克服局部最小值问题的性能,目前已经证明RBF神经网络能够以任意精度逼近任意连续的函数,且具有全局逼近能力,从根本上解决了BP(back propagation) 神经网络的局部最优问题,而且拓扑结构紧凑,结构参数可实现分离学习,收敛速度快。因此已经被广泛应用于模式识别、非线性控制和图像处理等领域[15]。
使用RBF神经网络方法,建立如下网络:
net=newrb(t,x(0),goal,spread)
(5)

(6)
1.3 GM-RBF加权组合模型
GM预测模型对于非线性问题的求解精度和长期预测精度等方面存在不足,RBF神经网络预测模型具有收敛速度偏慢和数据利用率低等缺点,因此本文对2种预测模型进行优化组合,综合2种模型的优势提出一种GM-RBF组合预测模型。
实际中, 由于输电塔杆变形呈非线性、不稳定性和随机性变化, 使得各个单一模型对各期的预测结果都有所不同, 而权值的比重直接影响组合模型的预测精度。因此本文探讨了2种不同的加权组合模型,结构框架如图2所示。
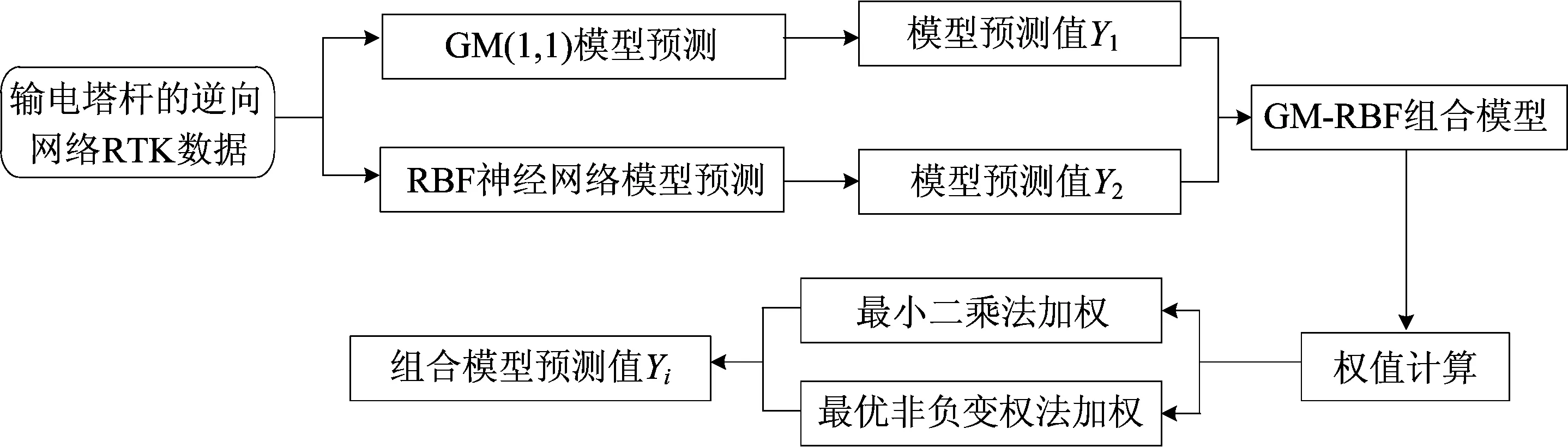
图2 GM-RBF加权组合模型数据流程图
1.3.1GM-RBF最小二乘法定权组合模型
首先针对原始的变形监测数据序列分别进行GM预测模型和RBF神经网络预测模型建模;然后通过精度评定分析其预测精度是否合格,若精度不合格则重新对原始数据进行建模,反之则进行下一步对2个模型进行优化组合;最后利用构建的组合模型生成出最终变形预测值。在最小二乘加权组合中,利用最小二乘的方法来确定每个模型的预测权重,具体过程如下:设GM预测模型的变形数据预测值序列为GMi={GM1,GM2,GM3,…},RBF神经网络预测模型的变形数据预测值序列为RBFi={RBF1,RBF2,RBF3,…},i=1,2,3,…,n。由此可以得到预测值与实测值之间的残差v为:

(7)
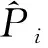
(8)
也可改写成:
VTV=min
(9)
此外,可以将(7)式写成:
V=BX-L
(10)
其中
根据(9)式可解算位置参量X为:
X=(BTPB)-1BTPL
(11)
其中,P为观测值权阵,为n×n的单位矩阵。
1.3.2GM-RBF不定权组合预测模型
相较于单一的预测模型,GM-RBF不定权组合预测模型与GM-RBF最小二乘定权组合预测模型一样,均综合了各个预测模型的优点,从而达到优化预测结果的目的。然而,对于GM-RBF最小二乘定权组合模型而言,模型中确定的权值a、b是恒定不变的,由此得到的预测值不能很好地反映输电塔杆的变形状况。因此,GM-RBF不变权组合预测模型可以很好地消除这一弊端,其获取的权值是变动的。具体过程如下。
设输电塔杆的实际变形值为Yt,GM与RBF预测模型得到的预测值记为Yt_m。其中:m为预测模型类别,m=1代表GM预测模型,m=2代表RBF预测模型;t为预测时期,t=1,2,…,n。可得:
(12)
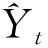
(13)
其中:m=1,2;t=1,2,…,n。
设et_m、et分别为m模型与组合模型在第t时期的输电塔杆预测误差,则有:
[Wt-1Wt-2][et-1et-2]T
(14)
可以得出:
[et-1et-2][Wt-1Wt-2]T=
(15)
其中
Wt=[Wt-1Wt-2]T;
Et=[et-1et-2]T[et-1et-2]=
(16)
由此可确定最优变权系数的规划模型,即
minf=WTEW
(17)
(18)
其中,Rn=[1 … 1]T。
2 输电塔杆倾斜测量模型
根据塔杆结构,可将塔杆的倾角、塔高与面位移之间的关系进行简化,模型如图3所示。

图3 塔杆倾角、高度与面位移的关系模型
根据图3塔杆的参数关系,可以得到塔杆面形变量ΔP的计算公式为:
(19)
其中:ΔX为X方向的形变量;ΔY为Y方向上的形变量。计算公式为:
(20)
其中:(Xi,Yi)为当前测量点坐标;(X0,Y0)为初始测量点坐标。
由图3可知倾角θ的计算公式为:
θ=arcsin(ΔP/H)
(21)
其中,H为当前塔杆高度。
3 实验与讨论
3.1 样本数据与预测效果分析
为验证优化GM-RBF不定权组合预测模型的预测精度及其有效性,以及更好地评价模型确切的精度指标,本文以昆明市某地区一处输电塔杆2020年12月1日至2021年5月2日的北斗逆向网络RTK数据为例,该监测点的监测数据共有200期,分别采用GM预测模型、RBF神经网络预测模型、GM-RBF最小二乘定权组合预测模型和GM-RBF不定权组合预测模型对铁塔监测数据的前100期数据建模,在模型建立成功后,利用已建立的模型预测后100期的变形量,然后将预测值与实测值进行比较,计算模型的残差,检验模型的精度。
铁塔的部分监测数据见表1所列。
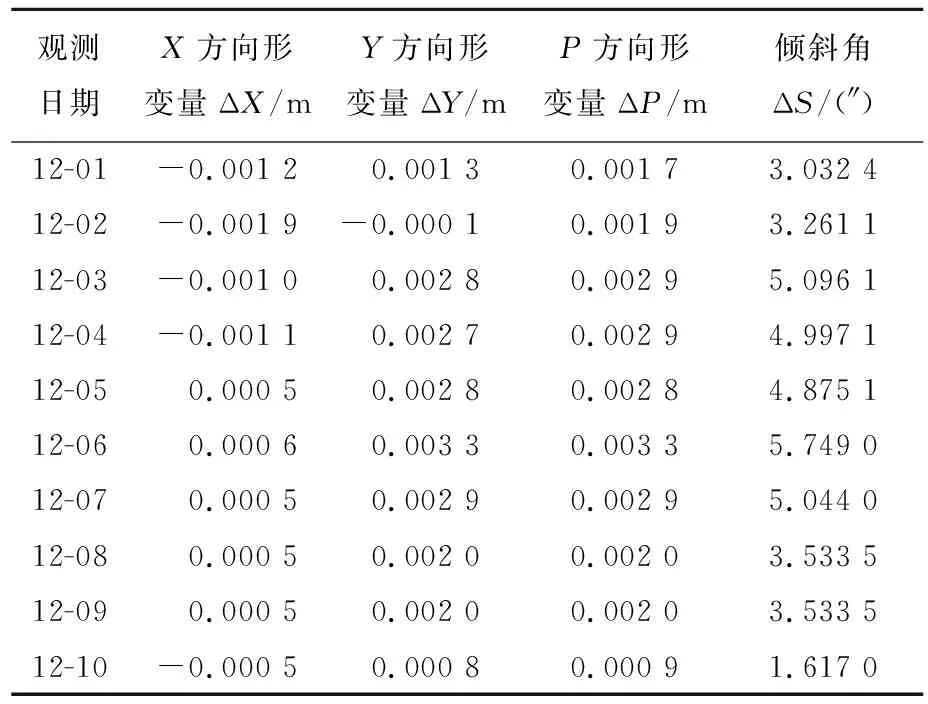
表1 铁塔前100期在不同方向上的形变量及倾斜角
表1中,观测日期为2020年12月1日至2020年12月10日。GM预测模型、RBF神经网络预测模型和2种加权GM-RBF组合模型预测值与实测值比较如图4所示。从图4可以看出,在预测的100期的数据中,在X、Y、P方向和塔杆倾斜角预测值在约为20期处发生转折变化。其中,前2期GM预测模型精度和GM-RBF不定权组合预测模型精度相当,均优于RBF神经网络预测模型和GM-RBF最小二乘定权组合模型,其中在X方向上的效果最为明显;后80期的预测中,GM预测模型、RBF神经网络预测模型和GM-RBF最小二乘定权组合预测模型的预测值偏于实测值,GM预测模型的预测值与实测值偏离较大,RBF神经网络预测模型和GM-RBF最小二乘定权组合预测模型预测效果优于GM预测模型。整体从100期的预测效果看,GM-RBF不定权组合预测模型明显优于GM预测模型、RBF神经网络预测模型和GM-RBF最小二乘定权组合预测模型。

图4 4种模型预测值与实测值比较
3.2 预测精度分析与评价
为了量化地对比分析4种模型的预测精度,定义如下2个误差指标。
均方根误差计算公式为:

(22)
平均绝对偏差计算公式为:
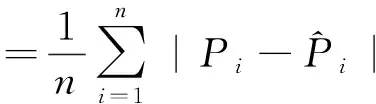
(23)
根据(22)式、(23)式计算4种模型残差的均方根误差和平均绝对偏差,如图5所示,见表2所列。图5中日期为2021年。前20期对于输电塔杆的各项参数预测中,GM-RBF不定权组合预测模型和GM预测模型在X、Y、P方向和塔杆的倾斜角预测上的均方根误差相差幅度不大,精度表征效果相当。然而,在X、Y、P方向和塔杆的倾斜角预测上的它们的均方根误差优于RBF神经网络预测模型分别为22.92%、10.87%、1.14%、0.36%;优于GM-RBF最小二乘定权组合预测模型结果为23.46%、11.79%、0.58%、0.28%。

表2 4种预测模型在X、Y、P方向与倾斜角预测精度比较

图5 4种模型预测值与实测值偏差
从100期对于输电塔杆的长周期各项参数预测中可以看出,GM-RBF不定权组合预测模型精度最优,RBF神经网络预测模型精度次之,GM-RBF最小二乘定权组合预测模型精度较低,GM预测模型最低。其中,GM-RBF不定权组合预测模型在X、Y、P和倾斜角的预测精度分别优于GM预测模型约57.28%、48.07%、43.02%、42.08%,优于RBF神经网络预测模型约2.04%、2.31%、3.60%、2.02%,优于GM-RBF最小二乘定权组合预测模型约2.97%、2.36%、6.23%、4.73%。
此外,从横向对比看出,无论是短期还是长期的4种模型在X、Y方向的预测中,Y方向的预测均方根误差要明显高于X方向的预测均方根误差,造成这种现象的主要原因是GM预测模型和RBF神经网络预测模型的预测均取决于前期的监测数据,前期监测数据的稳定趋势决定预测值的稳定性。结合前100期的监测数据中,X方向的监测值变化趋势较平稳,起伏不大,然而在Y方向的监测值起伏剧烈,趋势变化明显,无规律,因此,在后100期数据的预测中,体现出Y方向预测的均方根误差相对较大。
综上所述,在短周期输电塔杆的各项参数预测中,GM预测模型和GM-RBF不定权组合预测模型的预测效果较好;在长周期输电塔杆的各项参数预测中,GM-RBF不定权组合预测模型的预测精度最优。因此,GM-RBF不定权组合预测模型得到输电塔杆倾斜姿态的预测结果最接近实测值。
4 结 论
本文通过对GM模型和RBF神经网络2种预测模型进行分析,提出了一种GM-RBF不定权组合预测模型。结合相关实例,得出如下结论:
(1) 在短期对于电力塔杆倾斜预测中,GM预测模型的精度与GM-RBF不定权组合预测模型精度相当,优于RBF神经网络预测模型和GM-RBF最小二乘定权组合预测模型。其中,GM预测模型与GM-RBF不定权组合预测模型在X、Y、P3个方向和塔杆整体倾斜角的预测精度优于RBF预测模型约22.92%、10.87%、1.14%、0.36%;优于GM-RBF最小二乘定权组合预测模型约23.46%、11.79%、0.58%、0.28%。
(2) 在长期对于电力塔杆倾斜预测中,GM-RBF不定权组合预测模型精度最优,RBF神经网络预测模型精度次之,GM-RBF最小二乘定权组合预测模型精度较低,GM预测模型最低。其中,在X、Y、P3个方向和塔杆整体倾斜角的预测精度上优于GM预测模型约57.28%、48.07%、43.02%、42.08%;优于RBF神经网络预测模型约2.04%、2.31%、3.60%、2.02%;优于GM-RBF最小二乘定权组合预测模型约2.97%、2.36%、6.23%、4.73%。
总体上,在对输电塔杆的倾斜预测中,不论是短期还是长期预测,GM-RBF不定权组合预测模型预测值更接近实测值。因此,GM-RBF不定权组合预测模型有着较高的预测精度,更有利于输电塔杆的倾斜姿态预测。

