表面粗糙度对NIR预测落叶松基本密度的影响

王志远，李耀翔，张哲宇

（东北林业大学 工程技术学院，黑龙江 哈尔滨 150040）

近红外分析技术凭借着快速方便、绿色无损的优势在农业、食品药品以及石油化工等产业快速发展，获得了科研人员的青睐[1-3]。在林业方面，近红外被应用于木材的物理、化学、力学性能的测定[4]，Chen 等[5]提出了一种利用Vis-NIR 高光谱成像和改进随机青蛙算法（MRF）预测木材含水率的新方法；曾韦珊等[6]利用近红外光谱技术建立了湿加松针叶儿茶素和表儿茶素总量的模型；Chen 等[7]采用正交偏最小二乘法（OPLS）和连续投影算法（SPA）提取有效光谱，并采用混合偏最小二乘法（MIX-PLS）建立预测木材弹性模量的模型；蔡绍祥等[8]通过傅里叶变换红外光谱分析木材细胞壁化学成分变化情况，研究不同木材化学成分对细胞壁静态黏弹性的影响。为保证近红外技术预测结果的准确性，需要尽可能地减少各种因素对近红外光谱的影响，其中主要因素包括实验样品因素、仪器因素、实验操作人员因素。

近红外仪器是近红外分析的基础硬件，按分光类型可分为滤光片型、光栅色散型、傅里叶变换型等，按应用类型分为实验室型、便携型和工业在线型。不同类型的仪器会产生较大差异，即使在测量相同材料时也会产生略有不同的光谱。Yap 等[9]提出的自适应人工神经网络算法可以在没有标准样品参与的情况下将主仪器的模型转移到其他仪器上，降低了校准模型的成本；Mcvey等[10]比较了台式近红外仪器、便携式近红外仪器和手持SCIO 仪器3 种仪器预测芫荽种子真实性的能力，与台式近红外仪器相比，另外2 种仪器存在一些局限性；Wolfrum 等[11]比较了常规实验室近红外（NIR）光谱仪和两个低成本NIR 光谱仪的性能，表明与传统的实验室光谱仪相比，使用光谱范围有限的低成本光谱仪具有很大的前景。

实验操作人员装样方式的选取、制样方法的不同、采集样品的方式、操作熟练度等都会在一定程度上影响模型精度。Costa 等[12]发现不同的光谱采集技术对近红外模型预测木材密度具有影响，由积分球采集的光谱生成的NIR 模型比光纤具有更好的统计数据；Dos Santos 等[13]同样分析了积分球采集和光纤采集对建立近红外光谱模型预测木材含水量的影响，结果显示用积分球在木材表面上采集的近红外光谱最适合生成用于估计桉树木材含水量的近红外模型；Li 等[14]研究了在不同的角度采集光谱对预测结果的影响，证明90°角（横向）模型或混合角度模型可以为基本密度预测提供一个可靠的结果。实验结果在很大程度上取决于操作员的经验和知识，根据标准和使用指南进行操作，可以减少不同批次实验的误差[15]。

实验样品因素是比较主要的影响因素，样品的含水率、温度以及化学成分组成都会不同程度影响光谱的准确性。Ayanleye 等[16]发现木材表面状况会极大地影响预测模型的性能，当木材表面粗糙时，可以获得更好的性能；黄安民等[17]证明建立不同粗糙度的混合预测模型可以减少粗糙度对模型的影响，提高模型的稳健性；Kunze 等[18]证明外部参数正交化（EPO）可以校正不同水分条件下巴西本土树种木材光谱中水分的影响，并通过PLS-DA 判别模型进行分析，在PLS-DA 识别样本时采用更灵活的标准也有利于减少误差。样品的粒径已被证明对湿化学分析、化学降解和光谱信息的结果有很大影响[19]。Wu 等[20]研究了不同粒径对土壤有机质光谱预测的影响，发现混合样品可以提高土壤样品的表面反射率，增加与土壤有机质的相关性。

为了去除一些无关信息或噪声的影响，提高模型的预测精度，选择合适的仪器、光谱范围、建模方法、光谱预处理和代表性样品至关重要。Li等[21]在提升小波变换的基础上，利用双正交小波对最优变换的光谱进行分解；Pasquini 等[22]评估了一种可提高紧凑型近红外分光光度计性能的旋转线性样品探测装置，该装置使测量过程中评估的样本量最大化，提供了更具代表性的平均光谱，显著改善了多元回归结果；Wu 等[23]提出了一种改进加权乘法散射校正算法进行变量选择，与其他校正方法相比，其可以提供更好的预测性能。

木材的基本密度是一项重要的物理性质，与其力学性能息息相关，在木材加工利用和干燥防腐中具有实际意义[14]。本研究以东北地区的落叶松为研究对象，分析不同表面粗糙度对近红外光谱技术预测落叶松木材基本密度的影响，采用波段选择的方法优选出特征波段，根据优选波段建立基本密度预测模型，达到优化近红外模型的目的，减小表面粗糙度对预测精度的影响。

1 材料与方法

1.1 试验材料

试验样本采自黑龙江省方正县高楞镇星火林场(N45°43′5.73″，E129°13′34.37″)。星火林场的土壤类型为暗棕壤森林土，在落叶松天然次生林区，分别设立4 块大小为20 m×20 m 的样地，在每块样地的向阳面和背阴面随机选取一棵标准木；伐倒后，用电锯自标准木胸径（胸高1.3 m 处）开始，向上连续锯截5 cm 左右圆盘，在实验室对木圆盘进行手工剥皮后，过树芯由北向南锯截2 cm×2 cm×3 cm 的木块，共计120 个落叶松木块样品，记录每个样本标号。

根据《木材密度测定方法》（GB/T 1933—2009）的标准，采用排水法对落叶松样品进行基本密度的测定。采用SPXY（sample set partitioning based on joint x-y distances）方法对120 个样品进行划分，将自变量与因变量相结合以选择具有代表性的样本，由K-S (Kennard-Stone)方法进一步发展而来[24]。样本集中2/3 为校正集，1/3 为验证集。测得的120 个落叶松样品基本密度在0.347 3 ～0.513 8 g∙cm-3之间，平均值为0.421 3 g∙cm-3，标准差为0.045 17 g∙cm-3（表1）。

开发绿色能源，实现绿色建设，是现阶段国家发展的重要战略目标。光伏发电，是一种可再生的绿色清洁能源，能有效缓解我国在经济建设中的能源匮乏问题［1］。简单来说，光伏发电就是将太阳能转化成电力，方便人们的生产生活。光伏发电与煤炭发电不同，光伏发电不会产生垃圾、有毒物，不会出现资源浪费，且是取之不尽，用之不竭的。而电气自动化能够有效提高太阳能利用效率，通过对电气自动化在太阳能光伏发电中的应用研究，解决我国在资源配置方面遇到的各种问题。

1.2 木材基本密度的测定

MS是一种罕见的发生于骨髓外的由未成熟髓细胞构成的局限性实体肿瘤，可发生于人体的任何部位，尤其是皮肤、淋巴结、软组织和骨骼等。MS可作为一种独立的肿瘤存在，但更常见于AML患者中，尤其是M4、M5和M2亚型。APL是一种以出血为主的特殊类型急性髓系白血病，髓外浸润也比较少见，且常累及中枢神经系统，其次是皮肤、耳道、鼻咽、睾丸和淋巴结等。至今以MS合并APL尤其是MS作为APL首发症状的病例报告较少，国内外也仅为个别病例报告（表 1）[3-13]。

表1 样品基本密度统计Table 1 Basic density statistics of the wood samples

1.3 样品近红外光谱的采集

不同表面粗糙度的近红外光谱图吸光度产生了差异，大体上呈现表面越粗糙其吸光度越高的趋势。砂纸目数越高，其表面打磨也越光滑。如图1 所示，在波长1 350 ～2 500 nm 之间，M2 的样品吸光度最低，M0 的样品吸光度最高，即样品Ra值越高，样品吸光度越高。在波长350～1 350 nm之间，M1 的吸光度仍高于M2 样品，而M0 的样品吸光度处于两者之间。落叶松样品近红外光谱采集方式是漫反射方式，样品表面越光滑，光的反射率越大；随着样品表面粗糙度的增加，光经过多次的反射、折射、衍射携带的相关信息会增加。因此，样品表面粗糙度对近红外光谱产生较大影响，进而影响近红外光谱分析技术的预测能力。

福建亚通新材料科技股份有限公司创建于1994年，是一家专业从事塑料管道产品研究和制造的国家级重点高新技术企业。亚通产品主要用于市政建设（道路、通信、电力、燃气、供水、排水、排污等基础设施建设）、水务投资运营（城市供水、排污、输水管网建设改造）、建筑工程、农业节水排灌系统、现代园艺等各种领域，产品种类及配套之全，位居全国同行业领先地位。

此时期是小麦病虫害防治的关键期，主要病害以小麦锈病和小麦纹枯病为主，虫害有蝼蛄、金针虫等。该时期病虫害较多，需加强对麦田的监测，防治措施以物理和化学防治相结合，如及时拔除杂草、针对性的喷洒农药等。

2 结果与分析

2.1 不同表面粗糙度的光谱分析

同一落叶松样品在M0、M1 以及M2 的条件下，表面粗糙度不同，其近红外光谱的线形图（图1）并无较大差异，且均在波长为1 415、1 892、2 056 nm 处出现了明显的吸收峰，与李耀翔等[25]的研究结果基本一致。

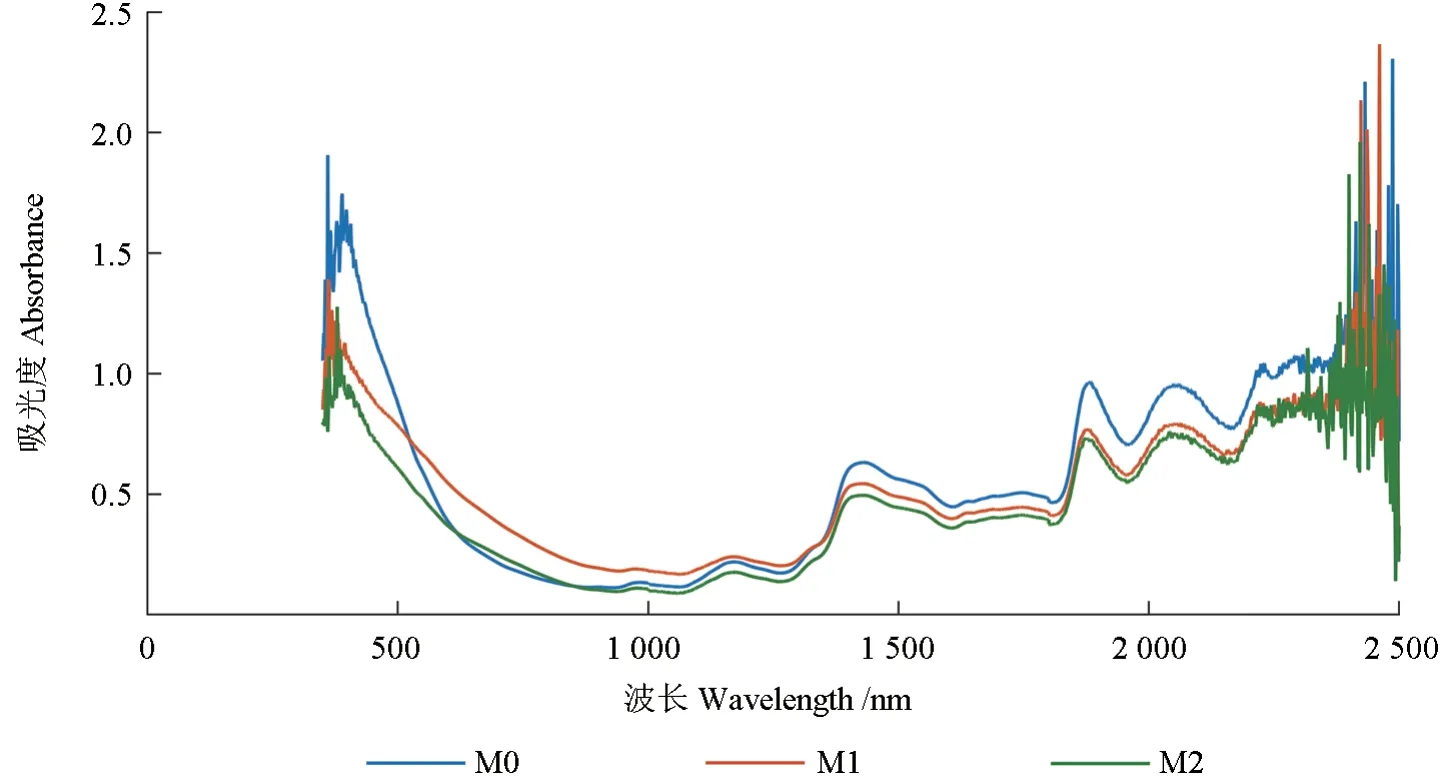
图1 不同表面粗糙度下的木材近红外光谱Fig. 1 NIR spectra of wood with different surface roughness

试验采用美国ASD 公司的LabSpec® Pro FR /A114260 便携式物质成分分析光谱仪测量近红外光谱。该仪器可选择的光谱范围为350 ～2 500 nm，光谱分辨率为3 nm @700 nm、10 nm@1 400 nm 和2 100 nm。光谱采样间隔为1.4 nm@350 ～1 050 nm、2 nm @1 000 ～2 500 nm。

尽管国际经济出现复苏，但全球性贸易仍然继续震荡，欧元区经济增速放缓，新兴市场经济动荡加剧，加上西方一些国家所设的各种经济壁垒，国际林产品市场竞争激烈，我国木材制品出口仍较困难。随着“一带一路”倡议的推进，深圳、成都、郑州等多个城市相继开通中欧班列，由于班列运输时间比海运缩短三分之二，价格是空运的四分之一，因而加速我国木材加工产品对“一带一路”沿线国家的出口速度，前3季度我国的刨花板和胶合板出口数量都实现了增长。纤维板的出口数量下降不少，但出口金额降幅收窄，木家具出口数量有增长，但出口金额基本与去年同期持平。

2.2 光谱预处理方法

近红外光谱在采集过程中容易携带无关噪声，对近红外光谱分析产生影响，因此需要对近红外光谱原始数据进行预处理，以此来获得具有高信噪比和低背景干扰的近红外信号。常见的预处理方法包括移动平均平滑、SG 平滑、导数处理、基线校正（baseline）、MSC、SNV 等方法。

通过对比实验得到的冲击端应力曲线和D-R-PH模型的结果，表明了利用该方法对于确定泡沫材料的动态参数具有较高的可行性和准确性。通过对比准静态实验的应力-应变曲线，可以从实验的角度得到不管泡沫铝是何种相对密度，它都是一种冲击速率相关的材料的结论。

为模拟木材在加工过程中其表面未加工、粗加工、精加工的情况，对含水率12%的落叶松样品设置3 种不同的表面粗糙度条件，分别为未打磨（M0）、150 目砂纸打磨（M1）、320 目砂纸打磨（M2）。以M0 样品作为对照组，在室温20 ℃、空气湿度50%条件下使用二分光纤探头对样品横截面两个不同位置进行光谱采集；之后以150 目砂纸对样品连续打磨30 次，打磨完后在相同条件下采集近红外光谱；完成150 目打磨后以320 目砂纸对样品连续打磨30 次，仍以相同方式采集光谱。在采集光谱过程中，设置采集次数为30 次，采集间隔为1 nm，每采集3 ～5 个样品，需要对准聚四氟乙烯标准白板进行校准。将得到的光谱数据导入到ViewSpec Pro 软件和The Unscrambler X 10.4 (64-bit) 软件中进行处理，涉及到的算法均在MATLAB R2017a 软件上操作。

从图1 可以看到，在350 nm 附近和2 500 nm附近包含大量噪声等无用信息，为提高建模精度和速度，选择波段600 ～2 200 nm 这部分光谱进行后续的处理和建模。本研究主要讨论11 点移动平均平滑、SG 平滑和基线校正这3 种预处理方法对预测模型的影响。不同表面粗糙度的样品使用不同光谱预处理的效果如表2 所示。M0 的样品使用原始光谱建立的回归模型的校正集相关系数（Rc）为0.882 3，校正集均方根误差（RMSEC）为0.020 7，验证集相关系数（Rp）为0.854 8，RMSEP为0.023 6。采用11 点平滑、基线校正及SG 平滑进行预处理的光谱建立的回归模型，其Rc均低于原始光谱，11 点平滑和SG 平滑预处理的Rp均高于原始光谱，11 点平滑的RMSEP为0.023 4，SG 平滑的RMSEP为0.023 5。

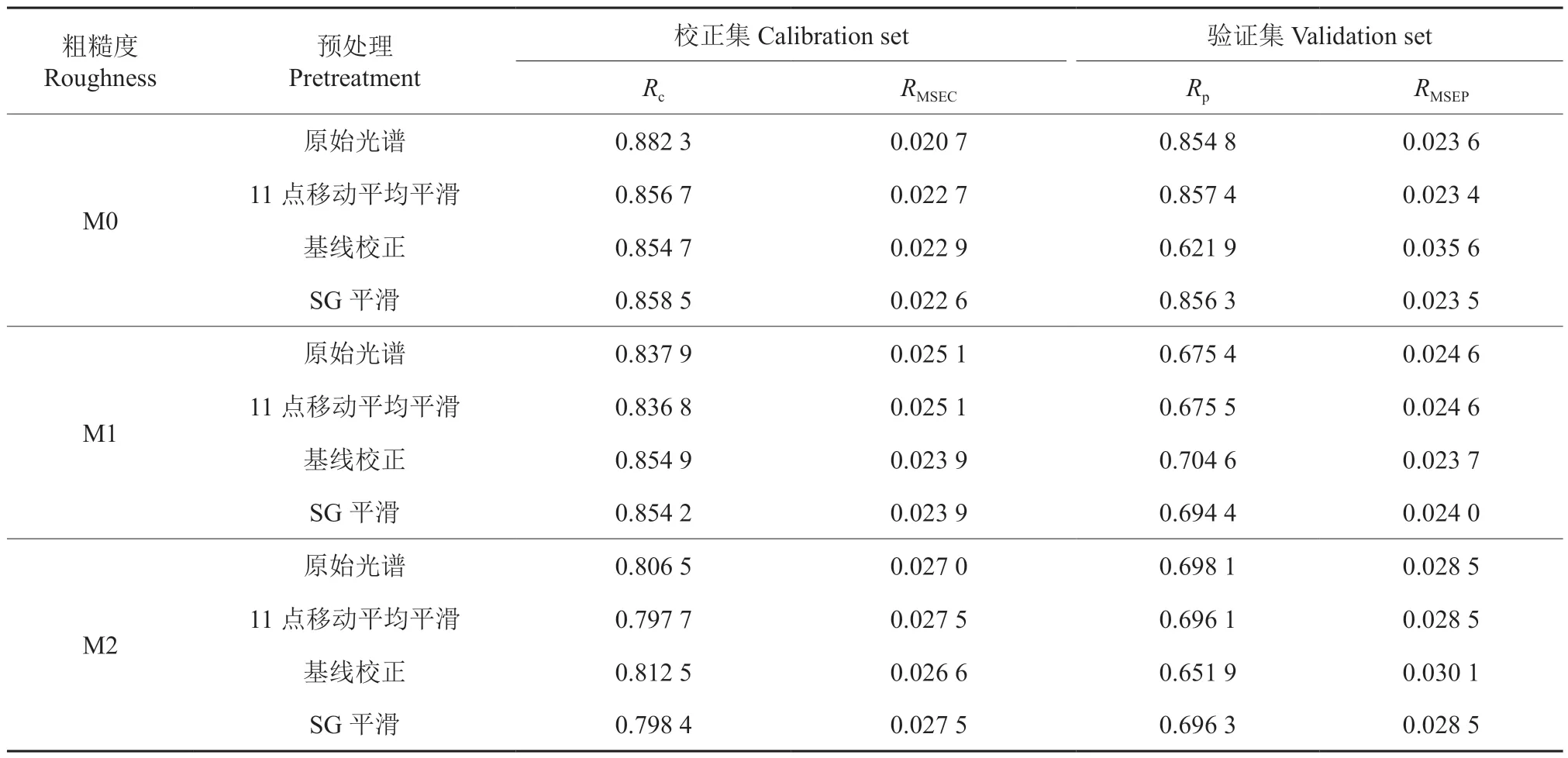
表2 基于不同预处理的不同表面粗糙度落叶松基本密度预测模型Table 2 Prediction models for basic density of larch based on different pretreatments of different surface roughness samples

M1 的样品采用原始光谱建立的回归模型的Rc为0.837 9，RMSEC为0.025 1，Rp为0.675 4，RMSEP为0.024 6。在3 种预处理方法中，11 点平滑处理的效果较差，校正集与验证集的结果都不理想，基线校正与SG 平滑的Rc和Rp都好于原始光谱，RMSEP分别为0.023 7 和0.024 0。

BiPLS 是在iPLS 基础之上提出的特征波段选择方法，其将整个光谱区划分为若干个等宽的区间，之后基于全光谱建立回归模型。以交叉验证均方根误差RMSECV为评价指标，每次剔除一个区间，以剔除后剩下的区间为基础建立PLS 模型，以此反复直至剩下最后一个区间，然后以RMSECV最小的区间组合作为特征波段建立PLS 回归模型。

M2 的样品采用原始光谱方法建立的模型效果最好，优于其他预处理方法，Rc为0.806 5，RMSEC为0.027 0，Rp为0.698 1，RMSEP为0.028 5。采用11 点平滑和SG 平滑处理的光谱建立的验证模型相关系数为0.696 1 和0.696 3，均略低于原始光谱的Rp，RMSEP均为0.028 5。

“柳哥人才可惜了啊。”寝室二床说道，“柳哥这成绩，出国拿全奖，毕业美利坚啊！”当然，这都是大学寝室里没有任何恶意、近乎习惯的互捧。

在表面粗糙度不同的条件下，各个预处理方法对回归模型的预测能力产生的效果各不一样。针对M0 样品SG 平滑的预处理效果与11 点平滑法差别不大；M1 样品中SG 平滑的预处理效果略逊于基线校正，优于其他方法；M2 样品中3 种预处理方法对预测模型均无较大改善，预处理的效果与原始光谱相差不大，其中 SG 平滑预处理表现较好。综合考虑，采用SG 平滑建模的效果略好于原始光谱、11 点平滑、基线校正这3 种预处理方法，因此，采用SG 平滑预处理后的光谱进行接下来的波段选择和建模。

2.3 特征波段选择方法

近红外光谱数据通常包含成百上千个数据点，在建立近红外光谱模型时全光谱数据一般携带大量冗余信息，从而影响建模的速度和准确性。为了减少大量重叠的无用信息对多元校正模型的干扰，对原始全波段光谱数据进行选择，筛选出共线性少、冗余信息少且包含主要有效信息的波段。目前应用较为广泛的特征波段选择方法包括间隔偏最小二乘法（iPLS）、反向区间偏最小二乘法（BiPLS）、联合区间偏最小二乘法（SiPLS）和移动窗口偏最小二乘法（MWPLS）等。

实验组患者中有1例患者唾液增多,有1例患者失眠,不良反应发生率为12.5%;对照组患者中有1例患者唾液增多,有2例患者心动过速,有1例患者嗜睡,不良反应发生率为25.0%。实验组明显低于对照组,两组差异对比具有统计学意义,P<0.05。

SiPLS 方法在均匀划分的m个等宽区间中随机选取n个区间组成联合区间并建立PLS 模型，这种方法弥补了iPLS 单一区间容易造成光谱信息遗漏的缺点，比较不同模型的效果，选择其中RMSECV最小的联合区间作为特征波段。由于SiPLS的计算量比较大，通常区间n的数量不超过5 个。

采用BiPLS 方法进行波段选择，为了减少区间数量对预测结果的影响，将全光谱数据划分为20 ～40 个区间，优选出RMSECV值最小的区间数。当区间数为36 时，M0 样品的RMSECV值最小为0.026 7，选取了220 个特征波长点，对应的波段为1 629 ～1 716、1 849 ～1 892、2 025 ～2 068、2 113 ～2 156 nm（图2a）；当区间数为38 时，M1 样品的RMSECV值最小为0.023 4，选取了464 个特征波长点，对应的波段为600 ～642、772 ～856、983 ～1 108、1 277 ～1 318、1 613 ～1 654、1 865 ～1 906、2 117 ～2 200 nm（图3a）；当区间数为29 时，M2 样品的RMSECV值最小为0.025 9，选取了663 个特征波长点，对应的波段为600 ～655、768 ～823、880 ～990、1 101 ～1 210、1 321 ～1 430、1 541 ～1 595、1 926 ～2 090 nm（图4a）。

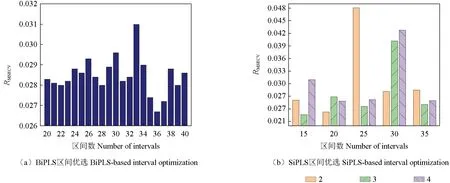
图2 M0 样品波段区间优选Fig. 2 Band interval optimization of the M0 sample

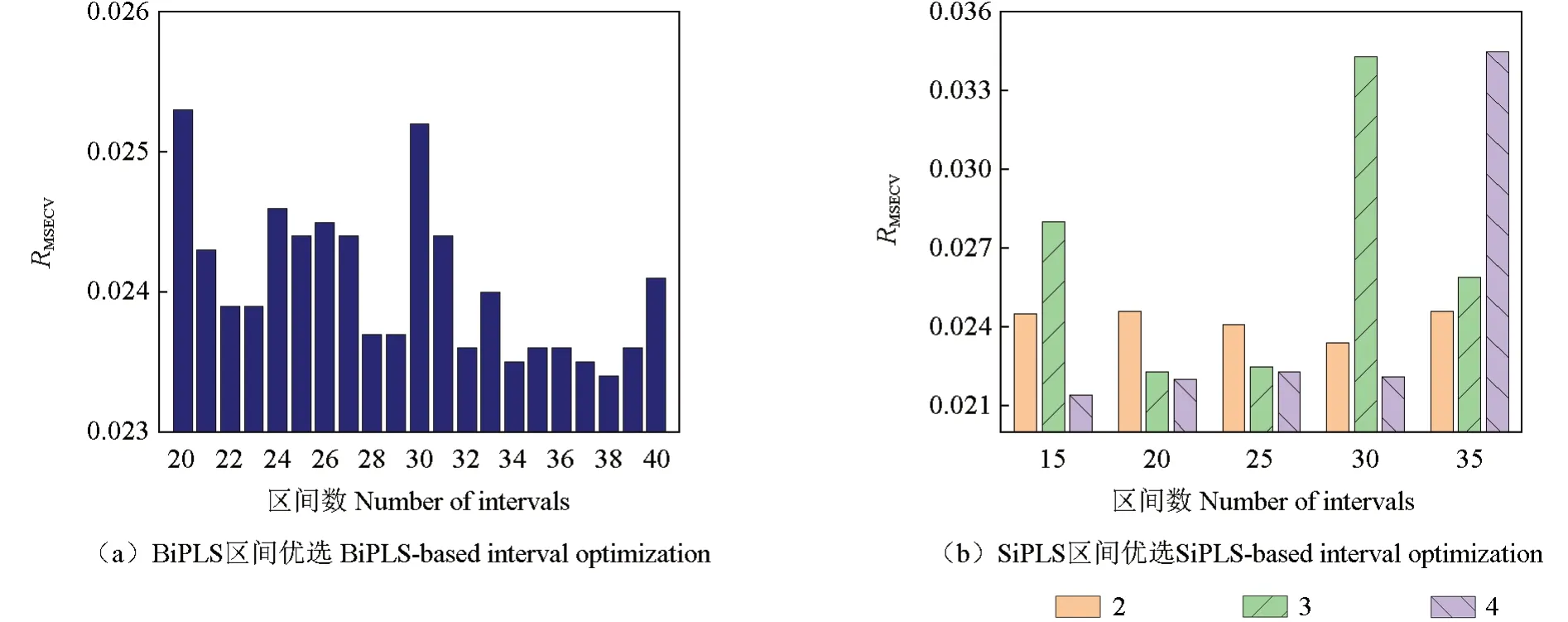
图3 M1 样品波段区间优选Fig. 3 Band interval optimization of the M1 sample

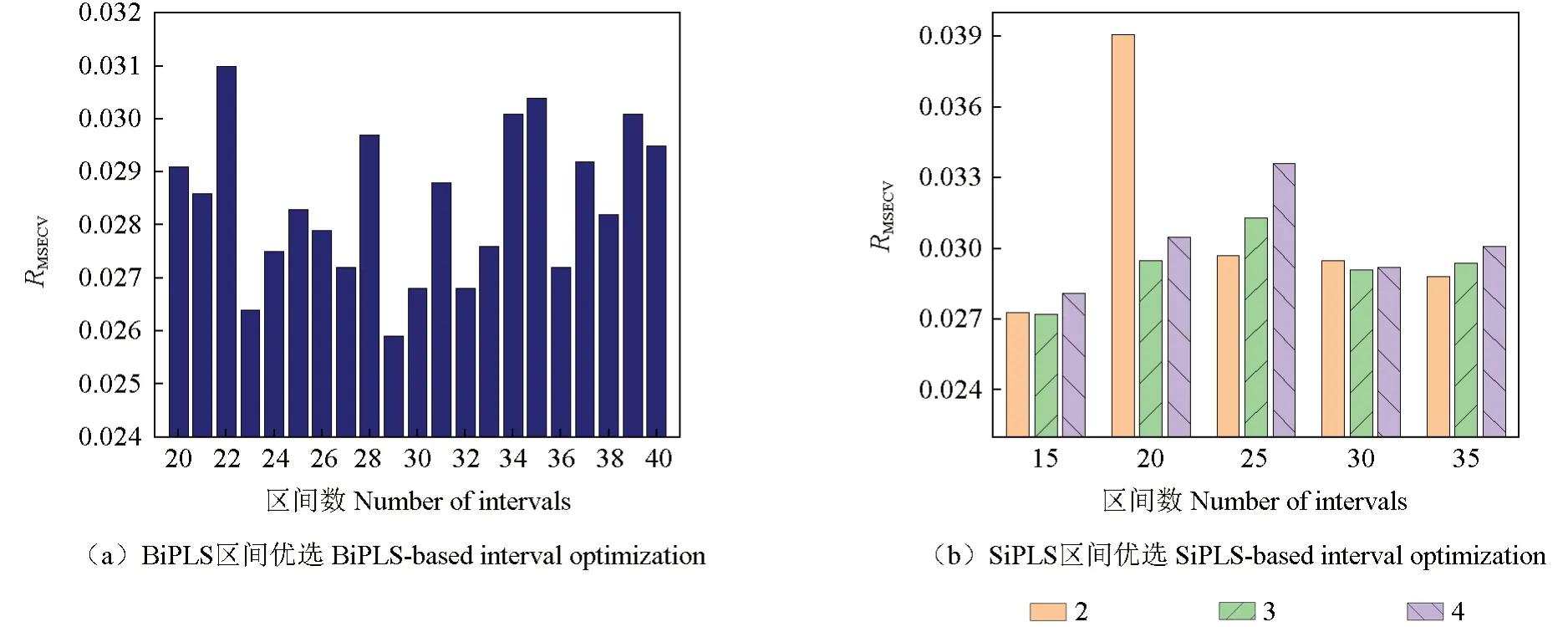
图4 M2 样品波段区间优选Fig. 4 Band interval optimization of the M2 sample

采用SiPLS 方法进行波段选择，将全光谱数据分别划分为15、20、25、30 和35 共5 个区间数，并且在区间内分别选择2、3、4 个区间进行组合，同样优选出RMSECV值最小的区间组合。当区间数为20、组合区间数为3 时，M0 样品的RMSECV值最小为0.022 7，选取波段为1 135 ～1 348、1 670 ～1 776 nm（图2b）；当区间数为15、组合区间数为4 时，M1 样品的RMSECV值最小为0.021 4，选取波段为707 ～920、1 242 ～1 348、1 456 ～1 562 nm（图3b）；当区间数为15、组合区间数为3 时，M2 样品的RMSECV值最小为0.027 2，选取波段为1 028 ～1 134、1 883 ～2 094 nm（图4b）。

2.4 落叶松木材密度近红外模型的构建

2.4.1 基于不同粗糙度的近红外模型

在不同表面粗糙度下，以人工选择的波段、BiPLS 和SiPLS 选择的波段分别建立预测模型。如表3 所示，与人工选择波段和BiPLS 相比，M0 和M1 采用SiPLS 选取的特征波段建立的PLS 回归模型效果最好，M0的Rp为0.865 9，RMSEP为0.022 7，主因子数为7；M1 的Rp为0.766 0，RMSEP为0.021 4，主因子数为9；BiPLS 波段选择方法对M0 的建模效果不如人工选取的波段。M2 样品是采用BiPLS选取的特征波段建立的PLS 回归模型效果最好，主因子数为7，Rp为0.756 5，RMSEP为0.026 0；采用SiPLS 选取的特征波段建立的模型效果次之，主因子数为5，Rp为0.725 6，RMSEP为0.027 4。由表3 可知，采用SiPLS 方法选择的特征波段数小于BiPLS 和人工选择，表明SiPLS 方法在选择特征波段时去掉了大量的无用噪声，尽可能地保留有用的光谱信息。综合在不同表面粗糙度条件下的建模表现效果，SiPLS 建模方法是这3 种方法中稳定性和准确性最好的方法，并且随着从M0、M1、M2 样品粗糙度的降低，预测模型的精度也变低，M0、M1、M2 的Rp分别为0.865 9、0.766 0、0.725 6。

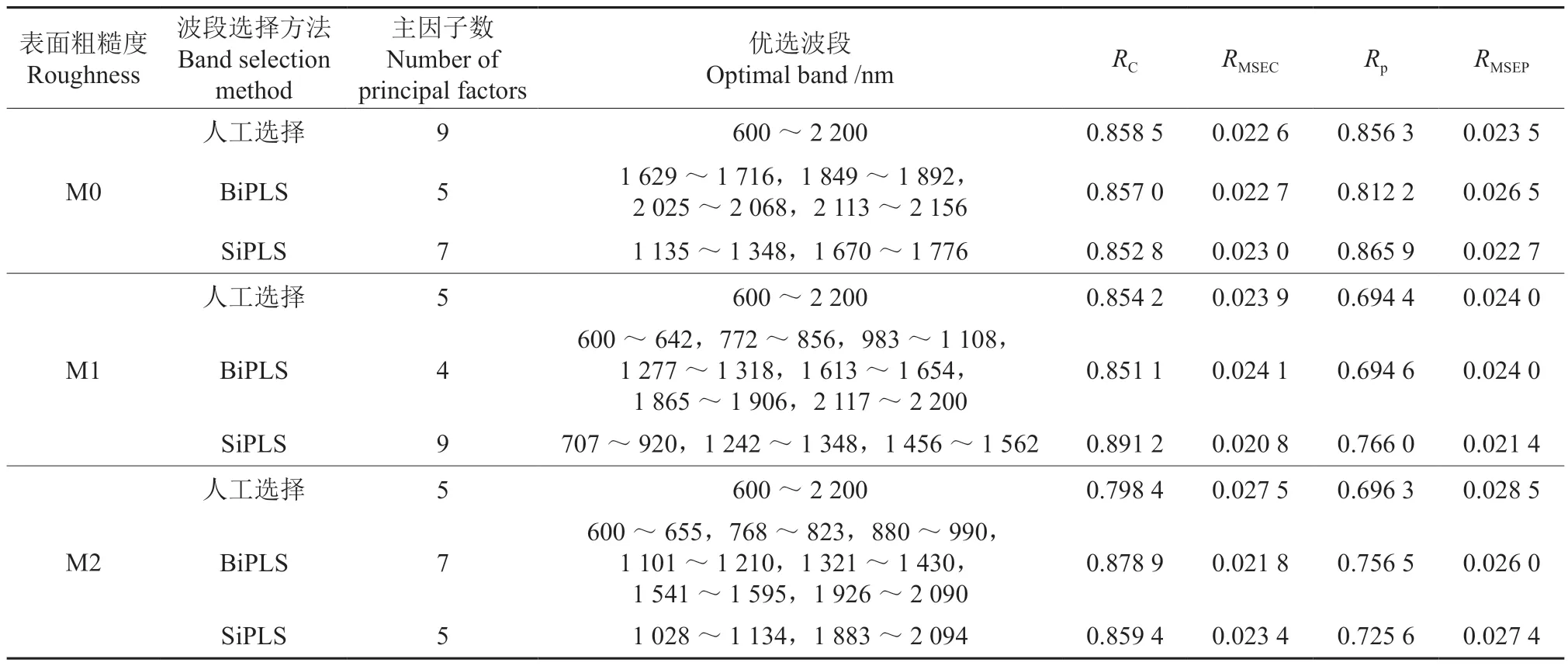
表3 不同波段选择方法对不同粗糙度样品的建模结果Table 3 Modeling results of different waveband selection methods for samples with different roughness

2.4.2 基于3 种粗糙度混合样本的近红外模型

为了减少样品表面粗糙度对落叶松样品基本密度预测的影响，利用包含M0、M1 以及M2 的样品建立混合校正模型，并且依旧采取上文的SPXY 样本集划分方法（校正集为240 个样本）。采用SiPLS 波段选择方法选择合适的波段，建立PLS 回归模型。

从样品前期处理过程(1.3.1)的步骤来看，可能引入的干扰元素来自两方面。一方面，在车床上对高纯锡样品的表面刨光处理时，由于接触样品分析面的车刀是钢材质的，因此在该过程可能会对样品分析面引入Fe元素的污染；另一方面，后续样品的清洗过程中所使用的硝酸和超纯水，可能会残留一些离子污染样品分析面，对分析有直接影响的就是Ca、Mg离子。只要通过预溅射使这3种可能存在的干扰元素含量趋于平稳，即可正常检测采集数据组。

当区间数为20、联合区间数为4 时，选取的结果最优，入选区间为8、10、12、13 这4 个区间，对应的波段为1 106 ～1 213、1 322 ～1 429 和1 538 ～1 751 nm（表4）。从每种粗糙度中选取40 个样品，分别验证每种粗糙度的预测能力。如表5 所示，M0 样品的RMSEP从0.022 7 降低到了0.020 1，M1样品的RMSEP从0.021 4降低到了0.016 0，M2 样品的RMSEP从0.027 4 降低到了0.026 1，表明SiPLS 选择的波段范围包含了M0、M1 和M2 这3 种粗糙度的重要信息，基于此建立混合模型的预测能力要好于单一模型，在波段范围1 106 ～1 213、1 322 ～1 429 和1 538 ～1 751 nm建立的模型可以有效降低样品表面粗糙度的影响，提高了模型的稳健性。

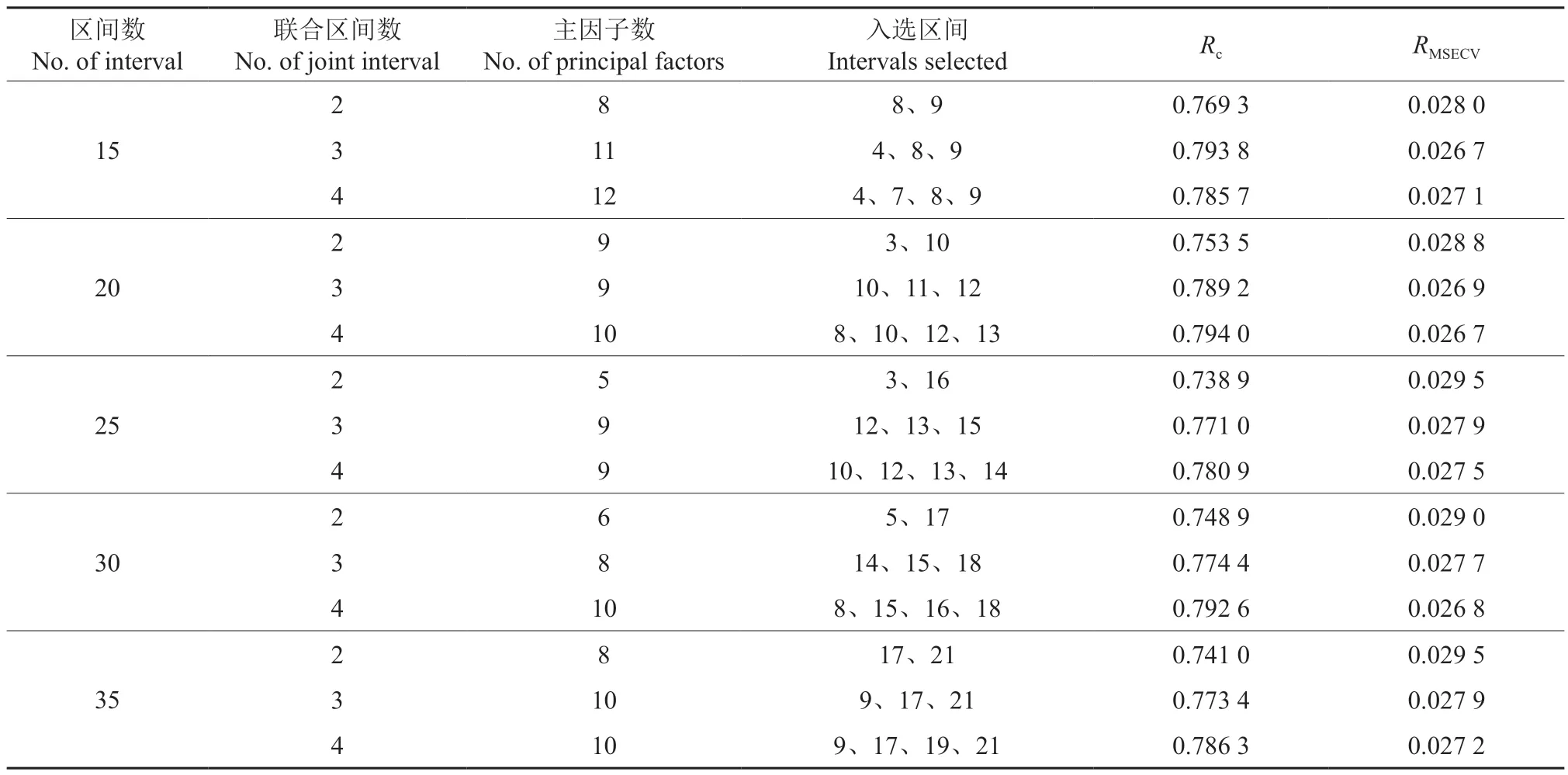
表4 不同区间数下SiPLS 混合模型波段优选Table 4 Band selection of the SiPLS mixed model under different interval numbers

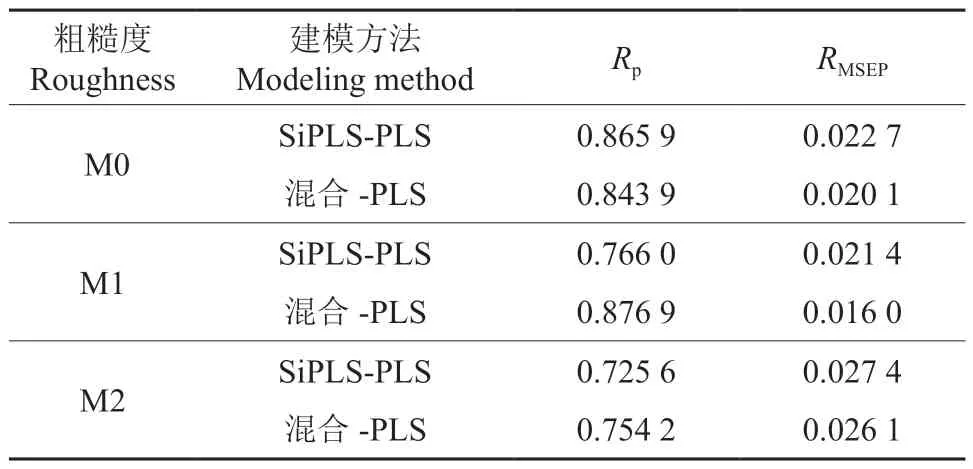
表5 混合模型预测不同粗糙度结果Table 5 The prediction results of the mixed model for samples with different roughness

3 结论与讨论

3.1 结 论

本文研究了表面粗糙度为未打磨（M0）、150目（M1）和320 目（M2）打磨的样品对基于近红外技术预测落叶松基本密度的影响。讨论不同粗糙度样品光谱产生的差异，对比分析在人工选择波段、BiPLS 和SiPLS 波段优选方法下，构建预测落叶松样品基本密度模型的效果，在此基础上建立混合模型减小粗糙度的影响，提高预测精度。

研究表明，在不同表面粗糙度条件下，样品表面越粗糙，样品光谱的吸光度越高（M0 ＞M1 ＞M2），表面粗糙的样品携带的光谱有效信息要多于表面光滑的样品。在不同波段优选方法中，针对不同表面粗糙度的样品，SiPLS 优选出的特征波长点包含更多的有效信息，与其他波段选择方法相比其具有更大的优势。基于SiPLS 和PLS 建立的回归模型准确性更高，表明经过SiPLS波段优选可以有效降低不同表面粗糙度对NIR 预测模型的影响。所建模型对不同粗糙度的预测结果为M0＞M1＞M2，呈现出与粗糙度相同的趋势，表明粗糙度的程度与预测结果精度存在一定联系。混合模型经SiPLS 优选的波段范围为1 106 ～1 213、1 322 ～1 429 和1 538 ～1 751 nm，表明在此区间内包含了不同粗糙度样品的光谱信息。采用不同粗糙度样品建立的SiPLS-混合模型效果要好于不同粗糙度的单一模型，RMSEP均得到了不同程度的提高，表明建立混合模型可以有效提高近红外模型的稳健性与普适性。

3.2 讨 论

木材种类繁多，通常将其分为针叶材和阔叶材两大类，根据各自的特性不同，在木材工业上的用途也不一样。在木材工业中，利用近红外技术对木材的物理力学性质等进行预测时，由于加工方式不同，表面粗糙度的影响是不可避免。

本研究主要针对的是东北地区的落叶松木材，分析其不同表面粗糙度对NIR 预测模型的影响，研究结果是否适用于其他种类的针叶材或阔叶材有待进一步验证。在实际的应用中NIR 会受到多种因素的影响，不仅是表面粗糙度，还包括温度、含水率和操作者因素等，优化影响因素的方法也各不相同。在后续的研究中对其他针叶材和阔叶材进行不同表面粗糙度的处理，验证表面粗糙度对NIR 预测木材密度的影响，提出适用于大部分木材的优化方法，建立适用范围更广的NIR 预测模型。为了进一步提高模型的普适性，近红外检测技术及模型传递方法的结合可能会成为木材生产加工领域新的应用方向，这也将是下一步研究的重点。