基于红外光谱的SSA-ELM石墨烯成分含量预测分析

吴宇强 董宇欣

摘 要：为提高石墨烯成分含量软测量精度，提出一种基于红外光谱的SSA-ELM的石墨烯成分含量预测算法。针对ELM模型预测性能受其初始权值和阈值的影响，运用SSA算法对ELM模型的初始权值和阈值进行优化选择。将石墨烯材料的红外光谱吸光度作为ELM的输入，石墨烯含量作为ELM的输出，建立红外光谱的石墨烯成分含量预测模型。试验分析表明，与GA-ELM、PSO-ELM、 ELM等方法比较，使用SSA-ELM的石墨烯成分含量预测模型的预测精度最高，为石墨烯成分含量软测量提供了新的方法。

关键词：红外光谱；樽海鞘群算法；极限学习机；石墨烯；软测量

中图分类号：TP391；TQ327.6

文献标志码：A文章编号：1001-5922（2023）04-0114-04

Prediction and analysis of SSA-ELM graphene component content based on infrared spectroscopy

WU Yuqiang，DONG Yuxin

（Yanan University，Yanan 716000，Shaanxi China）

Abstract：In order to improve the soft measurement accuracy of graphene content，an algorithm for graphene content prediction based on infrared spectrum was proposed.According to the influence of the initial weight and threshold of ELM model，the SSA algorithm wasused to optimize the initial weight and threshold of ELM model.The prediction model of graphene content in infrared spectrum was established，using the infrared spectroscopic absorption of graphene material as the input of ELM，and the graphene content as the output of ELM.The results show that compared with GA-ELM，PSO-ELM and ELM，SSA-ELM has the highest accuracy in predicting graphene content，providing a new method for soft measurement of graphene content.

Key words：infrared spectrum;salp swarm algorithm;extreme learning machine;graphene;soft measurement

石墨烯自被发现以来，因为优异的力学性能和良好的导电性能被认为是理想的铜基复合材料增强体。目前世界上最高强度和最硬的材料于一体的是石墨烯，这种材料的抗拉强度是125 GPa，弹性模量也达到了1.1 TPa，强度极限为42 N/m2；同时，在室温条件下，石墨烯是最优异的导电材料［1］。因此，在铜基复合材料中加入适量的石墨烯不仅能使其具有良好的导电性能，还能增强其力学性能。

目前被广泛地应用于工业领域的基于数据驱动的软测量方法中技术最成熟的是神经网络技术。神经网络技术中的极限学习机（ELM）属于单层的前馈神经网络算法，其典型优势是训练的速度非常快，具有训练速度快、复杂度低的优点，目前被广泛地应用于模式识别、故障诊断、机器学习、软测量等领域。然而由于参数的起始值以及隐含层偏执选择会极大的影响ELM模型的性能，本文重点对ELM模型的参数初始值进行了有针对性的优化基础上，提出了樽海鞘群算法（SSA），该算法也改善了隐含层偏置值，并將SSA-ELM应用红外光谱的石墨烯成分含量预测研究。试验结果表明，与GA-ELM、PSO-ELM、 ELM等方法比较，使用SSA-ELM的石墨烯成分含量预测模型的预测精度最高，这为石墨烯成分含量软测量提供了新的方法。

1 试验仪器

ASD光谱仪波长范围为400～2 500 nm，波长精度为±1 nm，主要由连接探头、主机箱和笔记本电脑组成。

2 樽海鞘群算法

2.1 初始化种群

自然界中的樽海鞘捕食属于一种群体行为，受该行为的启示Seyedali等学者提出了SSA算法［2］，在算法中假设了具有N个种群的樽海鞘的捕食搜索空间将达到N×D维，其中D代表了优化问题的维度。为了获得樽海鞘种群的初始化结果，学者们提出了初始化公式：

XN×D=rand（N，D）×（ub－lb）+lb（1）

在式（1）中，首先定义F=［F1，F2，…，FD］T代表搜索空间的食物;同时，使用X=［Xn1，Xn2，…，XnD］T标记樽海鞘的活动坐标，并定义了樽海鞘活动空间的上限值［ub1，ub2，…，ubD］T和下限值lb=［lb1，lb2，…，lbD］T。且由于樽海鞘是群体活动的一部分，需要区分领导维和普通追随者维，使用值X1d和Xmd，分别指代，并使用d=1，2，3，…，D表征领导维数编号并使用m=2，3，…，N指导普通追随者的代码。

2.2 领导者位置更新

在樽海鞘群体捕食策略中，领导者负责引领整个群里来找到食物，映射到SSA算法中，其核心在于领导者的定位并随机更新位置的策略要求比较高，其更新策略：

X1d=Fd+c1（（ubd－lbd）c2+lbd，c30.5Fd－c1（（ubd－lbd）c2+lbd，c3<0.5（2）

式中：c2、c3为控制参数，c2、c3∈［0，1］的随机数，主要为了加强领导者位置更新的个体多样性、随机性以及SSA算法的全局搜索能力。

c1为收敛因子：

c1=2e－（4t/T）2（3）

式中：t為当前循环参数值；T为整个循环的次数。

2.3 更新追随者位置

从文献［3］中可以看出，追随的位置仅与初始位置、速度和加速度相关。其更新公式：

R=12（Xm－1d-Xmd）（4）

Xm'd=Xmd+R=12（Xmd+Xm－1d）（5）

式中：R为运动距离；Xm'd、Xmd分别为第 m个跟随者第 d维度的位置和更新后的位置。

3 利用SSA-ELM法进行石墨组分的计算

3.1 极限学习机

与常规神经网路比较， ELM的特点是训练时间短，运算更容易，且其模型的构造如图1所示。

使用（Xi，Ti）表示训练样本，对于N个训练样本而言，将Xi=［xi1，xi2，…，xin］T∈Rn表征为输入值，对于训练样本值Ti=［ti1，ti2，…，tin］T∈Rm代表为目标向量，X、T是 n ×Q、m ×Q的矩阵， Q是训练样本量。由此， ELM的输出可以由具有 L的隐含层神经元数目来表达［5］：

∑Li=1βig（Wi·Xj+bi）=oj，j=1，2，...，N（6）

式中：Wi=［wi1，wi2，…，win］T为输入权重；βi为输出权重；bi为第i个隐含层节点的偏置；g（x）为激励函数；Wi·Xj为Wi和Xj的内积。ELM模式的学习目的是将式（7）中的错误减至最少［6］：

∑Nj=1‖oj－tj‖=0，j=1，2，...，N（7）

由式（6）和式（7）可知，即存在一组参数βi、Wi和bi使得式（8）成立：

∑Li=1βig（Wi·Xj+bi）=tj，j=1，2，...，N（8）

式（8）的矩阵形式为［7］：

Hβ=T（9）

式中：H、β分别为隐含层神经元的输出和输出加权。

用式（9）可以获得输出层权重矩阵中的最小二乘解的估算β^：

minβ‖T－βTH‖22（10）

β^=HHT－1HHT（11）

3.2 适应度函数

基于传统 SSA的方法，提出了一种基于SSA的方法的权值Wi以及隐含层偏置bi提高为了ELM模型的预测的准确率，对ELM模型的初始输入权值Wi和隐含层偏置bi进行优化选择，在 ELM模型中，以平均偏差为最小时，最优的参数是初始输入权重 Wi和隐含层偏差bi：

minf（Wi，bi）=1n∑ni=1（x（i）－xpred（i））2

s.t.Wi∈［Wimin，Wimax］ bi∈［bimin，bimax］（12）

式中：n为训练样本数量；x（i）、xpred（i）分别为 i个样品的真实数值和预计数值；［Wimin，Wimax］与［bimin，bimax］分别为ELM模式的第1个初始输出权重 W和第 i个隐藏层偏差 b的上限，且W∈［-1，1］和b∈［-1，1］。

3.3 算法步骤

为实现石墨烯成分含量预测，基于红外光谱的石墨烯成分含量SSA-ELM预测模型的算法步骤可描述为：

第1步，输入数据初始化（石墨烯光谱数据和含量数据）。输入数据并读取输入的结果，完成归一化的数据预处理，并对输入数据按照4∶1的比率分割为训练数据集合测试数据集；

第2步，参数初始化。主要是对SSA算法中的樽海鞘的种群规模N设置初始值，同时定义循环次数T，代入式（1）中获得樽海鞘种群，其中领导者活动的上下限值使用ELM获得；

第3步，获得训练集的樽海鞘整体适应值。主要是对训练集应用ELM模型算法后应用式（12）获取值；

第4步，根据樽海鞘的整体适应值结果，识别领导者和追随者以及相应的食物，将个体适应度按等级进行排序，确定最适合的樽海鞘作为当前的食物；其余N-1号的樽海鞘，将以第1位的樽海鞘为首，其余的则是追随者；

第5步，按式（2）和式（5）更新SSA算法的领导者位置和追随者位置；

第6步，对于新的樽海鞘群里使用式（12）计算适应度。并将其中的每个个体的适应度与对应的食物的适应度之差，如果差值大于0，则对应选择新的樽海鞘替换原樽海鞘位置值；

第7步，重复执行步骤3～步骤6，当达到t>T的临界值时，得到最佳食物位置，利用 ELM的最小初值和最大的内含层偏移，将最小的初值和最大的内含层偏差引入到 ELM中。利用 IR技术对SSA-ELM进行了石墨组分的计算。

4 实证分析

4.1 数据预处理

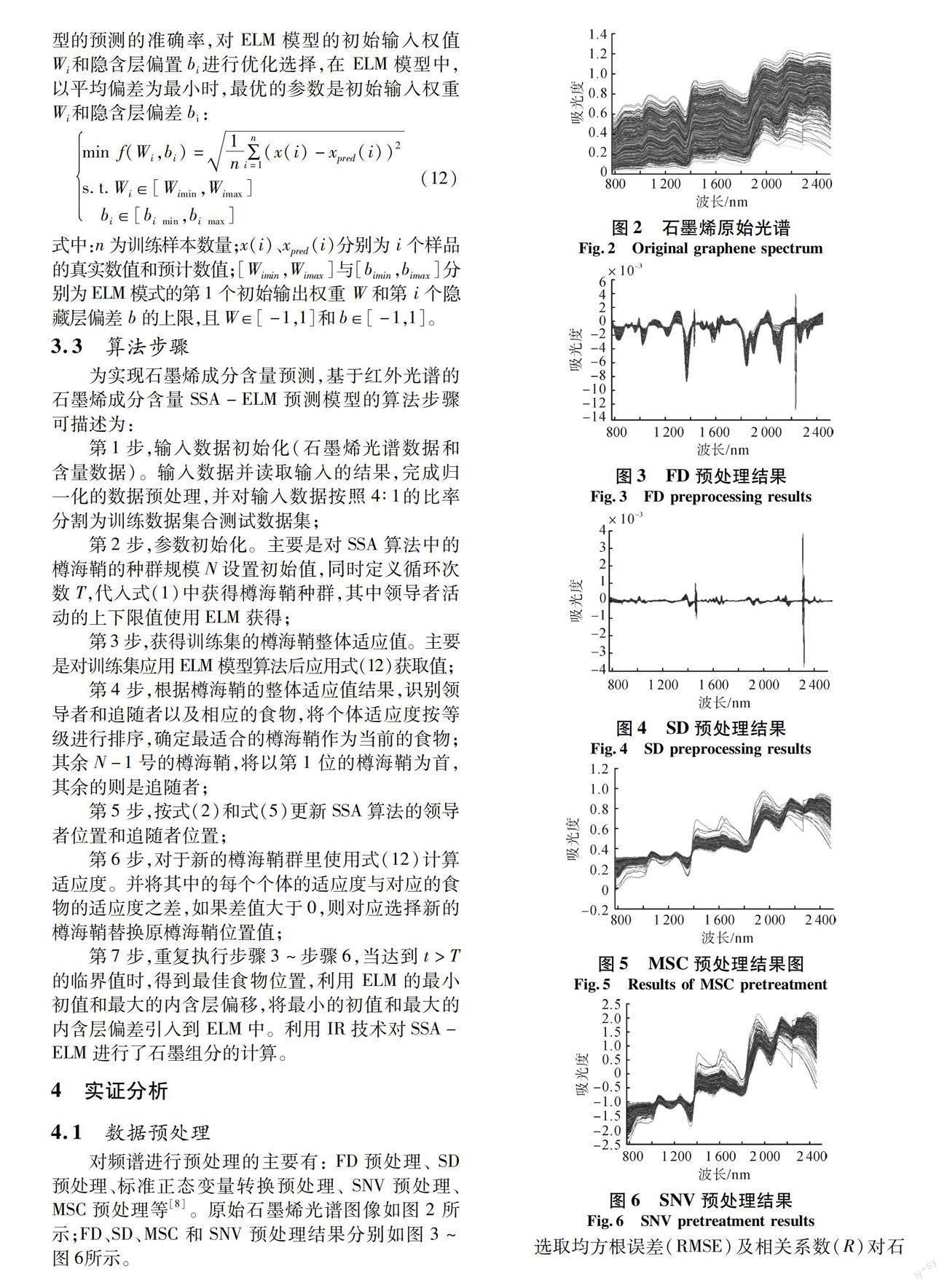
对频谱进行预处理的主要有： FD预处理、 SD预处理、标准正态变量转换预处理、 SNV预处理、 MSC预处理等［8］。原始石墨烯光谱图像如图2所示；FD、SD、MSC和SNV预处理结果分别如图3～图6所示。

选取均方根误差（RMSE）及相关系数（R）对石墨烯组分含量的预报特性进行评估 ［9-10］：

RMSE=1n∑nk=1（xk－predk）2（13）

R=∑nk=1xkpredk∑nk=1x2k∑nk=1pred2k（14）

式中：xk和predk分别为第k个样本的石墨烯成分含量实际值和石墨烯成分含量预测值；n为样本数量；RMSE用来评价石墨烯成分含量预测模型的离散程度；R用来说明石墨烯成分含量预测值和石墨烯成分含量实际值的关联程度，R的数值越接近于1，则说明石墨烯成分含量预测值和石墨烯成分含量实际值的关联程度越高，预测效果越好。

4.2 结果与分析

通过与GA-ELM、PSO-ELM、 ELM、 ELM、 ELM等方法进行对比，确定了SSA-ELM在石墨烯组分中的有效性和可靠性：（1）SSA算法：樽海鞘群体数量N=10，迭代次数 T=100。（2）遗传算法［11］（GA）算法：最大迭代次数T=100，种群规模N=10，變异概率pm=0.1，交叉概率pc=0.7。（3）粒子群算法［12］：学习因子c1=c2=2，最大迭代次数T=100，种群规模N=10，惯性权重w=0.8。（4）ELM模型［13-14］：输入层神经元数量N1=2 740、隐含层神经元数量N2=10以及输出层神经元数量为N3=1，本文收集了34个光谱数据，其中25个样本被用来作为训练样本，9个样本被用来进行实验。

从图7与表1石墨烯成分含量结果对比可知：

（1）通过石墨烯的含量在训练集和测试集的结果对比发现，对比GA-ELM，SSA-ELM

模型的石墨烯成分预测值更加精准。利用PSO-ELM、 ELM等方法对石墨烯组分进行了预测，其中，SSA-ELM模式的石墨烯组分含量预测指数 RMSE最小，相关系数R为最大，因此，SSA-ELM模式的石墨烯组分含量与石墨烯组分的真实值之间的关联度最大；

（2）利用 SSA、 GA、 PSO等方法，对 ELM模型进行初值和隐含层偏移的最优选取，

结果表明，利用SSA-ELM、GA-ELM和PSO-ELM模型具有更好的预测准确率。

5 结语

为了改善石墨烯组份的软化测定准确性，采用SSA-ELM技术建立了一种用于石墨烯组分含量的快速估算方法。针对ELM模型预测性能受其初始权值和阈值的影响，运用SSA算法对ELM模型的初始权值和阈值进行优化选择。将石墨烯材料的红外光谱吸光度作为ELM的输入，石墨烯含量作为ELM的输出，建立红外光谱的石墨烯成分含量预测模型。试验结果表明，与GA-ELM、PSO-ELM、 ELM等方法比较，使用SSA-ELM的石墨烯成分含量预测模型的预测精度最高，为石墨烯成分含量软测量提供了新的方法。

【参考文献】

［1］刘朋，闫翠霞，凌自成，等.石墨烯含量对铜基石墨烯复合材料力学和电学性能的影响［J］.材料导报，2017（S1）：295-300.

［2］ 田晓鸿.石墨烯制备及其在新能源汽车锂离子电池负极材料中的应用［J］.粘接，2021，45（1）：183-186.

［3］ IBRAHIM A，AHMED A，HUSSEIN S，et al.Fish Image Segmentation Using Salp Swarm Algorithm［C］// International Conference on Advanced Machine Learning Technologies & Applications.Springer，Cham，2018.

［4］ 余刚，汪洪.基于遗传算法的浮法玻璃光学常数测量与分析［J］.硅酸盐通报，2017（4）： 1107-1112.

［5］ 张东娟，丁煜函，刘国海，等.基于改进极限学习机的软测量建模方法［J］.计算机工程与应用，2012，48（20）：51-54.

［6］ 严东，汤健，赵立杰.基于特征提取和极限学习机的软测量方法［J］.控制工程，2013（1）：55-58.

［7］ 潘孝礼，肖冬，常玉清，等.基于极限学习机的软测量建模方法研究［J］.计量学报，2009，30（4）：324-327.

［8］ 吴德会.一种基于近红外光谱技术的柴油在线软测量方法研究［J］.光谱学与光谱分析，2008，28（7）：1530-1534.

［9］ 董学锋，戴连奎，黄承伟.结合PLS-DA与SVM的近红外光谱软测量方法［J］.浙江大学学报（工学版），2012，46（5）：824-829.

［10］ 贺凯迅，曹鹏飞.基于智能优化算法的软测量模型建模样本优选及应用［J］.化工进展，2018，37（7）：67-74.

［11］ 汤健，乔俊飞，柴天佑，等.基于虚拟样本生成技术的多组分机械信号建模［J］.自动化学报，2018，44（9）：35-55.

［12］ 张春晓，张涛.基于最小二乘支持向量机和粒子群算法的两相流含油率软测量方法［J］.中国电机工程学报，2010，30（2）：86-91.

［13］ 房慧，孙玉坤，嵇小辅.青霉素发酵过程的粒子群模糊神经网络软测量［J］.自动化仪表，2011，32（5）：46-48.

［14］ 陈如清，俞金寿.基于带扰动项粒子群算法的软测量建模［J］.华东理工大学学报，2007，33（3）：414-418.