基于非对称互注入WRC-FPLDs的波长可调谐的混沌同步

自2005年基于希腊雅典城域网首次实现混沌保密通信现场实验以来, 混沌保密通信引起了人们越来越多的关注[1]． 迄今为止, 不同的混沌保密通信架构已经被提出并证实[2-4], 单向单信道传输速率可以达到30 Gb/s, 传输距离可达100 km以上． 然而, 人们对混沌保密光通信的研究大多局限于单模半导体激光器(semiconductor lasers, SLs)的单信道通信, 这很难满足未来混沌保密光通信在通信速率和通信容量方面的高速发展需求． 因此, 研究者提出了基于波分复用技术(wavelength division multiplexing, WDM)的多信道混沌保密光通信系统[5-12]． 例如, Paul等[5]利用两个外腔反馈单模SLs分别作为发射端提供双信道的混沌载波, 信息经光纤传输后到达接收端进行解密, 实现了双信道的混沌保密通信． Argyris等[7]利用由分布式反馈激光器和波导外腔构成的一对光子集成电路, 实现了1.25 Gb/s加密数据序列的密集波分复用传输． Jiang等[8]提出了一种基于多对SLs的波分复用无源光网络(WDM-PON)方案, 理论实现了多信道的混沌保密通信． 上述研究从实验和理论两方面证明了基于WDM技术的多信道混沌保密光通信的可行性, 从而为未来高速、 大容量混沌保密通信网络的构建和应用提供了一种可行的候选方案．

WDM混沌保密通信系统构建的关键环节之一是寻求大范围波长可调的混沌载波源． 在适当的光反馈、 光电反馈或光注入等外部扰动作用下, SLs容易被驱动到混沌工作态, 且其输出的混沌信号较为复杂, 因而已经成为混沌保密通信中常用的混沌光源． 与传统的单模SLs相比, 法布里-珀罗激光器(Fabry-Perot laser diodes, FPLDs)可同时输出多个模式, 从而为多信道混沌保密通信系统的构建提供了可能． 2004年, Buldu等[13]从理论上研究了基于两个单向耦合FPLDs的多信道通信系统的混沌同步性能和通信性能． 2014年, 操良平等[14]提出了基于光反馈多模SLs的多信道单向混沌通信系统, 数值研究了系统的同步特性及通信性能． 2016 年, Jiang等[15]理论证实了基于多模激光器的安全性增强的WDM混沌保密光通信． 特别地, Lin等[16]在传统FPLDs的基础上研发了弱谐振腔法布里-珀罗激光二极管(WRC-FPLDs)． 与传统FPLDs相比, WRC-FPLDs具于有更长的腔长和更低的前端面反射率, 因而其模式间隔更小, 在一定波长范围内可能存在更多的模式． 基于以上优点, WRC-FPLDs有望成为构建WDM混沌保密光通信系统的理想光源． Zhong等[17]进一步证实了基于滤波反馈WRC-FPLDs可以产生波长大范围可调节的宽带混沌信号以及基于两个单向耦合WRC-FPLDs可实现波长可调谐的混沌保密通信[18]．

众所周知, 实现混沌保密通信的必要前提是发射端和接收端激光器之间实现高质量的混沌同步． 目前大多数混沌同步的研究主要集中在单信道的单向耦合(unidirectional coupling, UC)结构[3-4, 19]． 在这种结构中, 信息被加载到发射端的混沌载波上, 基于两激光器的混沌同步, 在接收端利用混沌滤波效应(chaos pass filtering effect, CPF)可实现信息的有效提取[20-21]． 为进一步提高系统的通信容量, 基于互耦激光器结构的混沌同步实现双向保密通信受到了广泛关注[22-24]． 在对称的互耦合结构中, 由于SLs之间的噪声、 频率失谐及其他内部参量等因素会导致系统自发地出现对称破缺现象, 导致SLs之间的超前-滞后角色发生相应的改变[25-26], 因而难以获得适用于通信的稳定的混沌同步． 为解决混沌同步稳定性的问题, 人们在对称的互耦合结构基础上通过增加反馈环获得了稳定的混沌同步[27-28]． Zhang等[29]提出了一种极度不对称的互耦合混沌保密通信系统, 该系统中没有引入额外的反馈环, 而是通过极度非对称导致的注入锁定效应实现了稳定的混沌同步和双向通信． Deng等[22]基于非对称偏置电流下的互耦合激光器实现了高质量的超前-滞后混沌同步． 由此可见, 非对称互耦合结构的引入为高质量混沌同步的实现提供了一种可行的方式．

本文提出了一种基于两个非对称互注入WRC-FPLDs实现波长可调谐的混沌同步方案． 通过调节互注入光路中可调光滤波器的中心波长和可调衰减器, 可以实现混沌载波波长的自由切换和非对称注入的调整． 两个WRC-FPLDs之间由于较强的非对称光注入导致注入锁定, 从而实现波长可调谐的混沌同步． 此外, 还讨论了非对称注入程度和频率失谐对两激光器对应模式之间混沌同步性能的影响．

1 实验装置

图1为基于非对称互注入WRC-FPLDs的波长可调谐混沌同步实验装置图, WRC-FPLDs分别由两个高精度、 超低噪声的激光器控制器(LC, ILX-Lightwave LDC-3724C)驱动． 在实验过程中, 非对称注入通过分别调节两条路径的注入强度来实现． WRC-FPLD1的输出光经过一个光环形器(OC1)后被50∶50的光纤耦合器(FC1)分为两部分． 其中一部分输出光依次经过可调光滤波器(TOF1, AOS, range: 1 544.00 nm～1 556.00 nm, 3 dB bandwidth: 0.28 nm)、 掺铒光纤放大器(EDFA1)、 偏振控制器(PC1)和可调衰减器(VA1)后, 再次被20∶80的光纤耦合器(FC2)分成两部分, 其中80 %的输出通过OC2的端口1注入WRC-FPLD2, 20 %的输出进入功率计(PM, JW3216C)进行光功率检测． 实验过程中TOF1用于调节WRC-FPLD1的中心波长, PC1和VA1分别用于调节偏振态和注入强度． 从FC1输出的另一部分光通过10∶90的光纤耦合器(FC5)进入测试分析系统． 其中一部分输出光进入光谱分析仪(Aragon Photonics BOSA lite+)以实现光谱的探测, 另一部分输出光通过两个光电探测器(PD1, New Focus 1 544-B, 12GHz bandwidth; PD3, U2T-XPDV2120R, 50 GHz bandwidth)后分别进入数字示波器(OSC, Agilent X91604A, 40 GSa/s, 16 GHz bandwidth)和频谱分析仪(ESA, R&S FSW, 67 GHz bandwidth)以分析混沌信号的时间序列和相应的功率谱． WRC-FPLD2输出光的传输路径与WRC-FPLD1类似, 且PD1和PD2, PD3和PD4的型号一致．

2 实验结果与讨论

图2为WRC-FPLD1和WRC-FPLD2自由运行时的光谱, 两个WRC-FPLDs的偏置电流分别固定在I1=55.00 mA,I2=35.00 mA, 温度分别设定为T1=21.00 ℃和T2=19.50 ℃． 从图2可以看出, 两个激光器在自由运行状态下可在1 535～1 565 nm的范围内输出多达50个模式, 模式间隔约为0.57 nm． 由于两激光器的纵模间隔几乎相同, 因此两激光器对应纵模之间的频率失谐被定义为Δf=f1-f2, 其中f1和f2分别为WRC-FPLD1和WRC-FPLD2对应模式的频率． 耦合强度κ12和κ21分别定义为WRC-FPLD1注入WRC-FPLD2的光功率与WRC-FPLD2自由运行时的输出功率之比, 以及WRC-FPLD2注入WRC-FPLD1的光功率与WRC-FPLD1自由运行时的输出功率之比． 在整个实验中, 通过固定WRC-FPLD2的温度和调节WRC-FPLD1的温度, 可以调节频率失谐Δf． 考虑到各个模式的情况基本一致, 为了简便, 本文仅仅考虑了两个模式的情况．

图2 WRC-FPLD1和WRC-FPLD2自由运行时的光谱

图3为WRC-FPLD1和WRC-FPLD2输出的两个模式所对应的时间序列(图3a,3b)、 功率谱(图3c, 3d)、 光谱(图3e, 3f)和互相关系数(图3g, 3h)． 图3a,3c,3e,3g分别对应λ=1 551.416 8 nm,κ12=2.032,κ21=0.022,Δf=-5 GHz, 图3b,3d,3f,3h分别对应λ=1 553.453 0 nm,κ12=3.732,κ21=0.023,Δf=-5 GHz． 从图3a,3c,3e和图3b,3d,3f可以看出, 两个激光器对应模式均工作在混沌态, 其光谱展宽, 功率谱变得平滑． 从图3g和图3h可以看出, 通过调节非对称注入强度和频率失谐, WRC-FPLD1的输出滞后于WRC-FPLD2的输出, 两个模式间实现了高质量超前-滞后混沌同步, 最大的同步系数均位于-260 ns附近(对应两个激光器之间的距离)且最大互相关系数Cmax分别为0.90和0.87. 在本实验中, 由于κ12远大于κ21, WRC-FPLD1的输入光驱动WRC-FPLD2工作在混沌态并实现了注入锁定, 从而使系统获得了高质量的超前-滞后混沌同步． 需要指出的是, 两个激光器超前或滞后的角色可以互换, 这本质上取决于互注入双方各自输出功率与被注入功率的关系, 两个激光器因此可分别工作于被注入锁定的状态．

a,b对应时间序列; c,d对应功率谱; e,f对应光谱; g,h对应互相关系数． a,c,e,g分别对应λ=1 551.416 8 nm, κ12=2.032, κ21=0.022, Δf=-5 GHz; b,d,f,h分别对应λ=1 553.453 0 nm, κ12=3.732, κ21=0.023, Δf=-5 GHz．

图4为无频率失谐情况下, 两个激光器相应模式间最大相关系数Cmax随耦合强度κ12的变化曲线, 其中耦合强度κ21分别固定为0.022和0.023. 从图中可以看出, 两个模式的最大互相关系数曲线呈现出了相似的变化趋势． 随着κ12的增加,Cmax迅速增大并最终保持在一个较高水平． 这一现象可以解释为: 当κ12较小时, 两个激光器的角色相当, 在互注入作用下无法达到较好的同步． 随着κ12的增加, WRC-FPLD1的主导地位越来越明显, 在非对称互注入作用下WRC-FPLD2输出逐渐趋向于与WRC-FPLD1的输出一致． 当κ12增大到一定程度后, WRC-FPLD1在非对称互注入中扮演了主导角色, WRC-FPLD2被WRC-FPLD1注入锁定, 因此两个激光器相应的模式之间可以达到高质量的混沌同步． 随着κ12的进一步增大, 极度非对称互注入结构使激光器之间的注入锁定效应得到进一步加强, 混沌同步质量被稳定在一个较高的水平． 由图3和图4可知, 在一定的频率失谐下, 两个互注入激光器间非对称程度的增加有利于系统实现高质量混沌同步．

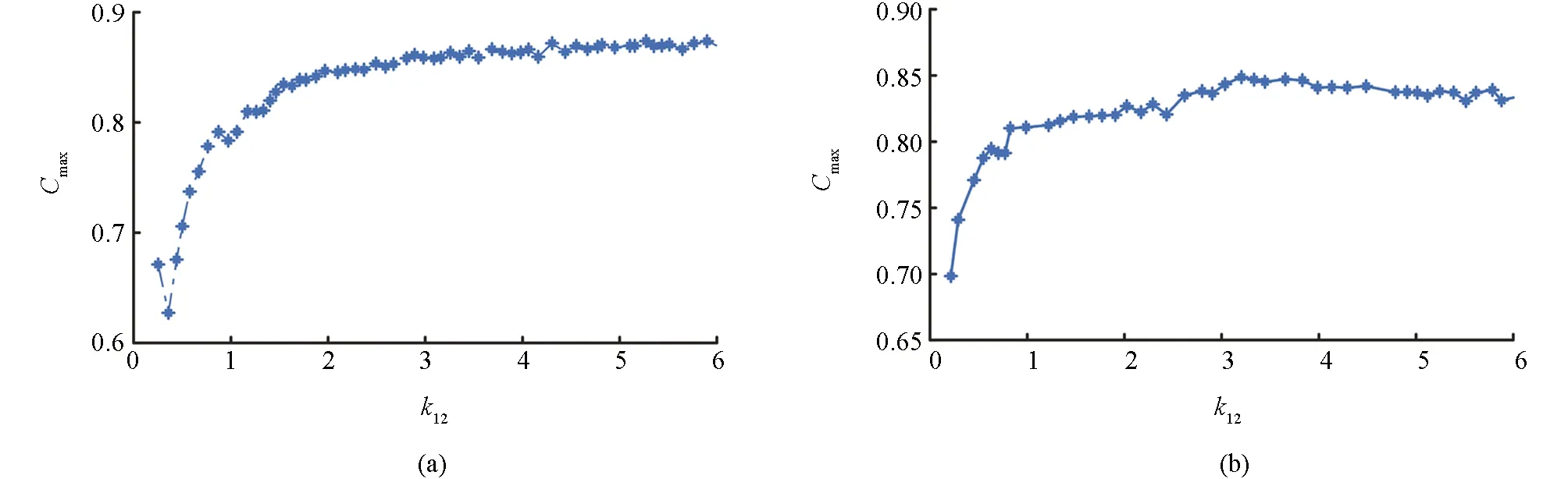
κ21分别固定在0.022和0.023, 波长λ 分别为1 551.416 8 nm和1 553.453 0 nm．

图5给出了不同频率失谐下Cmax随κ12的变化曲线． 从图5中可以看出, 与零失谐的情况相比, 在一定的频率失谐下, 两个模式的Cmax随κ12的变化整体上仍然呈现相似的变化趋势． 此外, 由于光注入导致的波长红移现象, 适当的负频率失谐有助于系统实现注入锁定, 从而提高系统的同步性能． 相反, 正频率失谐注入将进一步扩大两个激光器之间由于互注入引起的频率之差, 弱化注入锁定效应, 从而使同步性能恶化． 因此, 在我们的实验条件下, 相比于正频率失谐, 适当的负频率失谐有助于获得更高质量的混沌同步．

Δf分别为+5 GHz, +10 GHz, -5 GHz, -10 GHz, κ21分别为0.022,0.023．

图6给出了Cmax随Δf变化的曲线, 其中κ12分别为2.032和3.732,κ21分别为0.022和0.023． 从图6中可以看出, 与零失谐的情况相比, 正失谐的增加会降低系统的同步性能, 而适当的负失谐有助于提高系统的同步性能, 进一步增大负失谐同样会降低系统的同步性能, 这些结果与图5中的情况基本一致． 由此可见, 通过增加两个激光器注入的非对称程度和采用适当的负频率失谐将有助于系统获得高质量混沌同步．

(a) κ12=2.032, κ21=0.022, λ=1 551.416 8 nm; (b) κ12=3.732, κ21=0.023, λ=1 553.453 0 nm．

3 结论

本文提出了基于两个非对称互注入WRC-FPLDs的波长可调谐的混沌同步系统, 实验研究了该系统的同步性能． 实验结果表明, 通过改变可调滤波器TOF的中心波长和两条路径的注入条件, WRC-FPLDs输出的不同模式均可实现混沌输出． 通过分别控制两条路径的注入强度可以构建非对称互注入结构, 并实现超前-滞后混沌同步． 增强互注入的非对称程度并采用适当的负频率失谐可有效增强注入锁定效应, 从而提高系统混沌同步质量．