不同尾翼结构火箭弹动态气动特性数值研究

甘语怀,杨丽君,罗 念,王纪林,王元豪

(西南技术工程研究所, 重庆 400039)

0 引言

尾翼稳定是火箭弹空中飞行的稳定方式之一,是依靠尾翼将火箭弹全弹压力中心移至质心之后,产生稳定力矩从而保证火箭弹稳定飞行[1]。火箭弹动导数是其机动性或受扰动飞行状态下是否具有稳定性的一个重要判据,关系飞行安全和战技指标的实现[2],因此,基于火箭弹静态气动特性分析研究已经不能满足先进武器的设计要求,关于火箭弹动态稳定性分析的研究具有重要的价值与意义[3-4]。

刘金等[5]研究了短钝外形飞行器的动稳定特性,在亚跨超声速风洞中完成了某短钝外形飞行器俯仰动导数的测量,获取了俯仰动不稳定状态点;柴振霞等[6]运用Etkin非定常气动力模型,运用谐波平衡法对WR-A这种复杂外形飞行器动态导数辨识,表明了谐波平衡法在保证精度的同时,具有较高的计算效率;王海鹏等[7]总结归纳了俯仰方向各种动导数的计算方法,以NACA0012翼型为例计算了动导数,与风洞试验数据进行对比,证明了计算方法的正确性;陈亮等[8]以新型掠飞末敏弹为研究对象,分析了不同马赫数下掠飞末敏弹滚转运动对其俯仰组合动导数和升力系数动导数的影响规律,同时,研究了滚转和锥进运动对动导数求解的影响[9];米百刚[10]基于CFD方法,开展了动稳定性导数快速精细计算分析和大迎角非定常气动力模型开发等相关问题的研究;邓维[11]以某鸭式布局弹箭研究对象,计算了其俯仰阻尼动导数及其随初始条件的变化规律。

本文中主要研究3种尾翼结构火箭弹在不同飞行状态下的动态气动特性,确定了俯仰组合动导数的计算公式,求解了俯仰组合动导数,对比分析了3种尾翼结构火箭弹的动态气动特性差异。

1 物理模型

1.1 计算模型

本文中研究对象为3种不同尾翼结构火箭弹,即四卷弧翼火箭弹(4-wrap-aroundfins,简写为4-WAF)、六卷弧翼火箭弹(6-wrap-aroundfins,简写为6-WAF)以及六平板尾翼火箭弹(6-flatfins,简写为6-FLF)。

3种尾翼结构火箭弹模型共用相同的弹身,在尾翼结构以及数量方面存在差异,并且尾翼均能折叠到相同的弹径尺寸。3种尾翼结构火箭弹的尾翼投影面基本尺寸、尾翼展长以及弹身尺寸,如图1—图3所示。

图1 尾翼投影面尺寸Fig.1 Pojection surface dimension of wings

图2 火箭弹尾翼展长Fig.2 Wings span of rockets

图3 火箭弹弹身尺寸Fig.3 Body size of rockets

为使仿真计算能够顺利进行,需要对3种尾翼结构火箭弹模型进行必要的简化,简化后的火箭弹3维模型如图4所示,模型主要包含弹体和尾翼等2个部分。

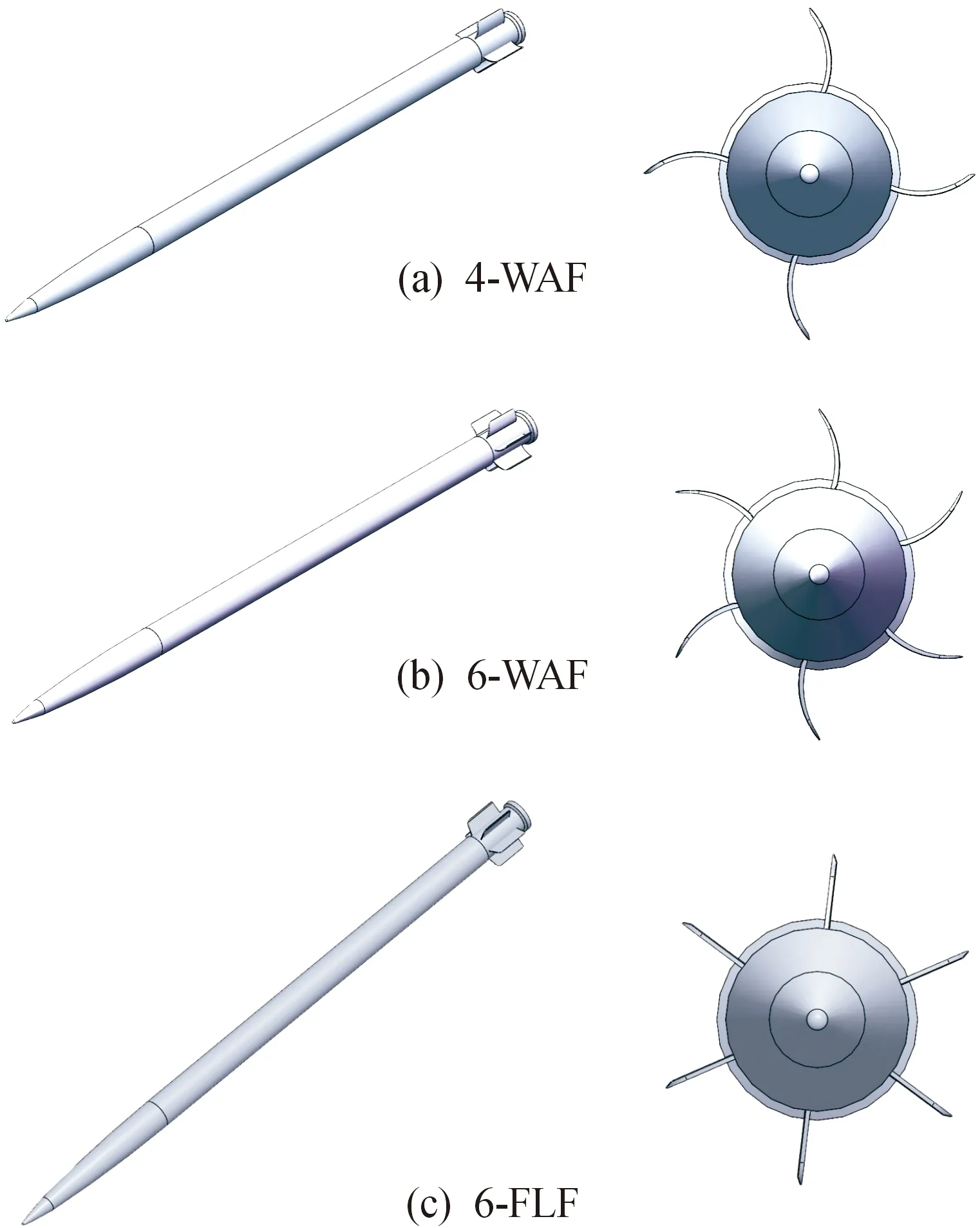
图4 火箭弹模型Fig.4 Rocket model

1.2 网格划分

采用混合网格划分方法对3种尾翼结构火箭弹流场区域进行网格划分,流场划分成2个子域,即靠近弹体的近场域和包围近场域的远场域。近场域为平动域,远场域为旋转域,模型计算域如图5所示。

图5 模型计算域Fig.5 Model calculation domain

图6(a)为火箭弹近场域网格,该区域网格包裹整个弹体;为减少流场计算域边界对仿真结果的影响,远场域需要足够大,因而将远场域边界取为弹前和弹后空间间距10倍弹长,周向空间取为200倍弹径,如图6(b)所示。近场域网格和远场域网格分别划分,各自生成计算域网格后进行合并,合并后的总网格作为火箭弹外流场计算域。

图6 火箭弹外流场计算域网格划分Fig.6 Rocket outflow field calculation domain grid division

2 数值计算方法

强迫振动法是求解动导数最为广泛的CFD方法,这种方法适应性强,不受飞行状态限制,可以用来计算全马赫数下的动导数,是代表非线性气动力特性预测的最为先进的方法,且具有较高的计算精度[12],本文中基于强迫振动法计算3种尾翼结构火箭弹的动导数。

2.1 计算方法

基于小幅度强度振动的方法求解纵向组合动导数时,对应的非定常运动为俯仰谐和振动,假设强迫飞行器绕其重心做小幅度的正弦俯仰振荡时,其运动规律为:

θ=θ0sin(ωt)

(1)

角速度为振幅的一阶导数,因此有:

(2)

当自由来流不发生变化时,俯仰角速度ωz与迎角变化率形式一致,则:

Δα=θ=sin(ωt)

(3)

式(1)—式(3)构成了非定常运动的运动方程。基于气动力导数的概念,刚体飞行器所受的非定常气动力/力矩可以表示为:

(4)

在中小迎角范围内,气动力常常表现为线性或者弱的非线性,对式(4)略去高阶项,只保留前4项,代入运动方程可表示为:

(5)

对于式(5)描述的非定常运动过程,若时间足够长时,谐和振荡产生的非定常气动力将趋于周期性变化,此时令ωt=2nπ,则式(5)可以改写成:

(6)

一般来说,计算动导数的公式均为无量纲,现引入减缩频率k=ωc/2V,可得到无量纲化的组合动导数计算公式为:

(7)

式(7)中,Cωt=2nπ和Cmz0均通过数值模拟获取,前者为非定常流场周期稳定后求解可得,后者为初始迎角时的平衡力矩,由定常流场求解得到。该方法由于强调了瞬态效应,仅仅使用了单点的气动数据辨识动导数,因此称为单点法,本文中运用单点法求解动导数。

通过单点法计算的组合动导数,已进行无量纲化处理,组合动导数的绝对值越大,表明动态稳定性越高。

2.2 仿真工况

准确地预测火箭弹飞行过程所受的瞬时力矩是使用非定常方法求解动导数的关键。本文中选取β0=0°为计算状态,减缩频率取为k=0.01,振幅取为βm=0.25°,则振荡规律方程为:

β=β0+βmsin(ωt)=0.25sin(ωt)

(8)

本小节基于小振幅强迫谐和振动法,求解3种尾翼结构火箭弹的纵向非定常气动力,即俯仰组合动导数,仿真工况以及谐和振荡方程如表1所示。

表1 仿真工况及振荡方程Table 1 Simulation conditions and oscillation equations

3 计算结果与分析

图7为来流攻角α=0°时,4-WAF、6-WAF以及6-FLF通过小幅度强迫谐和振动方法仿真计算所获得的瞬时力矩系数Cm随瞬时攻角β的变化曲线,由于在来流攻角α=0°时,瞬时力矩系数Cm数值远小于瞬时攻角β,因此对瞬时攻角β做了缩放处理。

图7 “迟滞”现象Fig.7 Hysteresis phenomenon

由图7曲线可以看出,3种尾翼结构火箭弹瞬间力矩系数均滞后于瞬时攻角,瞬时力矩系数与瞬时攻角之间存在迟滞角,呈现“迟滞效应”,这是非定常计算时的典型现象,反映了仿真计算时响应对输入强迫振动信号的滞后;对比4-WAF、6-WAF以及6-FLF的迟滞角可知,图7中各迟滞角大小并不一致,可能的原因是计算域网格数量和网格质量的差异,造成计算机在仿真计算时对输入强迫信号响应时间的不同,“迟滞效应”只是反映了对输入强迫信号的响应快慢,并不影响计算结果,因而迟滞角的不同不影响仿真计算结果。

图8为Ma=0.8时,4-WAF、6-WAF以及6-FLF在来流攻角α=0°和α=5°时俯仰力矩系数迟滞环。图8为0.8Ma下不同攻角时3种尾翼结构火箭弹瞬时力矩系数随瞬时攻角的变化情况,由图8可知,瞬时力矩系数随着瞬时攻角的增加呈环形分布,构成迟滞环。图8(a)为0.8Ma,α=0°下3种尾翼结构火箭弹瞬时力矩系数“迟滞环”,由图8(a)曲线可知,6-WAF俯仰力矩系数“迟滞环”绝对值大于6-FLF,表明卷弧翼火箭弹的动态飞行稳定性更高。图8(b)为0.8Ma,α=5°下3种尾翼结构火箭弹瞬时力矩系数“迟滞环”,由图8(b)曲线可知,6-WAF俯仰力矩系数“迟滞环”绝对值大于4-WAF,表明增加卷弧翼数量后,卷弧翼火箭弹的动态飞行稳定性更高。

通过对比图8(a)、图8(b)可知,攻角增大,3种尾翼结构火箭弹瞬时力矩系数数值成倍数增大,表明在小攻角下,攻角越大,火箭弹动态飞行稳定性越高。

在不同马赫数下时,4-WAF、6-WAF以及6-FLF俯仰力矩系数“迟滞环”呈现相同的变化趋势,因而不再赘述。

图9为来流攻角为α=0°和α=5°时,4-WAF、6-WRF以及6-FLF俯仰组合动导数随马赫数的变化规律。由图9(a)和图9(b)可知,4-WAF、6-WRF以及6-FLF俯仰组合动导数绝对值随着马赫数的增加而增大,这表明火箭弹的动态稳定性随着马赫数的增加而增加。

图9 不同攻角下的俯仰组合动导数随马赫数的变化规律Fig.9 Variation of pitching combined dynamic derivative with Mach number at diffirent angles of attack

由图9(a)可知,在来流攻角α=0°时,随着马赫数的变化,6-WRF俯仰组合动导数绝对值始终大于4-WAF,表明增加卷弧翼数量后,卷弧翼火箭弹的俯仰组合动导数增大,动态稳定性增加;同时可以看出,6-WRF俯仰组合动导数绝对值始终大于6-FLF,表明相同尾翼数量的卷弧翼火箭弹和平板尾翼火箭弹相比,卷弧翼火箭弹动态稳定性更高。当来流攻角α=5°时,通过对比图9(b)中3组曲线可以得出相同的结论。

表2为3种尾翼结构火箭弹不同马赫数下俯仰组合动导数随攻角的变化情况。由表2可知,随着攻角的增加,4-WAF、6-WRF以及6-FLF俯仰组合动导数绝对值增加,表明随着攻角的增加,火箭弹动态稳定性增加。

表2 不同马赫数下俯仰组合动导数随攻角的变化情况Table 2 The variation of pitching combined dynamic derivative with angles of attack at different Mach number

通过对比不同攻角下4-WAF和6-WRF俯仰组合动导数可知,在不同攻角下,6-WRF俯仰组合动导数绝对值大于4-WAF,表明不同攻角下6-WRF的动态稳定性更强。

通过对比不同攻角下6WAF和6-FLF俯仰组合动导数可知,在不同攻角下,6-WRF俯仰组合动导数绝对值大于4-WAF,表明不同攻角下,卷弧翼火箭弹的动态稳定性高于平板尾翼火箭弹。

综合上述分析,在小攻角范围内,攻角越大,3种翼型火箭弹动态飞行稳定性越高;增加卷弧翼的数量后,能使得卷弧翼火箭弹有更大的动态飞行稳定性;同时,平板尾翼火箭弹的俯仰组合动导数绝对值小于卷弧翼火箭弹,动态飞行稳定性低于卷弧翼火箭弹。

4 结论

本文中主要研究3种尾翼结构火箭弹动态气动特性,确立了火箭弹动导数辨识方法,对3种尾翼结构火箭弹俯仰组合动导数进行了仿真计算以及对比分析,结果表明:

1) 随着马赫数的增加,3种尾翼结构火箭弹的俯仰组合动导数绝对值增加,且6-WAF俯仰组合动导数大于4-WAF,表明增加卷弧翼的数量可以提升卷弧翼火箭弹的动态飞行稳定性。

2) 6-WAF俯仰组合动导数绝对值大于6-FLF,表明平板尾翼动态稳定性稍低于卷弧翼。

3) 3种尾翼结构火箭弹俯仰组合动导数随着攻角的增大而增大,表明在小攻角范围内,攻角越大,动态飞行稳定性越高。