基于DACO-BP的水下聚能装药峰值超压预测

刘 芳,张峻豪,卢 熹,郭策安

(1.沈阳理工大学 理学院,沈阳 110159;2.辽宁省兵器工业智能优化与控制重点实验室, 沈阳 110159;3.沈阳理工大学 自动化与电气工程学院,沈阳 110159;4.沈阳理工大学 装备工程学院,沈阳 110159)

0 引言

战斗部装药爆炸冲击波可以毁伤人员、装备和设施等各种军事目标,作用范围大、破坏力强,爆炸冲击波的毁伤效果是装药质量和性能的重要衡量指标,在战斗部设计中占有重要地位[1]。装药冲击波的毁伤效果主要取决于3个参数,分别是峰值超压、正压作用时间和比冲量[2],其中峰值超压是评判冲击波威力评估的关键参数。

近几年,学者们分别从数值模拟和物理模型2个方面研究冲击波峰值超压参数的预测方法,取得了一些成果。基于数值模拟方面,王维[3]等人采用AUTODYN-2D软件对装药在空气中爆炸的情况进行一维数值模拟与有一定地面爆高高度的二维数值模拟,分析高度对峰值超压预测值的影响。LUO Haohao等[4]利用NUBOX-9012冲击波监测仪对现场爆炸冲击波进行监测,采用有限元软件ANSYS/LS-DYNA模拟井下直通式巷道爆破冲击波的衰减过程,提出峰值超压预测公式。王岩等[5]采用ANSYS/LS-DYNA软件对火箭飞行至0～20 km高度爆炸进行了有限元仿真分析,提出了考虑高度效应的火箭空中爆炸冲击波峰值超压预测公式。基于物理模型方面,秦毅等[6]结合已有文献实验数据,利用光滑层流火焰传播理论模型建立了爆炸超压模型。李彦超等[7]通过揭示当量比对氢气云爆炸火焰形态、火焰半径和爆炸超压峰值的影响规律,建立耦合火焰自加速传播的氢气云爆炸超压预测模型。

上述方法通过数值计算或物理模型求解,获得典型条件下战斗部的载荷数据,根据数据规律来拟合相关参数的峰值超压预测公式或预测模型,只能解决特定规格、特定结构的装药超值超压预测问题,缺少综合考虑装药结构参数对装药超值超压数值的影响,泛化性能欠缺,非线性处理能力弱、智能性不足,不能满足现代军事对弹药设计的智能化需求。随着人工神经网络的发展,BP神经网络具有良好的非线性映射能力和泛化性能,使综合考虑装药结构参数的智能化峰值超压预测成为可能。

综上所述,针对传统超值超压预测模型存在的问题和现代军事对装药超值超压预测的智能化需求,开展考虑装药结构参数的智能聚能战斗部峰值超压预测模型研究。利用数值仿真软件AUTODYN,获得不同长径比装药的沿轴向与径向坐标分布的峰值超压数据,采用梅森旋转算法对数据随机排序,提高模型的泛化能力。考虑战斗部结构参数与峰值超压数值非线性关系较强,构建一种动态自适应蚁群算法优化BP神经网络(DACO-BP)模型对水下聚能装药的峰值超压进行预测。设计包含8个智能预测模型的对比实验,采用精度指标、速度指标、稳定性指标来评价模型,验证DACO-BP水下聚能装药峰值超压预测算法的有效性、稳定性。通过水下爆炸峰值超压Cole经验公式[8]说明模型预测结果的可信性。

1 实验参数数值求解

聚能装药水下爆炸过程属于非线性瞬态流固耦合问题[9],文献[10]采用数值仿真软件AUTODYN,模拟了水下聚能装药爆炸的过程,构建了聚能装药水下的爆炸仿真模型,通过与试验数据对比结果,验证模型的可信性。本文利用文献[10]建立的数值仿真模型求解聚能装药水下爆炸冲击波峰值超压参数。仿真模型如图1所示,其中主装药为B炸药、直径为72 mm。药型罩采用球缺结构,材料为紫铜,壳体及端盖材料为铝,厚度为2.7 mm。装药前向水域中设置了36个观察点(图1中的1～36)用于捕捉爆炸时冲击波的相关数据。

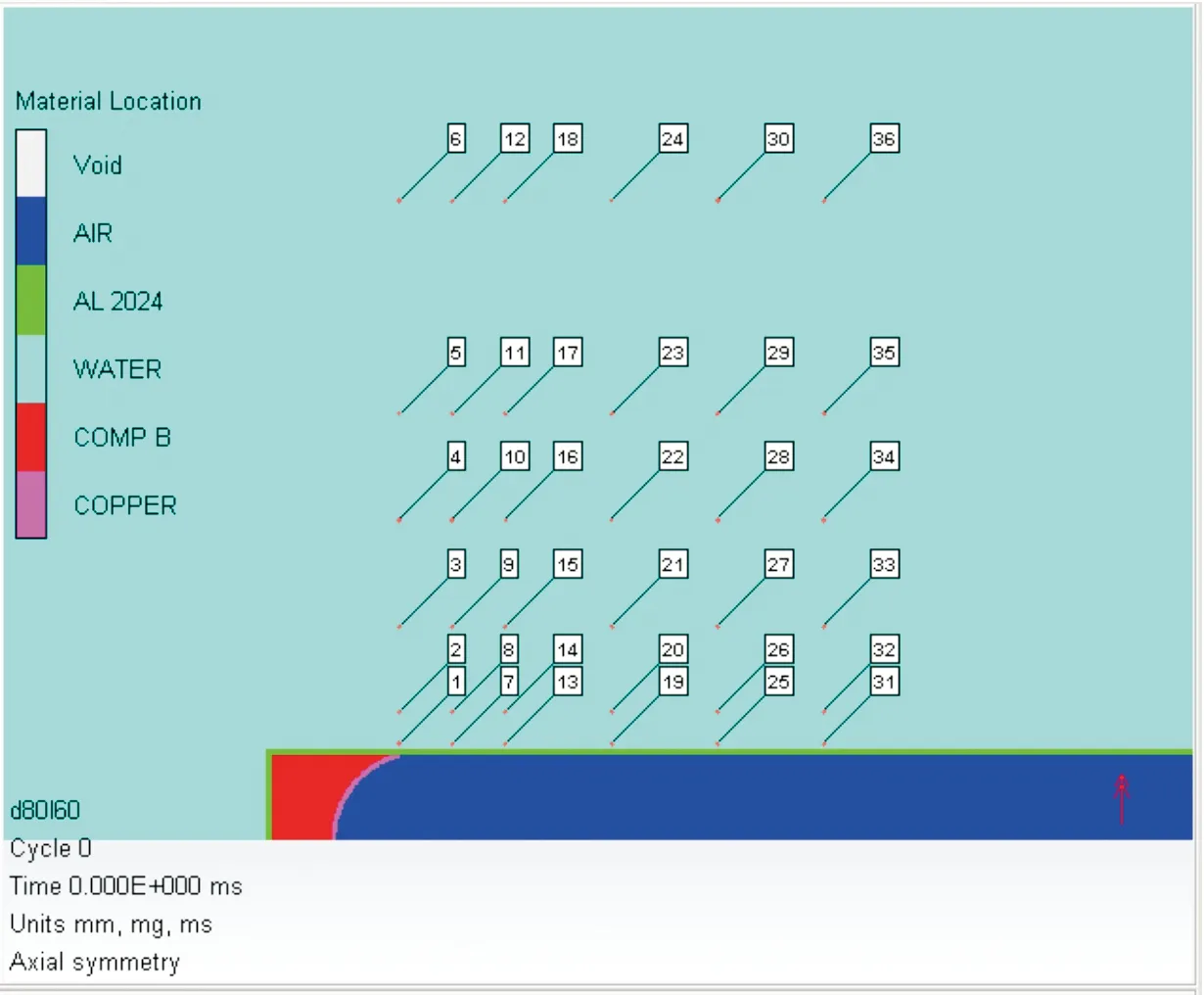
图1 仿真模型Fig.1 Simulation model

选取相关的条件参数为装药结构尺寸和测点位置参数,预测数值为爆炸冲击波传播至不同位置处的峰值超压,装药条件参数与预测数值如表1所示。

表1 装药条件参数与预测数值Table 1 Charge condition parameters and prediction value

2 梅森旋转算法

梅森旋转算法(mersenne twister)是由M.Matsumoto and T.Nishimura提出的伪随机数算法,该算法是一种周期长、内存小、稳定性高、生成随机数质量较优的伪随机数发生成器[11]。算法的递推公式采用模2类运算,产生二进制的随机数位,从而构成随机数[12]。递推公式为:

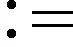
(1)

(2)

该递推公式简化为位移运算,位移公式为:

(3)

式(2)中,y=(yw-1,yw-2,…,y0)。

y=(yw-1,yw-2,…,y0)由于该特征多项式展开后共有100多项,因此算法具有较高随机性。为提升模型适应不同数据分布的泛化,采用梅森旋转算法对数据进行随机排序,数据随机互换流程图如图2所示。

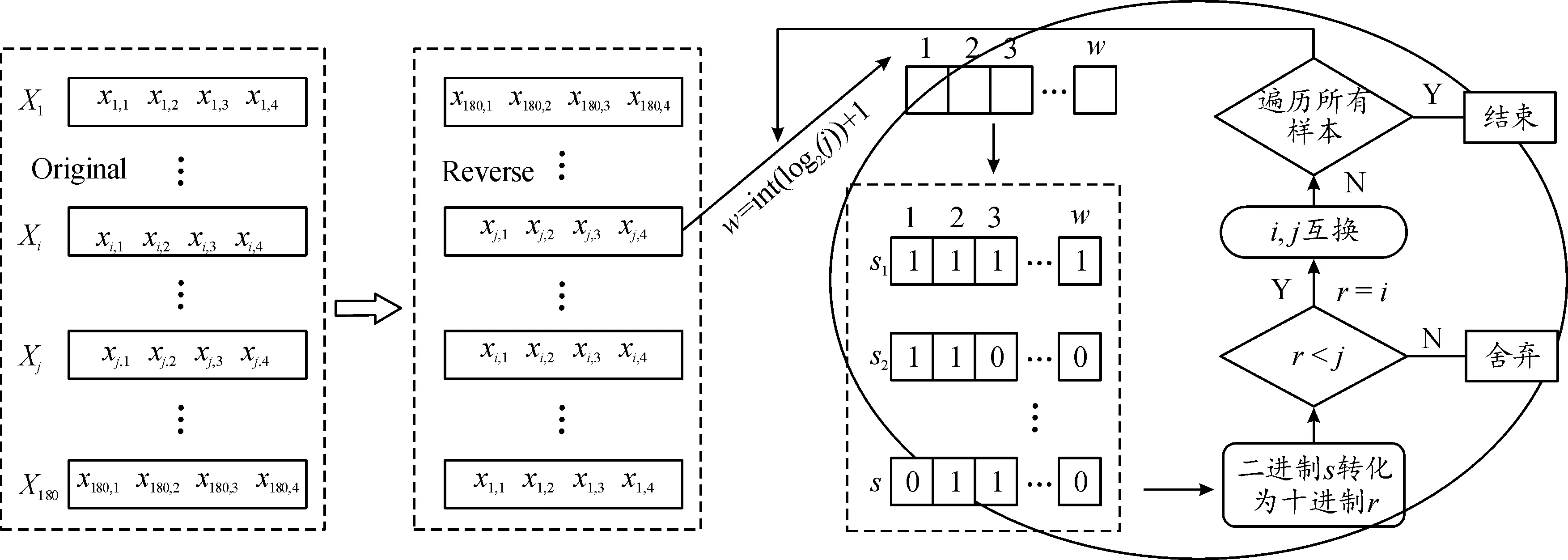
图2 数据随机互换流程Fig.2 Flow chart of random data exchange

3 动态自适应蚁群算法(DACO)和BP神经网络

3.1 传统蚁群算法(ACO)

蚁群优化算法(ant colony optimization,ACO)是由M.Dorigo等人提出的一种模拟蚂蚁觅食的仿生智能算法[13]。蚁群算法的核心策略由蚂蚁的路径选择和信息素的更新策略2个部分组成。蚂蚁路径选择策略如式(4)所示,信息素更新策略如式(5)和式(6)所示。

(4)

τj(Iθi)(t+k)=(1-ρ)*τj(Iθi)(t)+Δτj(Iθi)

(5)

(6)

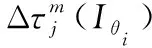
信息素的挥发机制是影响蚁群算法性能的主要因素。传统蚁群算法中,路径上的信息素按照固定的挥发系数挥发,没有考虑算法的迭代次数、迭代时适应度值变化和整个种群适应度值的变化对不同路径上信息素量值的影响,会导致算法易陷入局部最优值[16]。同时,算法的迭代前期是信息素累积过程,这时信息素挥发较多会导致迭代前期信息素增长缓慢,降低算法收敛速。

3.2 动态自适应蚁群算法(DACO)

针对传统蚁群算法易陷入局部最优解、收敛速度慢的问题,本文设计动态自适应蚁群算法,改进传统蚁群的信息素挥发机制。在算法的迭代前期,采用信息素纯增长策略,解决传统蚁群前期路径信息素匮乏问题,提升算法的收敛速度。信息素更新策略为:

τj(Iθi)(t+k)=τj(Iθi)(t)+Δτj(Iθi)

(7)

在算法的迭代中后期,综合考虑蚂蚁的迭代次数、蚂蚁迭代时适应度值变化和整个种群适应度值的变化,设计挥发系数双曲线动态自适应调整策略,根据蚁群每一次迭代适应度值的变化,调节挥发系数ρ,信息素更新如式(5)所示,信息素挥发策略如式(8)所示。

(8)

式(8)中,挥发系数ρ由指数函数L(x)和sigmoid函数K(x)自动调整,ρ在(ρmin,ρmax)之间取值。函数L(x)与K(x)计算式分别为:

L(x)=e(x-Nmax)*α

(9)

(10)

式(9)中,Nmax为迭代最大次数,α>0为形状因子。L(x)函数前中期增长缓慢,后期增长较快。式(10)中,σ为位置参数,设置其值为Nmax迭代次数的一半,β>0为形状因子。函数关于(σ,0.5)中心对称。K(x)函数在中间部分增长幅度较快,两端增长幅度较慢。挥发系数更新策略示意图如图3所示。

图3 挥发系数更新策略Fig.3 Volatilization coefficient update strategy

如图3所示,前期采用纯信息素增长策略,完成信息素积累。中后期采用挥发系数双曲线动态自适应调整策略,自动调整挥发系数。当蚁群在当前迭代的最小适应度值低于迭代累计蚁群的最小适应度值时,说明本次迭代的蚂蚁选择路径方向正确,加快挥发系数增长的步伐,增加蚁群在正确道路上的收敛速度。否则,降低挥发系数的增长步伐。DACO算法在保证了整个蚁群的收敛速度的基础上,相应的提升了全局搜索能力,避免了传统ACO算法容易陷入局部最优解的问题。

3.3 BP神经网络

BP神经网络包括信息的正向传播,误差的反向传播2个阶段,可以实现从输入空间到输出空间的高度非线性逼近[16]。BP网络通过不断更新网络的权值和阈值,使最后的信号误差达到允许范围之内。本文采用三层BP神经网络,算法预测步骤如下:

Step1:初始化网络参数。初始化神经网络的权值和阈值,设置输入层e、隐含层h与输出层g节点的个数,网络训练次数,学习率lr,最小误差ε。

Step2:计算隐含层节点h(h=1,2,…,H)的输出值yh。

(11)

式(11)中:V(·)表示隐含层的激活函数;ωeh表示输入层节点e到隐含层节点h的连接权值;xe为输入值;bh为隐含层节点h的阈值。

Step3:计算输出层节点g(g=1,2,…,G)的输出值zg。

(12)

式(12)中:U(·)表示输出层的激活函数;ωhg表示隐含层节点h到输出层节点g的连接权值;bg为输出层节点g的阈值。

Step4:训练BP神经网络,网络适应度函数J为:

(13)

3.4 DACO-BP算法

BP神经网络在训练时初始随机赋予权值和阈值,是影响模型有效性和稳定性的主要因素。本文设计DACO-BP算法,将DACO算法获取最优的权值和阈值,映射到BP神经网络,有利于减少模型预测的波动,提高模型预测的有效性和稳定性。算法具体步骤如下:

Step1:将MT算法打乱后的样本数据化分为训练集和测试集进行归一化处理。

(14)

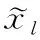
Step2:建立三层神经网路拓扑结构e×h×g。

Step3:初始化蚁群算法相关参数。

Step4:启动全部蚂蚁进行训练,DACO算法根据式(5)—式(8)更新信息素浓度。

Step5:重复Step4,当DACO算法误差小于当前误差或为最大迭代次数,算法跳出循环转为Step6。

Step6:将DACO算法训练后,获取最优的权值和阈值集合映射到BP神经网络。训练BP神经网络直到满足BP算法的误差收敛条件或达到算法最大迭代次数。

Step7:预测数据进行反归一化处理,还原数据原始形态。

(15)

DACO-BP算法伪代码如下:

Initialize ant colony parameters;

Training begins;

while (iterations_num<=iterations_num_max)

if (iterations_num<=N1)

{Pure pheromone growth strategies;}

elseif

{Strategy of hyperbolic dynamic adaptive adjustment of volatilization coefficient;}

end

for i=1:antnum

{Ant i chooses the path based on the

pheromone concentration;}

{Calculate the output error of ant i;}

End

error_min={Find the smallest error

among all ants;}

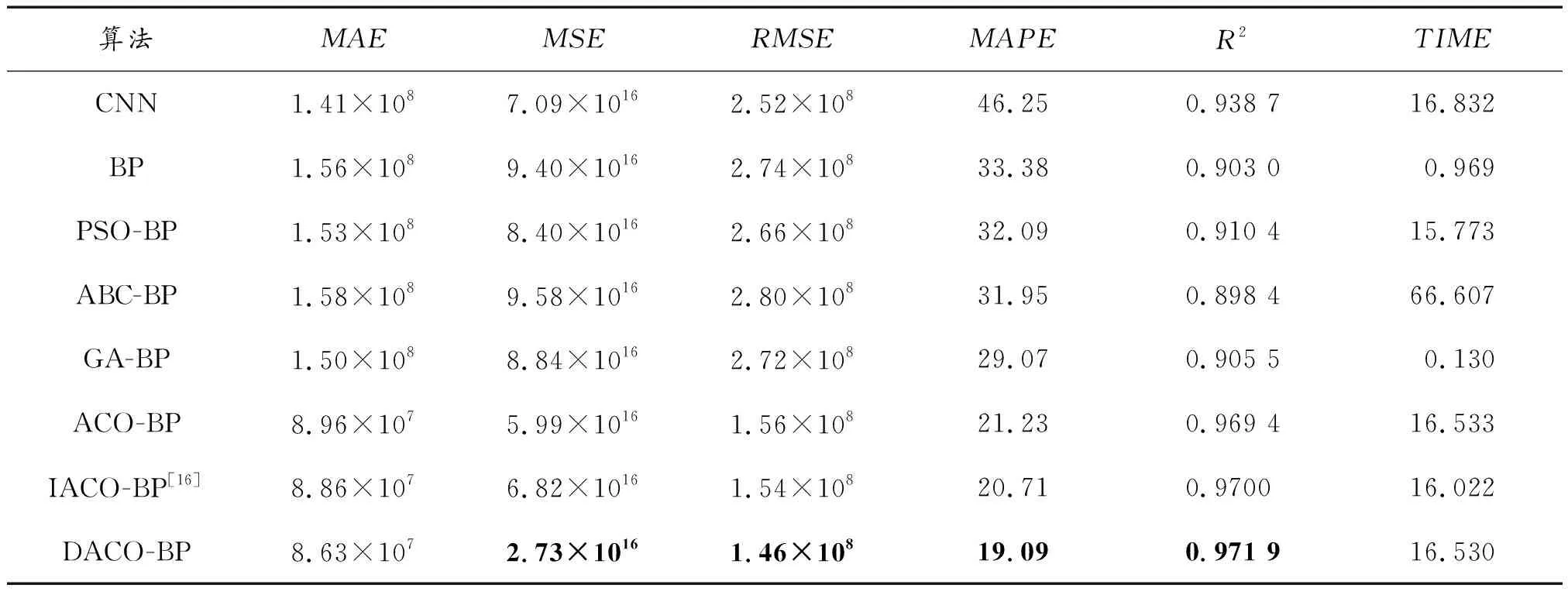
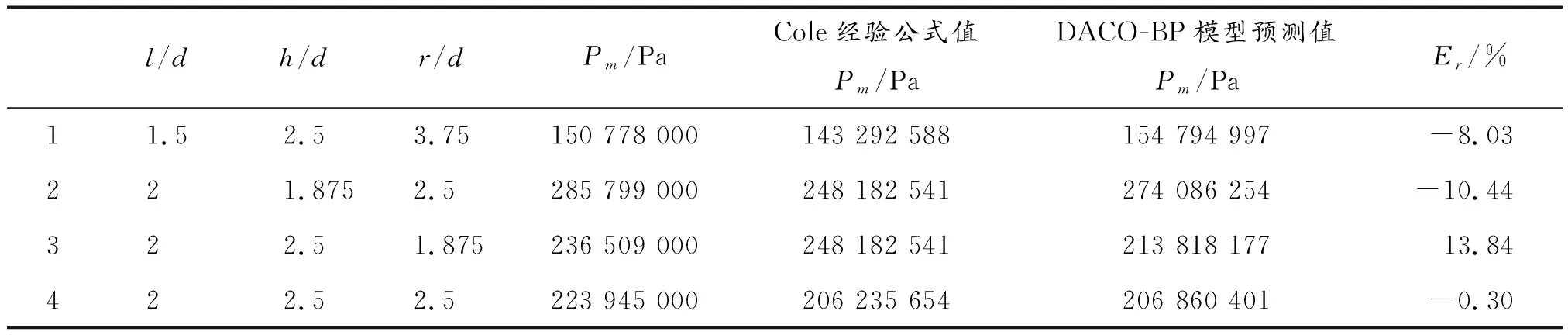
if (error_min

break;

end

end

{

Find the optimal weight and threshold

corresponding to the smallest error;

Use the optimal solution as the initial

solution of the neural network;

Neural network training;

result=The result of neural network training;

}

4 实验仿真及结果分析

为了验证动态自适应蚁群算法优化BP神经网络的有效性和稳定性,采用平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)、拟合优度(R2)和算法运行时间等6个性能指标评估算法的有效性。采用均值(Mean)、方差(Variance)、标准差(Standard)和极差(Range)等4个性能指标评估算法的稳定性。将动态自适应蚁群优化BP神经网络(DACO-BP)与卷积神经网络CNN、BP神经网络、粒子群算法优化BP神经网络(PSO-BP)、人工蜂群算法优化BP神经网路(ABC-BP)、遗传算法优化BP神经网络(GA-BP)、蚁群算法优化BP神经网络(ACO-BP)、改进蚁群算法优化BP神经网络(IACO-BP)算法的结果进行实验对比。为了验证动态自适应蚁群算法优化BP神经网络的的可信性,通过计算Cole经验公式得出的峰值超压值与DACO-BP算法预测的峰值超压值的相对误差来评估算法的可信性。

4.1 实验评价指标

实验选取的5个精度指标MAE、MSE、RMSE、MAPE、R2计算方法如式(16)—式(20)所示。

(16)

(17)

(18)

(19)

(20)

实验选取的4个稳定性性能指标Mean、Variance、Standard、Range计算方法如式(21)—式(24)所示。

(21)

(22)

(23)

Range=max(ηZ)-min(ηZ)

(24)

式(21)—式(24)中:K为实验仿真次数;ηZ(z=[MSE,MAPE])为每次仿真实验输出的误差结果。

4.2 实验数据

实验选取水下聚能装药的5个药柱长径比(l/d)、6个相对轴向距离(h/d)和6个相对径向距离(r/d),弹药结构数据共5×6×6=180组,聚能装药数据如表2所示。

表2 聚能装药部分数据Table 2 Partial data of shaped charge

由AUTODYN软件仿真计算的聚能装药峰值超压部分原始数据如表3所示。

表3 原始数据Table 3 Raw data

梅森旋转算法随机排序后部分数据如表4所示。

表4 随机排序后部分数据Table 4 Partial data after random sorting

4.3 实验参数设置

表5 隐含层节点实验结果Table 5 Experimental results of hidden layer nodes

BP神经网络的训练迭代次数为1 000,学习率lr= 0.1,期望误差ε=0.001。隐含层激活函数:“tansig”,输出层激活函数:“purelin”,训练函数:“trainlm”。神经网络权值和阈值参数的维数为56,设计每个参数随机分配20个值,值在[-1,1]。蚂蚁数量Q=20,ρmax=0.9,ρmin=0.1。信息素初始值C= 1,最大迭代次数为N=200,其中前N1=50次迭代采用纯信息素增长策略,之后采用双曲线动态自适应调整挥发系数策略。

4.4 实验结果分析

为了验证算法的有效性,从精度和速度2个方面来评价算法,对8种智能算法分别运行500次仿真实验结果求平均值。如表6所示,DACO-BP算法的MAE、MSE、RMSE、MAPE分别为8.63×107、2.73×1016、1.46×108、19.09,分别比BP算法低44.7%、71.0%、46.7%、42.8%,比ACO-BP算法低3.7%、54.4%、6.4%、10.1%。在8种智能优化算法中,DACO-BP算法的精度最高。DACO-BP算法的拟合优度R2的值为0.971 9,均高于其他7种算法,模型拟合效果最优。在运行时间方面,DACO-BP时间为16.530 s,与ACO-BP算法时间相差不大,比BP算法慢94.1%。DACO-BP算法提升了ACO-BP算法的精度,但与BP算法相比,速度不具有优势。

表6 算法有效性仿真实验结果Table 6 Simulation results of algorithm effectiveness

为了验证算法的稳定性,分别对BP算法、ACO-BP算法、DACO-BP算法的MSE、MAPE获取其均值、方差、标准差和极差并进行稳定性对比实验。如表7所示,DACO-BP的MSE均值为2.73×1016,方差为1.37×1033、标准差为3.70×1016、极差为4.52×1017,分别比BP算法低71.0%、89.0%、66.7%、42.0%,分别比ACO-BP算法低54.4%、99.7%、94.7%、97.1%。DACO-BP的MAPE均值为19.09,方差为49.91,标准差为7.06、极差为114.55,分别比BP算法低42.8%、85.1%、61.5%、14.6%,分别比ACO-BP算法低10.1%、94.7%、77.0%、82.8%。DACO-BP算法的4个稳定性指标与BP算法、ACO-BP算法相比均显著减小,稳定性较优。

表7 算法稳定性仿真实验结果Table 7 Simulation results of algorithm stability

为了进一步验证算法的可信性,从测试集中挑选出符合水下爆炸峰值超压Cole经验公式条件的4组数据,将Cole经验公式计算的峰值超压值与DACO-BP模型预测的峰值超压值进行对比实验。如表8所示,Er为Cole经验公式计算的峰值超压值与DACO-BP模型预测的峰值超压值的相对误差。实验结果显示,4组样本数据的相对误差均小于13.84%,DACO-BP模型预测的峰值超压是可信的。

表8 算法可信性实验结果Table 8 Experiment results of algorithm credibility

5 结论

本文研究了水下聚能装药结构参数与峰值超压之间的非线性关系。采用AUTODYN数值仿真软件,获取不同长径比装药的沿轴向与径向坐标分布的冲击波峰值超压数据。基于装药结构参数得到水下聚能装药峰值超压的预测模型。利用梅森旋转算法对数据进行随机排序,提升模型的泛化性能。采用BP神经网络挖掘了峰值超压数值与装药药柱长径比、相对轴向距离、相对径向距离等结构参数之间的多变量非线性关系。构建动态自适应蚁群算法DACO解决了传统蚁群算法易陷入局部最优解和收敛速度慢的问题。设计了DACO-BP算法对水下聚能装药峰值超压进行智能预测。实验结果显示,DACO-BP算法在有效性实验、稳定性实验和可信性实验中获得较好的效果。DACO-BP的水下聚能装药峰值超压预测模型的提出,为复杂的聚能战斗部峰值超压预测提供了有效的算法与理论依据。