基于Transformer的三维模型小样本识别方法

王 辉，李建红

（石家庄铁道大学 信息科学与技术学院，石家庄 050043）

0 引言

与传统的机器学习不同，小样本学习［1-4］可利用少量数据有效识别全新的类别，不是为了让机器成功识别训练集中的数据，然后泛化到测试集，而是学会区分样本之间的差异。小样本学习有助于降低数据集的收集和标注成本，现已广泛用于人脸识别［5］、供电量预测［6］及医学应用［7-8］等领域。

目前，小样本识别的研究主要基于二维图像［9-12］。相较于二维图像，三维（Three-Dimensional，3D）模型含有丰富的空间信息，能直观表示真实场景的物体。随着三维扫描技术的发展，三维模型逐渐增多，并且在机器人导航［13］、自动驾驶［14］及虚拟现实［15］等领域得到了广泛应用；但是，三维模型的小样本识别工作仍然处于起步阶段，双元学习模型［16］利用两层长短期记忆（Dual-Long Short-Term Memory，LSTM）网络获取短期和长期知识实现对查询样本的分类，然而识别效果并不理想。为此，本文提出基于Transformer 的三维模型小样本识别方法（Few Shot Transformer，FST）。

首先，将支持与查询样本输入到点云神经网络，提取三维模型的特征向量；其次，将支持样本的特征向量输入到Transformer 模块，提取注意力特征；最后，将注意力特征与查询样本的特征向量输入到余弦相似性网络，得到相似性分数。实验结果表明，在数据集ModelNet 40［17］和ShapeNet Core［18］上，本文方法的识别效果均优于对比方法。本文的主要工作如下：

1）提出了基于Transformer 的三维模型小样本识别方法。首先，用PointNet++［19］提取特征信息；其次，利用Transformer得到注意力特征；此外，用余弦相似性网络计算关系分数。

2）在三维数据集ModelNet 40 和ShapeNet Core 上进行了大量实验，结果验证了本文方法的有效性。为验证本文方法的泛化能力，分别将ModelNet 40 和ShapeNet Core 数据集作为训练和测试集，同样得到了较好的实验结果。

1 相关工作

1.1 小样本学习

元学习利用学过的知识指导新任务的完成，使得神经网络像人类一样具有学会学习的能力［20-22］。小样本识别任务基于元学习算法实现，根据所采用方法的不同，分成基于模型微调、生成模型、图神经网络及度量学习的方法。

1.1.1 模型微调

针对数据集调整全连接或最后几层网络的参数即为模型微调的方法。文献［23］中提出在训练和测试过程中采用不同的学习率，并且使用自适应的梯度优化器，当训练和测试集差异较大时调节整个网络参数。Giadris 等［24］将正则化应用于小样本学习算法，在更新参数时利用正则化损失约束，对不同的任务采用相同的参数。动态小样本学习算法［25］利用图神经网络生成全新类别对应的权重向量，根据在训练集上得到的模型更新测试集的参数，充分利用节点间的联系，实现向量的重构和更新。

该类方法较为简单，并且适用于训练和测试集相似的数据，但在真实的应用场景中，测试和训练集往往存在差异，所以采用模型微调的方法并不能达到理想的识别效果。

1.1.2 生成模型

利用生成器扩充样本［26］，使用含有大量样本的基础类别训练特征提取网络；利用上述数据和含有少量样本的新类别共同训练分类器，达到扩充数据集的目的。基于外部记忆的算法［27］将支持样本的特征向量与该类的标签同时存储起来；然后，提取查询样本的特征向量，对比查询与支持样本的特征，得到关系度。改进的自动编码器［28］利用编码和解码器实现样本的扩充，提取同类的两个样本之间的变形信息，在解码器中利用该信息重构全新的样本。

基于生成模型的小样本识别方法简单、易于理解，但是现有的工作均基于二维图像展开研究，相比之下，三维模型具有复杂的拓扑结构，无法利用该类方法扩充数据。

1.1.3 图神经网络

将二维图像作为图卷积神经网络（Graph Convolutional Network，GCN）中的节点进行分类［29］，将标签与图像的特征向量拼接输入GCN 构建边；然后，更新节点和边向量，计算查询样本的分类概率。分布传播图网络（Distribution Propagation Graph Network，DPGN）［30］使用两个图神经网络实现小样本，其中一个图描述样本，利用节点之间的关系得到样本间的分布图，两个图将样本与分布的关系循环传播，有效实现小样本分类。与模型微调、生成模型以及度量学习相比，采用图神经网络的小样本学习方法较少。

1.1.4 度量学习

度量学习使用距离函数计算支持与查询样本的相似性分数。匹配网络［31］用卷积神经网络提取样本的特征向量，使用全连接网络度量查询与支持样本之间的相似度。DN4（Deep Nearest Neighbor Neural Network）［32］用多个局部代替全局特征，计算查询与支持样本每个局部特征的相似度，对查询样本分类。Li 等［33］则整合支持集中所有样本的注意力特征，分别与支持和查询样本计算向量积，获得具有判别信息的特征向量，利用该信息度量学习。由于三维模型相较于二维图像的不规则性，所以对三维模型的小样本识别工作仍然很少。文献［16］中基于度量学习提出含有两层LSTM 的双元学习模型，在识别任务中获取短期和长期知识，但该方法的效果并不理想。

1.2 点云神经网络

点云神经网络是对点云表示的三维模型进行数据处理的神经网络，可用于三维模型的分类、分割和检索等任务。PointNet［34］将点云作为网络的输入对每个点均单独使用多层感知器（Multi-Layer Perceptron，MLP），通过最大池化操作获得全局特征，但是PointNet 只学习点云的全局特征，忽略了局部区域的上下文信息。PointNet++［19］在PointNet 的基础上加入多尺度信息学习局部特征，将3D 点云划分为多个区域，每个区域通过PointNet 提取局部特征，解决不同密度的点云采样分布不均问题。由于PointNet++可以更好地提取点云的局部特征，故本文采用PointNet++作为特征提取网络对点云数据提取特征信息。

1.3 关系分类器

关系分类器计算查询和支持样本的关系分数。原型网络的扩展［35］使用欧氏距离度量相似性，首先，对同类样本的特征向量求平均值，作为类原型；然后，计算查询样本与每个类原型的距离，越近代表越相似，实现对查询样本的分类。关系网络［36］将分类问题转换成两个输入样本之间的相似性问题，关系分类器中输入查询样本的特征向量，使用ReLU（Rectified Linear Unit）激活函数计算分数。关系分类器也可利用图神经网络实现，将样本的特征向量视为节点，边的权重为两个节点之间的余弦相似性，根据余弦值对节点分类［37］。

上述方法均专注于学习具有良好泛化能力的深度嵌入空间，将样本转换为可用最近邻［28，30］或线性分类器［35-37］识别的数据。以上工作均是基于二维图像展开研究，相较之下，本文将点云神经网络、Transformer 以及关系分类器有效结合，实现三维模型的小样本识别。

2 小样本识别

2.1 问题定义

小样本识别指利用少量有标签的数据训练模型，学会区分类别间的差异，然后有效识别全新的类别。首先，将查询样本输入特征提取器得到特征向量；然后，利用分类器计算概率，将查询样本分类为概率最高的类别。

训练过程从训练集中随机选取C 类，每类K 个样本，一般K ＜15，共C × K 个数据，构建支持集S =作为模型的输入，其中m =C×K；然后，从该C类数据的剩余数据中每类抽取b 个数据构成查询集Q =作为模型的预测对象，其中n=C×b，即模型需要根据C×K个数据学会区分这C个类，该任务被称为C-way K-shot 问题。xi与分别表示支持与查询样本，yi与分别表示支持和查询样本的标签。由于训练过程中随机选取不同的样本，包含不同的类别组合，这种机制使得模型学会不同任务数据的差异和相同之处。

测试过程中，采用相同方法从测试集中抽取样本构造支持集和查询集，测试集均为训练过程中未出现过的新类别，即模型未见过测试集中的数据。模型对比支持和查询样本的相似度，有效识别全新的类别数据。

2.2 基于Transformer的小样本识别

在实现小样本识别任务时，Transformer 模型用于学习查询和支持样本的空间对齐关系，或者学习支持集类别间的函数映射。与使用局部特征的CrossTransformer 网络［38］不同，为了更好地适应测试集中全新的样本，FEAT（Few-shot Embedding Adaptation with Transformer）网络［39］针对度量学习中的特征提取模块作改进，在特征提取模块中加入自适应的Transformer，有针对性地提取与任务相关的特征信息，以适应不同的分类任务，具体步骤如下。

首先，在特征提取模块中使用残差网络（Residual Network，ResNet）对支持和查询样本提取特征信息，利用线性变换得到Transformer 的Q、K、V矩阵，具体计算如式（1）所示：

然后，计算每个样本之间的相似性αqk，将αqk作为权重，与值矩阵加权求和，再与支持样本的特征加和，得到与任务相关的特征信息，计算如式（2）（3）所示：

其中：V：，k表示V矩阵中的第k列，q表示样本q，d为一个常量。

最后，在关系分类器中，FEAT 网络采用距离度量方式计算查询与支持样本之间的关系分数，实现对查询样本的分类。Ye 等［39］同样使用GCN、LSTM 代替Transformer 部分，实验结果表明，在二维图像中应用Transformer 的小样本识别，效果优于通用的度量学习方法。

3 本文方法

本文提出基于Transformer 的三维模型小样本识别方法（FST）。在小样本识别中引入Transformer 提高识别精度，整个网络分为特征提取模块、Transformer 模块以及余弦相似性网络，网络框架如图1所示。

图1 基于Transformer的三维模型小样本识别方法的框架Fig.1 Framework of few-shot recognition method of 3D models based on Transformer

3.1 特征提取

本文按照2.1 节中的定义构造支持和查询集S和Q。在特征提取模块fφ中，给定查询和支持样本和xi输入fφ，共享一套参数，得到对应的点云特征。本文fφ采用2.2 节中介绍的PointNet++对三维点云提取特征信息，网络流程如图2所示。

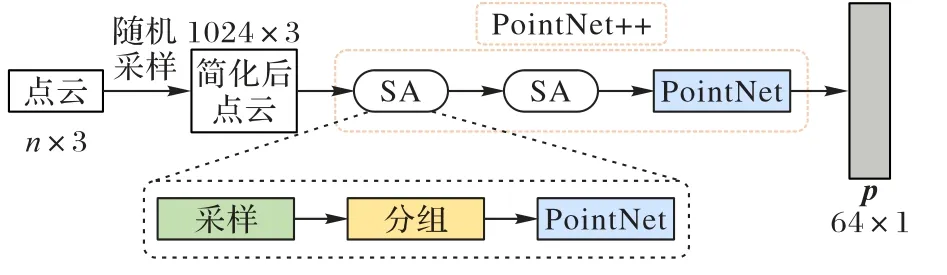
图2 特征提取模块框架Fig.2 Framework of feature extraction module

在将三维模型输入特征提取模块之前，对所有数据随机采样，每个三维模型均选取v个点，得到大小为v× 3 的点云x，3 表示三维坐标。PointNet++网络采取分层特征学习，即在小区域中使用点集抽象化（Set Abstraction，SA），其中每个SA 包括：采样、分组以及特征提取（即采用PointNet），结构为SA（中心点，半径，［mlp］）。特征提取模块的输入为v× 3，输出大小为64 × 1的特征向量p，其中，本文两次SA的参数分别设置为(512，0.2，[64，64，128])和(128，0.4，[128，128，128])。

首先，采样层的输入为v× 3，采用最远点采样法得到多个中心点；然后，在分组层以每个中心点为中心，利用球查询的方法生成若干个局部区域，每个区域最多含有512 个点；最后，将分组采样后的数据输入到PointNet 层，得到128 ×512 的局部特征。将128 × 512 同样经过采样、分组和PointNet 层，最终输出大小为64 × 1 的特征向量p。pi和的具体计算如式（4）所示：

3.2 Transformer模块

Transformer 模块包括五部分：计算矩阵、获得注意力权重、归一化处理、更新特征、得到注意力特征，该模块的输入为C×K个支持样本的特征向量pi，输出为注意力特征ψi，pi和ψi均为64 × 1 的向量，具体流程如图3 所示。

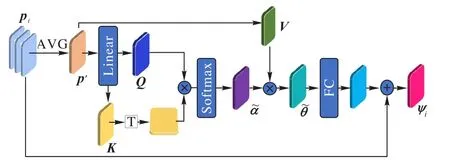
图3 Transformer模块结构Fig.3 Structure of Transformer module

首先，将C×K个点云特征pi求平均值，得到大小为64 ×1 的向量p′，对p′转换空间特征，得到查询矩阵、键矩阵以及值矩阵；其次，将p′线性变换，与值矩阵计算点积，获得注意力权重α；之后，利用Softmax 函数对α进行归一化处理；然后，将α与值矩阵相乘，得到更新后的注意力权重；最后，将经过全连接层，与pi求和，输出支持样本xi的注意力特征ψi。

将C×K个支持样本输入PointNet++提取点云特征，输出特征矩阵[C×K，64]，即每个支持样本的点云特征pi大小为64 × 1。输入Transformer 网络中，首先，计算C×K个pi的平均值p′，将p′通过线性变换得到Transformer 的查询、键以及值矩阵，计算如式（5）所示：

其中：WQ′、WK′和WV′为线性变换的权重；Q′、K′和V′分别表示查询、键和值矩阵，均为[C×K，64]的矩阵。

其次，根据式（6）计算注意力权重，将p′与WQ′相乘进行线性变换，之后与键矩阵K′计算点积，得到大小为64 × 1 的注意力权重α。将α通过Softmax 层进行归一化处理，得到注意力图α～，计算如式（7）所示：

其中，WFC表示全连接层的映射权重；τ表示进一步变换，本文采用归一化实现。

3.3 余弦相似性网络

其中：ri，j为0～1 的数值，值越大表示查询与支持样本越相似；cos(·，·)表示对输入的两个向量计算数积；ψi和均为64 维的特征向量；‖ · ‖表示对向量计算L2范数。

3.4 损失函数

借鉴文献［39］中提出的损失函数，本文损失L包括两部分：预测损失Lprec和对比损失Lcontra，每种损失具有不同的权值比例λ，计算见式（12）：

Lprec为支持样本计算注意力特征时产生的损失，用于衡量查询样本的预测和真实标签。将pi输入Transformer 计算注意力特征ψi，ψi和输入余弦相似性网络得到ri，j，ri，j经过Softmax 层得到查询样本的预测标签y^，该过程会得到预测损失，计算如式（13）所示：

其中：yd和分别表示输入样本的真实和预测标签，C×K和C×b为支持和查询样本的个数。

3.5 算法描述

本文在传统小样本识别结构中加入Transformer 网络，提取与任务相关的特征信息构成“特征提取+Transformer+关系分类”的结构，基于Transformer 的三维模型小样本识别方法如算法1 所示。

算法1 基于Transformer 的三维模型小样本识别过程。

首先，在训练集中随机选取支持和查询集，将支持和查询样本xi和输入到点云神经网络中，得到点云特征pi和然后，在Transformer 模块中输入pi，输出注意力特征；最后，余弦相似性网络计算和ψi的余弦值，越大表示越相似。

测试与训练集中不存在相同的类别数据，所以在测试过程中，从测试集抽取全新的类别，构造支持和查询集，同样经过特征提取、Transformer模块和余弦相似性网络输出关系分数。

4 实验与结果分析

本文实验在处理器为Intel Xeon Silver 4114 CPU、GPU 为16 GB NVIDIA Quadro 的图形工作站上运行，使用的开源深度学习框架为PyTorch 1.13.0，开发环境为Pycharm-2019，代码均采用Python 语言完成。

4.1 数据集

ModelNet 40 数据集［17］涵盖飞机、吉他、电脑、椅子以及楼梯等40 类物体，共12 311 个3D 模型，被广泛用于形状分类和分割，图4 为ModelNet 40 的部分模型可视化。

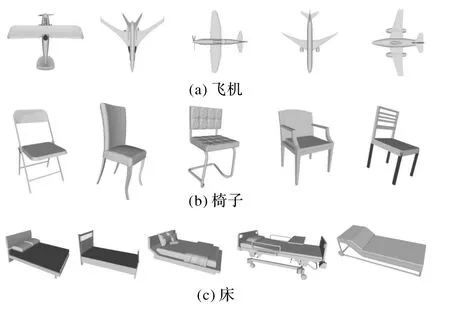
图4 ModelNet 40数据集的部分模型可视化Fig.4 Visualization of some models in ModelNet 40 dataset

ShapeNet Core 是ShapeNet 数据集［18］的一个子集，包括相机、头盔、电话以及打印机等55 类物体，共19 313 个3D 模型，本文使用ShapeNet Core 的v2版本，图5为ShapeNet Core.v2 中的部分模型可视化。

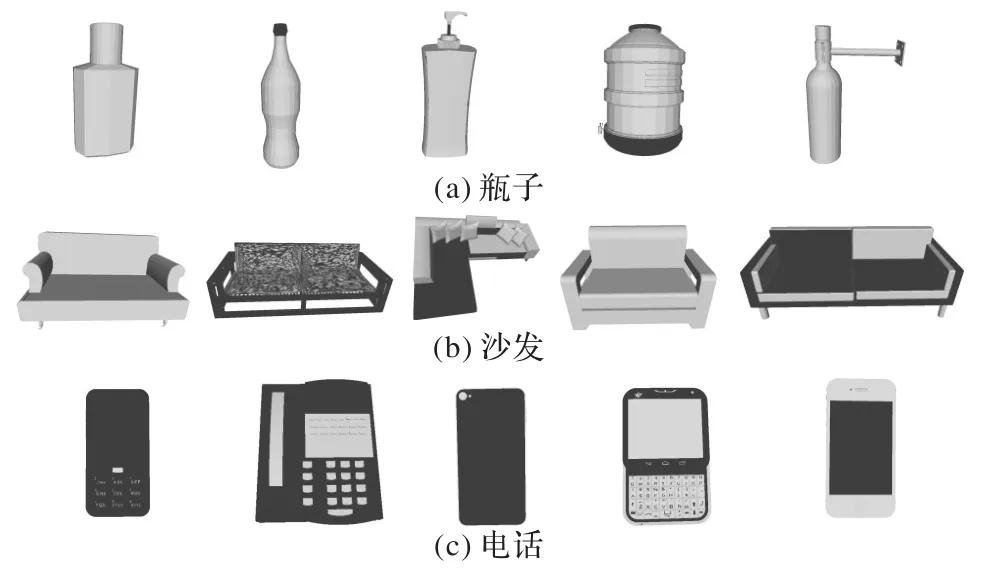
图5 ShapeNet Core数据集的部分模型可视化Fig.5 Visualization of some models in ShapeNet Core dataset

ShapeNet Core_normal 数据集含有16 类物体，共16 881个3D 模型，每个模型包含2 000 多个点。该数据集的每个类别含有不同数量的模型，比如桌子含有5 263 个模型，而耳机只有69 个。

ModelNet 40 和ShapeNet Core 均为三维网格数据集，在将模型输入网络之前，需要对数据预处理。本文中对每个三维模型随机采样v个点，然后输入PointNet++，获取特征向量。

4.2 实验细节

本文在三维点云模型输入网络前，随机采样v个点。训练时，学习率的初始值设置为0.000 1，将随机梯度下降（Stochastic Gradient Descent，SGD）中的重量衰减和动量分别设置为5E-4 和0.9。该方法每个周期训练100 次，共迭代20个周期。

本文按照目前大多数的小样本识别工作所采用的标准设置，分别进行3-way、5-way 以及7-way 的小样本识别实验。在训练过程中，除K个支持样本外，每类会随机选取b个查询样本，在C-way 1-shot 的实验中设置b=5，在C-way 5-shot 的实验中设置b=3。

本文遵循文献［16］中的分割比例，对于ModelNet 40 和ShapeNet Core 数据集，均选取30%的类别为测试集，其余类别为训练集。在训练时，从训练集中随机选取C类，测试时则从测试集中随机选取全新的C类数据。进行C-wayK-shot实验时，本文方法每次均随机选取(C×b+C×K)个三维模型，输入到点云神经网络。测试时，则从测试集中随机选取全新的C类数据。

4.3 实验结果与分析

4.3.1 模型点数选择

对数据 集ModelNet 40、ShapeNet Core.v2 和ShapeNet Core_normal 进行采样点的对比实验，将不同点数的模型输入网络，分别对比测试的识别准确率，验证该方法的鲁棒性。含有不同点数的模型如图6 所示，此处以ShapeNet Core_normal 数据集中的飞机类别为例。

图6 不同点数的点云模型Fig.6 Point cloud models with different numbers of points

分别输入256、512、1 024 和2 048 个点的ModelNet 40、ShapeNet Core.v2 和ShapeNet Core_normal 数据集，进 行5-way 1-shot 实验，测试结果如图7 所示。由图7 可知，ShapeNet Core.v2 随着采样点数的增加，识别准确率逐渐上升，在1 024 点时取到最高值；ModelNet 40 不同采样点的准确率并无大幅变动；与之不同，ShapeNet Core_normal 数据集随着输入点数的增加，准确率逐渐下降。

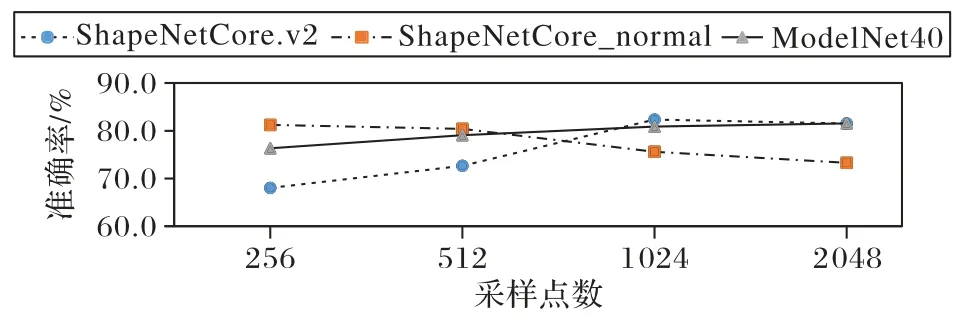
图7 不同采样点数的预测准确率变化Fig.7 Prediction accuracy varying with different sampling point numbers

ModelNet 40 和ShapeNet Core.v2 数据集取1 024 个点时准确率最高；ShapeNet Core_normal 数据集取256 点时预测准确率最高。所以，本文在实验过程中，ModelNet 40、ShapeNet Core.v2 和ShapeNet Core_normal 数据集采样点分别为1 024、1 024 和256。

3-way 1-shot 和5-way 1-shot 实验的具体准确率如表1所示。

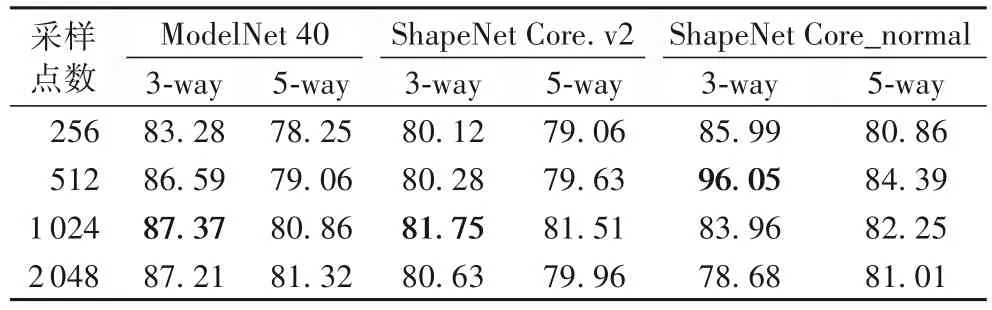
表1 不同采样点数1-shot实验的准确率 单位：%Tab.1 Accuracy of 1-shot experiments at different sampling point numbers unit：%

图8 展示了在ShapeNet Core_normal 数据集上进行不同采样点实验时，损失值随迭代次数的变化曲线。采样点数分别为256、512、1 024、2 048。由图8 可知，迭代相同次数时，在采样点为2 048 时损失值最大，收敛也最快，其次为256、512、1 024，可见采样点数不同会影响模型的识别效果。且当迭代至20 000 次时，不同采样点的损失值均趋于稳定，所以实验轮次设置为20 000。

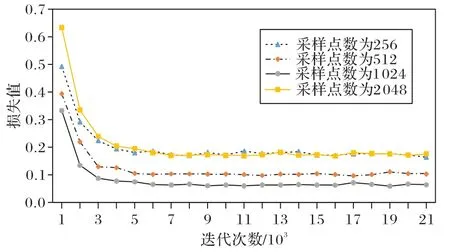
图8 不同采样点数时损失值随迭代次数变化的曲线Fig.8 Curves of loss changing with the number of iterations at different sampling point numbers

4.3.2 类别数量影响

在 ModelNet 40、ShapeNet Core.v2 和 ShapeNet Core_normal 数据集上进行3-way 和5-way 的实验，实验结果如表2 所示。由表2 可看出，实现三维模型的小样本识别任务时，预测准确率会受到类别数量的影响。

表2 本文方法在ModelNet 40和ShapeNet Core数据集上1-shot实验的准确率 单位：%Tab.2 Accuracies of the proposed method of 1-shot experiments on ModelNet 40 and ShapeNet Core datasets unit：%

当K固定时，当C值增大，预测准确率会降低，因为随类别数量增多，网络需要学习更多种类之间的异同信息，模型需在更多种类中找到与查询样本最相似的类别，预测难度随C值增大而上升，所以预测准确率降低。

在 ModelNet 40、ShapeNet Core.v2 和 ShapeNet Core_normal 数据集上进行类别数量的实验，损失值随迭代次数的变化如图9 所示，此时支持样本数量K=1，查询样本数量b=3，采样点v=1 024，迭代20 000 次。

由图9 可知，对于5-way 1-shot 以及3-way 1-shot 的实验，ShapeNet Core_normal 数据集的损失值最低，其次为ModelNet 40，而ShapeNet Core.v2 数据集的损失值最高。因为随着数据集种类的增加，损失值会相对更大，并且从模型的点云分布均匀程度分析，ShapeNet Core_normal、ModelNet 40 和ShapeNet Core.v2 数据集依次下降，所以损失值依次上升。

4.3.3 支持样本数量影响

在ModelNet 40 数据集上进行支持样本数量的消融实验，具体设置支持样本数K值为1、2、5、10，实验结果如表3所示。在5-wayK-shot 的实验中b=3。从数据集中随机选取5 类数据，然后每类随机抽取支持样本K个，查询样本3 个，所以网络的输入为(5 ×K+15)个三维模型。

表3 ModelNet 40和ShapeNet Core_normal数据集上5-way K-shot实验的准确率 单位：%Tab.3 Accuracies of 5-way K-shot experiments on ModelNet 40 and ShapeNet Core_normal datasets unit：%

如表3 所示，对三维模型进行小样本识别时，识别准确率同样会受到支持样本数量的影响。当类别数量C值固定时，随着支持样本数量K值的增大，识别准确率呈上升趋势。主要原因在于当C值固定，随K值的增大，输入到网络的支持样本数量增多，有更多的数据可用于训练网络区分不同类别之间的差异，模型更易于找到与查询样本相似的支持样本，对查询样本分类，因此识别准确率会随K值的增大而上升。相较于K=5，K=10 的准确率仅增长近0.44 和0.45 个百分点，可见当K＞5，预测效果并无很大改变，所以K的最优值为5。

4.3.4 损失权重系数的影响

本文方法的损失函数包括预测和对比损失两部分。有关对比损失的权重系数λ的取值，本文分别在ShapeNet Core_normal、ShapeNet Core.v2 和ModelNet 40 数据集上展开λ=0、0.000 1、0.01、0.1 以及λ=1 的对比实验（本文进行消融实验时，由λ=1 到λ=0.1 以及由λ=0.1 到λ=0.01，发现每次的结果并无很大变化，故并未涉及λ=0.001 的消融实验），具体结果见表4，其中，λ=0 表示忽略对比损失仅采用预测损失，损失函数的消融实验均为5-way 5-shot。

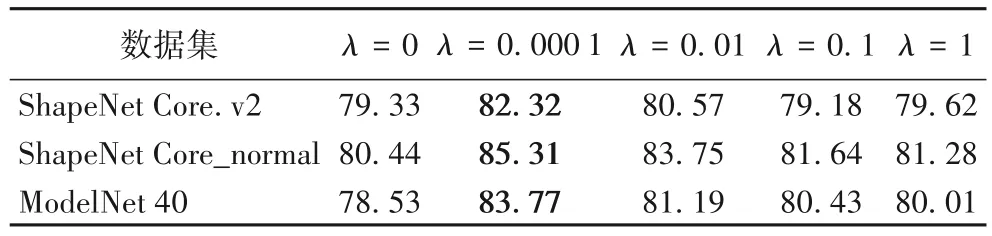
表4 不同λ值的识别准确率 单位：%Tab.4 Recognition accuracies at different λ values unit：%

分析可知，在ShapeNet Core.v2、ShapeNet Core_normal 和ModelNet 40 数据集上均为λ=0.000 1 时识别准确率达到最优，分别为82.32%、85.31%和83.77%。当λ=0 时，本文损失仅为预测损失，此时在3 个数据集上的识别准确率分别达到79.33%、80.44%、78.53%，均低于λ≠0 时的识别效果，这表明采用对比损失的重要性；当λ≠0 时，对比表中结果可知，均低于λ=0.0001 时的准确率，所以，本文所有实验中均设置λ=0.0001。

4.3.5 对比实验

参考文献［40-41］中C和K的取值，本文在5-way 10-shot、5-way 20-shot、10-way 10-shot 以及10-way 20-shot 实验上分别对比3种方法：DGCNN+cTree［40］、PointNet+cTree［40］及PointNet+Jigsaw［41］的识别准确率，具体实验结果如表5所示。

表5 不同深度学习方法在ModelNet 40数据集上的小样本识别准确率 单位：%Tab.5 Few-shot recognition accuracies of different deep learning methods on ModelNet 40 dataset unit：%

由表5 可知，本文方法在5-way 10-shot 和5-way 20-shot 的识别准确率分别为84.21%和81.53%，在10-way 10-shot 和10-way 20-shot 可达到80.32%和80.75%，识别效果均高于其他对比方法。其中，与文献［40-41］中的3 种方法中效果最好的PointNet+Jigsaw［41］相比，本文方法的准确率分别提高了17.71、12.33 和23.42、14.25 个百分点，验证了方法的有效性，说明本文方法可有效提高三维模型小样本识别的准确率。

在ModelNet 40 数据集上针对Dual-LSTM（Dual-Long Short Term Memory）、关系网络、无Transformer 网络和本文方法展开对比实验，测试结果如表6 所示。其中，将PointNet++与余弦相似性网络结合，计算关系分数，该方法记为无Transformer 网络。

表6 不同三维模型小样本识别方法在ModelNet 40数据集上的5-way准确率 单位：%Tab.6 Five-way accuracies of different few-shot recognition methods of 3D models on ModelNet 40 dataset unit：%

由表6 的实验结果可知，本文方法在ModelNet 40 数据集上进行5-way 1-shot 和5-way 5-shot 的识别实验的结果均优于其他对比方法。

无Transformer 网络的方法首先利用PointNet++对支持和查询样本提取点云特征；然后，余弦相似性网络将查询与支持样本的特征相乘，得到相似性分数。由实验结果可知，在ModelNet 40 数据集上进行5-way 1-shot 和5-way 5-shot 的实验，预测准确率分别为35.56%和36.92%，无法达到理想的识别效果。

本文将Transformer 网络用于三维模型的小样本识别，提出FST 方法，对特征信息增加注意力，得到与任务更为相近的特征信息，然后利用余弦相似性网络计算查询与支持样本的相似性分数。FST 的识别效果较好，在5-way 1-shot 的实验中识别效果比无Transformer 的方法提高了45.30 个百分点，在5-way 5-shot 的实验中提高了46.85 个百分点，这表明加入Transformer 网络可以有效提高三维模型小样本识别的准确率。

将FST 方法与Dual-LSTM 模型［16］相比，在5-way 1-shot 和5-way 5-shot 的实验中识别准确率分别提高了34.54 和21.00个百分点，验证了该方法的有效性。所以，将Transformer 应用于三维模型的小样本识别任务中，对网络增加注意力模块，可有效提升网络特征提取的能力，从而提高识别准确率。

4.3.6 结果展示

在C-wayK-shotb-query 实验的设置下，网络的输入为(C×K+C×b)个三维模型，最终输出[C×b，C×K]的分数矩阵R={ri，j}，其中矩阵中每个元素表示对应行的查询样本与对应列的支持样本之间的关系分数，将查询样本分类为该行中最大分数所对应的支持样本所属类别，图10 为本文方法的结果示例。

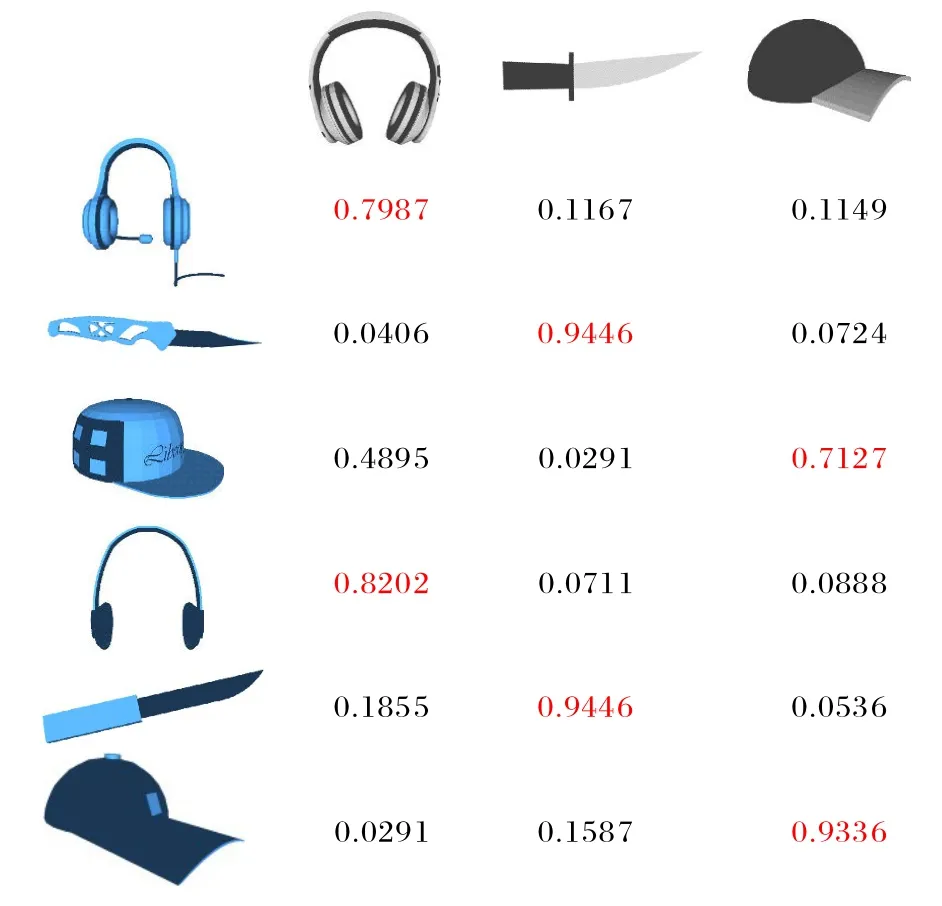
图10 关系分数矩阵Fig.10 Relation score matrix

如图10 所示，此处以3-way 1-shot 2-query 为例，计算得到［6，3］的关系矩阵，例如图10 中第1 行：支持样本为耳机、刀子、帽子，与查询样本的关系分数依次为0.798 7、0.116 7、0.114 9，所以本文方法将查询样本分类为耳机。

由于查询样本的形状不一，所以与同一支持样本的关系分数也不同。如图10 中第3、6 行，查询样本均为帽子，当支持样本固定为帽子时，与第3 和6 行中查询帽子的关系分数分别为0.712 7 和0.933 6，这是因为第2 个查询帽子与支持帽子更为相似。

1）3-way 1-shot 1-query实验结果。

以3-way 1-shot 1-query 为例对实验的结果可视化，图11中左侧1 列的模型为查询样本（虚线框内），右侧为支持样本从左到右依次按相关分数降低排列。进行实验时，网络的每次输入为6 个三维模型，其中3 个支持样本，3 个查询样本。

图11 3-way 1-shot 1-query实验结果Fig.11 Experimental results of 3-way 1-shot 1-query

图11 为3-way 1-shot 1-query 的实验结果展示，随机选取的类别为耳机、吉他、椅子。图11 中第1 行的关系分数依次为：0.857 9、0.377 5、0.476 4，所以识别查询样本与耳机为同类；第2 行为0.901 4、0.387 9、0.462 5，查询样本被识别为吉他；第3 行为0.826 5、0.497 4、0.377 5，将查询样本识别为椅子。分析可知，查询与支持样本的形状发生变化，同样两个类别的关系分数不同，所以，本文可以有效识别模型之间的差异。

2）5-way 1-shot 1-query实验结果。

进行5-way 1-shot 1-query 实验时，网络的输入为10 个三维模型，其中5 个支持样本，5 个查询样本。将10 个三维模型输入至网络，本文方法得到大小为［5，5］的关系矩阵，对每行中关系分数降序排序，即查询样本与每个支持样本的相似度排序。

在ModelNet 40 数据集上进行5-way 1-shot 1-query 实验的部分结果如图12 所示，以图12 中第1 行为例说明，当查询样本固定时，支持样本为床、书柜、吉他、键盘、玻璃柜，其关系分数依次为0.983 5、0.822 5、0.795 3、0.555 6、0.224 7，所以将查询样本分类为床。

图12 5-way 1-shot 1-query实验结果Fig.12 Experimental results of 5-way 1-shot 1-query

当两个类别存在相似之处时，如摩托车和火车，本文方法可根据对比模型之间的差异成功分类。如图12 中第3 行的花瓶与水桶均为圆形物体，在外观上相似，但与花瓶的关系分数较高，所以将查询样本识别为花瓶，可见本文方法可以正确识别形状相似的类别。

5 结语

本文提出一种针对三维点云模型的小样本识别方法，包括特征提取模块、Transformer 模块和余弦相似性网络。首先，特征提取模块采用PointNet++对三维点云模型提取特征向量；然后，将支持样本的特征向量输入Transformer 模块，得到注意力特征；最后，将支持样本的注意力特征与查询样本的点云特征利用余弦相似性网络计算关系分数。相较于现有工作，在ModelNet 40 和ShapeNet Core 数据集上，该方法均提高了三维模型小样本识别的准确率。

然而，本文方法在实验过程中仍会出现识别错误的情况，如图13 所示，查询样本为圆形椅子，却错误认为与圆形罐子最为相似。此外，本文方法局限于对点云表示的三维模型进行小样本识别，无法处理网格、体素等其他表示方法。未来考虑将本文方法扩展到三维模型的网格或体素等表示方法。

图13 失败结果示例Fig.13 Example of failure results