基于势函数的多机器人编队协调控制模型仿真

张 军,李林森,解乃军,温秀平

(1. 南京工程学院,江苏 南京 210016;2. 上海交通大学电子信息与电气工程学院,上海 闵行 200240)

1 引言

相较于工作能力有限的单机器人,多机器人编队无论是在工作能力方面,还是在工作效率方面,均表现出一定的优势,因此,多机器人编队已成为当下社会的热议话题,被广泛应用于医疗卫生、机械制造、航空航天、灾难救援、军事演练等多个领域[1,2]。然而,多机器人编队的应用存在两面性,即多机器人编队在给人类生活带来便利的同时,其编队协调能力不足也会直接导致机器人队形散乱、步调不统一,甚至产生严重的障碍物碰撞问题。为了改善该问题,国内外相关人员对多机器人编队协调控制方法展开研究。

彭滔[3]等人通过分析多机器人编队运动状态获取多机器人编队运动学特性,并利用径向基函数将多机器人编队运动学特性映射至神经网络中。经过映射的神经网络根据李雅普诺夫稳定性理论收敛网络边界,直至网络内“距离-角度”呈现自适应闭环状态,此时的神经网络已脱离未知信息描述阶段,成为描述多机器人编队打滑和不打滑状态的控制性网络,将多机器人编队相关数据输入该网络中,即可实现多机器人编队协调控制。师五喜[4]等人通过虚拟领航-跟随装置,读取多机器人编队在全局坐标系下的运动学模型,通过将模型与编队控制器结合,实现多机器人编队协调控制。吴军成[5]等人通过类鸟群模拟方法将多机器人编队置于全局坐标系中,并利用控制器协调变换编队坐标信息,实现多机器人编队协调控制。

当队形发生切换时,上述方法均存在协调控制性能较差的问题,为此,本文提出一种基于势函数的多机器人编队协调控制方法。

2 多机器人编队数学模型

多机器人编队数学模型是将单机器人视为二维平面上运动的质点,并从速度向量、位置向量和间距向量三个方面描述多机器人编队运动的虚拟模型。想要协调控制多机器人编队,首先需要建立阐述多机器人编队运动的多机器人编队数学模型[6,7]。

一致性协议[8]是Reynolds教授于1986年参考自然生态环境中群居鸟类行为特点提出的一种模态理论。该理论认为多个个体组成群体后,群体会在附加增益的作用下自发产生分离、匹配、聚合等编队效应。分离编队效应是指个体通过斥力场函数与邻近个体保持不接触、不碰撞的位置关系。匹配编队效应是指个体通过SLAM(simultaneous localization and mapping)算法[9]维持与其它个体同等运动速度,以保证群体运动的一致性。聚合编队效应是指个体根据线性引力论[10]与邻近个体保持相对距离,使群体朝向同一目标共同运动,且不会出现个体离队或掉队的问题。根据上述理论,给出斥力场函数的表达式如下

(1)

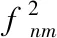
SLAM算法的表达式如下

L=y2|ko-I|-μ

(2)

式中,y2表示个体速度耗散力;ko表示匹配编队控制条件;I表示群体状态同步程度;μ表示附加增益值。

线性引力论的表达式如下

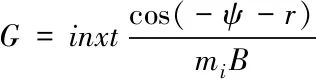
(3)

式中,ψ表示引力均值;r表示聚合编队控制条件;mi表示个体间的数据交换量;B表示负反馈比例调节因子。

将单机器人视为一致性协议中的个体,通过组织多个单机器人形成编队,实现多机器人编队数学模型的构建。多机器人编队数学模型的表达式如下

(4)

式中,Os表示多机器人编队运动学特征;∇z表示机器人间的排斥力;xo表示机器人间的吸引力;xn表示多机器人编队期望速度分量;σ2表示多机器人编队几何中心;b表示多机器人编队最大步长。

3 多机器人编队协调控制

3.1 领导者-跟随者状态

势函数又称二重势函数法[11],是Khatib教授在法国攻读博士学位期间提出的多机器人编队数学模型状态重构方法。该函数自1980年提出以来,先后被美国Stanford大学、印度国际会议列为最具影响力的机器人科技研究成果。势函数的核心思路是通过在多机器人编队数学模型中择选出一个领导型机器人,并从运动初始时刻开始要求该机器人携带六维力传感器[12]和辅助平衡轮,以达到维持编队速度分量和队形统一的目的。除领导型机器人外的其余机器人统称为跟随型机器人,这种机器人不存在数量限制,即编队容量的大小并不影响整体编队的协调控制效果。势函数择选领导型机器人并不是随机操作,而是在径向滑动和侧向滑动两种复杂环境下,根据模型内机器人双轮驱动连线与障碍物位置产生的偏离角度判断机器人是否符合择选条件。只有当偏离角度小于30度时,才能确定该机器人能够在任意工况环境下作出合理运动,且不存在与障碍物对峙的死锁[13]问题。偏离角度的计算公式如下

(5)

领导型机器人的成功择选对多机器人编队数学模型协调控制起到基础性作用。在编队尚未区分机器人属性时,各机器人间并不存在直接或间接的物理联系,而势函数的加入使模型重新审视各机器人之间的关系。领导型机器人作为编队的领导者,不仅可以通过六维力传感器向任意机器人施加作用信号或接收任意机器人的反馈信号,还可以通过辅助平衡轮在一定距离和角度内缓解编队变形趋势。跟随型机器人作为编队的跟随者,主要将领导型机器人视为轴线所在直线上持续运动的跟踪对象,并在跟踪对象的指导下完成编队需要执行的目标任务。六维力传感器发送信号的表达式如下

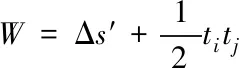
(6)

式中,Δs′表示信号波形;ti表示信号恒收敛系数;tj表示六维力传感器演化时间。

六维力传感器接收信号的表达式如下

(7)

式中,A3表示信号特征值;cosq1表示信号幅值。

辅助平衡轮要想缓解编队变形趋势,需要从距离和打滑量两方面入手,一方面,缩减两驱动轮转速不等的机器人距离,另一方面,沿编队轴线重合方向降低机器人打滑量。在势函数的协助下,多机器人编队数学模型由初始散乱状态转化为有序的领导者-跟随者状态,极大程度提升了多机器人编队协调控制的操作空间。

3.2 Backstepping控制器

想要从根本上提升多机器人编队队形稳定性和灵活变换性,实现多机器人编队协调控制,需要将处于领导者-跟随者状态的多机器人编队数学模型与Backstepping控制器[14]结合,根据控制器输出的控制策略,针对性调节多机器人编队队形参数。

Backstepping控制器是由上层SDK通信接口[15]和下层领导者-跟随者控制中心构成的双层机器人约束系统。控制器上层通过读取多机器人编队完整移动空间,将空间内障碍物坐标通过无线通信的方式记录在matlab/simulink仿真平台。障碍物坐标作为机器人虚拟位姿变换的定点坐标,只有在多机器人编队遵循指定队形参数,并跟踪领导型机器人主轨迹的前提下,才能以多机器人编队理想拓扑结构跨越定点坐标。考虑到多机器人编队数学模型既适用于纯滚动复杂环境,又适用于纯滑动复杂环境,因此,控制器上层在完成障碍物坐标记录工作后,会根据matlab/simulink仿真平台记录结果制定多机器人编队控制策略。编队理想拓扑结构的数学表达式如下

(8)

式中,ux表示编队质心加速度;λij表示多机器人间的安全距离;zx表示编队对齐规则;φij表示编队分离规则。

控制器下层是Backstepping控制器的执行层,其根据上层控制策略,从领导型机器人和跟随型机器人两方面入手,开始对多机器人编队协调控制,针对领导型机器人的协调控制主要集中在领航速度和领航方位上。根据控制策略的期望速度调整领航速度,避免领导型机器人脱离编队匹配位置,从而导致编队在短时间内发生速度控制量时变。控制策略期望速度的数学表达式如下

γ=ω(xref×yref)

(9)

式中,ω表示编队统一速度;xref表示速度分布控制律;yref表示速度协调策略。

领航速度的调节公式如下

H=rirjcos(rθ)

(10)

式中,ri表示领航线速度阈值;rj表示领航角速度阈值;rθ表示领航速度调节常量。

根据控制策略的期望方位调整领航方位,避免领导型机器人的运动轨迹偏离目标运动轨迹。控制策略期望方位的数学表达式如下

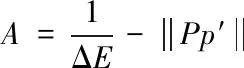
(11)

式中,ΔE表示方位分布控制律;Pp′表示方位协调策略。

领航方位的调节公式如下

E′=v11

(12)

式中,v1表示下步方位信息;1表示多机器人编队角度裕量。

针对跟随型机器人的协调控制主要集中在跟随关系的全局一致性上,根据控制策略的期望一致性加强跟随关系的全局一致性,使多机器人编队无论在队形变换方面,还是在运动速度方面,均能够高度协调。

综上所述,根据协调控制器输出的控制策略,即可实现多机器人编队的协调控制。

4 实验与分析

为了验证基于势函数的多机器人编队协调控制方法仿真的整体有效性,需要对其测试。

4.1 实验条件设置

实验中所用机器人型号为IRB6700-150/3.2,轴数为6轴,有效载荷为150kg,重复定位精度为±0.1mm。选取5个该型号的机器人作为实验对象,进行编队协调控制。采用上文提到的matlab/simulink仿真平台对机器人的运动轨迹进行采集,获取多机器人运动的队形变化情况,图1为仿真界面输出结果。

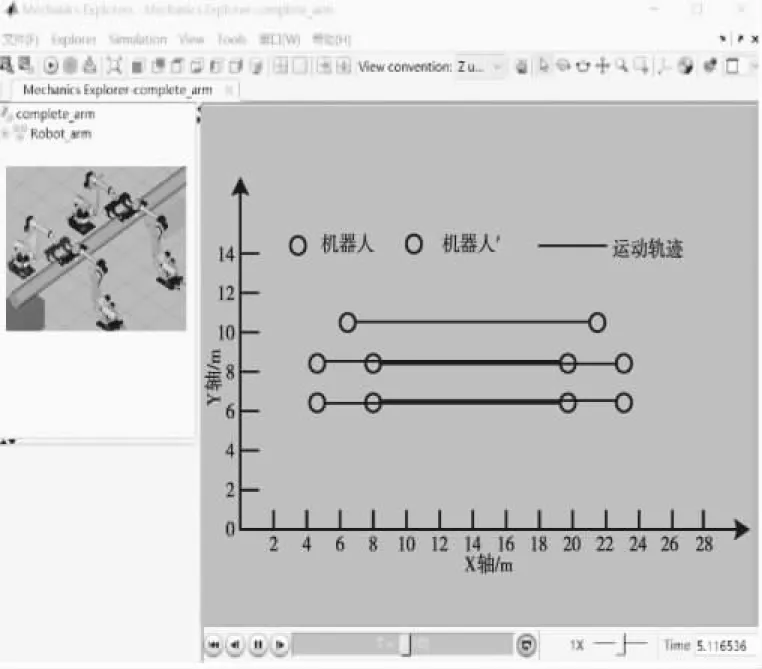
图1 仿真实验结果输出图

在上述实验环境下,将文献[3]方法、文献[4]方法、文献[5]方法和所提方法进行对比,得出相关结论。

4.2 控制效果验证

随机选择一组包含5个机器人的多机器人编队作为验证算法队形保持能力的试验对象。将多机器人编队置于直角坐标系中,其初始位置及初始队形如下图2所示。

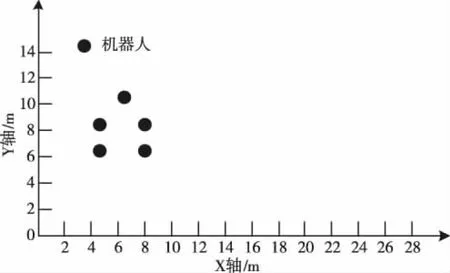
图2 多机器人编队初始位置及初始队形

分别采用所提方法、文献[3]方法和文献[4]方法协调控制多机器人编队,使其从初始位置移动一段距离。通过观察不同方法控制下,编队运动轨迹和队形保持情况,判断不同方法对多机器人编队的协调控制性能。不同方法控制下,编队运动轨迹和队形保持情况如下图3所示。

图3 不同方法控制下编队运动轨迹和队形保持情况

如上图3可见,采用所提方法协调控制多机器人编队时,其编队运动轨迹较短,且编队内各机器人步调统一,队形保持情况较好。而采用文献[3]方法和文献[4]方法协调控制多机器人编队时,二者编队运动轨迹散乱,且编队内各机器人步调不统一,队形保持情况较差。经上述对比,可知所提方法对多机器人编队的协调控制能力明显优于传统方法。因为所提方法将多机器人编队数学模型与Backstepping控制器结合,根据控制器输出的控制策略实现多机器人编队协调控制,这样获取的控制结果可信度更高、效果更好。

为了进一步验证所提方法的实用性,现规定多机器人编队每间隔1min切换一次指定队形(指定队形包括直线形和三角形)。分别采用所提方法、文献[4]方法和文献[5]方法协调控制多机器人编队,通过观察不同方法控制下编队队形切换及保持情况,判断不同方法对多机器人编队的协调控制能力。不同方法控制下编队队形切换及保持情况如下图4所示。

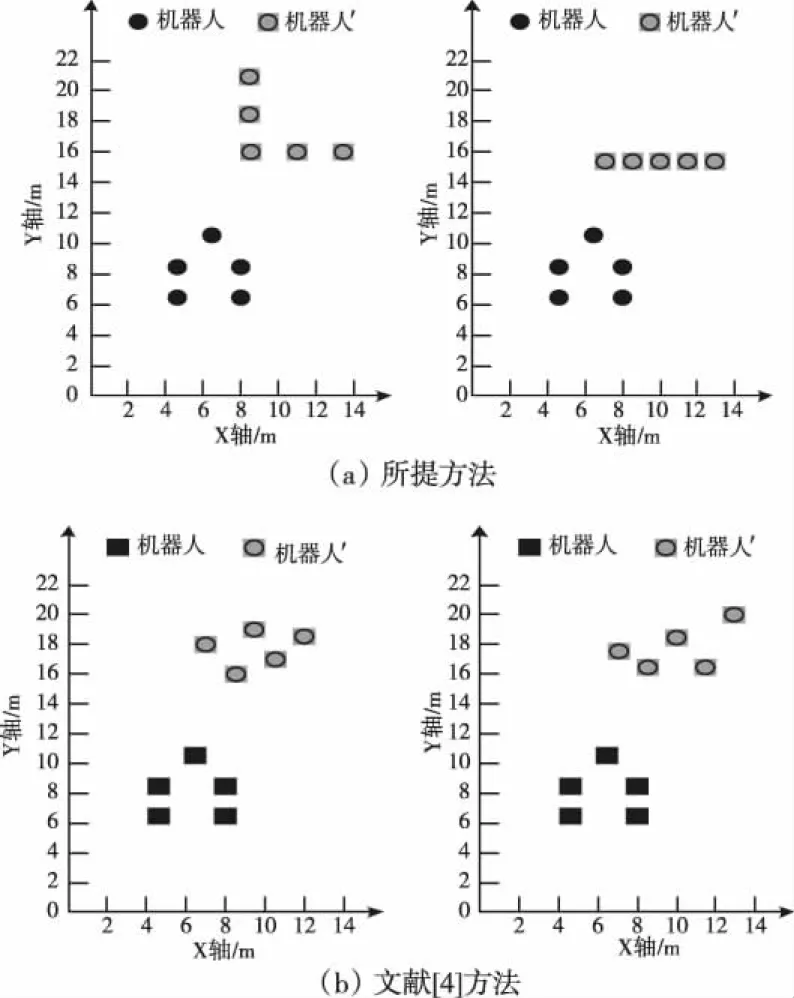
图4 不同方法控制下编队队形切换及保持情况

如上图4可见,在队形保持方面,所提方法、文献[4]方法和文献[5]方法的控制效果均较好,而在队形切换控制中,所提方法的队形切换及保持效果更好,没有出现。采用文献[4]方法和文献[5]方法协调控制多机器人编队,二者队形切换及保持效果不佳。经上述对比,进一步验证了所提方法的实用性。

5 结束语

多机器人编队作为融合多项跨专业学科的先进技术,因其优越的命令执行能力,被广泛应用于巡逻、搜救、侦察等领域。为了提高多机器人编队控制效果,提出基于势函数的多机器人编队协调控制方法。仿真实验结果表明,该方法不仅能够对多机器人编队进行有效保持,而且具有良好的队形切换控制效果。如何在保证多机器人协调控制性能的同时,对多机器人协调控制过程实时监控,是研究人员下一步工作的重点。