Morozov偏差原则在具有凸罚项的非线性不适定问题中的应用

阳科全，丁 亮

（东北林业大学）

0 引言

该文考虑求解具有如式（1）形式的不适定算子方程

其中x ∈X，A：X →Y表示自反Banach空间X，Y之间的非线性算子.‖·‖X，‖·‖Y分别表示X，Y空间中的范数.在实际应用中，精确数据y往往不能预先得到，从而采用测量数据yδ替代精确数据y，y与yδ满足‖y－yδ‖Y≤δ，其中δ ≥0为噪声水平，yδ∈Y.

在实际生活中，很多数学物理问题可以归结为算子方程（1），例如医学成像问题及逆散射问题等.算子方程（1）往往是不适定的，因此需要正则化技术来稳定算子的反演，更多细节可以详见参考文献［1］.其中一种常见方法是Tikhonov正则化［2］，这种方法的原理是寻找以下变分问题的解作为（1）的近似解

其中α ＞0是正则化参数，Ψ（x）是正则化项或称罚项.解决以上变分问题的关键是选择一个合适的正则化参数α.一般来说，确定α 有两种原则：一个是先验参数选择原则，另一个是后验参数选择原则.对于先验原则，α由α ＝O（δ）确定，例如固定c ＞0，α ＝cδ.但是如何找到最优的c却是十分困难的.作为一种后验原则，MDP（Morozov偏差原则）是最常用的确定正则化参数α的方法，这种方法已经有大量研究成果.该方法确定正则化参数α ＝α（δ，yδ），使得

其中τ ＞1，xδα为（2）的一个解.如果Jδα（x）的最小值解是唯一的，文献［3－4］已经证明至少存在一个正则化参数α使得（3）成立.

对于线性不适定问题，MDP 的理论分析可以追溯到1966年［5］.在文献［6－8］中，已经提出几种数值算法用于计算经典的二次Tikhonov正则化的正则化参数α.随后，MDP 的理论分析推广到更一般的凸正则化.在文献［7］中，MDP应用于具有一般凸的Tikhonov正则化中.在文献［9］中，提出了两种具有一般凸惩罚项的非光滑Tikhonov正则化的MDP 迭代参数选择方法.

对于非线性不适定问题，由于最小值解可能存在多个，导致处理线性不适定问题的方法不能直接推广到非线性不适定问题中.对于非线性不适定算子方程，MDP 的一个缺点是，可能不存在满足（3）式的正则化参数α，从而需要特殊的方法来分析由MDP 确定的正则化参数α 的存在性.对于经典的Tikhonov正则化，文献［10］表明对非线性算子F和算子方程F（x）＝y 的最小值解xδα加一些限制，一定能找到正则化参数α使得δ ≤‖F（x）－yδ‖≤τδ（τ ＞1）成立，并给出了相应的收敛速度.对于一般的凸惩罚项，文献［4］在一定条件下证明了α 的存在性，并且表明，对于该参数选择原则，当噪声水平δ →0 时，α →0以及δq／α →0（q ≥1）.在文献［3］中，作者使用变分不等式研究了收敛速度，其中正则化参数由MDP 确定.文献［3］给出了Tikhonov 正则化中最小值解的唯一性与Morozov 偏差原则之间的联系.

当非线性不适定问题中罚项为一般凸时，MDP 在理论分析上还尚有许多亟待解决的问题，尤其是正则化参数的存在性问题.该文假设算子A满足如下非线性条件，存在常数γ ＞0使得

在条件（4）成立的前提下，建立非线性不适定问题中罚项为一般凸时的偏差原则，证明至少存在一个正则化参数α使得

此外，该文分析了由式（5）确定的正则化解的存在性，收敛性，以及正则化解的收敛速度.

1 预备知识

定义2定义x†∈X为Jδα（x）的最小Ψ解（又称Ψ（x）最小值解），如果x†满足：

（i）A（x†）＝y.

条件1该文假设非线性算子A和测量数据yδ满足下列条件：

（i）A：X →Y是Fréchet可导的.

（iii）存在常数γ ＞0使得

（iv）存在τ ＞1，使得

对于条件1（iii）中式（6）已经被广泛使用，如文献［1，11，12］.它被其他研究人员所采用的使用形式为‖A′（x1）（x2－x1）‖Y≤（1 ＋γ）‖A（x2）－A（x1）‖Y.对于式（7），由于实际应用中几乎不可能从观测数据中反演出与观测数据同阶的精确解，如果δ ≤‖A（0）－ yδ‖Y≤τδ，那么0通常可被视作是正则化解xδα的良好估计，所以在该文中假设‖A（0）－ yδ‖Y＞τδ.

条件2假设Ψ（x）满足如下条件：

（i）凸性：∀x，y ∈X，t ∈［0，1］，有Ψ（tx ＋（1－t）y）≤tΨ（x）＋（1－t）Ψ（y）.

（ii）强制性：若‖x‖X→∞，则Ψ（x）→∞.

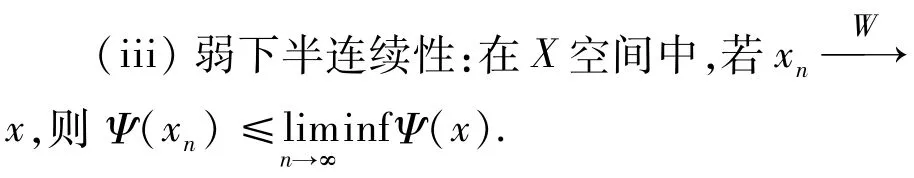
（iv）Radon－Riesz性质：在X空间中若

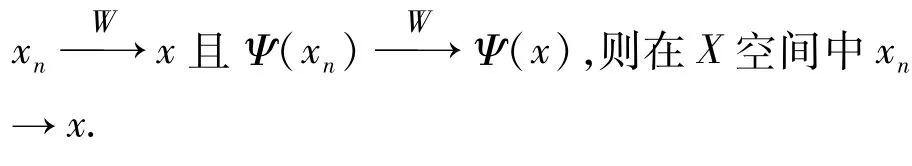
2 正则化参数的存在性

引理2假设τδ ＜‖A（0）－ yδ‖Y，对于正则化参数α ＞0，若没有最小值解xδα1，xδα2∈Lδα使得

成立，则一定存在α ＝α（δ，yδ）＞0 以及xδα∈Lδα，使得δ ≤‖A（xδα）－ yδ‖≤τδ 成立.

接下来以引理3的形式给出一阶优化条件，详细证明参见文献［13］.证明在τ满足某些条件下，存在正则化参数α 使得MDP 成立.

因此

从而

结合条件1（iii）有

此外

结合式（9），（10）可以得到

从而

由不等式（12）可以得到‖A（x2）－yδ‖Y≤（2γ ＋3）δ，引理得证.

由引理2和引理4可以得到定理2.

定理2假设条件1满足，则存在一个正则化参数α 使得

证明假设条件1满足.

3 正则解的收敛性和收敛速度

这一节将在式（13）下证明正则化方法的适定性，正则解的收敛性以及收敛速度.沿着标准二次Tikhonov正则化［2］的思路证明正则化解xδα收敛到Jδα（x）最小值解以及讨论xδα的收敛速度，收敛速度与参考文献［14］中的不同，因为正则化参数α 现在由式（13）决定.

定理3（收敛性）若为（x）的一个最

证明定义由xn的定义可知，

结合式（14）则有

因此序列｛Ψ（xn）｝是有界的.定义cδn＝max｛τδn，（3 ＋2γ）δn｝，那么有δn→0时，cδn→0.又因为

另一方面，由式（14）可知

因为Ψ（xn）是有界的，所以存在一个x*∈X以及{xn}的一个子序列，仍记为{xn}，使得在X中结合式（16）可以得到：

因此Ax*＝y.由条件2（iii）有

定义4∂Ψ表示Ψ的次梯度.对于x，z ∈X，Ψ的Bregman距离定义为：

其中

上述式（20）表示ξ ∈∂Ψ（z）时Ψ的Bregman距离.

Burger 和Osher首先证明Tikhonov 正则化中的算子为线性算子，罚项为凸时在Bregman距离下的收敛速度［15］，随后Resmerita 和Scherzer将研究的结果推广到了非线性正则化中［16］.Stephan和Ronny在上述的研究基础上加入了一些非线性条件，证明了由MDP 确定的正则解的收敛速度为O（δ）［17］.下面以条件3的形式给出.

条件3对任意的x†，存在w ∈Y*，使得

对任意的w ∈Y*且w满足式（19），ξ ∈∂Ψ（x†）定义为：

此外，由条件1（iii）可推出：

对任意的x，z ∈X，存在γ ＞0，使得

定理4（收敛速度）算子A以及罚项Ψ满足条件1、2、3.假设正则化参数α 由偏差原则

确定，这里C ＝max｛τ，3 ＋2γ｝，那么

证明由的定义可得

从而Ψ（xδα）≤Ψ（x†）.

则收敛速度为O（δ）.

4 结论

该文在一般源条件下引入已经广泛应用的非线性条件（5），分析具有一般凸惩罚项的非线性不适定算子方程A（x）＝y 的正则化参数的存在性.在Morozov偏差原则δ ≤‖A（xδα）－ yδ‖Y≤max｛τδ，（3 ＋2γ）δ｝下，证明正则化参数α的存在性.此外，证明了正则化解的收敛性.在Bregman距离下证明了正则化解的收敛速度为O（δ）.