带有顶点权重约束的图划分问题研究*

丁玉婉，刘红卫，王 婷，王晓瑜，游海龙

（西安电子科技大学）

0 引言

图划分问题是经典的组合优化问题，其目标是将一个具有边权值的图的顶点按照约束条件分成k个不相交的子集，同时最小化集合间的互连边权之和，该问题被广泛应用于并行计算处理［1］，图像处理［2］，超大规模集成电路设计［3］，移动无线通信［4］等众多领域.

自20世纪60年代以来，国内外学者不断对图划分问题进行研究，提出了许多性能较好的图划分算法.文献［5］提出了一种谱方法用于求解图的二划分问题，其基本思想是利用图矩阵的第二大特征值和特征向量来实现图划分.文献［6］提出了一类KL算法，这是一种典型的启发式算法，该算法先将图随机二分，再高效地选择收益最高的点进行交换.文献［7］在KL 算法的基础上进行改进提出了FM 算法，该算法采用单点移动策略且引入了桶列表数据结构，降低了算法的时间复杂度.智能优化算法，如遗传算法［8］、禁忌搜索算法［9］等，也被用于求解图划分问题.一些学者还用整数规划的方法来求解图划分问题，文献［10］描述了连通图上的整数规划公式.文献［11］提出了一种使用分支定界框架来求解最小图二划分的精确组合算法.文献［12］给出了多约束图划分问题的两个整数规划公式，并提出了一种基于分支定界和切平面的精确算法.

半定规划是凸优化中一个相对较新的子领域，由于它在运筹学和组合优化问题中有非常成功的应用，因此许多学者利用半定规划松弛来求解图划分问题.文献［13］引入了几个组合优化问题的半定规划松弛，包括图划分和最大割问题.文献［14］提出了一般图划分问题的一种新的半定规划松弛方法.文献［15］介绍了一种基于分支定界法求解图划分问题的精确算法，且一系列数值实验表明，半定规划方法通常会导致更紧的下界.文献［16］用一种基于半定规划松弛的分支定界法来计算图划分问题的全局最优解.文献［17］基于矩阵的提升推导出了一种新的用于图划分的半定规划松弛，并从理论和数值两方面与其他半定规划松弛进行了比较.

近年来一些学者对带有顶点权重约束的图划分问题展开了研究，其中最著名的是背包约束下的图划分问题（GPKC）.文献［18］结合严格的线性规划松弛方法和启发式方法建立了GPKC问题的上界.文献［19］将GPKC 问题的0，1整数模型转化为半定规划松弛模型，并利用扩展的乘子交替方向法（eADMM）来求解该模型，并利用启发式算法得到了GPKC 问题的较好的下界.注意到文献［19］中提到，对于大规模实例，内点法并不适用于求解其半定规划松弛模型，并在数值实验部分进一步说明了内点法求解器Mosek［20］由于内存需求不足而无法求解顶点数超过300的大规模实例.

由于内点法是求解半定规划最经典有效的算法，因此，基于文献［19］的思想考虑使用改良的内点算法求解半定规划松弛问题，以进一步优化图划分求解算法.由于图的k划分问题能通过递归的二划分进行求解，而该策略的性能主要取决于二划分算法的选择，因此该文主要对k ＝2时的图划分问题展开深入研究，并进一步研究了带有顶点权重约束的图划分问题.受文献［19］的启发，该文首先基于矩阵的提升将原问题的－1，1整数规划模型转化为一个新的半定规划松弛模型，并使用改进的半定规划内点法进行模型求解，其中给出了具体的初始点选取策略和步长选取策略.随后利用改进的随机超平面舍入算法和文献［19］中提出的2opt启发式算法得到原问题的近似最优解.数值实验表明的算法可有效求解带有顶点权重约束的图划分问题，且提出的改进的内点法对于大规模实例依然是可行的，且在稀疏图上表现出了良好的性能.

1 图划分问题描述

给定一个无向图G ＝（V，E），V 代表顶点集合，E代表边的集合，wij≥0为连接顶点vi，vj边的权重，其中wij＝0表示顶点vi，vj无边连接.图划分的目标即找到一个顶点子集S，使得连接两个子集S和V＼S的割边权重最小，即

引入分割向量x ∈｛－1，1｝N，若顶点vi∈S，则记xi＝1，否则，记xi＝－ 1.令W ＝［wij］，则

其中，Diag（x）表示以x ∈RN为对角元，其余元素为0的矩阵，Diag（X）表示以矩阵X ∈RN×N的对角元为元素的向量.令L ＝Diag（We）－W表示Laplacian矩阵，则问题（P）等价于如下的整数规划模型：

该文中，在已有的图模型基础上增加顶点权重约束，即在划分集合S和V＼S中，顶点vi的第j维权重和小于等于给定的上限.若每个顶点有m维权重，令第i个顶点vi的权重为［vi1，vi2，…，vim］则N个顶点的权重矩阵为Z ＝［z1，z2，…，zm］N×m，其中zj＝［v1j，v2j，…，vNj］T，j ＝1，2，…m，因此集合S中的顶点约束可表示为：

其中，U1＝［u11，u12，…，u1m］，u1j表示第j维顶点权重的上限，由此可推出：

同理，集合V＼S中的顶点约束可表示为：

其中，U2＝［u21，u22，…，u2m］，u2j表示第j维顶点权重的上限，由此可推出：

令M ＝（xT，1）T，X ＝MMT，n ＝N ＋1，因此带有顶点权重约束的图划分模型为：

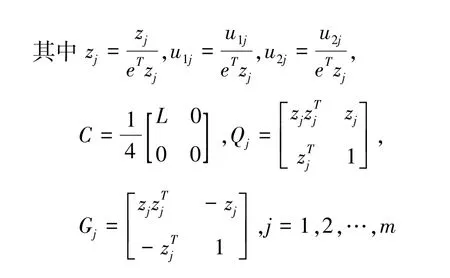
2 改进的半定规划内点法

该节中，对求解半定规划的原对偶内点法进行改进，给出了具体的初始点选取策略和步长更新策略.

令Sn 表示n × n 对称的向量空间，假设A：Mn →Rn，B：Mn →R2m为两个线性算子，且C ∈Sn，b ∈Rn，s ∈R2m，因此，第1节中带有顶点权重约束的图划分模型（SDP1）可被抽象为如下的优化问题：

利用拉格朗日方法易得到（SDP）的对偶问题为：

引入（DSDP）的对偶障碍问题为：

其中，μ ＞0为障碍参数.此障碍问题的拉格朗日函数为：

因此，（5）的一阶最优性条件为：

由log detZ和log ti的严格凹凸性可知，系统（6）存在唯一解（Xμ，yμ，tμ，Zμ）.此单参数族｛（Xμ，yμ，tμ，Zμ）：0 ≤μ ≤∞｝被称为中心路径.

2.1 初始点的选取

选取一个初始点（X，y，t，Z），原对偶内点法要求初始点满足X ＞0，Z ＞0，t ＞0 以及s－B（X）＞0.令

其中I ∈Rn×n为单位阵.若ρ ＞1.1，令X ＝I；否则，令X ＝0.5ρI，则此时X满足原问题的严格可行性，即s－B（X）＞0，X ＞0.令初始点t ＝（s－B（X））－1即满足t ＞0.在选定初始点Z ＞0时，保持其一阶最优性条件（6）成立，则有

通过上述方式找到了一个满足条件的初始点（X，y，t，Z），并由式（8）估计当前的μ 值［21］：

其中对偶间隙为gap ＝Tr（ZX）＋tT（s－B（X））.

2.2 搜索方向的推导

初始点选定后，接下来找搜索方向（ΔX，Δy，Δt，ΔZ），使得下一个迭代点（X ＋ΔX，y ＋Δy，t ＋Δt，Z ＋ΔZ）位于μ的中心路径上.为简化表示，将系统（6）重写为：

因此Fμ（ψ）＝0的解ψ*满足一阶最优性条件且是障碍问题的最优解.为找到指向ψ*的一个方向Δψ ＝（ΔX，Δy，Δt，ΔZ），使用牛顿方向法，则

因此，方向Δψ 满足：

求解该系统可得到方向（ΔX，Δy，Δt，ΔZ）.

在选定初始点Z ＞0 时，一阶最优性条件（6）成立，且由（10）（i）易得对称矩阵

然后将其代入到（10）（iv）中得到：

将（12）分别代入到（10）（ii）和（10）（iii）得到对称正定线性方程组：

2.3 选取步长的策略

在确定搜索方向之后，利用线搜索来寻找合适的步长α，关于步长α 的选取，主要基于以下考虑：

A1 步长α 要使对偶间隙gap（α）不断减小.

A2 步长α要满足X ＋αΔX ＞0，Z ＋αΔZ＞0，t ＋αΔt ＞0，以及s－B（X ＋αΔX）＞0.

为找到一个步长α满足条件A1和s－B（X ＋αΔX）＞0，t ＋αΔt ＞0，给出下面的引理.

引理2.1 令¯α为初始步长，当更新的步长α 满足

其中

时，对偶间隙gap（α）不断减小，且满足s－B（X ＋αΔX）＞0，t ＋αΔt ＞0.

证明若（14）成立，显然有s－B（X ＋αΔX）＞0，t ＋αΔt ＞0，下面只需证对偶间隙gap（α）不断减小即可.由前面的分析可知，在点（X，y，t，Z）处的对偶间隙为

则下一个迭代点（X ＋αΔX，y ＋αΔy，t ＋αΔt，Z ＋αΔZ）的对偶间隙为：

由（9），（10）（iii）和（10）（iv）可得，

又

因此有，

由（8）可得（n ＋2m）μ－gap ＜0，因此当步长α满足（15）式时，对偶间隙gap（α）不断减小.

由引理2.1 得到初始更新步长后通过线搜索寻找最终步长α，使其满足X ＋αΔX ＞0，Z－αΔZ ＞0，即满足正定性.

2.4 改进的半定规划内点算法

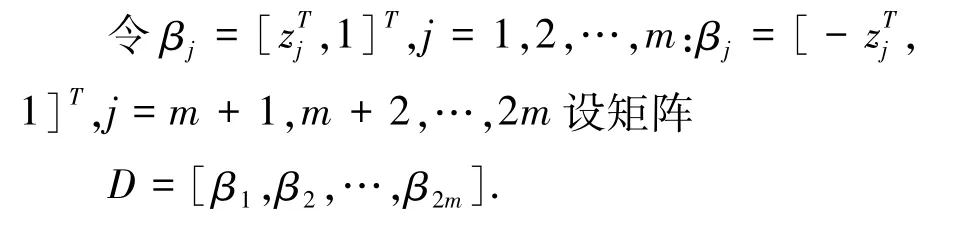
根据上面几节的分析，表1 给出求解（SDP1）改进的半定规划内点法的算法框架.

表1

3 随机超平面舍入算法

在得到了图划分模型（SDP1）的最优解X之后，基于文献［22，23］的随机超平面舍入算法来得到原问题的近似解.在此算法的基础上，将最优解X的最大特征值所对应的特征向量也作为一组解.在算法过程中增加了可行性判断，并在可行解中找到使原问题目标值最小的一组解，从而得到划分集合.利用改进的随机超平面舍入算法得到了原问题的近似解后，再应用文献［19］中的2opt启发式算法进行调整.在2opt 启发式算法中，遍历划分集合中的顶点进行交换，交换顶点的原则是在保证可行解的条件下使原问题目标函数值减小，从而得到原问题的最佳近似解.其中具体的改进的随机超平面舍入算法见表2.

表2

4 数值实验

在本节，为了测试算法的整体性能，通过数值实验和文献［19］中提出的Vc ＋2opt算法进行比较，并引入文献［19］中的两组测试集GPKCrand50和GPKCrand20 分别进行测试，其中GPKCrand50、GPKCrand20指的是非零边权占比为50%、20%的随机矩阵，边权值为区间［0，100］上的数，顶点权重为区间（0，1000］上的整数.为了避免随机性，每组实验独立运行10 次，时间取平均值.算法和文献［19］中的Vc ＋2opt算法计算得到的原问题的近似解分别记为obj1和obj2，时间记为time1和time2，单位为秒.所得实验结果见表3、表4.

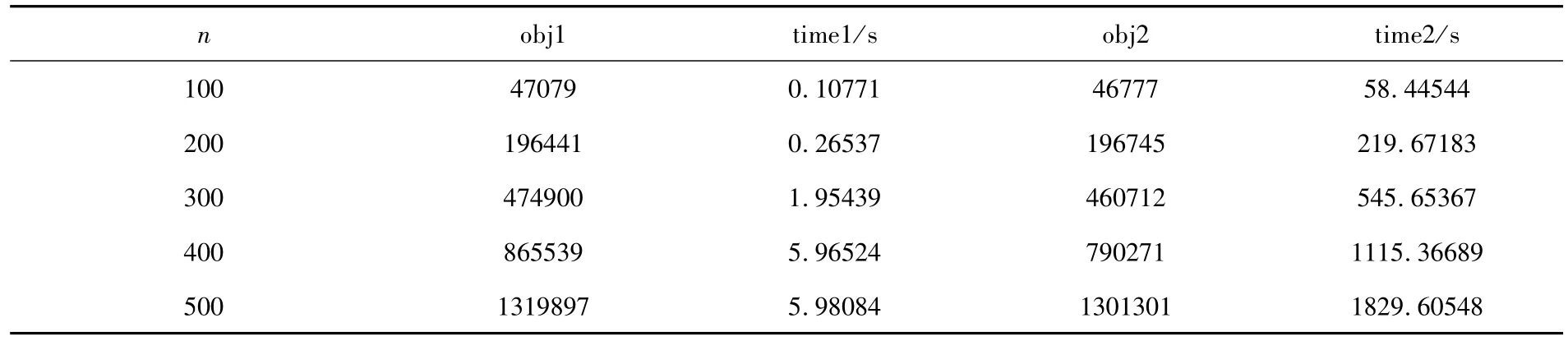
表3 在GPKCrand50上的性能比较

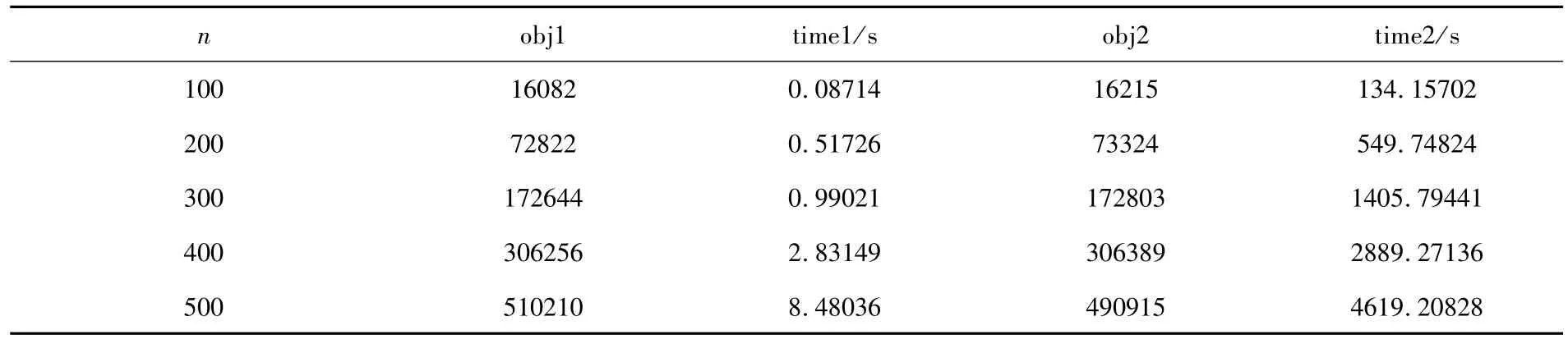
表4 在GPKCrand20上的性能比较

通过表3可以发现，在GPKCrand50图上，的算法和Vc ＋2opt算法得到的原问题的近似解没有明显的差异，但在运行时间上该文的算法明显优于Vc ＋2opt 算法.通过表4 可以发现，在GPKCrand20图上，该文的算法在原问题的近似最优解和运行时间上均表现出了很好的性能.数值实验表明该文的算法可有效求解带有顶点权重约束的图划分问题，且在稀疏图上表现出了良好的性能.

5 结论

该文将带有顶点权重的图划分问题转化为新的半定规划松弛模型，利用半定规划内点法求解该模型，并在求解过程中给出了具体的初始点选取策略和步长更新策略.随后利用改进的随机超平面舍入算法和2opt启发式算法得到原问题的近似最优解.数值实验表明该文的算法可有效求解带有顶点权重约束的图划分问题，且对于稀疏图的求解表现出了良好的性能.由于k ＝2时的图划分是k 分的基础，如何有效的递归二分得到图的k划分，有待进一步研究.