光载太赫兹信号几何成形算法比较

赵 峰,田昺瑶,王 肖,杨雄伟,赵林仙,孟 昭

(西安邮电大学 电子工程学院,陕西 西安 710121)

随着互联网技术的快速发展,各种新的服务和技术爆炸式增长,例如远程医疗、在线会议等促进了对超高速无线通信的需求[1-4]。频段范围在0.1 THz～10 THz的太赫兹波段位于微波和红外之间,集合了微波和光波的优点,在电子学和光子学领域引起了广泛的关注[5]。与微波频段相比,太赫兹波段具有丰富的带宽资源,可以解决当前系统频谱资源不足以及容量限制的问题,实现更高传输带宽和更大系统容量的通信需要[6-7]。除此之外,太赫兹波的长短不易衍射,本质上比微波或毫米波更有方向性,为太赫兹通信的抗干扰性提供了保障。同时,太赫兹通信在大雾、多尘等大气条件下衰减更低,表现相对稳定。这些特性都表明了太赫兹波通信领域具备许多明显的技术优势[8-9]。但是,电子器件因其带宽瓶颈,在电域中生成太赫兹波依旧是一个难题,借助光子辅助技术可以克服电子瓶颈的限制,实现太赫兹波宽带信号的产生[10]。

目前,国内外对于太赫兹通信方面的研究取得了诸多成果。2019年,日本研究者首次在720 GHz的载波频率下使用基于光电二极管的发射机和肖特基二极管混频器接收机验证了大于12.5 Gbit·s-1的传输速率[11]。2022年,Zhang等[12]实验演示了首个光纤-太赫兹-光纤实时传输系统,在360 GHz～430 GHz下的传输速率为125.516 Gbit·s-1,实现了103.125 Gbit·s-1数据速率的DP-QPSK在20 km标准单模光纤(Standard Single Mode Fiber,SSMF)和60 cm无线距离上的成功传输。研究成果表明,具有光子辅助的太赫兹信号传输系统可以有效提高系统传输容量。随着太赫兹技术在通信领域的不断突破和快速发展,其将成为通信系统重要的组成部分[13]。

自信息论出现以来,缩小系统容量与香农极限之间的差距成为通信领域的一个焦点。几何成形(Geometric Shaping,GS)技术作为调制格式优化技术的典型,通过调整星座点的几何位置分布,从而使系统传输速率更接近香农极限[14-19]。近年来,众多的专家学者在GS技术上进行了深入的研究。文献[20]提出了一种改进的n维星座的成对优化(Pairwise Optimization,PO)算法,并利用该算法对二维和四维的8QAM信号进行优化,验证了该算法的有效性[20]。2020年,一种低复杂度的GS-16QAM被提出,通过仿真证明,所提出的GS-16QAM在互信息方面优于常规的16QAM和现有的GS-16QAM[21]。研究表明,GS技术结合高频谱效率的QAM调制格式能够提高系统的传输性能[22-24]。因此,为了进一步提升系统的频谱效率和传输性能,将GS算法应用于QAM调制格式,结合光子辅助毫米波或太赫兹通信系统展开研究。

针对以上研究,基于广义PO算法和低复杂度(Low Complexity,LC)算法分别对8QAM、16QAM和32QAM进行GS优化,分析比较了高斯信道下GS优化后信号的互信息(Mutual Information,MI)增量。基于一种光载波抑制(Optical Carrier Suppression,OCS)和单边带调制(Single Side Band,SSB)联合矢量太赫兹信号生成方案[25],该方案无需光滤波器滤除不需要的光学边带,且SSB调制可以有效克服光纤中的走离效应,再结合上述两种GS算法进行仿真实验,进一步对系统传输性能的优化提升进行了对比分析。

1 理论分析

1.1 太赫兹信号的产生

基于OCS和SSB联合矢量太赫兹信号的产生原理如图1所示。

图1 基于OCS和SSB调制的太赫兹信号产生原理

调整单驱动强度调制器1(Intensity Modulation,IM1)的直流电偏置,实现OCS调制,产生两个边带。在基带调制阶段,由一定长度的伪随机序列(Pseudorandom Binary Sequence,PRBS)作为待发送的信息,用M-QAM格式调制,通过低通滤波器后,在下边带(Lower Side Band,LSB)-fs2处产生单边带基带信号,作为IM2的驱动信号。在IM2输出时,产生两个LSB信号,最后将调制后的LSB信号经过光电探测器(Photodetector,PD)拍频,产生矢量太赫兹信号[25]。

外腔激光器(External Cavity Laser,ECL)发出一个中心频率为fc、振幅为E0的连续光波(Continuous Lightwave,CW),其电场强度的表达式为[25]

Ein1=E0ej2πfct

(1)

式中:j表示虚数单位;t表示激光器输出的不同时刻。

用一个频率为fs1的余弦射频信号作为IM1的驱动,可以表示为

vs1(t)=VRF1cos(2πfs1t)

(2)

式中,VRF1为IM1上的射频驱动电压。假设IM1的两个Y分支具有3 dB的理想特性,则IM1的输出光场为

(3)

式中:VDC1为直流偏置电压;Vπ1为IM1的半波电压。令β1=π(VRF1/Vπ1)、γ1=π(VDC1/Vπ1),当IM1在其最小传输点偏置时,中心光载波和偶阶子载波被抑制,在IM1的输出处只有奇阶子载波,则所需的2n-1阶子载波可以表示为

Eout1(t)=E0ej2πfct·

(4)

在小信号调制下,β≪1,可忽略高阶贝塞尔函数的值,则Eout1(t)可近似为

Eout1(t)≈-E0J1(β1)[ej2π(fc+fs1)t+ej2π(fc-fs1)t]

(5)

因此,经过OCS调制后,中心载波fc被抑制,主要有两个一阶载波分别位于fc+fs1和fc-fs1,其间距为2fs1。

随后光信号入射到IM2。IM2是推挽强度调制器,其两臂由两个振幅相同、相位差一定的射频信号驱动,两个射频信号可分别表示为

vs21(t)=VRF2A2cos(2πfs2t+φ2)

(6)

vs22(t)=VRF2A2cos(2πfs2t+φ2+Δφ)

(7)

式中:VRF2为IM2上的射频驱动电压;φ2和A2分别表示基带射频信号在fs2处的相位和振幅;Δφ为信号实部与虚部之间的相位差,即Δφ=-π/2。

假设IM2的两个Y分支具有3 dB的理想特征,φ1=πVDC21/Vπ2和φ2=πVDC22/Vπ2分别是信号在IM2上臂和下臂传播引起的固定相移;VDC21和VDC22分别为IM2上、下臂的直流偏置电压。当Δφ=(2k+1)π/2、Δφ=±π/2且k为整数时,IM2在SSB模式下工作。经过fs2信号调制后,在IM2的输出处,Eout2(t)可以表示为

(8)

在小信号调制下,β≪1,可忽略高阶贝塞尔函数的值,则Eout2(t)可近似为

(9)

将式(5)代入式(9),可以得到

(10)

根据PD的平方检测律,两路光拍频,PD产生的输出光电流可表示为

(11)

其中,

G=J0(β2A2)J1(β2A2)

从式(11)可以看出,2fs1+fs2,2fs1-fs2频率处的信号同时具有相位和振幅信息,可以用来传输多进制QAM格式的信息。

1.2 几何成形

几何成形通过给定信噪比利用优化目标对等概率符号的星座点进行重新分配,使得星座点之间的最小欧式距离尽可能的大,从而获得成形增益,采用几何成形可以有效提高系统的传输性能。

1.2.1 广义成对优化算法

广义成对优化算法是在PO算法的基础上,将最小化符号错误率(Symbol Error Ratio,SER)和找到最佳的比特映射合并为在给定位映射和信噪比的情况下的最小化误码率(Bit Eerror Ratio,BER)[20]。

假设一个具有M个等概率符号的二维星座{s1,s2,…,sM},其比特映射用αi表示,i∈{1,2,…,M}。该星座中一对符号(si,sj)的SER上界可表示为

其中,

(12)

取M中任意一对星座符号,通过上述两个限制条件得到的相关约束可以分别表示为

si=-b-sj

(13)

(14)

其中,

因此,目标函数式(12)最小化可以简化为寻找sj以-b/2为中心的超球面,其半径由式(14)右边的平方根给出。式(13)定义了si和sj之间的关系,式(14)将sj的空间维度从N缩小到了N-1。

1.2.2 低复杂度算法

欧几里德距离和功率之间的权衡是几何星座成形的优化标准之一。在调制阶数不变的情况下,在坐标原点固定一个星座点,以此点为中心寻找其他星座点,可以使星座的平均能量尽可能小[21]。针对M进制的二维星座,该算法的步骤如下。

步骤2以原点为中心,将k1(1≤k1≤M)个星座点以相等的参数分布在归一化半径为r1(0≤r1≤R)的圆上。将θ1定义为k1个星座点和正实轴之间的最小角度,那么星座点集S1可以表示为

步骤3以此类推,以原点为中心,直至kn=M-(k1+…+kn-1)个星座点以相等的参数分布在归一化半径为rn=R的圆上。将θn定义为kn个星座点与正实轴之间的最小角度,则星座点集Sn可表示为

步骤4计算对应于星座点集S(S0,S1,…,Sn)的平均能量P和最小欧几里德距离D。寻找r1,…,n-1和θ1,…,n的值,按大小对计算的D和P进行排序。

步骤5当D值最大,P值最小时,可以得到优化的归一化星座点集S′。

2 仿真结果及分析

2.1 高斯信道中几何成形性能

互信息(Mutual Information,MI)是评估非均匀调制的星座成形增益的重要参数,其代表了信息在信道中传输的实际信息率。因此,可以用MI评判GS对信道容量的提升。通过仿真,分别实现广义PO算法、LC算法对星型8QAM、16QAM和32QAM信号的GS优化,并在高斯信道下研究了8QAM/GS-8QAM、16QAM/GS-16QAM及32QAM/GS-32QAM的互信息增量。

几何成形前后的信号星座图如图2所示。图2(a)、图2(b)和图2(c)分别为8QAM、16QAM和32QAM信号经过广义PO算法GS优化前后的星座图,图2(d)、图2(e)和图2(f)分别为8QAM、16QAM和32QAM信号经过LC算法GS优化前后的星座图。图中星型标记为初始星座点,菱形标记为经GS优化后的星座点。

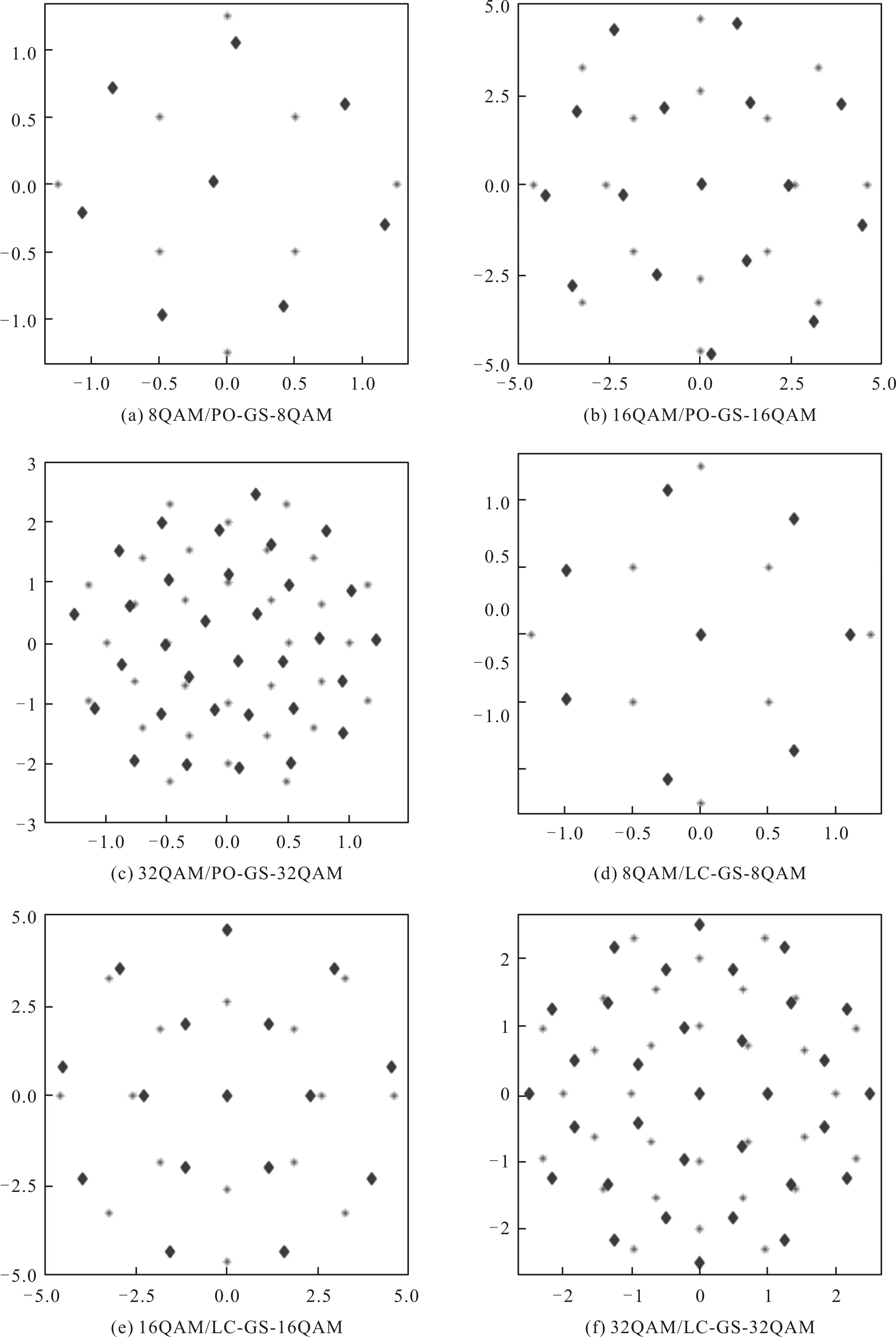
图2 几何成形前后信号的星座图

由图2可以看出,经过GS优化的信号相邻星座点之间的最小欧式距离增大,且LC算法优化的信号相邻星座点的分布较为均匀。

高斯信道中信号几何成形前后的MI仿真结果如图3所示。由图3可以看出:在图3(a)中,当MI为2.8时,PO-GS-8QAM相较于初始星座约有0.4 dB的信噪比(Signal to Noise Ratio,SNR)增益,LC-GS-8QAM相较于初始星座获得约0.5 dB的SNR增益;在图3(b)中,当MI为3.9时,PO-GS-16QAM与初始星座的SNR增益大约在1.0 dB,LC-GS-16QAM与初始星座的SNR增益大约在1.1 dB;在图3(c)中,MI为4.4时,PO-GS-32QAM和LC-GS-32QAM相较于初始星座均约有0.4 dB的SNR增益。

图3 高斯信道下几何成形前后信号的互信息

从仿真结果可以得出,在一定的SNR范围内,经过GS优化后的信号表现出比成形前的信号更好的MI性能。利用GS技术优化后,提高了信道容量,实现了更接近于香农极限的高性能传输。同时,LC算法无需使用复杂的迭代算法获得成形增益,其算法复杂度和MI增量方面均优于广义PO算法。

2.2 光载太赫兹信号几何成形性能

基于几何成形的多波段矢量太赫兹信号生成系统如图4所示。

图4 基于几何成形的多波段矢量太赫兹信号生成系统

在实验中,ECL发出一段连续光波,频率为13.8 GHz的余弦信号经过6次倍频器后展宽为82.8 GHz的射频信号驱动于直流偏置在最小工作点的IM1上。经过OCS调制后,主载波被抑制,产生频率间隔为165.6 GHz的两个主要光学子载波。根据MI增益选取成形前后的信号,利用编程进行图4中的数字信号处理(Digital Signal Processing,DSP),产生伪随机二进制序列。采用DAC转换后,两个射频矢量信号的频率为20 GHz,相位差为-π/2,经放大驱动于工作在SSB模式下的推挽调制器,在IM2的输出端获得了两个下边带SSB QAM格式的调制信号。为了提高光信号功率,采用两个掺铒光纤放大器(Erbium Doped Fiber Amplifier,EDFA)补偿信号,调制后的信号在两个EDFA之间的标准单模光纤(SMF-28)中传输。为了方便测试,利用一个可调谐光衰减器(Variable Optical Attenuator,VOA)调整进入PD的光功率。PD拍频后,得到145.6 GHz和185.6 GHz的两个主要电矢量太赫兹信号。仿真系统关键器件参数设置如表1所示。

表1 仿真系统关键器件参数

VPI仿真中信号经过不同器件的光谱和电谱图如图5所示。图5(a)为IM1输出光谱图,其中心载波和偶数阶子载波均被抑制,产生频率间隔为165.6 GHz的两个主要奇数阶子载波;图5(b)为基带调制后产生的I路信号的频谱图;图5(c)为IM2输出光谱图,在下边带分别获得两个SSB QAM信号;图5(d)为经过PD拍频后得到的145.6 GHz和185.6 GHz两个主要太赫兹信号的频谱图。

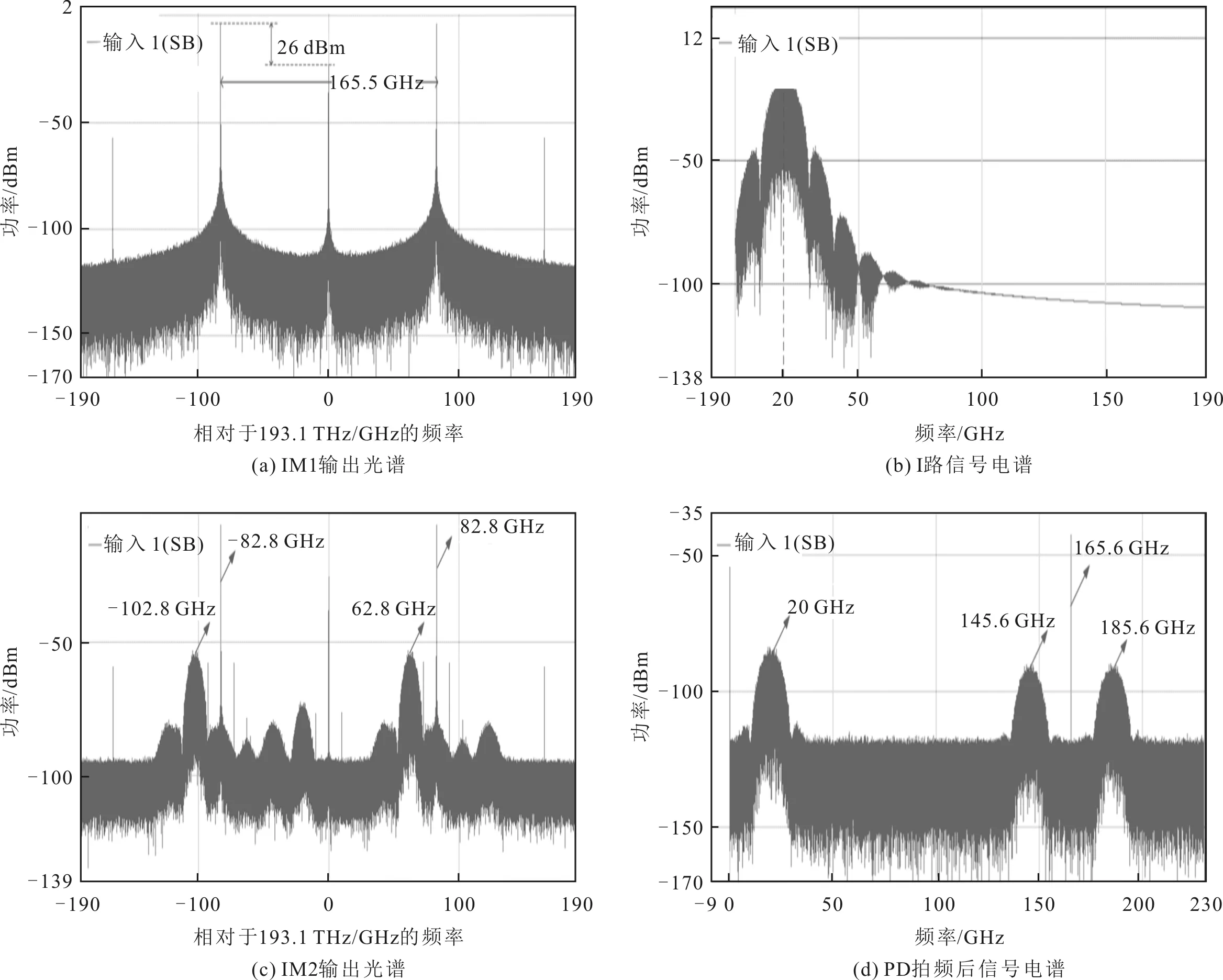
图5 VPI光谱和电谱仿真图

将系统得到的电太赫兹信号转换成离线信号,在仿真软件中对其进行离线DSP处理,从而恢复出原始数据信号。采用的DSP算法主要包括下变频、下采样、格拉姆-施密特正交归一化(Gram-Schmidt Orthogonalization Procedure,GSOP)算法、级联多模算法(Cascaded Multi Modulus Algorithm,CMMA)及针对QAM信号采用的载波恢复算法盲相位搜索算法(Blind Phase Search,BPS)。

10 Gbaud 8QAM信号误码及其星座图如图6所示,展示了145.6 GHz载频上的10 Gbaud 8QAM信号在不同调制格式下,经过BTB传输和80 km SMF传输后信号输入PD光功率与BER变化关系及其恢复信号的星座分布情况。

图6 10 Gbaud 8QAM信号误码及其星座图

由图6可以看出,图6(a)至图6(c)分别为PD输入功率为-8 dBm时,8QAM、PO-GS-8QAM及LC-GS-8QAM信号在接收端经过恢复的星座图。图6(d)中,在BTB传输条件下,PO-GS-8QAM信号在-8.14 dBm左右达到硬判决前向纠错(HD-FEC)阈值为3.8×10-3,相较于8QAM信号约有0.17 dB的增益;LC-GS-8QAM信号在-8.28 dBm左右达到该阈值,相较于8QAM信号约有0.31 dB的增益。图6(e)中,在80 km SMF传输条件下,PO-GS-8QAM信号在-7.62 dBm左右达到HD-FEC阈值,相较于8QAM信号约有0.36 dB的功率增益;LC-GS-8QAM信号在-7.71 dBm左右达到该阈值,相较于8QAM信号约有0.45 dB的功率增益。

10 Gbaud 16QAM信号误码及其星座图如图7所示, 展示了145.6 GHz载频上的10 Gbaud 16QAM信号在不同调制格式下,经过BTB传输和80 km SMF传输后,信号输入PD光功率与BER变化关系及其恢复信号的星座图。其中,图7(a)至图7(c)依次为输入PD功率为-8 dBm时DSP处理后的16QAM、PO-GS-16QAM及LC-GS-16QAM信号的星座图。图7(d)及图7(e)为不同调制格式的16QAM信号在BTB系统和经80km SMF传输后的误码率随输入PD功率的变化情况。

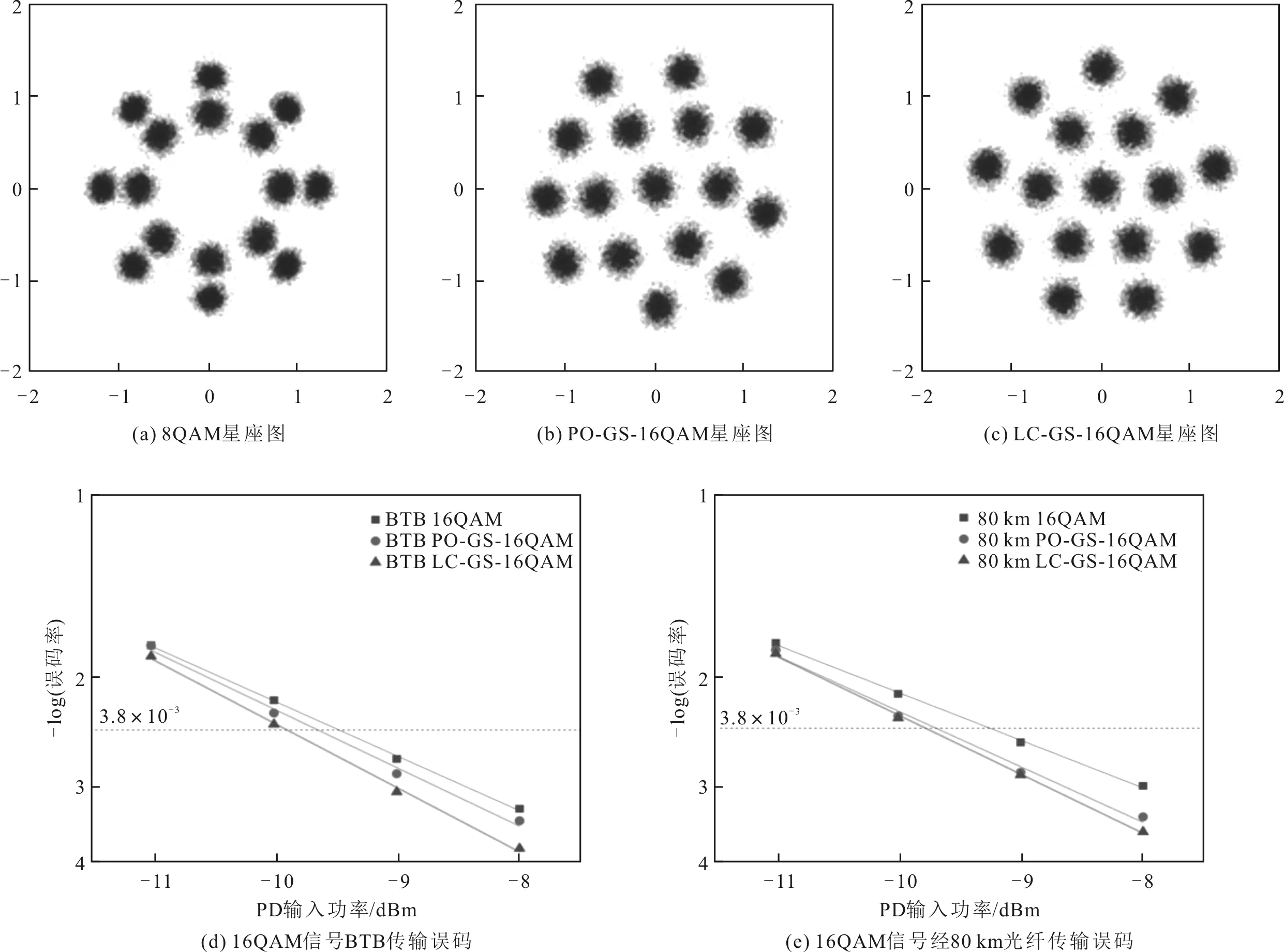
图7 10 Gbaud 16QAM信号误码及其星座图

由图7可以看出,在BTB传输系统中,误码率为3.8×10-3时,16QAM输入PD功率约为-9.47 dBm,PO-GS-16QAM输入PD功率约为-9.64 dBm,相较于16QAM约有0.17 dB的增益;LC-GS-16QAM输入PD功率约为-9.89 dBm,相较于16QAM约有0.42 dB的增益。在80 km SMF传输系统中,误码率为3.8×10-3时,16QAM输入PD功率约为-9.29 dBm,PO-GS-16QAM输入PD功率约为-9.79 dBm,相较于16QAM约有0.50 dB的增益;LC-GS-16QAM输入PD功率约为-9.82 dBm,相较于16QAM约有0.54 dB的增益。

145.6 GHz载频上的10 Gbaud 32QAM信号在不同调制格式下,经过BTB传输和80 km SMF传输后,信号误码及其星座图如图8所示。

图8 10 Gbaud 32QAM信号误码及其星座图

(续)图8 10 Gbaud 32QAM信号误码及其星座图

图8(a)至图8(c)分别为PD输入功率为-5 dBm时,32QAM、PO-GS-32QAM及LC-GS-32QAM信号在接收端经过恢复的星座图。图8(d)中,在BTB传输条件下,PO-GS-32QAM信号在输入PD功率为-6.47 dBm左右达到HD-FEC阈值3.8×10-3,相较于32QAM约有0.13 dB的增益。LC-GS-32QAM信号在-6.52 dBm左右达到该阈值,相较于32QAM信号约有0.18 dB的增益。图8(e)中,在80 km SMF传输条件下,PO-GS-32QAM信号在-3.30 dBm左右达到HD-FEC阈值,相较于32QAM信号有约0.91 dB的功率增益。LC-GS-32QAM信号在-3.65 dBm左右达到该阈值,相较于32QAM信号有约1.26 dB的功率增益。

通过以上分析,无论是在BTB还是在80 km SMF传输系统中,经GS优化后信号相较于初始信号的误码性能有一定程度提升,且LC算法优化的信号相较于广义PO算法表现出更优的误码性能。这是由于GS星座优化了星座点之间的最小欧氏距离,降低了BER,从而提升了信号的传输性能。

3 结语

基于OCS和SSB联合生成矢量太赫兹信号的传输方案,对GS优化后信号的传输性能进行对比分析。通过VPI系统仿真,分别验证了几何成形10 Gbaud 8QAM、16QAM和32QAM信号在系统中的有效传输,并对比了PO-GS-QAM和LC-GS-QAM的性能表现。验证结果表明:在加性白噪声信道中,几何成形星座的MI性能均优于初始星座,且LC算法在MI性能上的优势更明显;承载GS-QAM的145.6 GHz信号分别经BTB传输、80 km SMF传输后的BER性能均优于QAM信号,且LC-GS-QAM在实现的算法复杂度和BER性能方面更有优势。由于在仿真中器件趋于理想,实验中,器件引入了噪声和非线性的影响,信号质量将不可避免地变差。经过几何成形后的信号具有更好的抗非线性的性能,相较于传统调制格式可以有效提高系统的传输性能。