小数与整数的联系

文|陈美娟

如何建立小数与整数的关联，让学生更好地理解两者之间的联系，在教学时可以这样做。

一、画图表征，理解“一致”

1.画图：独立完成《学习单》，和同桌交流自己的想法。

2.分享：展示学生创作的不同作品，通过分析挑选出有代表性的作品（图1）。

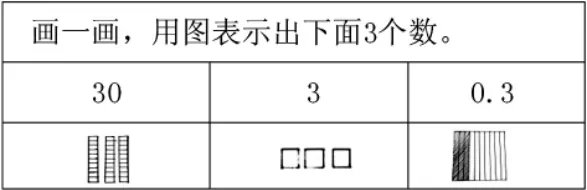
图1

3.交流：这3 种表示方法之间有什么共通之处呢？

都是画了“几个几”来表示数，也就是说，都是用计数单位的个数来表示数。画“3 个十”表示30，“3 个一”表示3，“3 个0.1”表示0.3，这里的“十”“一”“零点一”都是计数单位。

4.小结：小数和整数是一致的，都可以看成是一个或多个计数单位的连续累加，并且计数单位越多，所表示的这个数就越大。

二、实物叠加，理解“延续”

1.阅读：观察1.11 元硬币图，写出币值。

2.观察：如图2，由1.11 元开始，连续叠加硬币，说一说硬币的总币值。体会叠加到10 分，可以转化为1 角，叠加到10 个1 角，可以化为1 元。

图2

3.发现：通过分币和角币的连续叠加，我们发现，不管哪一位，满10 个就向前一位进“1”，这一点小数和整数是一样的。

4.思考：通过硬币叠加引起币值的变化的过程，想一想：小数与整数之间有什么关系？

我们发现，10 个0.1 元就是1 元，1元平均分成10 份，每份就是0.1 元。小数0.1 是整数1 平均分成10 份产生的，小数是整数的“延续”。

三、几何直观，理解“一体”

1.观察：出示（图3）数轴，看一看、想一想，你能找到哪些小数？学生独立思考，找到不同的小数并在相应位置写下来。

图3

2.迁移：把数轴延长到整数“3”（图4），你能用什么方法在这个数轴上找到与图3中不同的小数？这些小数和相邻的两个整数有什么关系？

图4

3.想象：如果把图4的数轴往右继续延长，想象一下，你还能在这个数轴上找到哪些整数？哪些小数？你能全部写完吗？

4.理解：小数和整数之间有什么关系？讨论交流后反馈学生的思考结果。

通过观察、分析、思考、想象等活动，串联“数”的知识网络，引导学生围绕小数与整数的关联建构知识体系，很好地理解小数与整数之间的联系。